THE SEISMIC PERFORMANCE OF A NEW PBL-TYPE CONNECTION IN BUCKLING-RESTRAINED BRACED REINFORCED CONCRETE FRAMES
-
摘要: 防屈曲支撑(BRB)作为一种优良的耗能构件，广泛应用于工程结构。在钢筋混凝土(RC)框架结构中布置防屈曲支撑时，支撑与梁柱节点的连接往往是结构抗震设计的重点和难点。传统的连接方式为节点板与梁柱混凝土中的预埋件焊接，再与BRB直接相连。然而，框架作用产生的开合效应和地震动引起的往复荷载容易使焊缝疲劳撕裂，从而导致节点连接破坏。为此，该文提出了开孔钢板剪力键(PBL)整体式连接节点，并将其应用于BRB-RC框架结构中。基于泛应力法，给出了节点板和PBL的设计方法。以此为基础，开展了BRB-RC框架结构的节点设计，进行了节点的有限元模拟和试验分析。研究结果表明：BRB与RC梁柱的连接节点承载力强，塑性铰转移到节点板边缘以实现损伤可控，BRB的承载-耗能性能得到了充分发挥；该新型节点连接形式安全、可靠，可显著提升结构的抗震性能。Abstract: Buckling-restrained braces (BRBs) are excellent energy-dissipating members, which are widely used in engineering structures. When BRBs are added to reinforced concrete (RC) frame structures, the connection between the beam and column joints and the BRBs usually becomes a key and difficult issue in the design. The conventional joint connection adopts welds between the gusset plate and the steel embedded parts of the concrete beams and columns, and then connects the BRB through the gusset plate. However, the opening and closing effect of the frame and the cycle loading caused by earthquakes may make the welds and joints susceptive to premature fracture. Therefore, this paper proposed a perfobond strip connector (PBL) gusset plate connection and applied it to RC frame structures. The design approach of the gusset plate and PBL connection was provided based on the generalized uniform force method. Based on this, the joint of a BRB-RC frame structure was designed, and finite element simulation and experimental analyses of the joints were carried out. The results showed that the connections in BRB-RC frames exhibited significant strength capacity, that the plastic hinge at the beam ends were transferred outside the connection region, and that the strength and energy dissipation capacity of the BRB were considerable. The proposed connection of BRBs and RC frames is effective and reliable, which significantly improves the seismic performance of the structure.
-
传统木结构各构件间的连接主要采用榫卯构造，多次震害调查结果表明 [ 1 − 2] ，榫卯节点在震后会产生不同程度的性能退化。在强震作用下榫卯发生较大变形以实现隔震耗能 [ 3 − 6] ，表现出典型的半刚性特性。研究榫卯滞回性能，对传统木结构抗震性能分析及安全评估具有重要意义。
近几十年来，许多学者就榫卯的受力机理和半刚性特性开展了试验、数值及理论研究。低周反复加载试验结果表明：榫卯具有独特的滞回特性，加载及卸载路径表现出高度的非线性 [ 7 − 11] ，滞回环具有明显的捏拢特征，可观察到节点在加卸载过程中发生典型的滑移及再加载强度退化 [ 12 − 14] ，上述滞回损伤对榫卯后续的再加载性能有显著影响。
目前，榫卯节点的数值建模方法主要包括精细化三维实体建模 [ 9, 15] 及弹簧单元简化建模 [ 16 − 17] 。前者基于精细化模型分析榫卯应力分布，明确节点破坏机理。后者通过嵌入榫卯滞回模型，可以对整体木结构开展抗震性能分析，反映榫卯对整体结构抗震性能的贡献。
但现有力学模型未考虑往复加载过程中，榫卯节点由于滞回损伤发生的加卸载路径变化，无法充分反映榫卯非线性受力特征。因此本文提出了一种改进的榫卯节点恢复力模型，考虑了榫卯滑移及再加载时的强度退化，通过直榫节点及木构架滞回试验验证了模型的准确性。开展了形状参数灵敏度分析，提出了直榫及半榫节点的参数推荐取值范围。基于现有的榫头抗弯分析方法，本文提出了模型骨架曲线控制参数的理论解，降低了其对试验测试的依赖性。
1 榫卯节点的改进滞回模型
1.1 榫卯滞回特性及现有滞回模型局限性
榫卯节点低周反复加载试验 [ 14, 18] 表明，节点塑性变形会随着加载位移的增大而逐步累积，每级位移加载对应的再加载路径会发生改变，如 图1所示。导致再加载规律发生变化的主要原因如下：① 随着加载位移增大，木构件间的缝隙增加，榫卯再加载时的滑移位移增大；② 接触面反复经历摩擦滑移，木构件表面变得光滑，滑移段的加卸载刚度降低；③ 榫头发生塑性变形，相同加载位移下节点出现再加载强度退化。
为描述榫卯节点在低周往复荷载作用下的力学行为，国内外学者提出了多种滞回模型，WU等 [ 19] 提出的通用滞回模型及ZHANG等 [ 14, 20] 提出的双线性滑移模型对于榫卯节点的捏拢特性和再加载滑移特性有较好的表征。本文以上述两种滞回模型为例，讨论现有模型的局限性。
WU等 [ 19] 所提的通用模型主要用于分析传统楼阁式木塔关键抗侧构件滞回特性，该模型采用线性段和贝塞尔曲线定义了节点的骨架曲线及加卸载路径( 图2(a))，能很好地反映榫卯在低周反复加载下的骨架曲线及卸载规律。但该模型采用的线性再加载路径，未充分考虑榫卯的滑移特性 [ 21] ( 图2(b))。
ZHANG等 [ 14] 提出的双线性滑移模型( 图3(a))，可以表征榫卯在加卸载时的摩擦滑移特性，但该模型对榫卯的骨架曲线拟合效果较差，且未考虑再加载时榫卯由于塑性变形产生的强度退化( 图3(b))。
1.2 考虑滞回损伤的榫卯改进恢复力模型定义
基于1.1节总结的榫卯滞回特性，着重考虑榫卯节点的滑移及再加载时的强度退化，提出改进后的恢复力模型。所提模型考虑了往复加载中产生的滞回损伤，定义历史最大位移 d max为损伤指标，可反映加载位移增大时，榫卯再加载滑移位移增大、滑移段加卸载刚度改变及再加载强度退化的特性。
鉴于可能存在非对称滞回曲线，模型分别定义正向和反向加载时的骨架曲线和滞回规则，相关变量采用下标“p”和“n”区分，如 图4所示。
1.2.1 骨架曲线的定义
骨架曲线的定义参考了WU等 [ 19] 的研究工作，由四个荷载位移点来描述，分别为弹性极限点 P 0 ( d 0p, f 0p) 、峰值荷载点 P 1 ( d 1p, f 1p)以及下降段的自定义点 P 2 ( d 2p, f 2p) 和 P 3 ( d 3p, f 3p)。 P 0~ P 1间的荷载位移关系使用贝塞尔曲线来描述，贝塞尔曲线任意一点 B ( d t, f t) 可通过式 (1) 求得：
B(dt,ft)=(1−t)2P0(d0p,f0p)+(2t−2t2)Pinter+t2P1(d1p,f1p), t∈[0,1] (1) 式中， P inter为以弹性刚度 k 0p过 P 0 ( d 0p, f 0p)直线与以斜率 k 1p过 P 1 ( d 1p, f 1p)直线的交点。定义骨架曲线的参数列于 表1。
表 1 骨架曲线控制参数Table 1. Model parameters governing envelopes控制参数 描述 d 0/mm 弹性极限位移 f 0/kN 弹性极限荷载 k 0/(kN/mm) 弹性刚度, k 0= d 0/ f 0 d 1/mm 峰值荷载点对应的位移 f 1/kN 峰值荷载 k 1/(kN/mm) 峰值荷载点对应的切线刚度 d 2/mm 第三点的位移 f 2/kN 对应 d 2的荷载 d 3/mm 最大位移 f 3/kN 对应最大位移的荷载 1.2.2 卸载和再加载规则
模型正反向加载时采用相同的卸载和再加载规则。在每个加载方向，使用 c 1, c 2, …, c 6, δ等7个可调参数进行定义。
捏拢点 (0, c 1p f 0p) 根据 c 1确定，卸载路径由贝塞尔曲线和指向捏拢点的直线段组成，贝塞尔曲线的初始点为 ( d pk, f pk)，切线刚度为 k unp1，贝塞尔曲线的终点和切线刚度分别为( d unp, f unp)和 k unp2。初始点的切线刚度 k unp1由 c 2p控制，如式(2)所示：
kunp1=c2pk0p (2) 卸载贝塞尔曲线的终点和切线刚度考虑两种情况( 图4)，当卸载点位移大于历史最大位移时，贝塞尔曲线的终点荷载和位移由式(3)~式(4)计算确定，切线刚度 k unp2为贝塞尔曲线终点到捏拢点 (0, c 1n f 0n) 的直线斜率，见式(5)；当卸载点位移小于历史最大位移时，贝塞尔曲线的终点位移由式(4)计算确定，终点荷载为历史最大位移下卸载直线段上该位移对应的荷载。
funp=c3pf0pdpkd0p (3) dunp=c4pdpk (4) kunp2=funp−c1nf0ndunp (5) 再加载路径由三段组成，当再加载位移 d小于滑移位移 d slip时，再加载路径为一条从捏拢点(0, c 1p f 0p)指向滑移段终点( d slip, f slip)的直线，滑移段终点由式(6)~式(7)计算得到，可用于表征榫卯的滑移特性，该直线斜率 k load1为最大历史位移对应的直线段卸载刚度 k unp2。
dslip=c5pdmax (6) {f_{{\text{slip}}}} = {c_{{\text{1p}}}}{f_{{\text{0p}}}} + {k_{{\text{load1}}}}{d_{{\text{slip}}}} (7) 当再加载位移 d大于滑移位移 d slip且小于历史最大位移 d max时，用贝塞尔曲线表征榫卯再加载时填补构件缝隙的阶段，贝塞尔曲线初始点为滑移变形的终点 ( d slip, f slip)，其切线刚度为滑移段刚度 k load1，贝塞尔曲线终点位移 d load2为历史最大位移 d max，终点荷载 f load2考虑了再加载强度退化由式(8)计算得到，终点切线刚度 k load2由式(9)计算得到。
{f_{{\text{load2}}}} = {\delta _{\text{p}}}{f_{\max }} (8) {k_{{\text{load2}}}} = {k_{{\text{0p}}}} + ({d_{\max }} - {d_{{\text{0p}}}})\frac{{({\text{1}} - {c_{{\text{6p}}}}){k_{{\text{0p}}}}}}{{{d_{{\text{0p}}}} - {d_{{\text{1p}}}}}} (9) 当再加载位移 d大于历史最大位移 d max时，再加载路径为一条从贝塞尔曲线终点( d load2, f load2)指向骨架曲线的直线，该直线斜率为贝塞尔曲线终点切线刚度 k load2。上述加卸载规则控制参数的定义列于 表2，可根据试验结果反算得到。
表 2 控制滞回形状的可调参数Table 2. Adjustable parameters governing hysteretic shapes可调参数 控制项 c 1 捏拢点荷载 c 2 卸载贝塞尔曲线初始点切线刚度 c 3 卸载贝塞尔曲线终点荷载 c 4 卸载贝塞尔曲线终点位移 c 5 再加载滑移位移 c 6 再加载刚度 δ 再加载强度 为提高抗震时程分析计算效率及收敛性，对于卸载段内的再加载情况，定义卸载段内的再加载路径为斜率较大(取为10倍的卸载初始刚度)、指向再加载路径的直线( 图4) 。对于小位移下的卸载(如抗震分析时，位移时程曲线出现原点震荡现象)，会出现贝塞尔曲线收敛困难的情况。因此，当卸载段贝塞尔曲线的初始点和终点的斜率大于初始卸载刚度时，将卸载路径简化为卸载点指向反向捏拢点的直线段( 图4)。
本文基于OpenSees开源计算平台，以上述模型为基础开发了可表征榫卯滞回特性的单轴材料模型 (UniaxialMaterial)，用于后续的模型验证。
2 榫卯改进恢复力模型的验证
2.1 直榫节点试验的拟合检验
根据ZHANG等 [ 14] 的研究，基于1/3.2直榫缩尺模型的低周反复加载试验，验证了所提恢复力模型的准确性。试验模型各构件的尺寸如 图5所示， 表3列出了试验木材的平均性能指标，指标定义见参考文献[ 14]。根据国际测试标准ISO-16670施加循环荷载，参考极限位移为65 mm，加载制度及加载方案如 图6所示。
材性指标 纵向弹性 模量 E L/MPa 弦向弹性模量 E T/MPa 径向弹性模量 E R/MPa 均值 10833.75 560.59 829.57 材性指标 顺纹抗压强度 f cL/MPa 顺纹抗拉强度 f tL/MPa 横纹抗压强度 f cR/MPa 均值 45.28 104.93 4.83 基于OpenSees平台，使用宏观弹簧单元 (Two Node Link Element) 模拟榫卯节点的滞回性能，将开发的单轴材料模型赋予宏观弹簧单元。通过拟合试验结果，得到了模型的相关参数，骨架曲线弹性极限点的转角及弯矩为 (0.019 rad, 3.57 kN·m)、 (−0.02 rad, −3.87 kN·m)，峰值荷载点的转角及弯矩为 (0.11 rad, 6.53 kN·m)、(−0.12 rad, −8.10 kN·m)，峰值荷载点对应的切线刚度为8.45 kN·m/rad、29.58 kN·m/rad，对直榫的拟合结果如 图7所示。
由于制作误差或材性差异等原因，榫卯的骨架曲线和滞回形状均表现出一定的不对称性。通过调整骨架曲线控制参数，恢复力模型骨架曲线准确地贴合了试验曲线，各级加载后峰值点对应的弯矩及割线刚度对比如 图8所示。在模型拟合时，弹性极限点取值忽略了初始小位移加载的情况，导致该阶段误差较大。模型同试验在最大位移处峰值荷载及割线刚度的误差分别为0.12%和0.39%，验证了所提模型的有效性。
通过调整滞回形状控制参数，恢复力模型能够很好地反映榫卯再加载时的滑移现象及达到历史最大位移时的强度退化现象( 图7)。由 图9可知，所提模型较为准确地模拟了直榫节点在大部分循环加载下的耗能能力，最大位移对应的单个滞回环耗能及累积耗能的误差分别为1.63%、5.76%。当加载位移较小时，榫卯非线性发展不明显，导致耗能较低，模拟时高估了该阶段的能量耗散。
同时，对滞回损伤后的直榫节点开展性能分析，总结各级位移加载后节点耗能能力的退化规律。对各级加载后的榫卯施加最大位移对应的往复荷载，无损节点、极限位移及最大位移加载后节点对应的滞回环如 图10所示，随着加载位移的增大，榫卯滑移现象愈加显著，节点最大位移对应的滞回环耗能降低。各榫卯的滞回环耗能退化如 图11所示，极限位移及最大位移加载后节点的滞回环耗能面积分别退化为无损节点的66.9%及32.9%，榫卯节点在低周反复加载下产生的损伤不可忽视，滞回损伤对榫卯节点的后续耗能能力影响较大。
榫卯木构架拟合结果对比 Comparison of fitting results of mortise and tenon timber frames 2.2 基于半榫木构架的拟合检验
为进一步验证所提恢复力模型，基于WU等 [ 22] 开展的1/2缩尺半榫木构架试验，对变幅低周反复作用下的半榫木构架滞回曲线进行了拟合。根据CUREE加载制度 [ 23] 施加荷载，参考极限位移为60 mm，初始加载为0.05Δ的等幅加载，共循环6次；之后采取主循环和次循环交替加载的方式，主循环加载的位移幅值从0.075Δ逐级增加到1.0Δ，主循环只加载1次，相应的次循环位移幅值取为主循环的75%，次循环加载次数从6次逐级减到2次；当主循环加载位移幅值达到1.0Δ时，若继续加载，则后续每一级主循环位移加载幅值增加0.5Δ，次循环加载2次，加载制度及加载方案如 图12所示。
基于Opensees建立半榫木构架数值模型如 图13所示，自定义材料骨架曲线弹性极限点的位移及荷载为 (38 mm, 3.04 kN) 、(−41.6 mm, −2.44 kN)，峰值荷载点的位移及荷载为 (150 mm, 7 kN) 、(−150 mm, −7.16 kN)，峰值荷载点对应的切线刚度为0 kN /mm、20 kN /mm，对半榫木构架的拟合结果如 图14所示。
![]()
图 14 榫卯木构架拟合结果对比Figure 14. Comparison of fitting results of mortise and tenon timber frames由于制作误差或材性差异等原因，半榫木构架的骨架曲线和滞回形状均表现出一定的不对称性。各级加载后峰值点对应的弯矩及割线刚度对比如 图15所示，模型同试验在最大位移处峰值荷载及割线刚度的误差分别为1.41%和0.91%。
通过调整形状控制参数，模型能够很好地反映榫卯木构架再加载时的滑移现象、达到历史最大位移时的强度退化现象及次循环滞回环卸载路径的变化( 图14)。由 图16可知，所提滞回模型较为准确地拟合了半榫木构架在大部分循环加载下的耗能能力，最大位移对应的单个滞回环耗能及累积耗能的误差分别为1.76%、2.69%。
2.3 模型形状参数分析及推荐取值范围
为探究各形状参数对节点滞回性能的影响，本文基于2.1节的直榫节点模型开展参数分析。基准模型参数保持一致，分别对各形状参数进行调整，在相同加载制度下，比较不同模型的耗能能力。
基于调整系数进行灵敏度分析，比较不同参数改变对滞回曲线耗能的影响。考虑到部分参数的实际物理含义，需限定其取值范围，如表征卸载曲线终点位移的参数 c 4及表征再加载强度退化的参数 δ，二者取值均需小于1。综合考虑后，选取0.9~1.1为调整系数的取值范围，对各参数进行分析。
本文基于榫卯最大位移对应的累积耗能来探究各参数对滞回曲线形状的影响规律，参数分析的结果如 图17所示，为更加清晰地对比各参数灵敏度，耗能变化百分比取为绝对值，虚线表明该参数同耗能变化呈负相关。
由 图17可知，表征再加载强度的参数 δ对榫卯耗能影响最为显著，随着强度退化，滞回环饱满程度迅速下降。其次，表征捏拢点荷载及卸载曲线终点位移的参数 c 1、 c 4对耗能较敏感，二者的折减会加剧曲线的捏缩。表征再加载滑移位移及再加载刚度的参数 c 5、 c 6同榫卯耗能呈负相关，两者的增大会使滞回曲线形状趋向Z形，导致耗能能力降低。表征卸载曲线初始点切线刚度及卸载曲线终点荷载的参数 c 2、 c 3对榫卯耗能影响较小，参数变化基本不改变滞回曲线形状。
对于直榫及半榫节点，本文基于构造特点及试验结果，给出模型形状参数的推荐取值范围。直榫节点较半榫节点构件贴合更加紧密，捏拢点荷载较高，卸载下降快，滞回曲线更加饱满。因此，直榫节点表征捏拢点荷载的参数及卸载曲线终点位移的参数 c 1、 c 4较大，同拟合结果相吻合。
在滞回损伤累积阶段，直榫节点完整性更好，加载损伤较半榫节点更为明显。因此，直榫表征再加载滑移位移、再加载刚度的参数 c 5、 c 6较大，表征再加载强度的参数 δ较小，符合试验结果。对于表征卸载曲线初始点切线刚度及卸载曲线终点荷载的参数 c 2、 c 3，直榫节点同半榫节点无明显差别，且二者对榫卯耗能影响小。
基于上述分析，直榫及半榫节点各形状参数的推荐取值范围如 表4所示。
表 4 形状参数的推荐取值范围Table 4. The recommended values for the shape parameters形状参数 直榫节点 半榫节点 c 1 0.15~0.25 0.1~0.2 c 2 15 15 c 3 0 0 c 4 0.7~0.85 0.5~0.65 c 5 0.3~0.5 0.2~0.4 c 6 0.8~0.9 1 δ 0.85~0.9 0.9~0.95 3 模型骨架曲线关键点计算方法
为降低模型对试验测试的依赖性，本文以直榫节点为例，基于CHANG等 [ 24 − 25] 、WU等 [ 26] 推导的直榫节点受力分析方法，提出改进恢复力模型骨架曲线关键点的计算方法。
对于直榫节点，不考虑材性变异及制造误差，假设其滞回性能在正负加载方向上对称。同时，假定骨架曲线不存在下降段，将峰值荷载后的骨架曲线简化为水平段。因此，为确定所提恢复力模型骨架曲线，仅需计算弹性极限点对应的转角和弯矩及峰值荷载点对应的转角、弯矩和切线刚度。
由于榫头底部应变较大，其先于榫头顶部发生受压屈服。因此，弹性极限点取榫头底部边缘刚好发生受压屈服的状态进行计算。随着节点转动角度增大，榫头逐渐进入塑性受力阶段，榫头底部及榫头顶部将先后发生屈服，通过迭代计算可以得到一系列的弯矩-转角数据，取每次迭代的切线刚度为 {k_i} = \dfrac{{{M_i} - {M_{i - 1}}}}{{{\theta _i} - {\theta _{i - 1}}}} ，定义峰值荷载点为切线刚度 {k_i} 下降为弹性点刚度5%所对应的数据点，取切线刚度 k 1=0.05 k 0。直榫转角对应的弯矩计算公式见WU等 [ 26] 的研究工作。
3.1 骨架曲线验证
基于2.1节直榫低周反复加载试验，验证理论计算方法准确性。相关计算参数根据榫卯尺寸 ( 图5) 及材性参数 ( 表3) 确定，榫头与卯眼的摩擦系数取0.5 [ 24 − 26] 。
通过计算分析，得到滞回模型骨架曲线弹性极限点的转角及弯矩为 (0.015 rad, 3.44 kN·m)，峰值荷载点的转角及弯矩为 (0.096 rad, 6.37 kN·m)，峰值荷载点对应的切线刚度为 {k_1} = 11.59 kN·m/rad，理论骨架曲线与试验结果对比如 图18所示。
![]()
图 18 理论推导与试验骨架曲线对比Figure 18. Comparison between the theoretical and experimental backbone curves总体而言，理论推导能较好地描述直榫节点的骨架曲线，峰值荷载点同试验数据吻合较好，弹性极限点弯矩略高于试验数据，其原因在于抗弯分析时未考虑剪切力的影响，高估了节点抗弯能力。
3.2 滞回性能验证
在确定模型骨架曲线后，假设模型滞回形状参数对称且不随构件尺寸发生变化，采用2.3节中直榫节点推荐参数的平均值，直榫节点的滞回曲线模拟结果如 图19所示。由于构件制作误差、木材材性差异、加载装置边界条件变化等原因，榫卯的骨架曲线和滞回形状均表现出一定的不对称性，相较反向加载正向加载段吻合较好。
![]()
图 19 直榫节点计算结果对比Figure 19. Comparison of calculation results for straight tenon joints各级加载后峰值点对应的弯矩及割线刚度对比如 图20所示，模型同试验最大位移处的峰值弯矩、割线刚度的最大误差分别为9.97%和9.46%。由 图21可知，所提滞回模型较为准确地模拟了榫卯节点在大部分循环加载下的耗能能力，最大位移对应的滞回累积耗能误差为1.6%，验证了所提模型的有效性。
4 结论
本文基于榫卯节点滞回特性，提出了一种考虑滞回损伤的榫卯恢复力模型，该模型能够很好地反映榫卯滑移特性及再加载段的强度退化。通过开展参数灵敏度分析，提出了直榫及半榫节点模型参数的推荐取值范围。同时，基于现有的榫头抗弯分析方法，提出了榫卯骨架曲线关键点参数的理论计算方法。根据分析结果，得到以下结论：
(1) 所提恢复力模型能够很好地表征直榫节点、半榫木构架滞回特性，同试验最大位移处峰值荷载、割线刚度的误差及最大位移对应的单个滞回环耗能、累积耗能的误差均小于5%。
(2) 表征再加载强度的参数δ对榫卯耗能影响最为突出，而表征卸载曲线初始点切线刚度及卸载曲线终点荷载的参数 c 2、 c 3对榫卯耗能无明显影响，参数变化基本不改变滞回曲线形状。
(3) 基于现有榫头抗弯分析方法，计算骨架曲线关键点参数理论解，能较好地描述直榫节点的骨架曲线，模型同试验最大位移处峰值弯矩、割线刚度的误差均小于10%，模拟最大位移对应的累积耗能误差为1.6%。
-
表 1 房屋结构尺寸信息
Table 1 Information of structure
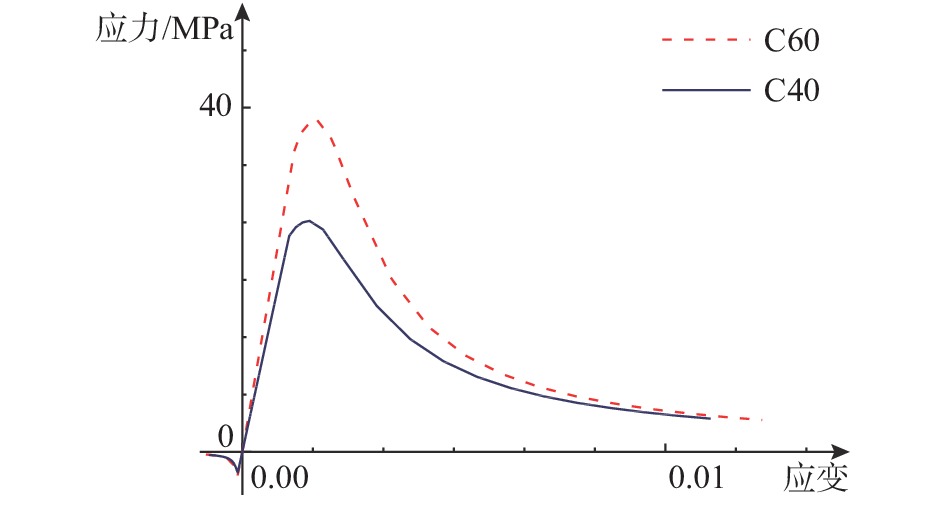
楼层 层高/m 支撑处柱/mm2 其余柱/mm2 柱混凝土 梁板混凝土 1 4.5 1100×1100 1000×1000 C60 C40 2~6 4.2 1100×1100 900×900 C60 C40 7~12 3.6 900×900 800×800 C50 C40 13~18 3.6 700×700 600×600 C50 C40 
下载: 导出CSV
表 2 BRB主要参数表
Table 2 Main parameters of BRBs
楼层 层高/m Keff/(N/mm) Ac/mm2 Fy/kN 芯材 1 4.5 1.494×106 36 172 6366.4 Q160LY 2~6 4.2 4.924×105 11 500 2024.7 Q160LY 7~12 3.6 4.203×105 9143 1609.3 Q160LY 13~18 3.6 3.293×105 7163 1261.8 Q160LY
下载: 导出CSV
-
[1] 中国防震减灾百科全书总编辑委员会. 地震工程学[M]. 北京: 地震出版社, 2014. The Editor-in-Chief Committee of the Chinese Encyclopedia of Earthquake Preparedness and Disaster Reduction. Earthquake engineering [M]. Beijing: Seismological Press, 2014. (in Chinese)
[2] 白久林, 陈辉明, 孙博豪, 等. RC框架结构地震均匀损伤优化设计[J]. 工程力学, 2020, 37(8): 179 − 188. doi: 10.6052/j.issn.1000-4750.2019.10.0572 Bai Jiulin, Chen Huiming, Sun Bohao, et al. Seismic uniform damage-targeted design of RC frame structures [J]. Engineering Mechanics, 2020, 37(8): 179 − 188. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.10.0572
[3] 杜轲, 燕登, 高嘉伟, 等. 基于FEMA P-58的RC框架结构抗震及减隔震性能评估[J]. 工程力学, 2020, 37(8): 134 − 147. doi: 10.6052/j.issn.1000-4750.2019.09.0551 Du Ke, Yan Deng, Gao Jiawei, et al. Seismic performance assessment of RC frame structures with energy dissipation and isolation devices based on FEMA P-58 [J]. Engineering Mechanics, 2020, 37(8): 134 − 147. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.09.0551
[4] 白久林, 程峰, 金双双, 潘毅, 赵俊贤. 近断层脉冲型地震作用下防屈曲支撑-钢筋混凝土框架结构的抗震性能[J]. 建筑结构学报, 2018, 39(增刊 1): 103 − 110. Bai Jiulin, Cheng Feng, Jin Shuangshuang, Pan Yi, Zhao Junxian. Seismic performance of RC frame structures with buckling-restrained brace subjected to near-fault pulse-like ground motions [J]. Journal of Building Structures, 2018, 39(Suppl 1): 103 − 110. (in Chinese)
[5] 白久林, 金双双, 欧进萍. 防屈曲支撑-钢筋混凝土框架结构基于能量平衡的抗震塑性设计[J]. 建筑结构学报, 2017, 38(1): 125 − 134. Bai Jiulin, Jin Shuangshuang, Ou Jinping. Seismic plastic design of buckling-restrained braced-RC frame structures based on energy balance [J]. Journal of Building Structures, 2017, 38(1): 125 − 134. (in Chinese)
[6] 甄伟, 邱意坤, 杨青顺, 张万开. 高层建筑中伸臂桁架的耗能性能研究[J]. 工程力学, 2021, 38(2): 36 − 43. doi: 10.6052/j.issn.1000-4750.2020.10.ST08 Zhen Wei, Qiu Yikun, Yang Qingshun, Zhang Wankai. Energy dissipation performance of outrigger in tall buildings [J]. Engineering Mechanics, 2021, 38(2): 36 − 43. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.10.ST08
[7] 吴亚杰, 宋晓滨, 蒋海燕, 顾祥林. 钢-木屈曲约束支撑增强胶合木框架抗侧性能试验研究[J]. 建筑结构学报, 2021, 42(7): 38 − 46. doi: 10.14006/j.jzjgxb.2019.0413 Wu Yajie, Song Xiaobin, Jiang Haiyan, Gu Xianglin. Experimental study on lateral performance of glulam timber frames with timber-steel buckling-restrained bracings [J]. Journal of Building Structures, 2021, 42(7): 38 − 46. (in Chinese) doi: 10.14006/j.jzjgxb.2019.0413
[8] 蒋庆, 王韶颖, 冯玉龙, 等. 底部设置BRB自复位剪力墙抗震性能和韧性试验研究[J]. 工程力学, 2021, 38(10): 173 − 180. doi: 10.6052/j.issn.1000-4750.2020.10.0725 Jiang Qing, Wang Shaoying, Feng Yulong, et al. Experimental study on aseismic performance and resilience of a self-centering shear wall with BRBs at base [J]. Engineering Mechanics, 2021, 38(10): 173 − 180. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.10.0725
[9] 谢强, 赵亮. 屈曲约束支撑的研究进展及其在结构抗震加固中的应用[J]. 地震工程与工程振动, 2006(3): 100 − 103. doi: 10.3969/j.issn.1000-1301.2006.03.028 Xie Qiang, Zhao Liang. Research on buckling-restrained brace and its applications to structural se ism ic retrofitting [J]. Earthquake Engineering and Engineering Vibration, 2006(3): 100 − 103. (in Chinese) doi: 10.3969/j.issn.1000-1301.2006.03.028
[10] 许国山, 徐小童, 王贞. 考虑防屈曲支撑影响的钢筋混凝土框架柱设计方法[J]. 建筑结构学报, 2020, 41(3): 105 − 115. Xu Guoshan, Xu Xiaotong, Wang Zhen. Design method for columns in reinforced-concrete frames with buckling-restrained braces [J]. Journal of Building Structures, 2020, 41(3): 105 − 115. (in Chinese)
[11] 刘建彬. 防屈曲支撑及防屈曲支撑钢框架设计理论研究[D]. 北京: 清华大学, 2005. Liu Jianbin. Theoretical research on the design of buckling-restrained bracing and steel frame with anti-buckling braces [D]. Beijing: Tsinghua University, 2005. (in Chinese)
[12] 曾滨, 王春林, 褚云, 许庆. 屈曲约束支撑混凝土框架节点板连接研究综述及展望[J]. 建筑结构, 2017, 47(8): 15 − 22. Zeng Bin, Wang Chunlin, Chu Yun, Xu Qing. Research review and prospect of gusset plate joint for buckling-restrained braced concrete frame [J]. Building Structure, 2017, 47(8): 15 − 22. (in Chinese)
[13] 李国强, 郭小康, 孙飞飞等. 屈曲约束支撑混凝土锚固节点力学性能试验研究[J]. 建筑结构学报, 2012, 33(3): 89 − 95. Li Guoqiang, Guo Xiaokang, Sun Feifei, et al. Experimental study of anchorage connection for buckling restrained braces [J]. Journal of Building Structures, 2012, 33(3): 89 − 95. (in Chinese)
[14] 宫海, 王彦博, 胡大柱. 混凝土框架中屈曲约束支撑新型预埋件节点研究[J]. 建筑结构, 2012, 42(11): I0032. Gong Hai, Wang Yanbo, Hu Dazhu. Research on the new embedded joints of buckling-restrained bracing in concrete frame [J]. Building Structure, 2012, 42(11): I0032. (in Chinese)
[15] 朱江, 李帼昌. 屈曲约束支撑-混凝土框架边节点受力性能分析[J]. 防灾减灾工程学报, 2017, 37(1): 134 − 139. Zhu Jiang, Li Guochang. Performance analysis of beam-column exterior joint of buckling restrained brace reinforced concrete frame [J]. Journal of Disaster Prevention and Mitigation Engineering, 2017, 37(1): 134 − 139. (in Chinese)
[16] Wu A C, Tsai K C. Hybrid tests of a full-scale two-story buckling-restrained braced RC frame [J]. Ce/papers, 2017, 1(2/3): 3139 − 3147. doi: 10.1002/cepa.366
[17] Lee Cheol-Ho. Seismic design of rib-reinforced steel moment connections based on equivalent strut model [J]. Journal of Structural Engineering, 2002, 128(9): 1121. doi: 10.1061/(ASCE)0733-9445(2002)128:9(1121)
[18] Samira Ebrahimi, Seyed Rasoul Mirghaderi, Seyed Mehdi Zahrai. Proposed design procedure for gusset plate dimensions and force distribution at its interfaces to beam and column [J]. Engineering Structures, 2019, 178: 554 − 572. doi: 10.1016/j.engstruct.2018.09.066
[19] Ishii T, Mukai T, Kitamura H, et al. Seismic retrofit for existing R/C building using energy dissipative braces [C]. Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, Canada, 2004.
[20] Fahnestock L A, Ricles J M, Sause R. Experimental evaluation of a large-scale buckling-restrained braced frame [J]. Journal of Structural Engineering, 2007, 133(9): 1205 − 1214. doi: 10.1061/(ASCE)0733-9445(2007)133:9(1205)
[21] Walters M T, Maxwell B H, Berkowitz R A. Design for improved performance of buckling-restrained braced frames [C]. Proceedings of 2004 SEAOC Convention-Monterey, Structural Engineers Association of California, Sacramento, CA, 2004: 507 − 513.
[22] Prinz G S, Coy B, Richards P W. Experimental and numerical investigation of ductile top-flange beam splices for improved buckling-restrained braced frame behavior [J]. Journal of Structural Engineering, 2014, 140(9): 04014052. doi: 10.1061/(ASCE)ST.1943-541X.0000930
[23] Berman J W, Bruneau M. Cyclic testing of a buckling restrained braced frame with unconstrained gusset connections [J]. Journal of Structural Engineering, 2009, 135(12): 1499 − 1510. doi: 10.1061/(ASCE)ST.1943-541X.0000078
[24] Qu Z, Kishiki S, Maida Y, et al. Subassemblage Cyclic Loading Tests of Buckling-Restrained Braced RC Frames with Unconstrained Gusset Connections [J]. Journal of Structural Engineering, 2015, 142(2): 04015128.
[25] Zhao J, Chen R, Wang Z, et al. Sliding corner gusset connections for improved buckling-restrained braced steel frame seismic performance: Subassemblage tests [J]. Engineering Structures, 2018, 172: 644 − 762. doi: 10.1016/j.engstruct.2018.06.031
[26] 侯和涛, 朱文灿, 曲哲, 崔士起. 屈曲约束支撑钢筋混凝土框架结构干式柔性梁柱节点的试验研究[J]. 工程力学, 2018, 35(6): 151 − 161. doi: 10.6052/j.issn.1000-4750.2017.03.0163 Hou Hetao, Zhu Wencan, Qu Zhe, Cui Shiqi. Experimental study on dry flexible beam-column joint in buckling restrained braced reinforced concrete frame structures [J]. Engineering Mechanics, 2018, 35(6): 151 − 161. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.03.0163
[27] Oguejiofor E C, Hosain M U. A parametric study of perfobond rib shear connectors [J]. Canadian Journal of Civil Engineering, 1994, 21(4): 614 − 625. doi: 10.1139/l94-063
[28] Thornton W A. On the analysis and design of bracing connections [C]. Chicago, U.S.A. Proceedings AISC National Steel Construction Conference, 1991.
[29] Muir L S. Designing compact gussets with the uniform force method [J]. Engineering Journal-American Institute of Steel Construction, 2008, 45(1): 13.
[30] American Institute of Steel Construction (AISC) [S]. Seismic provisions for structural steel buildings, Chicago, Illinois, U.S.A., 2010.
[31] JTG/T D 64-01−2015, 公路钢混组合桥梁设计与施工规范[S]. 北京: 人民交通出版, 2015. JTG/T D 64-01−2015, Code for design and construction of highway steel-concrete composite bridges [S]. Beijing: People's Communications Publishing, 2015. (in Chinese)
[32] 苏小波, 李小珍, 肖林, 等. PBL剪力键力学性能的研究现状及展望[C]// 第21届全国结构工程学术会议论文集第Ⅱ册. 北京: 中国力学学会, 2012(Ⅱ): 082 − 089. Su Xiaobo, Li Xiaozhen, Xiao Lin, et al. State-of-the-art review and trend of studies on PBL shear connector’s mechanical properties [C]// Proceedings of the 21st National Structural Engineering Conference, Volume Ⅱ. Beijing: Chinese Society of Mechanics, 2012(Ⅱ): 082 − 089. (in Chinese)
[33] 吴克川, 陶忠, 潘文, 白羽, 余文正. 不同刚度比下防屈曲支撑钢筋混凝土框架抗震性能试验研究[J/OL]. 建筑结构学报: 1 − 14 [2021-01-28]. https://doi.org/10.14006/j.jzjgxb.2020.0038. Wu Kechuan, Tao Zhong, Pan Wen, Bai Yu, Yu Wenzheng. Experimental study on seismic performance of buckling restrained braced-RC frames with different stiffness ratio [J/OL]. Journal of Building Structures: 1 − 14 [2021-01-28]. https://doi.org/10.14006/j.jzjgxb.2020.0038. (in Chinese)
[34] 赵瑛, 郭彦林. 防屈曲支撑框架设计方法研究[J]. 建筑结构, 2010, 40(1): 38 − 43, 85. Zhao Ying, Guo Yanlin. Research on design method of buckling restrained braced frames [J]. Building Structure, 2010, 40(1): 38 − 43, 85. (in Chinese)
[35] 白久林. 钢筋混凝土框架结构地震主要失效模式分析与优化[D]. 哈尔滨: 哈尔滨工业大学, 2015. Bai Jiulin. Analysis and optimization of main failure modes of reinforced concrete frame structure in earthquake [D]. Harbin : Harbin Institute of Technology, 2015. (in Chinese)
[36] Tsai K C, Tsai Z Y. Pseudo dynamic tests and analysis of a full scale two story steel buckling-restrained braced substructure under bi-directional [R]. Report No. NCREE-05-016. National Taiwan University, 2005.
[37] GB 50010−2010, 混凝土结构设计规范[S]. 北京: 中国建筑工业出版社, 2010. GB 50010−2010, Design code for concrete structures [S]. Beijing: China Building Industry Press, 2010. (in Chinese)
[38] OpenSees. Open system for earthquake engineering simulation, Version 2.4.2. Pacific Earthquake Engineering Research Center, University of California, Berkeley, 2013. http://opensees.berkeley.edu
计量
- 文章访问数: 825
- HTML全文浏览量: 396
- PDF下载量: 99
