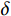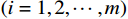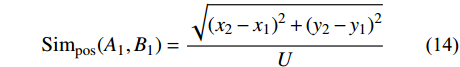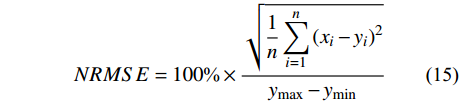NON-CONTACT IDENTIFICATION OF BRIDGE DEFLECTION BASED ON NETWORK CAMERA
-
摘要: 针对传统的桥梁挠度识别系统可达性差、效率低、不能全天候实时监测,建立了一种基于网络摄像机的桥梁挠度非接触识别系统。系统采用LED光源作为标志物,以网络摄像机作为采集设备,通过无线传输图像信息,利用计算机搭载基于HSV的快速模板匹配和基于颜色追踪(cvCamShift)的几何匹配算法获取目标的挠度时程信息,进而实现对桥梁挠度的非接触识别。通过在人行桥模型上进行四种工况的振动试验以及现场实桥测试,以此验证系统的可行性。研究结果表明:在模型试验中,系统识别得到的时域和频域信息与激光位移传感器对比的误差都小于0.6%,在雾气干扰下识别的误差仍可小于0.7%;实桥测试下,系统的识别结果与桥梁挠度仪对比的误差小于1.9%。由此表明系统鲁棒性强且经济性好,具备广泛的应用前景。Abstract: A non-contact identification system of bridge deflection based on network cameras is established to solve the problem of poor accessibility, of low efficiency, and of incompetence in all-weather real-time monitoring of the traditional bridge deflection identification system. The system used LED (light-emitting diode) lights as the marker and took network cameras as the acquisition equipment to transmit the image information wirelessly, the deflection time history information of the target is obtained by using the computer carries HSV (hue, saturation, and value) based on fast template matching and color tracking (cvCamShift) based on geometric matching algorithm, and then the non-contact identification of bridge deflection can be realized. The feasibility of the system is verified by the vibration tests under four working conditions on the footbridge model and the field test of a real bridge. The results show that: in the model test, the error of the time domain and of the frequency domain information identified by the system compared with the laser displacement sensor is less than 0.6%, and the error can still be less than 0.7% under the interference of fog. Under the real bridge test, the error of the system identification results is less than 1.9% compared with the bridge deflection instrument. This indicates that the system has strong robustness and good economy and has a wide application prospect.
-
Keywords:
- machine vision /
- real-time monitor /
- bridge deflection /
- non-contact /
- HSV
-
在近20年来,结构健康检测已经成为土木工程领域热门的研究方向,在研究和实践中获得了高度关注[1-2]。桥梁挠度是结构健康监测的重要内容之一,其反应了桥梁的受力和安全状态[3]。目前,桥梁挠度识别大致分为两类:一类为接触式测量系统;另一类为非接触式测量系统[3]。随着计算机技术及计算机视觉的快速发展,新兴的计算机视觉测量技术因其非接触、远距离和低成本的巨大优势而受到国内外广大研究人员的关注。Khuc等[4]基于常规摄像机和计算机视觉技术新开发的完全非接触式结构健康监测系统框架,通过利用成像关键点作为虚拟目标和使用改进的检测和匹配关键点算法来获取结构的挠度和振动。Shrestha等[5]研究开发了一种基于智能设备的桥梁挠度监测系统,通过图像传感器捕获图像,经实时处理以获得桥梁的特征响应挠度。Hoskere等[6]以无人机作为拍摄设备,提出一种新的基于视觉的数据提取通道,通过分治策略以无人机一次勘测结构的一部分获得结构振动的视频,从而得到全尺寸结构的模态特性。Artese等[7]利用数码相机和激光指示器,通过分析高清视频中投射在平面目标上的激光束印记的来获得桥梁任意点的位移。Lydon等[8]借助改进的运动相机和变焦镜配合特征匹配算法得到荷载下结构的精度位移变化。
以上研究成果已经推动了计算机视觉在土木邻域的发展,但计算机视觉在健康监测中的应用效率和可靠性仍然处于落后位置,对发展实时监测的研究还尚不完善。国内外研究实时监测的采集设备主要以工业相机和便携式相机为主,多数仅做了短期的实时在线监测,过程繁琐、成本高昂,而网络摄像机可解决传统系统的缺点,作为一种普及应用已久的设备,有利于让监测数据与云端相连,加快结构健康事业的发展和向社会普及结构健康监测。国内外以网络摄像机作为采集设备的系统研究还尚未有人涉足[9-10]。
桥梁挠度识别的算法随着计算机的发展而不断改进,其主要有可以全局搜索的基于数字图像相关的模板匹配[11]和适用于无人工标志物的特征点匹配[12],以及适用于高分辨率监测结构全场位移的稀疏光流[13]等。可满足网络摄像机监测条件的算法以模板匹配和几何匹配为主,但达到的精度无法进行工程实践[9,10,14]。
目前常用的模板匹配核心算法是匹配归一化互相关法(NCC),通过预先在图像中截取含有追踪目标的子图像,即模板,然后再在序列帧中做全局搜索,寻找每一个可能的位置。另外,土木工程领域的几何匹配是基于几何形状特征的模板完成目标识别和追踪。几何匹配的基本原理是对每帧图像进行边缘处理或者定位点提取,找出几何形心,通过对比各帧中几何形心的位置变化完成追踪[15]。这两种传统算法的不足是计算时间较长,环境适应差,精度低,并不适用于全天候实时计算[10,14]。
针对以上存在的问题,本文建立了一种基于网络摄像机的桥梁挠度识别系统。系统针对网络摄像机的特点搭载了两种识别算法。两种算法通过改进模板匹配和几何匹配算法克服了网络摄像机像素差、易被干扰的缺点,提高了系统监测的鲁棒性。系统通过精准安装识别在桥梁表面可以主动发光的LED光源实现对目标的跟踪识别,实时获取桥梁的挠度时程信息。
1 系统组成
系统由LED标志物、网络摄像机、计算机及系统识别算法组成,系统识别算法由通过改进的模板匹配即基于HSV的快速模板匹配和改进的几何匹配即基于颜色追踪的几何匹配组成,通过在桥梁表面安装LED光源作为标志物,利用网络摄像机实时无线传输画面进入计算机,进而利用系统识别算法获取分析桥梁挠度时程信息,系统示意图如图1所示。
1.1 标志物
目前,常见的计算机视觉识别标志物类型有平面板带规则图案[16]、平面板带不规则图案[17]、自然标志[18]、人工光源等[19-20],其中人工光源表现出来的抗干扰能力显著优于其它标志物,适合长期实时监测。故本文采用了主动发光的LED圆形红色光源,其具备较长的波长,空气穿透能力明显,能消除光线变化带来的部分影响,配合本文系统识别算法可达到最优的监测效果。
1.2 网络摄像机
网络摄像机是集成了音视频采集、网络传输、移动侦测报警等多功能于一体的数字监控产品,其网络连接方式有两种:一种为有线网络连接,通过网线或交换机与计算机连接;另一种为无线网络连接,通过无线点对点或无线交换机与计算机连接。为简化系统,本文采用无线网络连接的方式。目前,常见的是民用网络摄像机,像素普遍较低,支持低倍光学变焦和自动对焦,最大可视距离集中在30 m内,少数可搭载变焦镜头。为应对复杂工况,本文系统所用网络摄像机采用了可搭载高倍变焦镜头的网络摄像机。
1.3 系统识别算法
本文针对网络摄像机开发了两种系统识别算法,分别是基于HSV的快速模板匹配(HSV—色调(Hue)、饱和度(Saturation)、亮度值(Value)和基于颜色追踪的几何匹配,配合LED光源可进行长期实时监测。两种算法的优势不同,前者适合远程识别监测,后者更擅长近距离识别监测,系统可根据实际监测需求选择合适的算法。
系统为应对室外不可避免的风振和空气扰流,可通过机械稳定、光学稳定、数字稳定的方式减小影响,其中前两种为外在可控因素,系统通过数字稳定对采集视频进行预处理,包括运动估计、滤波平滑以及图像合成。利用特征点匹配和亚像素互相关技术消除摄像机的随机抖动带来的运动噪声[21]。
1.3.1 基于HSV的快速模板匹配
系统基于HSV的快速模板匹配不仅能够实现快速精准匹配并达到亚像素级,而且对图像灰度依赖较小,有较强的环境抗干扰能力,其算法流程如图2所示,采用基于频域的相位相关匹配算法,将图像预处理后在离线阈值颜色表中查出对应HSV阈值,再进行图像二值化,分离出追踪目标。在截取到追踪目标后定为模板,在频域里得到模板和序列帧的互功率谱,再对互功率谱做IFFT变换得到一个狄拉克函数(脉冲函数),然后寻找该狄拉克函数的峰值坐标,即可得到偏移量[22-23],主要理论如下:
将
f(x,y) 和g(x,y) 分别设定为序列帧和模板的图像信号,其中g(x,y) 是由f(x,y) 平移得到,平移距离为(dx,dy) ,即:g(x,y)=f(x−dx,y−dy) (1) 对式(1)做傅里叶变换,即:
G(u,v)=F(u,v)⋅e−2jπ(u⋅dx+v⋅dy) (2) 将变换后的式(2)左右两边同时除以
F(u,v) ,得到互功率谱H(u,v) ,即:H(u,v)=F⋅G∗|F|⋅|G∗|=e−2jπ(u⋅dx+v⋅dy) (3) 式中,
G∗ 是G 的复共轭函数,对H(u,v) 做IFF变换得到狄拉克函数δ ,该函数峰值所对应的坐标即为图像的整数级像素挠度量。为将精度提高到亚像素级,还需要做进一步的优化,系统采用相关系数曲线拟合的方式提高计算效率和精度,取出
δ 函数峰值区域局部离散相关系数矩阵(通常为(2m+1)×(2m+1) 个离散点的正方形窗口,系统采用3×3 的矩阵),利用最小二乘法拟合相关曲线逼近真实值[24-25],如图3所示,其原理如下:u(i,j)=a0+a1x+a2y,v(i,j)=b0+b1x+b2y (4) 式中:
i,j=−m:m 为窗口局部坐标;u(i,j) 和v(i,j) 为坐标(i,j) 处的原始位移;ai=0,1,2,bi=0,1,2 为未知多项式系数,等式(4)可改写成矩阵形式,即:[1−m−m1−m+1−m⋮⋮⋮100⋮⋮⋮1m−1m1mm](a0a1a2)={u(−m,−m)u(−m+1,−m)⋮u(0,0)⋮u(m−1,m)u(m,m)}=f(x,ω) (5) 式中,
ω=[ω1,ω2,⋯,ωn]T 为待定参数,寻找函数f(x,ω) 的参数ω 的最优估计值,对于求出的m组(通常m>n)坐标数据(xi,yi) (i=1,2,⋯,m) ,求解目标函数[26],即:min (6) 式中:
f(x) 为拟合后的亚像素峰值坐标;{L_i}(x)(i = 1,2, \cdots ,m) 为x 的线性函数;{\omega _i}(i = 1,2, \cdots ,n) 为最小值参数。根据曲线拟合得到的亚像素坐标({x_{{\rm{sub}}}},{y_{{\rm{sub}}}}) 与模板上目标的起始坐标({x_0},{y_0}) 进行比较,得到亚像素挠度,要求出桥梁实际挠度还需进行尺度转换。由于本文桥梁挠度只关心竖向相对挠度即一维挠度,因此这里只列出竖向相对挠度的计算算法,当相机的光轴与桥梁平面法线夹角为\theta 时,采用公式如下[27]:\Delta y = {y_{{\rm{sub}}}} - {y_0} (7) 根据尺度转换因子CF(Conversion Factor)换算成实际桥梁物理坐标,即:
CF=\frac{{d}_{{\rm{mm}}}}{{d}_{{\rm{pixel}}}\cdot {\mathrm{cos}}^{2}(\theta )}{\text{或者}}CF=\frac{D}{f\cdot {\mathrm{cos}}^{2}(\theta )}{d}_{{\rm{pixel}}} (8) \Delta {y_{{\rm{mm}}}} = \Delta y \cdot CF\;\;\;\qquad\qquad\qquad\qquad\qquad\qquad (9) 式中:D为相机到桥梁平面的距离;f为镜头焦距;CF为模板竖向物理尺寸即标志物的圆直径
{d_{{\rm{mm}}}} 与其在图像上相应像素尺寸{d_{{\rm{pixel}}}} 之比;亚像素挠度\Delta y 乘以CF即可得到实际桥梁物理竖向挠度\Delta {y_{{\rm{mm}}}} 。1.3.2 基于颜色追踪的几何匹配
本文改进的基于颜色追踪的几何匹配,其算法流程如图4所示,不仅能够缩小搜索范围,实现快速精准识别目标,且对尺度变换、非均匀光照变化、边缘软化都不敏感,可以有效应对遮挡,具备一定的抗干扰能力。其采用离线HSV图像获取在不同工况下的目标颜色阈值分割颜色表,将序列帧按梯度信息进行灰度处理,对起始图像四个边角各取4个点计算灰度平均值,在离线阈值分割颜色表中查出对应的HSV的阈值后将图像二值化处理。在二值图像中将目标颜色设定为cvCamShift追踪的目标,并通过ROI画出目标区域。将识别出的目标区域进行阈值处理、开运算(腐蚀、膨胀)后进行边缘检测出需要匹配的形状,即把检测出的形状作为模板匹配序列帧,输出模板的中心坐标,此时输出的是整数像素,需与基于HSV的模板匹配精度优化方式相同,进行曲线拟合、尺度转换后才可得到物理挠度大小。主要理论[28-29]如下:
采用Canny函数进行对ROI区域进行边缘检测,即:
\begin{split} & norm = \\ & \left\{ \begin{aligned} & {\left| {{\rm{d}}I/{\rm{d}}x} \right| + \left| {{\rm{d}}I/{\rm{d}}y} \right|,}\qquad\quad\; {{\rm L2gradient} = {\rm false}} \\ & {\sqrt {{{({\rm{d}}I/{\rm{d}}x)}^2} + {{({\rm{d}}I/{\rm{d}}y)}^2}}, }\;\; {{\rm L2gradient} = {\rm true}} \end{aligned} \right. \end{split} (10) 式中:I为图像的梯度大小;
{\rm L2gradient} 为计算图像梯度幅度,默认值为flase,直接将两个方向导数的绝对值相加,当为true时,应使用更为精准的L2范数即两个方向的导数的平方再开方。I(i,j) = \sum\limits_{m = - \infty }^\infty {\frac{{{m^2} + {n^2} - 2{\sigma ^2}}}{{{\sigma ^4}}}{{\rm e}^{ - \tfrac{{{m^2} + {n^2}}}{{2{\sigma ^2}}}}}{I_0}(i - m,i - n)} (11) 式中:
I(i,j) 为过滤后的像素(i, j)处的图像灰度强度;{I_0}(i,j) 为过滤前像素(i, j)处的图像灰度强度;m 和n为像素(i, j)处的坐标;\sigma 为高斯标准差。然后,可以得到滤波图像后的梯度,即:
\begin{split} & {I_x} = I(i,j) - I(i,j - 1) ,\\& {I_y} = I(i,j) - I(i - 1,j) \end{split} (12) 式中:
{I_x} 和{I_y} 分别为图像在x和y上的梯度值;I(i - 1,j) 为在像素(i−1, j)处的图像灰度强度。通过x和y方向的图像梯度值可获得梯度大小,即:\Delta I(i,j) = \sqrt {I_x^2 + I_y^2} (13) 式中,
\Delta I(i,j) 为像素(i, j)处的图像梯度幅值。当截取出需要匹配的形状后,代入序列帧中进行匹配,其采用欧式距离计算位置的相似度,用
{A_1}({x_1},{y_1}) 和{B_1}({x_2},{y_2}) 表示图形A与B的质心,即:{\rm{Si}}{{\rm{m}}_{{\rm{pos}}}}({A_1},{B_1}) = \frac{{\sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} }}{U} (14) 式中,U为匹配目标质心A与B距离的最大值。除了考虑距离外,图形大小、图像形状相似度亦是重要指标。
1.4 系统操作步骤
在系统操作过程中,根据实际工程概况选择合适的监测方式,本文系统根据网络摄像机的功能和各系统识别算法的优势将目标监测距离大于30 m的项目流入通道一,小于30 m的项目流入通道二。系统利用计算机实时显示和保存数据,根据各桥梁设计规范和使用要求设定桥梁挠度阈值,一旦监测数据超过阈值会触发系统报警与网络摄像机预报警信号,系统操作步骤如图5所示。
2 模型试验与数据分析
2.1 试验设计
试验所用的模型是一座长10 m,宽1.6 m的人行桥[30]。试验器材有激光位移传感器(HG-C1030)、激振器(APS400电子激振器)、网络摄像机(JM-W5022Q)、计算机、LED光源。网络摄像机的帧率为30 Hz,实际帧率受到网络传输速度的制约,目前采用的是4 G网,现场实时传输速度在每秒5 M左右,已经满足需求。网络摄像机录制的视频为
2560 \times 1960 像素,由于实验室距离较近无需配备变焦镜头。LED光源的功率为10 W,直径为50 mm。人行桥的第一阶自振频率为4.0 Hz,为能够达到较好的试验效果,激振器输入频率为4.0 Hz,幅值为6VPP。激光位移传感器的量程为30 mm,精度为0.03 mm,采样频率与网络摄像机同步。整个试验平台如图6所示。整个试验为了更好的模拟全天候复杂情况,设定在四种工况下进行了模型试验如表1所示。图7加雾模拟展示了白天加雾以及夜间加雾的工况。
表 1 试验工况Table 1. Test conditions工况1 工况2 工况3 工况4 白天 白天-雾气 夜间 夜间-雾气 由于在实验室相机摆放位置与标志物位置处于同一水平线上,无需对相机进行标定。本文两种算法识别得到的每种工况下的挠度与HG-C1030作对比求出误差。实验误差均以归一化均方根误差计算算法来衡量,具体公式如下:
NRMSE = 100\text{%} \times \frac{{\sqrt {\dfrac{1}{n}\displaystyle\sum\limits_{i = 1}^n {{{({x_i} - {y_i})}^2}} } }}{{{y_{\max }} - {y_{\min }}}} (15) 2.2 数据分析
试验过程计算是在Intel Core i7-10710,CPU1.6 GHz和内存为16 GB的计算机上。实时计算挠度的速度不仅与算法、图像大小有关也与计算机的性能有很大的联系,试验采集视频都经系统预处理过滤。图8展示了两种系统算法二值化后在计算机中呈现的图像,可有效的过滤背景,实现复杂环境下的桥梁挠度识别。
基于网络摄像机的两种系统识别算法识别结果与HG-C1030的测量结果在四种不同的工况下形状、趋势和峰值点基本一致,由于篇幅有限仅展示了工况1和工况2的识别结果,如图9所示。通过位移相应计算得到人行桥跨中自振频率,如图9中频谱分析结果所示。试验结果对比可以看出,本文提出的两种非接触式识别算法在桥梁挠度识别上的精度较高,特别在夜间环境下,处于环境条件较好的情况,主动发光的LED圆形红色光源提高了标志物的识别度,能让摄像机机迅速捕捉目标,由此两种算法在夜间的识别精度最高。当环境加入雾气干扰后,识别精度有所下降,出现部分峰值不吻合的情况,基于颜色追踪的几何匹配,由于算法对颜色敏感,识别颜色的能力较强,受到雾气的干扰较小,但是两种算法误差都未超过0.7%,满足工程实际要求。
从图9可以得出基于网络摄像机系统识别算法与HG-C1030对比的挠度测量误差,如表2所示。基于HSV的快速模板匹配在工况3下的识别误差最小仅有0.53%,在工况2下的识别误差为0.62%。基于颜色追踪的几何匹配在工况3和工况4下的识别误差都小于0.60%,在工况2下的识别误差也仅有0.58%。从图9可以得出两种算法的结构自振频率识别结果与结构一阶自振频率4.00 Hz高度吻合,如表3所示,识别准确率都可达98%以上。
表 2 挠度测量误差对比Table 2. Deflection measurement error comparison工况 算法 基于HSV的
快速模板匹配/(%)基于颜色追踪的
几何匹配/(%)工况1 0.57 0.55 工况2 0.62 0.58 工况3 0.53 0.54 工况4 0.59 0.57 表 3 频谱分析结果Table 3. Spectrum analysis results工况 算法 基于HSV的
快速模板匹配(一阶)/Hz基于颜色追踪的
几何匹配(一阶)/Hz工况1 4.08 4.06 工况2 4.06 4.05 工况3 4.08 4.07 工况4 4.05 4.01 在保证算法精度的前提下,为了评价本文两种系统识别算法的实时性,与传统的模板匹配和几何匹配作对比,表4展示了本文两种系统识别算法于其它算法基于同台计算机的帧间平均匹配时间,可以看出两种算法匹配速度都优于传统算法且完全满足网络摄像机的实时要求。
表 4 平均匹配时间对比Table 4. Mean matching time comparison算法 平均匹配时间/ms 模板匹配 125.26 几何匹配 46.85 基于HSV的快速模板匹配 14.13 基于颜色追踪的几何匹配 19.42 3 实桥测试与数据分析
3.1 实桥测试
为验证基于网络摄像机的桥梁挠度识别系统在实际情况下的有效性,将其在兰州市金城公园玻璃人行桥进行了实桥应用,该桥是桅杆式悬索桥,桥面采用钢-玻璃组合结构,主梁与次梁为国产轻型工字钢,主次梁之间采用焊接,组成钢框架,桥面采用透明玻璃铺设,均为双层夹胶钢化玻璃,全长218 m,宽2.4 m。在桥侧面跨中位置安装目标标志物(LED圆形红色光源),距离标志物111.83 m,向下倾斜
{12.89^ \circ } 的地方稳固架设了网络摄像机和桥梁挠度仪(BJQN-V,检测距离500 m内的精度为±1 mm)如图10所示。通过本文系统识别跟踪标志物的实时动态挠度,实现了对该桥的实时挠度动态监测。测试系统算法采用行人随机行走的方式激励桥梁振动,使用网络摄像机像素大小为
2560 \times 1960 配合腾龙200 mm的长焦镜头进行结构振动视频的录制,相机架设在桥梁的边测,同时也架设了桥梁挠度仪与相机进行同步监测结构振动响应,两边帧率设定一致,架设位置空间间隔小,具有较高的匹配度,以此验证系统两种算法。3.2 数据分析
本文系统与BJQN-V是两套相互独立的系统,且现场条件下难以满足用一个触发器同时启动两套系统,因此测试过程中不好控制桥梁挠度仪与相机获取数据的同步性,视频中所获取数据仅为监测段内的一部分,导致视频识别得到的振动时程曲线与桥梁挠度仪的时程曲线之间存在一定的差异,由此增加了视觉识别的难度。在现场测试时相机和长焦镜头会不可避免的受到环境气流的干扰,频谱分析中亦有强风振动和热浪为代表的噪声频率,但考虑到风致相机振动频率相对桥梁振动频率较低,两者频率并不在同一频段,且本文算法图像预处理中已对视频进行了数字稳定,因此互相干扰的影响已被降低。基于本文两种系统识别算法对金城公园玻璃桥跨中竖向挠度的监测部分结果(时域曲线、频谱分析结果)如图11所示,基于HSV的快速模板匹配与桥梁挠度仪对比的数据误差为1.78%,基于颜色追踪的几何匹配与桥梁挠度仪对比的数据误差为1.87%。由于现场环境复杂,具有很多不确定性因素,且监测距离较远,系统误差相比于实验室对比的误差有了明显的下滑,但两种算法的识别结果在时域和频域上与桥梁挠度仪基本保持一致。由时域曲线图可以看出在测试时间段内,结构竖向挠度最大幅值在9.43 mm左右,由频谱分析结果可得出结构一阶频率为0.50 Hz,二阶频率为1.08 Hz。本文两种系统识别算法识别的一阶频率与桥梁挠度仪对比误差都小于0.5%,二阶频率与桥梁挠度仪对比误差都小于1.7%。由此说明利用本文两种系统识别算法进行桥梁挠度实时监测具有较高的识别精度,满足工程实际需求。
值得关注的是,不管是本文系统还是BJQN-V都仅对桥梁低阶频率有较高的识别精度,由于环境扰流、风振等因素导致高阶频率在频谱图中的幅值较低、能量较小。因此,不能明确高阶频率的阶次和大小。这个问题将是未来研究结构健康监测的难点和重点。
4 结论
本文基于网络摄像机建立了一种桥梁挠度非接触识别系统,其系统操作简单,计算机与识别目标、计算机与网络摄像机之间都无需布线,具有非接触识别的特点,总结如下:
(1)通过模型试验和实桥测试验证了本文系统进行桥梁挠度识别的可行性,识别精度的可靠性,环境干扰的高抗性。在未来的监测过程中,应考虑两种系统识别算法的特点和监测距离,选择合适的算法。
(2)系统以LED光源作为标志物,配合提出的两种系统识别算法,对图像进行二值处理,其中基于HSV的快速模板匹配,引入了HSV颜色分割LED光源,基于颜色追踪的几何匹配,引入颜色追踪(cvCamShift),并对图像目标区域进行锁定,缩小搜索范围,可以有效提高抗噪性和计算实时运算速度,基于HSV的快速模板匹配最快匹配速度可达70.77 fps,基于颜色追踪的几何匹配计算速度为51.49 fps,都满足网络摄像机的监测要求。
(3)通过模型试验和实桥测试得出基于HSV的快速模板匹配在计算速度和远距离识别方面优于基于颜色追踪的几何匹配;而在识别精度和抗噪性能上,基于颜色追踪的几何匹配优于基于HSV的快速模板匹配。两种算法在模型试验中的识别误差都小于0.70%,实桥测试下的识别误差也小于1.90%。
-
表 1 试验工况
Table 1 Test conditions
工况1 工况2 工况3 工况4 白天 白天-雾气 夜间 夜间-雾气 表 2 挠度测量误差对比
Table 2 Deflection measurement error comparison
工况 算法 基于HSV的
快速模板匹配/(%)基于颜色追踪的
几何匹配/(%)工况1 0.57 0.55 工况2 0.62 0.58 工况3 0.53 0.54 工况4 0.59 0.57 表 3 频谱分析结果
Table 3 Spectrum analysis results
工况 算法 基于HSV的
快速模板匹配(一阶)/Hz基于颜色追踪的
几何匹配(一阶)/Hz工况1 4.08 4.06 工况2 4.06 4.05 工况3 4.08 4.07 工况4 4.05 4.01 表 4 平均匹配时间对比
Table 4 Mean matching time comparison
算法 平均匹配时间/ms 模板匹配 125.26 几何匹配 46.85 基于HSV的快速模板匹配 14.13 基于颜色追踪的几何匹配 19.42 -
[1] 王慧, 郭晨林, 王乐, 等. 基于内积矩阵及深度学习的结构健康监测研究[J]. 工程力学, 2022, 39(2): 14 − 22. doi: 10.6052/j.issn.1000-4750.2020.12.0935 Wang Hui, Guo Chenlin, Wang Le, et al. Structural health monitoring based inner product matrix and deep learning [J]. Engineering Mechanics, 2022, 39(2): 14 − 22. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.12.0935
[2] 孙雅琼, 赵作周. 桥梁结构动应变监测的温度效应实时分离与动荷载识别[J]. 工程力学, 2019, 36(2): 186 − 194. doi: 10.6052/j.issn.1000-4750.2017.12.0954 Sun Yaqiong, Zhang Zuozhou. Real-time seperation of temperature effect on dynamic strain monitoring and moving load identification of bridge structure [J]. Engineering Mechanics, 2019, 36(2): 186 − 194. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.12.0954
[3] Zhu J, Ziyue L, Zhang C. A marker-free method for structural dynamic displacement measurement based on optical flow [J]. Structure and Infrastructure Engineering, 2020, 10(22): 1 − 13.
[4] Khuc T, Catbas N. Completely contactless structural health monitoring of real-life structures using cameras and computer vision [J]. Structural Control and Health Monitoring, 2017, 24(1): e1852. doi: 10.1002/stc.1852
[5] Shrestha A, Dang J, Nakajima K, et al. Image processing–based real‐time displacement monitoring methods using smart devices [J]. Structural Control and Health Monitoring, 2020, 27(2): 1 − 18.
[6] Hoskere V, Park J, Yoon H, et al. Vision-based modal survey of civil infrastructure using unmanned aerial vehicles [J]. Journal of Structural Engineering, 2019, 145(7): 04019062. doi: 10.1061/(ASCE)ST.1943-541X.0002321
[7] Artese S, Achilli V, Zinno R. Monitoring of bridges by a laser pointer: dynamic measurement of support rotations and elastic line displacements: methodology and first test [J]. Sensors, 2018, 18(2): 338. doi: 10.3390/s18020338
[8] Lydon D, Lydon M, Taylor S, et al. Development and field testing of a vision-based displacement system using a low cost wireless action camera [J]. Mechanical Systems and Signal Processing, 2019, 121: 343 − 358. doi: 10.1016/j.ymssp.2018.11.015
[9] 叶肖伟, 董传智. 基于计算机视觉的结构位移监测综述[J]. 中国公路学报, 2019, 32(11): 21 − 39. Ye Xiaowei, Dong Chuanzhi. Review of computer vision-based structural displacement monitoring. [J]. China Journal of Highway and Transport, 2019, 32(11): 21 − 39. (in Chinese)
[10] Dong C Z, Catbas F N. A review of computer vision–based structural health monitoring at local and global levels [J]. Structural Health Monitoring, 2021, 20(2): 692 − 743.
[11] 叶肖伟, 张小明, 倪一清, 等. 基于机器视觉技术的桥梁挠度测试算法[J]. 浙江大学学报(工学版), 2014, 48(5): 813 − 819. Ye Xiaowei, Zhang Xiaoming, Ni Yiqing, et al. Bridge deflection measurement method based on machine vision technology [J]. Journal of Zhejiang University (Engineering Science), 2014, 48(5): 813 − 819. (in Chinese)
[12] Khuc T, Catbas N. Completely contactless structural health monitoring of real-life structures using cameras and computer vision [J]. Structural Control and Health Monitoring, 2016, 24(1): e1852.
[13] 朱前坤, 陈建邦, 张琼, 等. 基于计算机视觉人行桥挠度影响线非接触式识别[J]. 工程力学, 2021, 38(8): 145 − 153. doi: 10.6052/j.issn.1000-4750.2020.08.0557 Zhu Qiankun, Chen Jianbang, Zhang Qiong, et al. A non-contact recognition for deflection influence line of footbridge based on computer vision [J]. Engineering Mechanics, 2021, 38(8): 145 − 153. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.08.0557
[14] Feng D, Feng Q. Computer vision for SHM of civil infrastructure: From dynamic response measurement to damage detection – A review [J]. Engineering Structures, 2018, 156: 105 − 117. doi: 10.1016/j.engstruct.2017.11.018
[15] Yan X, Brownjohn W. Review of machine-vision based methodologies for displacement measurement in civil structures [J]. Journal of Civil Structural Health Monitoring, 2017, 8(1): 91 − 110.
[16] Park J, Moon D, Yoon H, et al. Visual-inertial displacement sensing using data fusion of vision-based displacement with acceleration [J]. Structural Control and Health Monitoring, 2018, 25(3): 1 − 14.
[17] Feng D, Feng Q. Vision-based multipoint displacement measurement for structural health monitoring [J]. Structural Control and Health Monitoring, 2015, 23(5): 876 − 890.
[18] Khuc T, Catbas N. Computer vision-based displacement and vibration monitoring without using physical target on structures [J]. Structure and Infrastructure Engineering, 2016, 13(4): 505 − 516.
[19] Tian L, Pan B. Remote bridge deflection measurement using an advanced video deflectometer and actively illuminated LED targets [J]. Sensors, 2016, 16(9): 1344. doi: 10.3390/s16091344
[20] Charalampous E, Psimoulis A, Guillaume S, et al. Measuring sub-mm structural displacements using QDaedalus: a digital clip-on measuring system developed for total stations [J]. Applied Geomatics, 2014, 7(2): 91 − 101.
[21] Rodriguez-Padilla I, Castelle B, Marieu V, et al. A Simple and Efficient Image Stabilization Method for Coastal Monitoring Video Systems [J]. Remote Sensing, 2019, 12(1): 70. doi: 10.3390/rs12010070
[22] Dashan Z, Jie G, Xiujun L, et al. A high-speed vision-based sensor for dynamic vibration analysis using fast motion extraction algorithms [J]. Sensors, 2016, 16(4): 572. doi: 10.3390/s16040572
[23] Sasikala D, Neelaveni R. Correlation coefficient measure of mono and multimodal brain image registration using fast Walsh Hadamard transform [J]. International Journal of Engineering and Technology, 2011, 3(2): 154 − 160.
[24] Pan B, Qian K, Xie H, et al. Two-dimensional digital image correlation for in-plane displacement and strain measurement: a review [J]. Measurement Science and Technology, 2009, 20(6): 062001. doi: 10.1088/0957-0233/20/6/062001
[25] Bhowmick S, Nagarajaiah S, Lai Z. Measurement of full-field displacement time history of a vibrating continuous edge from video [J]. Mechanical Systems and Signal Processing, 2020, 144: 106847. doi: 10.1016/j.ymssp.2020.106847
[26] Rathi K, Chakraborty A. Improved moving least square-based multiple dimension decomposition (MDD) technique for structural reliability analysis [J]. International Journal of Computational Methods, 2020, 18(1): 2050024.
[27] Feng D, Feng M, Ozer E, et al. A vision-based sensor for noncontact structural displacement measurement [J]. Sensors, 2015, 15(7): 16557 − 16575. doi: 10.3390/s150716557
[28] Tian Y, Zhang J, Shanshan Y. Vision-based structural scaling factor and flexibility identification through mobile impact testing [J]. Mechanical Systems and Signal Processing, 2019, 122: 387 − 402. doi: 10.1016/j.ymssp.2018.12.029
[29] 刘泉菲, 赵彬彬, 周凯. 基于分形维数的多尺度面目标匹配对相似性度量[J]. 长沙理工大学学报(自然科学版), 2018, 15(3): 1 − 7. Liu Quanfei, Zhao Binbin, Zhou Kai. Multi-scale polygon entities matched pairs' similarity measuring based on fractal dimension [J]. Journal of Changsha University of Science & Technology (Natural Science), 2018, 15(3): 1 − 7. (in Chinese)
[30] 朱前坤, 马法荣, 张琼, 等. 行人-结构竖向动力耦合效应试验研究[J]. 建筑结构学报, 2020, 41(11): 125 − 133. Zhu Qiankun, Ma Farong, Zhang Qiong, et al. Experimental study on vertical dynamic coupling effect of pedestrian-structure [J]. Journal of Building Structures, 2020, 41(11): 125 − 133. (in Chinese)
-
期刊类型引用(11)
1. 熊琛,岑成昱,周海俊,宋神友,金文良,慕容锋,梁燕媚. 基于激光-位置传感器的简支梁桥挠度测量方法研究. 工程力学. 2025(01): 223-232 .  本站查看
本站查看
2. 王翠云,杜永峰,朱前坤. 利用计算机视觉进行全路径人行桥振动舒适度评估. 振动工程学报. 2025(01): 204-213 .  百度学术
百度学术
3. 周云,郝官旺,危俊杰,杜宗,刘畅,朱茂. 基于PS-InSAR技术的大跨度桥梁结构变形监测综述. 工程力学. 2025(04): 25-37 .  本站查看
本站查看
4. 吴智深,侯士通,黄玺,黄璜. 钢筋混凝土结构移动式精准检测技术开发. 工程力学. 2024(01): 1-16 .  本站查看
本站查看
5. 郭永刚,张美霞,王凯,刘立明,陈卫明. 基于CEEMDAN-VMD-PSO-LSTM模型的桥梁挠度预测. 安全与环境工程. 2024(03): 150-159 .  百度学术
百度学术
6. 胡明月,吴邵庆,董萼良. 基于逆有限元法的三维壁板结构变形场重构. 工程力学. 2024(06): 235-245 .  本站查看
本站查看
7. 孙良晖,张慧虹,李至华,张猛. 基于逆有限元法的船体加筋板结构位移场重构. 船舶工程. 2024(07): 50-57 .  百度学术
百度学术
8. 杜文康,雷冬,白鹏翔,朱飞鹏. 基于TM-DIC方法的桥梁动态响应测量. 计算机仿真. 2024(08): 175-181 .  百度学术
百度学术
9. 朱前坤,崔德鹏,张琼,杜永峰. 利用计算机视觉识别人行桥时变模态参数. 振动工程学报. 2023(01): 52-61 .  百度学术
百度学术
10. 朱前坤,崔德鹏,刘艺,杜永峰. 基于计算机视觉的复杂背景人行桥振动识别. 土木工程学报. 2023(06): 75-86 .  百度学术
百度学术
11. 李清泉,陈睿哲,涂伟,陈智鹏,张博琛,严爱国,殷鹏程. 基于惯性相机的大跨度桥梁线形形变实时测量方法. 武汉大学学报(信息科学版). 2023(11): 1834-1843 .  百度学术
百度学术
其他类型引用(6)




 下载:
下载: