隧道临空面形成后开挖面后方围岩失去支撑而围岩变形速率较快，因此需要采用及时施作的初期支护以控制围岩变形。锚固体系作为一种及时有效的支护手段，因其灵活性强、成本低廉且能主动控制围岩变形而得到设计者的青睐，在隧道与地下工程中得到了广泛应用^[1-4]。因此，研究锚固体系作用机理及其变形控制效果，对于隧道围岩稳定性控制及锚固体系的科学设计具有重要意义。

目前对于锚固体系作用机理的认识主要包括悬吊理论、组合梁理论、压缩拱理论以及地层加固理论^[5-8]。为了研究锚固体系的支护效果，国内外学者采用数值模拟、现场实测、室内试验和理论解析等手段进行了研究。Freeman^[9]通过对锚杆受力过程及锚杆应力分布进行现场试验，提出了全长粘结锚杆中性点的概念。郭军等^[10]通过数值模拟和现场试验方法分析了黄土隧道中系统锚杆的作用效果，指出边墙锚杆作用效果显著而拱部锚杆较弱。Zuo等^[11]采用室内拉拔试验，研究了不同直径匹配下锚固体的破坏模式，提出了保证锚固效果的杆体与钻孔直径匹配建议值。蔡跃等^[12]基于拉拔试验结果提出了锚杆与围岩相互作用分析模型，揭示了杆体与围岩接触面间的耦合作用机理。与数值分析和物理模拟相比，理论解析过程透明且使用方便，在进行锚固效果分析时更为直观，有助于识别出关键锚固参数，因此在锚固机理的分析中得到了广泛应用^[13-15]。

针对隧道锚固机理的理论解析，主要包括等效支护力和等效加固圈两种处理方式。其中等效支护力将锚杆作用考虑为作用于隧道洞壁的均布力或围岩内部体积力^[16]，本质上是锚固体系的支护作用；而等效加固圈则将锚杆作用等效为锚固区内围岩力学参数的提高^[17]，本质上是围岩层面的加固作用。此外，相关学者对于锚杆与锚索的组合支护形式也进行了研究^[18-21]，对于认识锚固体系的作用机理具有重要意义。但上述研究大多未考虑锚固体系作用过程中与围岩相对位置的变化情况，且对于锚杆与锚索支护时机相对滞后性的影响机制未见报道。

事实上，锚固体系伸入围岩内部，兼有支护与加固的双重作用，且其与围岩相互作用过程复杂，现有研究仅考虑单一作用而可操作性较差^[22]。此外，由于锚固体系施作的滞后性，且考虑到锚杆、锚索作用范围及其与围岩结构的位态关系，二者作用功能有所区别^[23]。而目前对于锚固体系在大跨隧道中的协同作用全过程机理仍不十分明确，缺乏科学合理的设计方法。

为此，本文基于开挖面空间效应，综合考虑锚固体系的等效支护力和加固圈效应，对锚杆、锚索先后施作时围岩力学状态进行分析，根据锚固构件与围岩结构空间位态关系的发展规律，建立锚固体系的变形控制机理模型，揭示了锚固作用下隧道围岩力学响应的全过程演化机制，进一步分析锚固体系对于围岩变形的控制效果及其影响因素，可为隧道支护体系协同设计提供参考。

1   分析模型与基本假设

1.1   隧道锚固体系作用分析模型

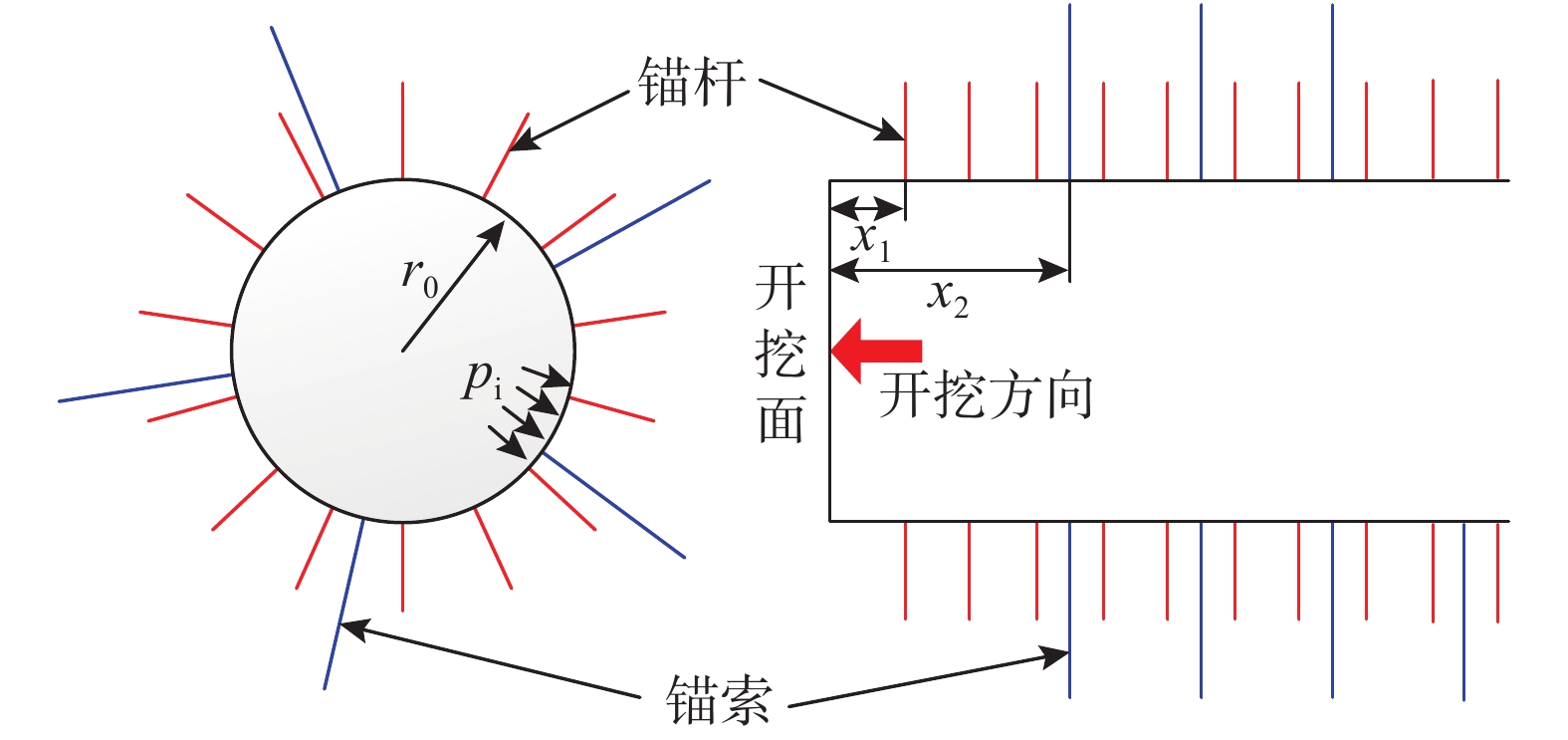
对于一深埋隧道，采用等代圆法将其等效为圆形断面^[24]。假定围岩为各向同性均匀的理想弹塑性体，无穷远处受静水应力${p_0}$作用，隧道内边界作用均匀支护反力${p_{\rm{i}}}$，隧道半径为${r_0}$，围岩屈服后在隧道洞周形成半径为${r_{\rm{p}}}$的塑性区，考虑塑性围岩的剪胀效应。考虑到锚固体系滞后于隧道开挖面施作，且锚杆支护施作更为及时，故假定锚杆、锚索施作时距开挖面距离分别为${x_1}$、${x_2}$，如图1所示。

锚固区和原岩区围岩均满足Hoek-Brown强度准则如下^[25]：

式中：${\sigma _1}$、${\sigma _3}$分别为第一主应力和第三主应力，在本章假设中分别为${\sigma _\theta }$和${\sigma _r}$；m和s分别为岩体材料常数；${\sigma _{\rm{c}}}$为完整岩石单轴抗压强度。

图  1  隧道锚固系统的布置

Figure  1.  Arrangement of tunnel anchoring system

下载: 全尺寸图片 幻灯片

1.2   隧道开挖面空间效应及其表征方式

隧道围岩弹塑性变形的释放并非瞬时完成，而是随着开挖面推进逐渐发展，因此在锚杆施作时隧道围岩已发生一定程度的变形，此即隧道开挖面空间效应^[26]。此约束效应可由虚拟支护力表征，其求解思路为^[27]：首先根据围岩特性曲线获得分析断面径向位移${u_{{r_0}}}$与支护力${p_{\rm{i}}}$关系，并得到无支护条件下围岩理论最大位移量${u_{{r_0}}}( \infty )$，再代入位移释放率$u_x^*$表达式，进而获得虚拟支护力与空间位置的关系。

关于隧道位移释放率的描述，有众多学者进行了研究，而Hoek基于Chern等^[28]的实测数据采用最佳拟合方法得到的经验公式因其表达式简单且将开挖面前后统一描述而得到广泛应用。此外，李二兵等^[29]通过现场原位试验表明，Hoek公式对于围岩全过程变形的拟合结果与实测数据较为接近，为最优求解方程，因此本文采用该公式来进行求解：

式中，$x$为分析断面距开挖面距离，$x = 0$处为开挖面，负值表示开挖面前方，正值表示开挖面后方。

1.3   锚固体系全过程作用工况

由于锚杆长度增加时其柔性特征越显著，因此实际工程中常用的锚杆长度是有限的，而对于大断面隧道围岩穿越不良地质体时塑性区范围往往较大，此时锚杆仅能作用于塑性区，其锚固效果十分有限。此外，对于高速铁路隧道往往具有高可靠性需求，则需施作锚索以提高锚固体系的整体刚度。采用钢绞线组成的锚索一般刚度较大而延伸率较小，长锚索可伸入稳定岩层从而调动围岩承载。

鉴于锚杆伸入塑性区时有必要施作锚索以保证锚固体系协同承载，因此本文主要针对锚索伸入弹性区且锚杆伸入塑性区的最终状态进行解析。根据锚杆、锚索施作时隧道围岩弹塑性状态及相互作用过程中锚杆、锚索与塑性区空间位置关系，可将锚固体系与围岩相互作用全过程分为6种工况，如图2所示。

图  2  隧道锚固体系与围岩作用全过程机理模型

Figure  2.  Mechanism model of whole process between tunnel anchorage system and surrounding rock

下载: 全尺寸图片 幻灯片

工况A，锚杆施作时围岩处于弹性状态且锚杆施作伸入弹性区，锚索施作时围岩弹性；

工况B，锚杆施作时围岩处于弹性状态，锚索施作时围岩塑性且锚杆伸入塑性区；

工况C，锚杆施作时围岩处于弹性状态，锚索施作时围岩塑性且锚杆伸入弹性区；

工况D，锚杆施作时围岩处于塑性且锚杆施作伸入弹性区，锚索施作时围岩塑性且锚杆伸入弹性区；

工况E，锚杆施作时围岩处于塑性且锚杆施作伸入弹性区，锚索施作时围岩塑性且锚杆伸入塑性区；

工况F，围岩塑性阶段锚杆施作伸入塑性区，锚索施作时围岩塑性。

2   锚固体系与围岩作用全过程解析

2.1   工况A解析

无支护条件下的隧道弹性位移可表示为：

式中，$E$和$\mu$分别为围岩弹性模量和泊松比。

将$r = {r_0}$，${p_{{i}}} = 0$代入式(3)中可得：

将$x = {x_1}$代入式(2)可得锚杆施作时围岩已释放位移量：

结合式(3)可得此时虚拟支护力为：

因此，对于$x < {x_1}$时围岩变形采用式(3)计算。当${x_1} \leqslant x < {x_2}$时仅有锚杆作用，根据Fahimifar等^[16]，锚杆的等效加固圈效应可考虑为围岩弹性模量的增加，则锚杆单一锚固区围岩弹性模量为：

若锚杆在围岩变形发生前即已施作，则围岩变形可表示为：

式中，${r_{{{\rm{sb}}}}} = {L_{{{\rm{sb}}}}} + {r_0}$，${L_{{{\rm{sb}}}}}$为锚杆长度，${p_{{r_{{\rm{{\rm{sb}}}}}}}}$为锚杆单一锚固区与原岩区径向接触力，有^[17]：

式中，$\alpha = r_{{{\rm{sb}}}}^2 - r_0^2$。

考虑到弹性区虚拟支护力与围岩参数无关，将式(6)代入式(8)并考虑式(5)可得由于锚杆施作的滞后性而产生的增量位移为：

则锚杆施作后围岩位移表达式为：

对于某一分析断面，虚拟支护力表达式为^[27]：

鉴于锚索长度大于锚杆，因此，将锚杆与锚索共同作用区域称为双重锚固区，锚索长于锚杆部分区域称为锚索单一锚固区。设隧道纵向上弹塑性交界临界距离为${x_{{\rm{cr}}}}$，当${x_1} < {x_2} < {x_{{\rm{cr}}}}$时锚索施作时围岩弹性，则锚索施作后双重锚固区弹性模量可表示为：

式中：下标b和c分别表示锚杆和锚索；${E_{\rm{s}}}$、${A_{\rm{s}}}$、${S_{\rm{c}}}$和${S_{\rm{l}}}$分别表示锚杆(索)弹性模量、截面积、间距和排距。

同理可得锚索单一锚固区围岩弹性模量为：

对于内径${r_1}$、外径${r_2}$的厚壁圆筒，当内外荷载分别为${p_1}$和${p_2}$时弹性径向变形可表示为^[30]：

考虑到锚索单一锚固区和双重锚固区及锚索单一锚固区与原岩区位移连续条件，则有：

将式(16)代入式(15)可得锚固区与原岩区界面上径向应力${p_{{r_{{\rm{sc}}}}}}$和锚索单一锚固区与双重锚固区径向接触力${p_{{r_{{\rm{sb}}}}}}$表达式为：

式中，各系数表达式如下：

根据式(10)易推知由于锚杆和锚索施作的滞后性而产生的增量位移为：

则当${x_2} < x \leqslant {x_{{\rm{cr}}}}$时围岩变形表达式为：

当$x > {x_{{\rm{cr}}}}$时围岩塑性区产生，无支护条件下隧道塑性区围岩变形表达式为^[31]：

式中：$M = \dfrac{1}{2}\sqrt {\dfrac{{{m^2}}}{{16}} + m\dfrac{{{p_0}}}{{{\sigma _{\rm{c}}}}} + s} - \dfrac{m}{8}$；$f$为剪胀系数且$f = \dfrac{{1 + \sin \psi }}{{1 - \sin \psi }}$；$\psi$为剪胀角。塑性区半径${r_{\rm{p}}}$表达式为：

式中，$N = \sqrt {m{\sigma _{\rm{c}}}{p_0} + s\sigma _{\rm{c}}^2 - Mm\sigma _{\rm{c}}^2}$。

将$r = {r_0}$代入式(22)可得虚拟支护力表达式为：

式中，$n = \exp \left[ {\dfrac{{f + 1}}{m}\left( {\dfrac{{2N}}{{{\sigma _{\rm{c}}}}} - 2\sqrt s } \right)} \right]$。

当虚拟支护力小于临界值时将发生塑性位移，该临界值为：

将式(24)与式(25)联立并结合式(5)可得隧道纵向弹塑性分界处距开挖面距离为：

考虑锚杆支护的等效支护力效应，将此作用力以附加体积力作用于围岩。当塑性区开始产生时锚杆最初伸入弹性区，此时锚固区围岩应力为^[17]：

式中，${\sigma _{{\rm{sb}}}}$、${\sigma _{\rm sc}}$分别为锚杆、锚索的径向约束力，有：

假定锚索与围岩变形协调，则有：

锚索施作时围岩径向应变${ {\bar{\varepsilon} _{{r}}} ^\prime }$表达式为：

则有：

式中：

${N_{\rm{E}}} = \left( {\dfrac{{{E_{{\rm{sb}}}}{A_{{\rm{sb}}}}}}{{{S_{{\rm{cb}}}}{S_{{\rm{lb}}}}}} + \dfrac{{{E_{{\rm{sc}}}}{A_{{\rm{sc}}}}}}{{{S_{{\rm{cc}}}}{S_{{\rm{lc}}}}}}} \right)$，${N_{\rm F}} = \left( {\dfrac{{{F_{\rm sb}}}}{{{S_{\rm cb}}{S_{\rm lb}}}} + \dfrac{{{F_{\rm sc}}}}{{{S_{\rm cc}}{S_{\rm lc}}}}} \right)$。

将式(31)代入平衡方程：

并积分可得双重锚固塑性区围岩径向应力为：

式中：${f_1}\left( {{r_0}} \right)$为与边界条件相关的待定参数；${f_1}\left( r \right)$需用数值方法求解。

隧道围岩双重锚固弹性区应力表达式为：

式中，${\sigma _{\rm{p}}}$为弹塑性界面处径向应力。考虑到弹性区有${\sigma _{ r}} + {\sigma _\theta } = 2{p_0}$，将其代入式(1)可得：

由式(17)易推得${p_{{r_{{\rm{sc}}}}}}$和${p_{{r_{{\rm{sb}}}}}}$表达式为：

式中：

考虑到弹塑性界面及隧道洞壁应力边界条件：

则联立式(33)~式(37)可得隧道塑性区半径表达式，此时隧道洞壁围岩变形表达式为：

当$x > {x^*}$时，锚杆端部位于塑性区内，此时锚索单一锚固塑性区径向应力满足：

代入式(32)并积分可得锚索单一锚固塑性区围岩径向应力表达式为：

式中：${f_2}\left( {{r_0}} \right)$为与边界条件相关的待定参数；${f_2}\left( r \right)$需用数值方法求解。

当围岩开始进入塑性时锚杆端部起初位于弹性区，随着应力释放围岩塑性区半径逐渐扩大，当锚杆端部恰位于弹塑性交界处时有${r_{\rm{p}}} = {r_{{\rm{sb}}}}$，${\sigma _{\rm{p}}} = {p_{{r_{{\rm{sb}}}}}}$。将式(35)与式(33)联立可得塑性区应力表达式，而后令$r = {r_0}$可得此时虚拟支护力${p_{{i}}} = {\sigma _{{r}}}\left| {_{r = {r_0}}} \right.$，并代入式(24)可得此时分析断面距开挖面距离${x^*}$。

双重锚固区与单一锚固区应力连续性条件为：

则联立式(33)、式(37)、式(35)、式(40)和式(41)可得隧道围岩塑性区半径，再代入式(38)并结合式(24)即可得到隧道围岩变形量沿隧道纵向的演化规律。

2.2   工况B解析

当${x_2} > {x^*} > {x_{{\rm{cr}}}}$时锚索施作时围岩处于塑性状态且锚杆伸入围岩塑性区，因此围岩变形的纵向发展规律分为五段。

1)对于$x < {x_1}$段围岩变形采用式(3)计算，而虚拟支护力表达式为：

2)对于${x_1} < x < {x_{{\rm{cr}}}}$段围岩变形采用式(11)计算，虚拟支护力采用式(42)。

3)对于${x_{{\rm{cr}}}} \leqslant x < {x^*}$段，根据前文分析可得锚杆单一锚固区内围岩径向应力满足：

锚杆施作时围岩径向应变为：

由于塑性区全部属于锚固区，将式(7)代入式(22)可得锚固塑性区围岩径向应变表达式：

将式(44)和式(45)代入式(43)可得：

则锚杆单一锚固区围岩径向应力表达式为：

式中：$f\left( {{r_0}} \right)$为待定系数；$f\left( r \right)$需用数值方法求解。

此时锚固区与原岩区径向接触力${p_{{r_{{\rm{sb}}}}}}$为：

联立式(34)、式(47)~式(48)并考虑式(37)即可得塑性区半径${r_{\rm{p}}}$，进而得到塑性区应力解答。代入式(22)并结合式(7)可得锚杆施作后塑性围岩变形表达式为：

式中，虚拟支护力采用式(24)计算。

4)对于${x^*} \leqslant x < {x_2}$段，锚杆端部位于塑性区内，将式(1)与式(32)联立并代入边界条件$r = {r_{\rm{p}}}$，${\sigma _r} = {\sigma _{\rm{p}}}$可得塑性原岩区应力表达式为：

将$r = {r_{\rm{s}}}$代入式(50)可得锚固区与原岩区界面处径向应力为：

因此，围岩变形采用式(49)计算，塑性区半径由式(37)、式(47)和式(51)求得，虚拟支护力采用式(24)。

5)对于$x \geqslant {x_2}$段围岩变形采用式(38)计算，塑性区半径由式(33)、式(37)、式(40)~式(41)求得，虚拟支护力采用式(24)。

2.3   工况C解析

当${x_{{\rm{cr}}}} < {x_2} < {x^*}$时锚索施作时围岩处于塑性状态且锚杆伸入围岩弹性区，因此围岩变形的纵向发展规律亦分为五段：

1)对于$x < {x_1}$段围岩变形采用式(3)计算，而虚拟支护力采用式(42)；

2)对于${x_1} \leqslant x < {x_{{\rm{cr}}}}$段围岩处于弹性状态，围岩变形采用式(11)计算，虚拟支护力采用式(42)；

3)对于${x_{{\rm{cr}}}} \leqslant x < {x_2}$段围岩处于塑性状态且锚杆伸入弹性区，围岩变形采用式(49)计算，塑性区半径由式(37)、式(47)~式(48)联立求得，虚拟支护力采用式(24)；

4)对于${x_2} \leqslant x < {x^*}$段围岩处于塑性状态且锚杆、锚索均伸入弹性区，围岩变形采用式(38)计算，塑性区半径由式(37)联立式(33)~式(36)求得，虚拟支护力采用式(24)；

5)对于$x \geqslant {x^*}$段围岩变形采用式(38)计算，塑性区半径由式(33)、式(37)和式(40)~式(41)求得，虚拟支护力采用式(24)。

2.4   工况D解析

当${x_{{\rm{cr}}}} < {x_1} < {x_2} < {x^*}$时围岩塑性阶段锚杆施作且伸入弹性区，锚索施作时围岩处于塑性且锚杆伸入弹性区，因此围岩变形纵向发展规律亦分为五段：

1)对于$x < {x_{{\rm{cr}}}}$段围岩处于弹性阶段，围岩变形由式(3)计算，而虚拟支护力采用式(42)；

2)对于${x_{{\rm{cr}}}} \leqslant x < {x_1}$段围岩处于塑性阶段，围岩变形由式(22)计算，塑性区半径表达式为：

式中，虚拟支护力由式(24)计算。

3)对于${x_1} \leqslant x < {x_2}$段围岩处于塑性阶段且锚杆伸入弹性区，围岩变形由式(49)计算，塑性区半径由由式(37)、式(47)~式(48)联立求得，虚拟支护力采用式(24)；

4)对于${x_2} \leqslant x < {x^{\rm{*}}}$段围岩处于塑性阶段且锚杆、锚索均伸入弹性区，围岩变形采用式(38)计算，塑性区半径由式(37)联立式(33)~式(36)求得，虚拟支护力采用式(24)；

5)对于$x \geqslant {x^{\rm{*}}}$段围岩处于塑性阶段且锚杆伸入塑性区，锚索伸入弹性区，围岩变形采用式(38)计算，塑性区由式(33)、式(37)和式(40)~式(41)求得，虚拟支护力采用式(24)。

2.5   工况E解析

当${x_{{\rm{cr}}}} < {x_1} < {x^*} < {x_2}$时围岩变形的纵向发展规律亦分为五个阶段，其中前两个阶段与工况D相同，而对于${x_1} \leqslant x < {x^*}$时围岩处于塑性且锚杆伸入弹性区，此时围岩变形由式(49)计算，塑性区半径由式(37)、式(47)~式(48)联立求得，虚拟支护力采用式(24)。

当${x^*} \leqslant x < {x_2}$时围岩处于塑性状态且锚杆伸入塑性区，围岩变形采用式(49)计算，塑性区半径由式(37)、式(47)和式(51)求得，虚拟支护力采用式(24)；

当$x \geqslant {x_2}$时锚杆伸入塑性区且锚索伸入弹性区，此时计算方法与工况D最后一阶段相同。

2.6   工况F解析

当${x_{{\rm{cr}}}} < {x^*} < {x_1} < {x_2}$时锚杆在围岩塑性阶段施作且伸入塑性区，围岩变形的纵向发展分为四个阶段，其中前两个阶段与工况D相同，而对于${x_1} \leqslant x < {x_2}$时围岩处于塑性状态且锚杆伸入塑性区，当${x_1} > {x_{{\rm{cr}}}}$时锚杆施作处围岩已进入塑性，围岩已释放位移为：

则锚杆施作时围岩径向应变为：

将式(54)和式(45)代入式(43)可得：

将式(55)代入式(1)并积分可得塑性区围岩径向应力表达式为：

式中：$f'\left( {{r_0}} \right)$为待定系数；$f'\left( r \right)$需用数值方法求解。

此时围岩变形由式(49)计算，塑性区半径由式(37)、式(51)和式(56)联立求得，虚拟支护力采用式(24)。

当$x \geqslant {x_2}$时锚杆伸入塑性区且锚索伸入弹性区，此时计算方法与工况D最后一阶段相同。

3   验证与分析

3.1   分析工况与数值模型的建立

为了验证理论模型的正确性，选取三种典型工况与FLAC3D数值模拟进行对比分析，其中包含图2中锚固体系施作时围岩力学状态及其与围岩塑性区所有可能的位置关系。针对半径为7.5 m的隧道，静水应力场为10 MPa，隧道开挖进尺取1 m。由于模型的中心对称性，为节省计算时间仅需对其1/4进行建模分析，如图3所示。

图  3  数值计算模型及边界条件

Figure  3.  Numerical model and boundary conditions

下载: 全尺寸图片 幻灯片

三种工况所采用的统一围岩参数为$E = 1\;{\rm{ GPa}}$，$\mu = 0.3$，$f = 1$，锚杆参数为${F_{{\rm{sb}}}} = 50\;{\rm{ kN}}$，${E_{{\rm{sb}}}} = 210\;{\rm{ GPa}}$，${A_{\rm{b}}} = 5\;{\rm{ c}}{{\rm{m}}^2}$，${S_{{\rm{cb}}}} = {S_{{\rm{lb}}}} = 1\;{\rm{ m}}$，锚索参数为${F_{{\rm{sc}}}} = 200\;{\rm{ kN}}$，${E_{{\rm{sc}}}} = 200\;{\rm{ GPa}}$，${A_{\rm{c}}} = 10\;{\rm{ c}}{{\rm{m}}^2}$，${S_{{\rm{cc}}}} = {S_{{\rm{lc}}}} = 2\;{\rm{ m}}$，其他参数如表1所示。

表  1  典型工况围岩和锚固体系参数

Table  1.  Parameters of surrounding rock and anchorage system of typical cases

工况	围岩参数				锚杆参数			锚索参数
	m	s	${\sigma _{\rm{c}}}$/MPa		${x_1}$/m	${L_{{\rm{sb}}} }$/m		${x_2}$/m	${L_{{\rm{sc}}} }$/m
1	4	0.004	26		2	2.0		8	11
2	3	0.002	16		3	3.0		12	12
3	3	0.001	9		4	2.5		14	13

下载: 导出CSV 

| 显示表格

3.2   计算结果分析

各工况下锚固体系与围岩相互作用的演化路径判断过程如表2所示。以工况2为例，首先判断锚杆施作时围岩弹塑性状态，由于${x_{{\rm{cr}}}} = 1.58\;{\rm{ m < }}{x_1}$，因此锚杆施作时围岩处于塑性状态，进而计算锚杆施作时围岩塑性区半径可得${r_{\rm{p}}}_{\left| {x = {x_1}} \right.} = 7.84\;{\rm{ m}}$，由于${r_{\rm{p}}}_{\left| {x = {x_1}} \right.} < {r_{{\rm{sb}}}}$，因此锚杆施作时伸入弹性区，然后锚索施作时围岩塑性区半径进行计算，可得${r_{\rm{p}}}_{\left| {x = {x_2}} \right.} = 10.21\;{\rm{ m}}$，由于${r_{\rm{p}}}_{\left| {x = {x_2}} \right.} < {r_{{\rm{sb}}}}$，因此锚索施作时锚杆仍作用与弹性区，因此可确定演化路径为路径D，接着对锚杆前端恰位于弹塑性界面上的临界距离进行计算，可得${x^*} = 14.56\;{\rm{ m}}$，则对于$x > {x^*}$即为最终阶段。需要指出，对于工况3，围岩在开挖面前方即已进入塑性，且锚杆施作时塑性区范围已大于锚杆长度，因此为路径F。

表  2  锚固体系与围岩相互作用演化路径的判定

Table  2.  Determination of evolution path of interaction between anchorage system and surrounding rock

计算工况	${x_{{\rm{cr}}} }$/m	${r_{\rm{p}}}_{\left| {x = {x_1} } \right.}$/m	${x^*}$/m	${r_{\rm{p}}}_{\left| {x = {x_2} } \right.}$	演化路径
1	8.27	−	28.38	−	A
2	1.58	7.84	14.56	10.21	D
3	−3.61	10.65	−	13.82	F

下载: 导出CSV 

| 显示表格

计算可得各工况下围岩纵向变形和塑性区半径计算结果如图4所示。计算表明，基于本文计算模型得到的锚固体系作用下围岩纵向变形与数值模拟结果基本一致，而数值模拟的塑性区半径受网格影响较大无法比较，但其粗略值和发展趋势与本文计算结果是一致的，说明本文推导是正确的、可靠的。此外，由于锚固体系与围岩参数的差异，相互作用路径有所不同，由此造成围岩全过程变形演化过程的差异。遗憾的是，在以往的理论推导中并未考虑锚固体系与围岩相对位置差异与锚固时机的综合影响，这显然与实际情况是不符的。

图  4  各工况理论解析与数值模拟结果对比

Figure  4.  Comparison of theoretical analysis and numerical simulation results of each working condition

下载: 全尺寸图片 幻灯片

进一步以工况1为例与现有研究中考虑锚固体系等效加固圈或等效支护力单一作用的方法进行对比，可见，仅考虑锚固体系某一方面作用时围岩变形和塑性区半径计算值较本文结果偏大，且当围岩变形量越大时误差也随之增大，这表明以往理论低估了锚固体系的作用，而在大变形围岩条件中则更为明显，这显然是不可接受的。因此，采用本文解进行锚固体系的设计将更为合理，尤其对于大变形围岩条件优越性则更为显著。

4   隧道锚固体系变形控制效果分析

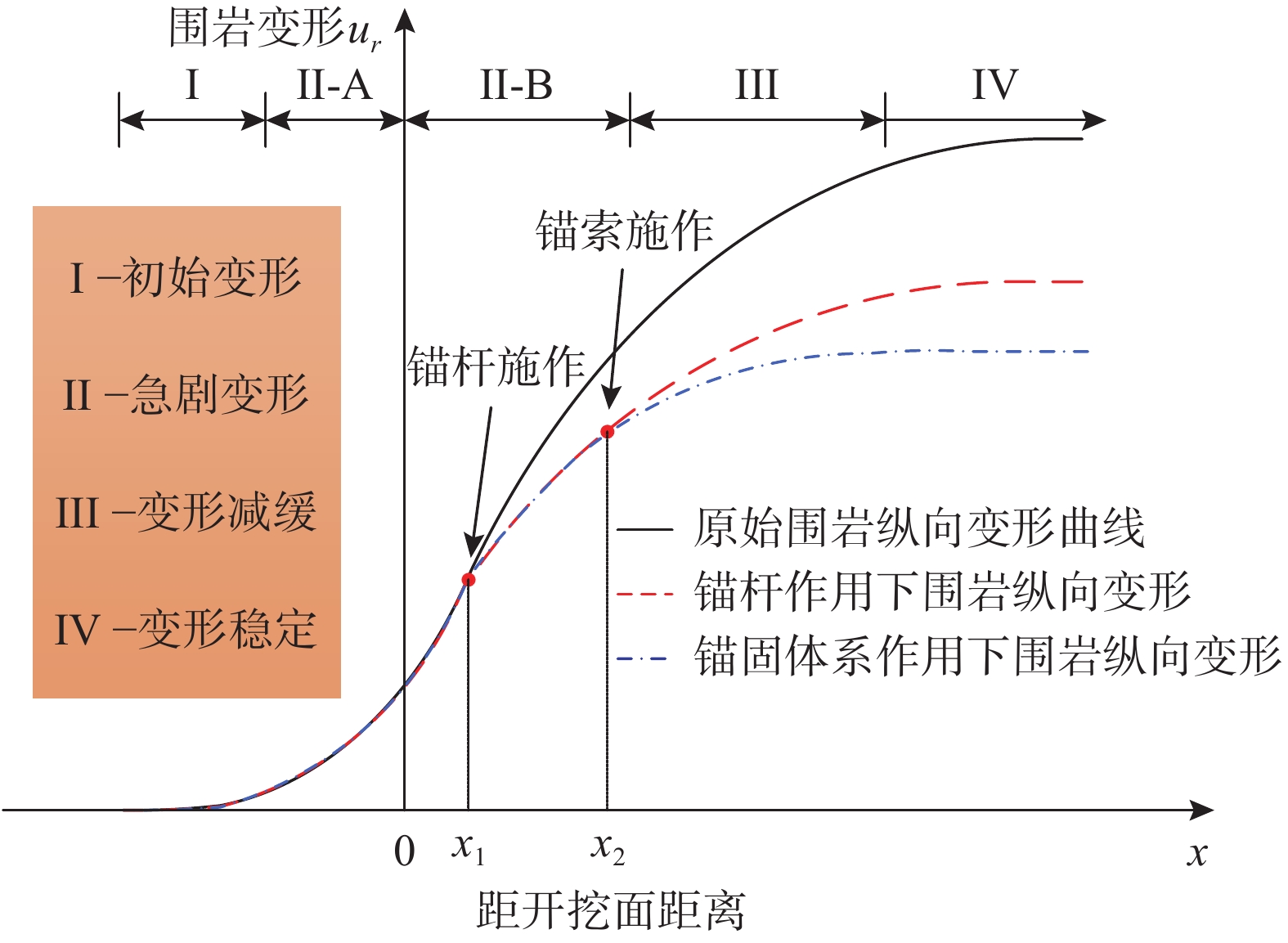
4.1   锚固体系对围岩全过程变形的控制原理

施工影响下隧道围岩纵向变形可依次划分为初始变形、急剧变形、变形减缓和变形稳定等4个阶段，如图5所示。其中急剧变形阶段所占比例最大，一般可占到总变形量的60%左右，根据控制重点的不同又可划分为开挖面前方和后方两个亚阶段，即图中II-A和II-B阶段。II-A阶段控制的核心为防止开挖面失稳，为隧道开挖创造条件，这一功能通常由超前支护实现；而II-B段则对应隧道围岩大变形控制，通过及时支护减小围岩急剧变形的时间，从而控制围岩变形量。锚固体系工作核心则是对II-B段围岩变形进行控制，减小急剧变形时间。

图  5  隧道锚固体系变形控制原理示意图

Figure  5.  Schematic diagram of deformation control principle of tunnel anchorage system

下载: 全尺寸图片 幻灯片

隧道锚固体系作业灵活性高且安装方便，可在开挖面形成后及时发挥作用。由前文分析可知，锚杆一方面通过对围岩加固从而提高锚固区围岩力学性能，即等效加固圈效应，另一方面施加径向约束从而控制围岩变形，即等效支护力效应。由图5可见，对于一般围岩条件，当仅有锚杆作用时围岩变形已得到控制。而当围岩变形控制较为严格时则需进一步采用刚度较大的锚索，通过锚固体系的协同作用实现对围岩变形的主动控制。

本质上来讲，隧道围岩变形的产生是围岩荷载与支护抗力博弈过程中不平衡力作用的结果，根据牛顿第二定律，此不平衡力越大则变形加速度越大，进而影响到围岩变形。而支护抗力与支护刚度相关，显然支护与围岩系统刚度越大则围岩变形速率越小，变形控制效果也越好。而锚固体系一方面通过等效支护力作用施加支护刚度，另一方面通过等效加固圈作用提高围岩刚度和强度，此双重作用使得支护—围岩系统刚度提高，从而有效控制围岩变形。此外，由于围岩变形的时空效应，锚固体系的施作时机和空间分布对围岩变形发展也有重要影响。

4.2   影响因素分析

锚固体系各参数对围岩变形的影响已有相应研究，而本节旨在说明锚杆与锚索对于围岩变形控制效果的相对影响程度。由于实际工程中锚杆与锚索密度的设计值有时相差较大，且对于锚固体系何时施作也尚无统一标准。考虑到锚固体系的等效支护力与加固程度均与密度有关，而施作时机则反映了围岩位移释放情况，因此选取这两个参数进行分析具有足够的代表性。

计算选取的围岩参数与节4.1中工况1相同，由于锚固体系间距和排距对围岩变形影响程度相当，因此设锚固体系支护密度为$C = {1 / {\left( {{S_{\rm{c}}}{S_{\rm{l}}}} \right)}}$，参考实际工程中锚固体系的设计方案并结合规范^[32]，确定各参数取值情况如表3所示。

表  3  锚固体系计算方案

Table  3.  Calculation scheme of anchorage system

参数	${x_1}$/m	${C_{\rm{b}}}$/(根/m2)	${x_2}$/m	${C_{\rm{c}}}$/(根/m2)
参考值	2	1	10	1
变化范围	1	0.25	8	0.25
	2	0.5	10	0.5
	3	1	12	1
	4	2	14	2
	5	4	16	4

下载: 导出CSV 

| 显示表格

采用前文公式计算可得锚固体系典型参数对隧道围岩全过程变形曲线的影响如图6所示。可见，随着锚杆支护时机的延迟和锚杆密度的减小，隧道围岩变形量显著增大，${x_1} = 5\;{\rm{ m}}$时围岩最大变形量比${x_1} = 1\;{\rm{ m}}$时增大约23%，而${C}_{{\rm{b}}}=0.25\;{\text{根}}{\rm{/m}}^{2}$时围岩最大变形量比${C}_{{\rm{b}}}=4\;{\text{根}}{\rm{/m}}^{2}$时增大约54%，这表明锚杆支护参数对围岩变形控制效果影响十分明显。随着锚索密度的减小，围岩最大变形量也有一定程度的增大，${C}_{{\rm{b}}}=0.25\;{\text{根}}{\rm{/m}}^{2}$时围岩最大变形量比${C}_{{\rm{b}}}=4\;{\text{根}}{\rm{/m}}^{2}$时增大11%。特别地，锚索密度为${C}_{{\rm{b}}}=4\;{\text{根}}{\rm{/m}}^{2}$与${C}_{{\rm{b}}}=2\;{\text{根}}{\rm{/m}}^{2}$时围岩变形相差不大，因此实际工程中锚索无需布置过密，而锚索支护时机的延迟对围岩变形量无明显影响。

图  6  隧道锚固体系典型参数对围岩全过程变形影响分析

Figure  6.  Influence of typical parameters of tunnel anchorage system on the whole process of surrounding rock deformation

下载: 全尺寸图片 幻灯片

因此，锚固体系对围岩变形的控制效果主要受锚杆参数的影响，而锚索对围岩变形影响不如锚杆显著，由此可确定锚索的安全储备作用，应在锚杆—围岩变形发展至一定程度后施作，其意义主要在于对于大变形围岩情况增大锚固系统的整体刚度，并保证运营期间锚固体系的安全储备系数。

5   结论

本文基于隧道开挖面空间效应，考虑锚固体系支护时机的相对滞后性及锚固区与塑性区边界的空间位态关系，建立了锚固体系与围岩相互作用的全过程演化机制模型，进一步分析了锚固体系的变形控制效果及其影响因素，对锚固体系与围岩相互作用全过程给出了全新的认识，据此可实现锚固体系的定量化设计。得到如下主要结论：

(1)由于锚杆、锚索支护时机及长度的差异性，二者施作时围岩可能处于不同的应力状态，而相互作用过程中锚固区与塑性区的空间位态也在不断变化，据此将锚固体系与隧道围岩作用全过程分为6种发展路径并进行解析，获得了不同路径下围岩变形与塑性区半径的演化规律。

(2)通过选取典型的计算工况与数值模拟结果进行对比，验证了本文综合考虑等效支护力和加固圈效应进行推导的正确性，并与考虑锚固体系单一作用的结果进行对比分析，指出现有理论低估了锚固体系作用，而对于大变形围岩条件是不可接受的。

(3)分析了锚固体系的变形控制原理，锚固体系作为主动支护形式，一方面通过提供径向约束改善围岩受力状态，另一方面提高锚固区围岩力学性能，本质上是增大支护—围岩系统刚度，从而实现对围岩急剧变形量的控制。

(4)由于锚固体系与围岩相对位置的变化，在不同的锚固时机和锚固长度影响下隧道围岩计算工况具有较大差异，而此差异在以往理论推导中并未考虑，由此造成围岩变形和塑性区计算结果与实际情况有所出入。

(5)计算分析表明，锚固体系的变形控制效果主要受锚杆影响，而由于锚杆施作时围岩已发生一定程度的变形，为保证支护效果应尽早施作。对于一般围岩条件，锚索延伸率低滞后于锚杆施作，此时围岩变形已得到较大释放，锚索参数对围岩变形影响较弱，由此可确定锚索的安全储备作用。