线性动力吸振器因其结构简单、便于安装而被广泛用于结构的振动控制中^[1-2]。为了提高线性吸振器的减振效果，学者们将多种形式的耗能、吸振组件引入其中，例如引入碰撞^[3-5]和内共振^[6]。碰撞调谐质量阻尼器(pounding tuned mass damper, PTMD)是在悬挂质量摆(suspended mass pendulum, SMP)基础上增设限位装置，通过质量块与限位器碰撞增加阻尼器的耗能能力。研究表明：PTMD的减震性能优于SMP，并且具有很好的鲁棒性^[7-9]。弹簧摆(spring pendulum, SP)是用弹簧替代了SMP的摆线，依靠弹簧内共振增加阻尼的吸振能力^[10]。在本文作者的工作中^[11]，将碰撞阻尼与弹簧摆相结合，提出了一种新型非线性阻尼器，即弹簧摆碰撞调谐质量阻尼器(spring pendulum pounding tuned mass damper, SPPTMD)。SPPTMD由弹簧摆及限位装置构成，通过弹簧内共振及质量块与限位器碰撞耗能。研究结果表明：SPPTMD具有良好的减震效果。

在振动控制系统的设计中，减振装置的参数及布置位置的选取对减振效果的影响很大^[12-13]，对这些变量进行优化是很有必要的。智能优化算法根据原理不同可分为三类：基于生物学原理的优化算法、基于物理学原理的优化算法和其他类型的优化算法^[14]。基于生物学原理的优化算法是对生物进化行为的模拟，包括遗传算法、人工鱼群算法、萤火虫算法和粒子群算法等。GRECO等^[15]利用遗传算法，以建设成本和减振率为优化目标，对阻尼器进行了优化。金波等^[16]基于改进遗传算法对粘滞阻尼器的位置及数量进行了优化。张晓峰等^[17]和周红杰等^[18]分别采用人工鱼群算法和多岛遗传算法，对用于漂浮式风力机振动控制的TMD参数进行了优化。龙关旭等^[19]通过萤火虫算法和模拟退火算法，对用于大跨斜拉桥振动控制的阻尼器参数进行了优化。王小金等^[20]采用粒子群算法对用于高层结构减振的TMD参数进行了优化。基于物理学原理的优化算法包括模拟退火算法和混沌优化算法等。赖文龙等^[21]提出了基于模拟退火算法的阻尼器位置优化。KAVEH等^[22]采用混沌优化算法优化了TMD的参数。其他算法包括和声搜索算法、差分进化算法等。NIGDELI和BEKDAŞ ^[23]采用和声搜索算法，以结构顶层加速度传递函数最小为优化目标函数，对TMD的质量、周期和阻尼系数进行了优化。LE-DUC等^[24]将差分进化算法与无梯度全局优化算法结合，对各种类型的磁流变阻尼器参数进行了优化。上述研究均表明，对减振装置进行优化设计能有效地提高其抑振性能。

尽管已有研究表明：SPPTMD具有较好的减震性能，但其设计参数(包括频率比、弹簧内共振系数、碰撞间隙等)尚需进一步优化设计才能达到更好的减震效果。

粒子群算法适合在动态、多目标优化环境中进行寻优计算。与众多优化算法相比，粒子群算法需要调整的参数较少，算法结构简单，并且具有更高效的并行计算能力，可以在较短时间搜寻到全局最优^[25-26]。另外，粒子群算法对种群数量变化不是十分敏感，寻优性能稳定^[27-28]。因此，本文采用鲁棒性强并且收敛快的粒子群算法，对SPPTMD的参数进行优化。以结构最大位移最小为目标函数，并且选取多条地震动验证了优化后SPPTMD的减震性能。

1   结构-SPPTMD系统模型

1.1   SP减振机理

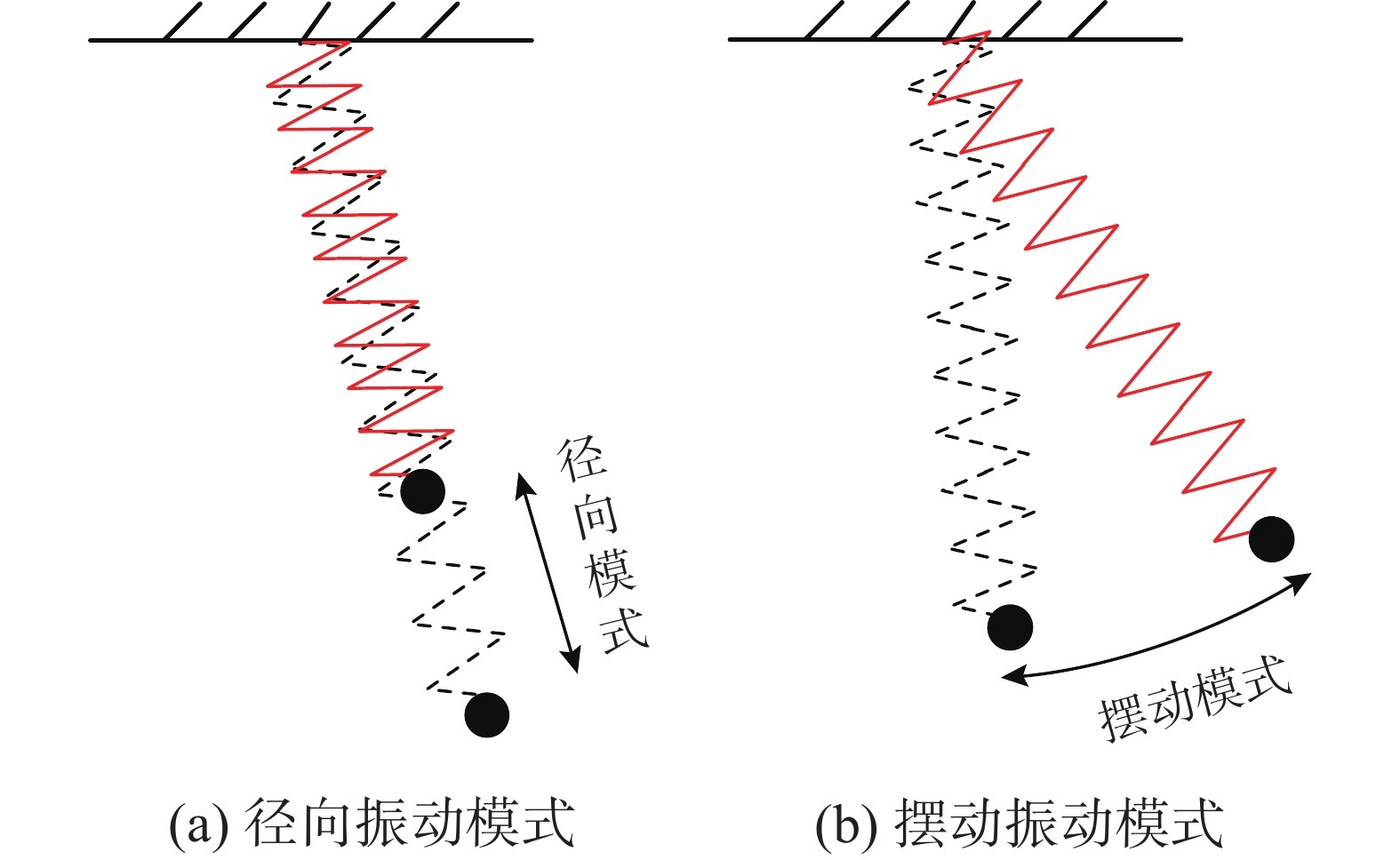
SP可认为是一种改进的SMP，即用弹簧代替摆线。SP具有两种圆频率：径向振动模式圆频率 ${\omega _{\rm{s}}}$和摆动振动模式圆频率 ${\omega _{\rm{p}}}$(图1^[11])。

图  1  SP的振动模式

Figure  1.  Vibration modes of the SP

下载: 全尺寸图片 幻灯片

研究发现^[29]，当满足特定条件时，两种振动模式将强烈耦合，振动能量会在两种振动模式之间不断传递，被称为内共振现象，根据内共振条件可得弹簧刚度为：

式中： ${k_{\rm{s}}}$为弹簧的刚度； $\lambda = \dfrac{{{\omega _{\rm{s}}}}}{{{\omega _{\rm{p}}}}}$为弹簧内共振系； ${m_{\rm{d}}}$为质量块的质量； $g = 9.8\;{\rm{m}}/{{\rm{s}}^2}$为重力加速度； ${l_{\rm{o}}}$为弹簧在重力作用下的长度：

式中： $f$为主结构频率； $\varOmega = \dfrac{{{\omega _{\rm{p}}}}}{f}$为阻尼器频率比。

内共振现象将放大SP的动力吸振能力，相比于悬挂质量摆，满足内共振时SP的减振效率更高。然而，已有SP仍存在耗能能力不足问题，故引入碰撞耗能模式，提出了弹簧摆碰撞调谐质量阻尼器(SPPTMD)。

1.2   SPPTMD减振机理

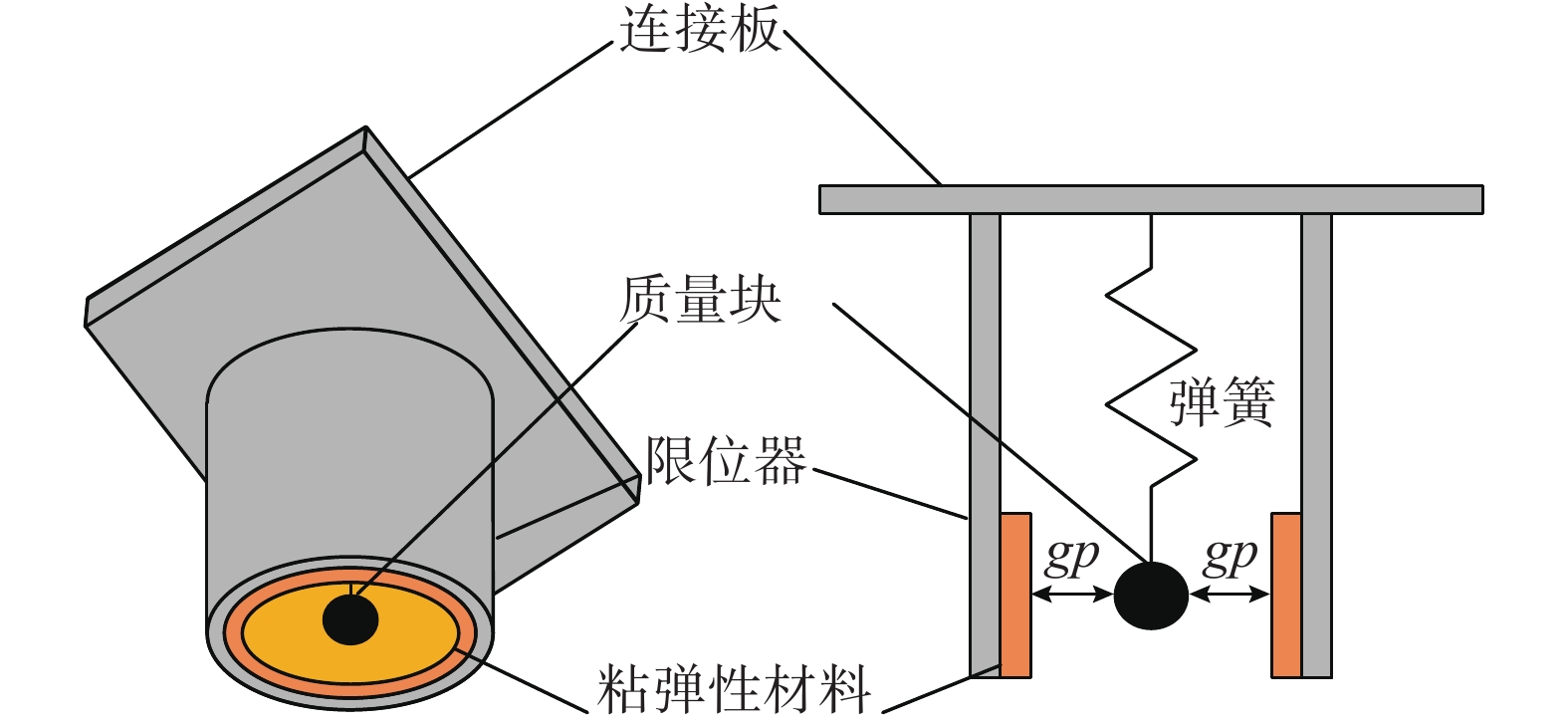
SPPTMD是在SP的基础上增设限位器(如图2所示^[11])，它是依靠SP及附加质量与限位器碰撞来耗能的非线性吸振器。在结构振幅较小时，附加质量与限位器没有发生碰撞，SPPTMD退化为传统SP；当结构振幅较大时，附加质量与限位器发生碰撞，此时SPPTMD通过撞击消耗阻尼器吸收的系统动能。

图  2  SPPTMD示意图

Figure  2.  Schematic of the SPPTMD

下载: 全尺寸图片 幻灯片

1.3   结构-SPPTMD系统模型的建立

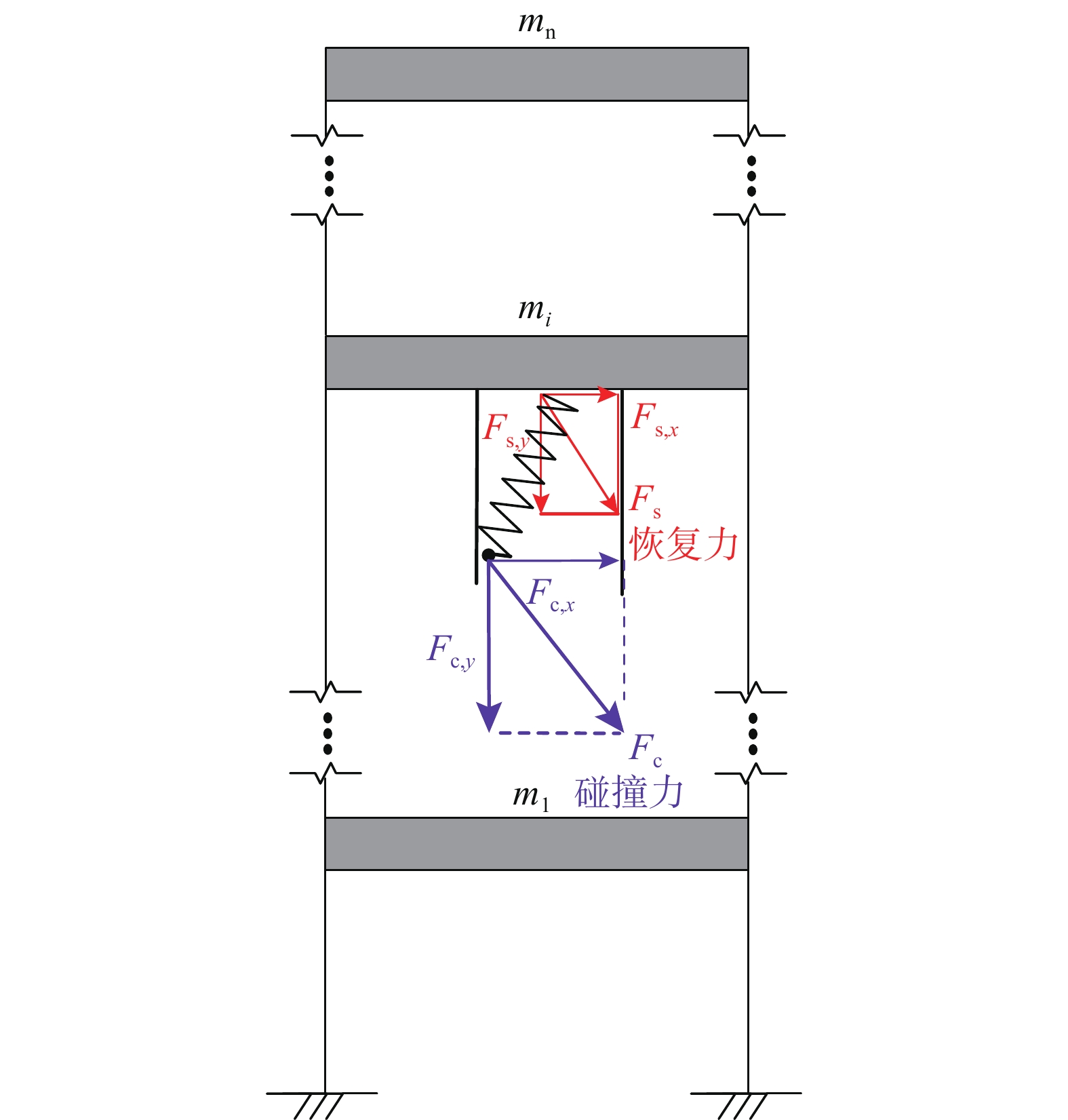
假设，SPPTMD附加在一个n自由度体系的第i个自由度上(如图3所示^[11])，则结构-SPPTMD体系的运动方程为：

图  3  第i个自由度上的控制力

Figure  3.  Controlling forces imposed on the i-th DOF

下载: 全尺寸图片 幻灯片

式中： ${{\boldsymbol{M}}_{\rm{s}}}$、 ${{\boldsymbol{C}}_{\rm{s}}}$和 ${{\boldsymbol{K}}_{\rm{s}}}$分别为无控结构的质量矩阵、阻尼矩阵和刚度矩阵； ${\boldsymbol{\ddot x}}(t)$、 ${\boldsymbol{\dot x}}(t)$ 和 ${\boldsymbol{x}}(t)$分别为无控结构的加速度、速度和位移； ${\boldsymbol{I}}$为1的列向量； ${\ddot x_g}$为地面加速度； ${\boldsymbol{L}}$为SPPTMD的位置向量； ${F_{{{\rm{s}},x}}}$和 ${F_{{\rm{c}},x}}$分别为附加质量在x方向的恢复力和碰撞力； ${F_{\rm{dir}}}$为碰撞力方向； ${x_{\rm{d}}}$和 ${y_{\rm{d}}}$分别为质量块在水平和垂直方向的位移； ${F_{{\rm{s}},y}}$和 ${F_{{\rm{c}},y}}$分别为附加质量在y方向的恢复力和碰撞力。SPPTMD的位置向量 ${\boldsymbol{L}}$可写成：

由于限位器是环形的，左右两侧都能发生碰撞。碰撞力方向 ${F_{\rm{dir}}}$为：

根据之前的研究，可以得恢复力和碰撞力的公式：

式中： ${x_i}$为无控结构第i个自由度的水平方向的位移； ${l_{\rm{ori}}}$为弹簧原长。

假设质量块与边界的间距是 ${g_{\text{p}}}$，根据Hertz接触单元和非线性阻尼的碰撞力模型可得SPPTMD的碰撞力为^[30]：

式中： $\beta$为碰撞刚度； $\delta$为粘弹性材料的相对变形； $c$为碰撞阻尼。 $\delta$和 $c$可由下面2个公式计算：

式中： $\xi$为碰撞阻尼比； ${m_i}$为无控结构第i个自由度的质量。 $\xi$可由下式计算:

式中， $e = \sqrt {\dfrac{{{h^ * }}}{h}}$为恢复系数，可以通过落球实验测得：使球体在 $h$高度处自由下落，测得其反弹高度 ${h^ * }$。

2   粒子群算法的优化过程

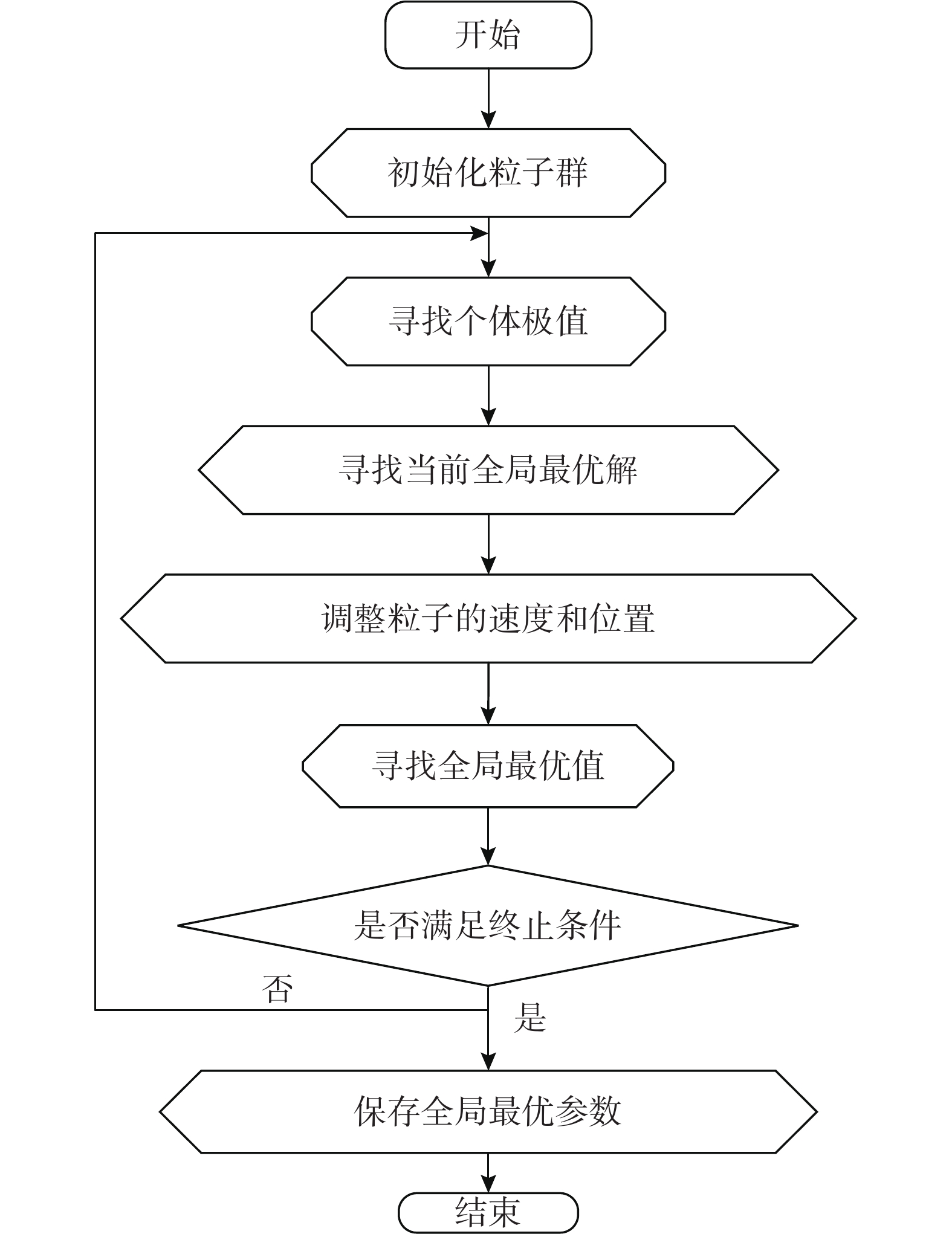
为解决SPPTMD参数优化问题，本文以结构最大位移最小为优化目标，以SPPTMD阻尼比、内共振系数和碰撞间隙为优化变量，采用粒子群算法进行优化设计。粒子群算法最早是由KENNEDY和EBERHART^[31]提出的，其基本思想是：每个粒子将其在空间中搜寻到的最优解记为个体极值，将粒子的个体极值在粒子群中共享，找到整个粒子群当前的最优解，并将其记为当前全局最优解。每个粒子根据当前的个体极值及全局最优解来调整粒子的速度和位置，直到找到全局最优解。

粒子群寻优过程如图4所示：

图  4  优化流程图

Figure  4.  Optimization flow chart

下载: 全尺寸图片 幻灯片

步骤1：初始化粒子群，例如设置粒子群规模、惯性因子、学习因子、优化变量初始值、粒子群更新速度、最大迭代次数；

步骤2：根据目标函数，计算每个粒子的适应度值，寻找个体极值；

步骤3：粒子间共享个体极值，找到当前粒子群的全局最优解；

步骤4：每个粒子根据当前速度、位置、和全局最优值调整下一步的速度和位置；

步骤5：不断的迭代寻找全局最优值；

步骤6：保存全局最优值及最优参数，寻优过程结束。

本文将有控和无控结构顶点最大位移的比值最小作为优化目标，目标函数为：

式中， ${D_0}$和 ${D_1}$分别为结构在无控和有控时的顶点最大位移。

3   数值算例分析

3.1   工程实例

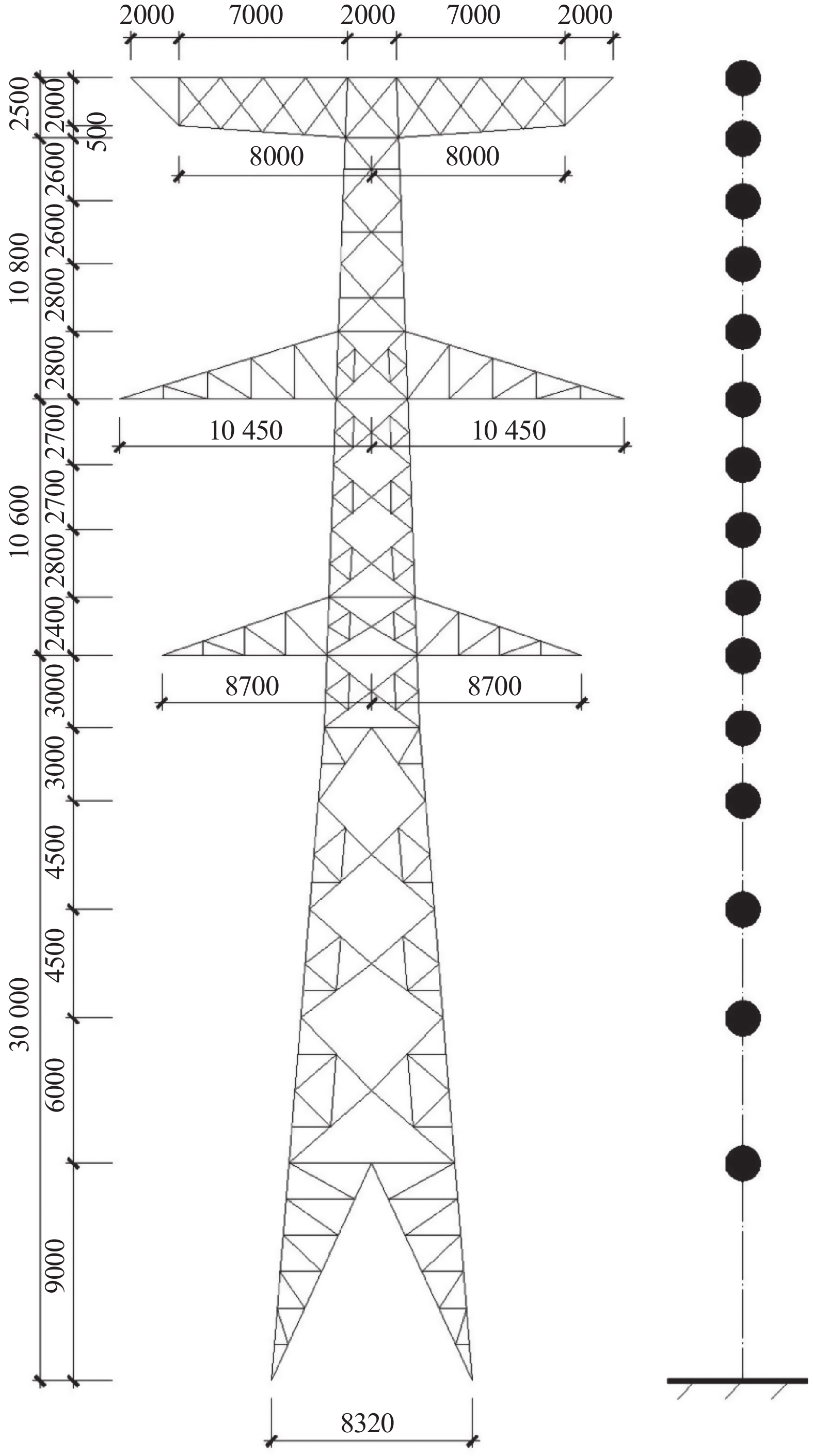
以某53.9 m高的输电塔为振动控制研究对象。如图5所示，输电塔被简化为15个自由度，一阶频率为 1.87 Hz。为了说明优化方法的有效性，本文将优化前、后SPPTMD的减震效果进行了比较。其中，定义未优化的SPPTMD频率比为1，质量比为3%，内共振系数为2，碰撞刚度为17 000 N/m^3/2，碰撞间隙为0.05 m，SPPTMD通过螺栓连接到输电塔的顶部。对SPPTMD的频率比、内共振系数和碰撞间隙进行优化，使结构顶点位移最小。

图  5  输电塔示意图

Figure  5.  Schematic of the transmission tower

下载: 全尺寸图片 幻灯片

定义减震率为：

3.2   地震动选取

为了优化SPPTMD在I类、II类、III类、IV类场地中的减震性能，每类场地选取了3条地震动进行研究，峰值加速度调整为400 cm/s²，地震记录相关信息如表1所示，反应谱曲线如图6所示。

表  1  地震记录

Table  1.  Seismic records

场地类别	编号	名称	日期	站台
I	EQ1	Chuetsu-oki	2007	Kawaguchi
	EQ2	Darfield New Zealand	2010	Pages Road Pumping
	EQ3	Iwate	2008	Yuzawa
II	EQ4	San Fernando	1971	Hemet Fire
	EQ5	San Fernando	1971	2516 Via Tejon PV
	EQ6	Landers	1992	Desert Hot Springs
III	EQ7	Chuetsu-oki	2007	Tokamachi Matsunoyama
	EQ8	El Mayor-Cucapah	1910	EJIDO SALTILLO
	EQ9	El Mayor-Cucapah	1910	TAMAULIPAS
IV	EQ10	Hollister-01	1961	Hollister City Hall
	EQ11	Chi-Chi	1999	CHY067
	EQ12	Darfield New Zealand	2010	Shirley Library

下载: 导出CSV 

| 显示表格

图  6  加速度反应谱

Figure  6.  Acceleration response spectrum

下载: 全尺寸图片 幻灯片

3.3   结果分析

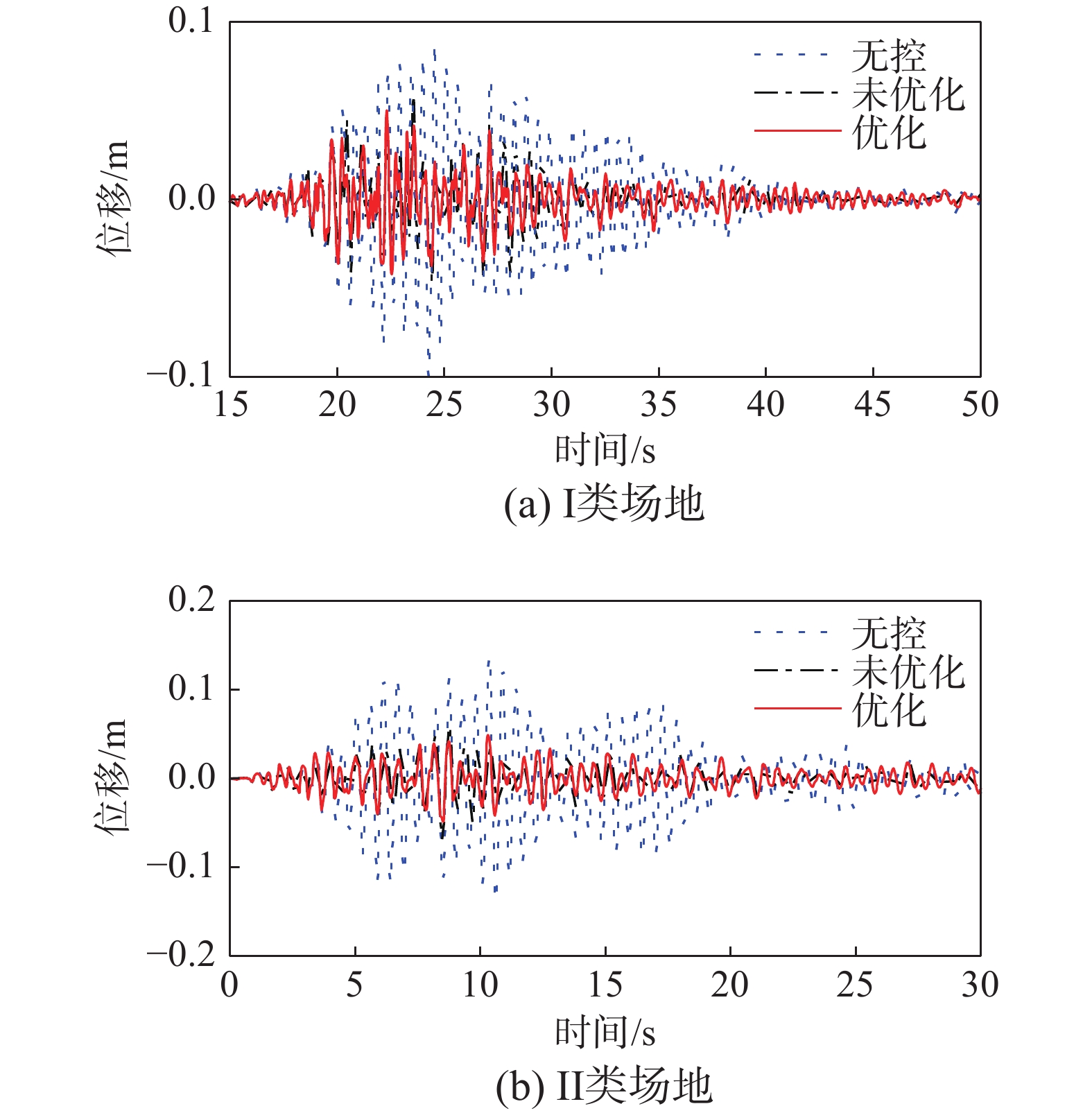
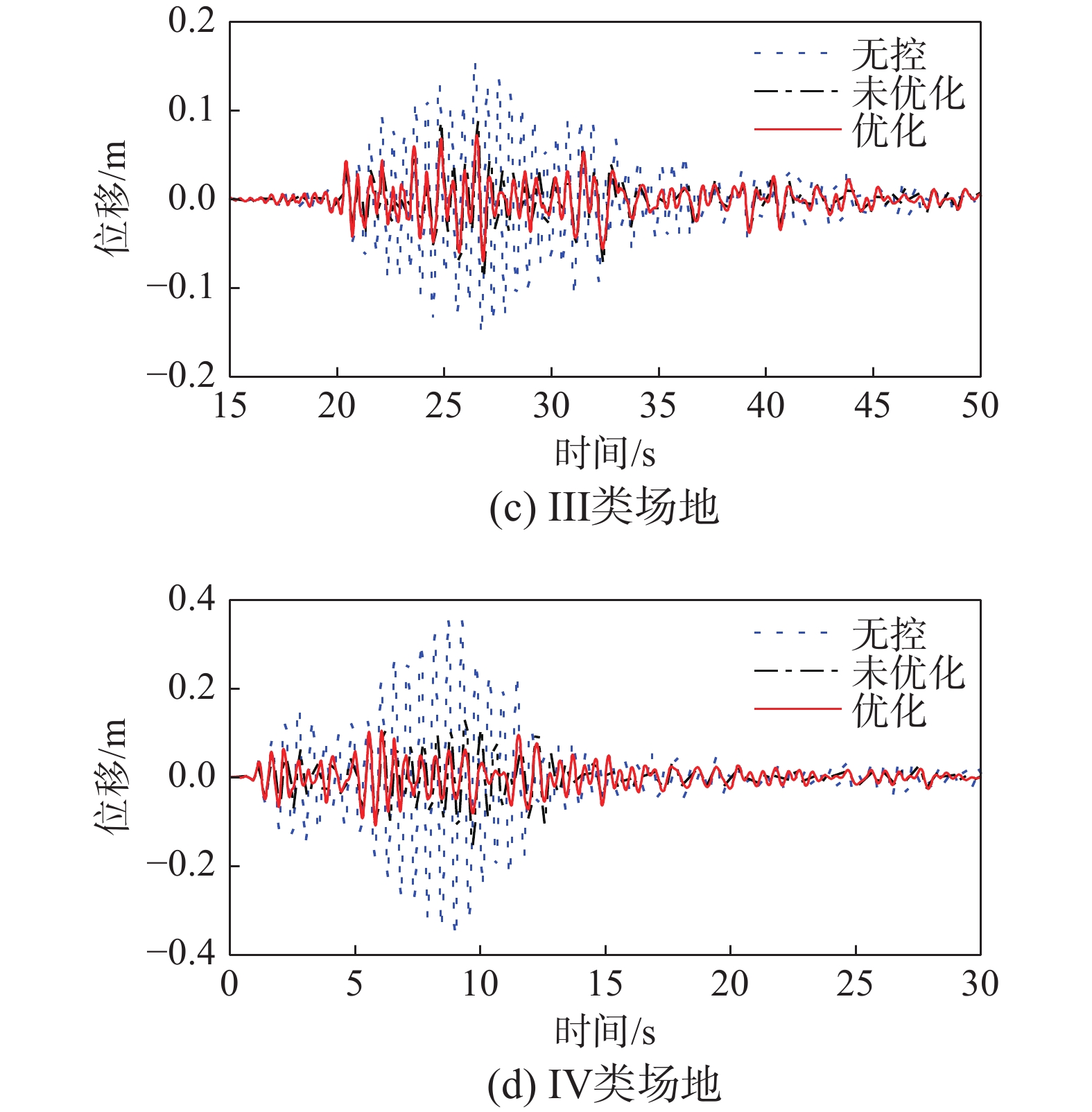
优化结果如表2所示，表3列出了结构峰值位移减震情况，由于所选取的地震动较多，文中只给出了4条地震动作用下结构的位移响应(如图7、图8所示)。

表  2  最优参数

Table  2.  Optimal parameters

场地类别	频率比	内共振系数	碰撞间隙/m
I	0.76	2.67	0.10
II	0.78	2.26	0.06
III	0.84	1.69	0.04
IV	0.84	1.45	0.10

下载: 导出CSV 

| 显示表格

表  3  减震率

Table  3.  Vibration reduction ratios

场地类别	工况	未优化/(%)	优化/(%)
I	EQ1	44.00	55.22
	EQ2	36.42	41.58
	EQ3	41.15	49.50
	Average	40.52	48.77
II	EQ4	48.65	64.13
	EQ5	47.37	47.63
	EQ6	29.86	44.28
	Average	41.96	52.02
III	EQ7	42.12	53.40
	EQ8	46.20	54.83
	EQ9	41.18	52.00
	Average	43.17	53.41
IV	EQ10	57.88	69.36
	EQ11	44.10	61.24
	EQ12	46.02	55.92
	Average	49.34	62.17

下载: 导出CSV 

| 显示表格

下载: 全尺寸图片 幻灯片

  7  地震动作用下结构位移时程曲线

  7.  Displacement time history of the structure under the seismic

下载: 全尺寸图片 幻灯片

图  8  地震动作用下结构位移包络图

Figure  8.  Envelope of displacement of the structure under the seismic

下载: 全尺寸图片 幻灯片

从计算结果可以看出，任何工况下SPPTMD减震率均在36%以上。未优化的SPPTMD在I类、II类、III类、IV类场地中的峰值减震率的均值都在40%以上，分别为40.52%、41.96%、43.17%和49.34%，其中IV类场地中的减震率比I类场地增加了8.82个百分点。优化后的SPPTMD峰值减震率的均值都在48%以上，分别为48.77%、52.02%、53.41%和62.17%，其中IV类场地中的减震率比I类场地增加了13.4个百分点。

与优化前相比，I类~IV类场地中SPPTMD减震率均值分别提高了8.25、10.06、10.24和12.84个百分点。可见，SPPTMD的振动控制性能随着场地类别的提升而提升；优化后，SPPTMD在IV类场地中的抑振性能提高的幅度最大。综上所述，编制的优化程序能够有效优化SPPTMD的参数，提升阻尼器的减震性能。

4   结论

为了提高SPPTMD的振动控制性能，采用粒子群算法对SPPTMD参数进行了优化，并研究了不同场地地震动作用下SPPTMD的减震效果，得出了以下主要结论：

(1)对不同场地类别的结构进行振动控制时，SPPTMD的最优参数也不同，且存在如下规律：场地类别越坚硬，频率比越低，内共振系数越大。

(2) 场地土越软弱SPPTMD的振动控制性能越好，I类场地减震率最低，IV类场地减震率最高。

(3)优化后，SPPTMD减震率有大幅提高，减震率均值最高可达60%，说明编制的优化程序能够有效优化SPPTMD的参数。