FAST馈源舱结构气动力特性及耦联系统风振响应研究

李宏男; 张鸿志; 李庆伟; 付兴

doi:10.6052/j.issn.1000-4750.2023.02.0086

FAST馈源舱结构气动力特性及耦联系统风振响应研究

李宏男^1,,
张鸿志^1,,
李庆伟^2,,
付兴^1, ,

1.
大连理工大学建设工程学部土木工程学院，辽宁，大连 116024
2.
中国科学院国家天文台，北京 100010

基金项目: 国家自然科学基金项目(52027811，11973006)；大连市高层次人才创新支持计划项目(2019RD01)

详细信息

作者简介:
李宏男(1957−)，男，辽宁人，长江学者特聘教授，博士，主要从事工程结构抗震、抗风、健康监测与诊断研究(E-mail: hnli@dlut.edu.cn)

张鸿志(1999−)，男，黑龙江人，硕士生，主要从事工程结构防灾研究(E-mail: a1602081994@163.com)

李庆伟(1980−)，男，北京人，高工，硕士，主要从事大射电望远镜关键技术研究(E-mail: qwli@nao.cas.cn)

通讯作者:
付　兴(1988−)，男，辽宁人，副教授，博士，主要从事工程结构抗多灾及韧性评估研究(E-mail: fuxing@dlut.edu.cn)

中图分类号: TU312+.1；TU311.3
计量
- 文章访问数: 52
- HTML全文浏览量: 63
- PDF下载量: 20
出版历程
- 收稿日期: 2023-02-05
- 修回日期: 2023-04-09
- 录用日期: 2023-04-22
- 网络出版日期: 2023-04-25

RESEARCH ON THE AERODYNAMIC CHARACTERISTICS OF FAST FEED CABIN STRUCTURE AND THE WIND-INDUCED RESPONSES OF THE COUPLED SYSTEM

1.
School of Civil Engineering, Faculty of Infrastructure Engineering, Dalian University of Technology, Dalian 116024, China
2.
National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100010, China

摘要

摘要:
500 m口径球面射电望远镜的馈源舱工作在140 m高空，对风荷载敏感，过大风振响应可能影响馈源舱的正常工作。该文利用CFD数值模拟方法研究了馈源舱结构的气动力特性，确定了表面凸起部分对馈源舱结构气动力特性有极大影响，并发现240°风向是气动力系数最大的风向，180°为潜在涡激振动的风向，进而针对180°风向进行参数分析，计算了不同风速下的旋涡脱落频率和斯托罗函数。随后建立了完整的馈源舱-索塔耦联体系精细化有限元模型，模态分析结果表明：该结构体系的基频很小，且模态密集；在常遇风速内可依次激发结构的多阶模态。针对气动力系数最大的240°风向进行风振响应分析，计算了馈源舱-索塔耦联体系在工作风速和设计风速下的动力响应，结果表明：馈源舱在工作风速下的位移不会影响其工作精度，且在设计风速下整体结构处于安全水平；在开启和关闭二次精调平台时，最大工作风速分别可以达到9.3 m/s、4.3 m/s。
- 馈源舱结构 /
- 气动力特性 /
- CFD /
- 涡激振动 /
- 耦联体系 /
- 风振响应 /
- 有限元模型
Abstract:
The feed cabin of the five-hundred-meter aperture spherical radio telescope operates at an altitude of 140 meters, which is sensitive to wind load. Excessive wind-induced response may affect the normal operation of the feed cabin. The aerodynamic characteristics of the feed cabin structure are studied by CFD numerical simulation. The research results confirm that the surface bulge has a great influence on the aerodynamic characteristics of the feed cabin structure. According to the research results, the wind direction with the largest aerodynamic coefficient is 240 degree and the wind direction of potential vortex-induced vibration is 180 degree. Then the parametric analysis is presented for the 180 degree wind direction. The vortex shedding frequency and Strouhal number are calculated under different wind speeds. Besides, a complete refined simulation model of the feed cabin-cable-tower coupled system is established. The results of modal analysis show that the fundamental frequency of the structure is very low and the modes are dense. Multiple modes of the structure can be successively excited in normal wind speed. The wind response analysis is carried out for 240 degree wind direction with the largest aerodynamic coefficient. The dynamic responses of the feed cabin-cable-tower coupled system are calculated under the working wind speed and the design wind speed. The results show that the displacement of the feed cabin under the working wind speed will not affect its working accuracy, and the whole structure is in a safe level under the design wind speed. When the secondary fine-tuning platform is turned on and off, the maximum working wind speed can reach 9.3 m/s and 4.3 m/s, respectively.
- feed cabin structure /
- aerodynamic characteristics /
- CFD /
- vortex-induced vibration /
- coupled system /
- wind-induced response /
- finite element model

HTML全文

500 m口径球面射电望远镜(Five-hundred-meter Aperture Spherical radio Telescope，FAST)是目前世界上口径最大的射电望远镜。FAST在直径600 m的圆周上均匀布置六个支撑塔，通过六根拉索将馈源舱悬吊于空中，在百米尺度大空间内缓慢运动^[1-3]。FAST属于大跨空间结构，风荷载是结构设计的控制性荷载之一^[4-7]。

目前，针对FAST结构风振分析的研究成果还较少。吴明长等^[8]针对FAST反射面及其周边地形进行计算流体动力学(Computational fluid dynamics，CFD)数值模拟，确定了入口风剖面的基准高度，获得了35.4%透孔率的FAST反射面板的速度压降关系，计算了不同风向下反射面风压系数分布特征。段艳宾等^[9]利用MATLAB和Adams软件对FAST馈源舱-拉索系统进行了联合仿真，得到了馈源舱系统的动态特性，验证了外界风扰时馈源舱系统控制的可行性。魏书魁^[10]利用ANSYS软件对FAST馈源舱-拉索系统进行风荷载随机振动分析，并搭建了缩尺实验模型，验证了有限元模型分析数据的准确性和可靠性。

已有文献中，针对馈源舱-索塔体系的风振分析均忽略了支撑塔对系统的影响，且未针对馈源舱的气动力特性展开研究。因此本文首先对馈源舱进行CFD仿真模拟，研究馈源舱结构的气动力特性；再基于ANSYS软件，建立完整的馈源舱-索塔耦联体系模型，开展模态分析，获得结构振动特性；最后计算了该耦联体系在不同工况下的动力响应。

1 馈源舱结构CFD模型

1.1 几何模型和风向角定义

我国现行规范^[11]仅给出了几种简单结构的风荷载体型系数，针对馈源舱这种气动外形复杂的结构，规范中并无规定。目前，越来越多的复杂结构风荷载模拟采用数值分析方法^[12-16]，因此本文采用流体数值仿真方法研究馈源舱结构的气动力特性。馈源舱-索塔体系结构庞大，由于计算机资源的限制，本文仅建立馈源舱结构的CFD模型进行流体力学仿真分析。

馈源舱结构外径尺寸约为13 m，高度为4.19 m。实际的馈源舱结构表面为蒙皮表面，蒙皮上表面具有一些附属设施使模型表面具有一些凸起，如图1所示。

图 1 馈源舱结构实拍图

Figure 1. Picture of the feed cabin structure

下载: 全尺寸图片幻灯片

现有研究对馈源舱结构的建模均未考虑表面凸起^[17-18]，但表面凸起可能会影响结构表面的气体流动特性，为研究模型表面凸起对馈源舱结构气动力特性的影响，分别建立了无凸起和有凸起的馈源舱CFD仿真模型，如图2所示。图2(b)有两处大凸起，其尺寸完全相同，大凸起分为两层，贴近蒙皮一层的长宽均为0.55 m，高为0.2 m，远离蒙皮一层的长宽均为0.9 m，高为0.18 m；馈源舱边缘有一圈半厚为0.1 m的条型凸起，还有若干个长宽不超过0.9 m、高不超过0.2 m的块型凸起。

图 2 馈源舱CFD仿真模型

Figure 2. CFD simulation model of the feed cabin

下载: 全尺寸图片幻灯片

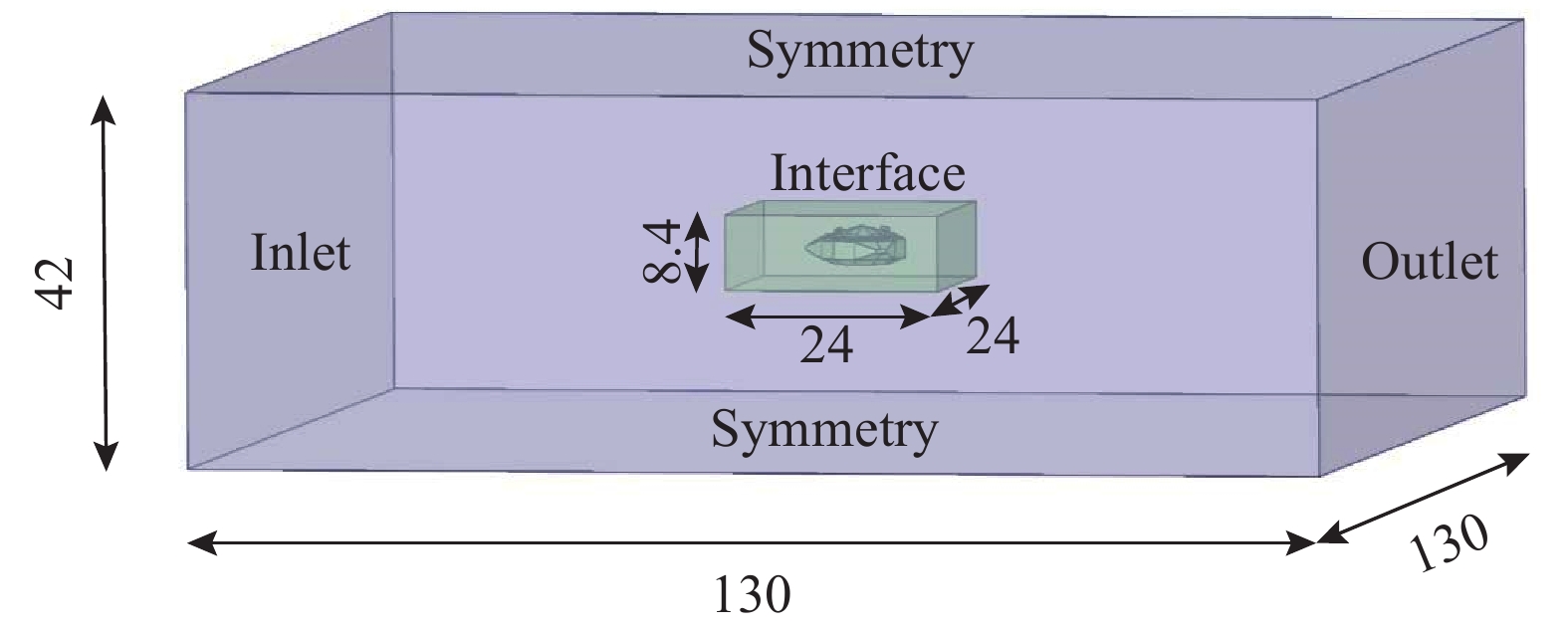
进而建立馈源舱结构计算域，为减小网格划分难度并减小计算量，将计算域分为内部和外部两个区域，如图3所示。外部计算域XYZ方向尺度为130 m×42 m×130 m，入口边界条件为velocity-inlet，出口边界条件为pressure-outlet，馈源舱表面边界条件为wall，其他边界条件均为symmetry；内部计算域XYZ方向尺度为24 m×8.4 m×24 m，边界条件均为interface。

图 3 计算域示意图　/m

Figure 3. Schematic of the computational domain

下载: 全尺寸图片幻灯片

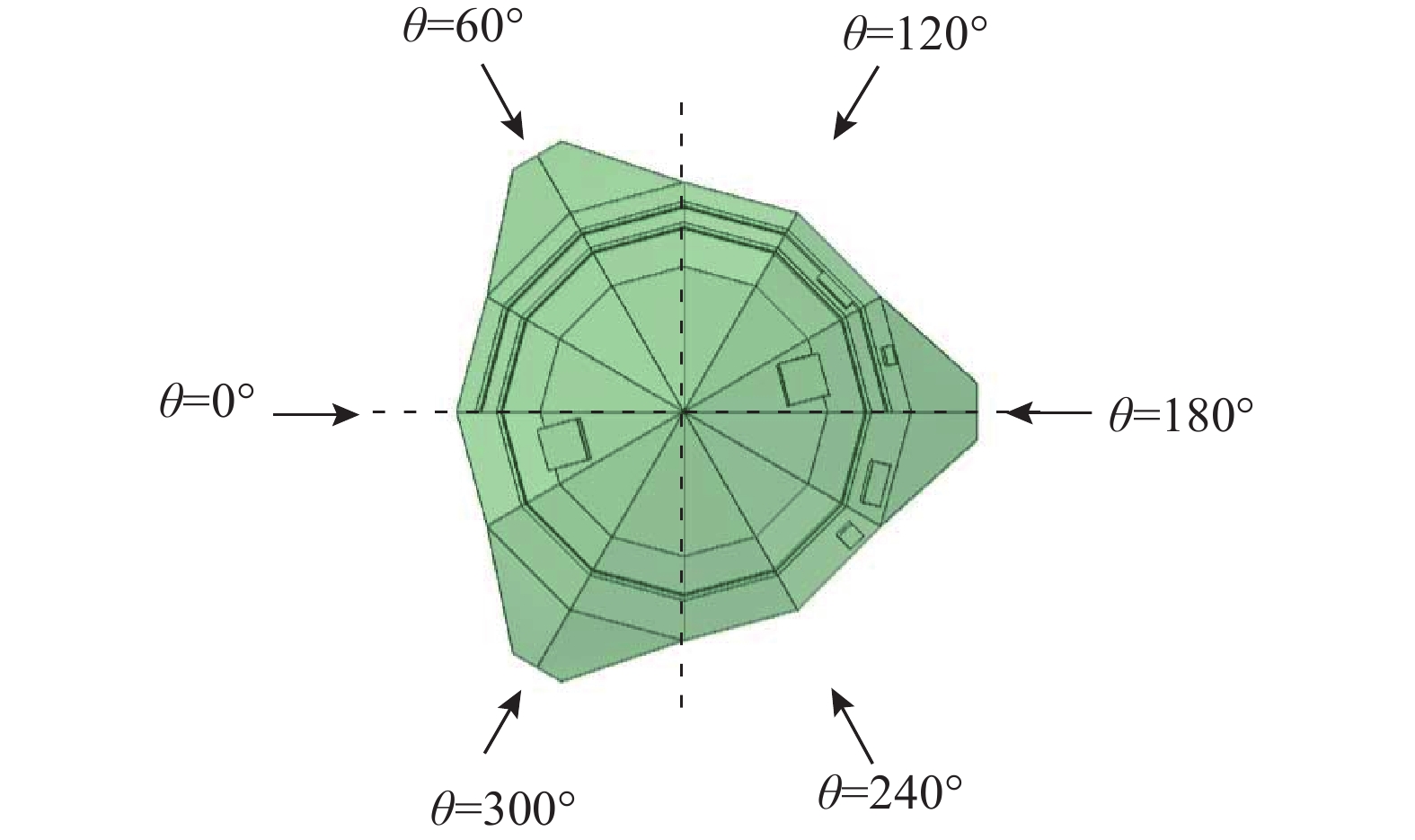
馈源舱结构风向角定义如图4所示，风向角沿顺时针方向转动增加。保持馈源舱模型位置不变，同时旋转计算域和坐标系至不同角度，保证X轴正方向和风速方向一致，以此方便获得不同风向的几何模型，在此基础上形成网格模型和CFD计算模型。

图 4 风向角定义

Figure 4. Definition of wind direction

下载: 全尺寸图片幻灯片

1.2 计算方法和参数处理

采用Fluent软件进行CFD仿真模拟，计算中采用基于压力的求解器，设置瞬态计算方法，时间步长均取0.1 s，湍流模型采用SST k-ω模型^[19]，采用SIMPLEC算法求解压力-速度耦合方程，压强项和动量项均为二阶格式，时间离散方程为二阶隐式格式，计算迭代的一般收敛准则为残差小于1×10⁻⁵。

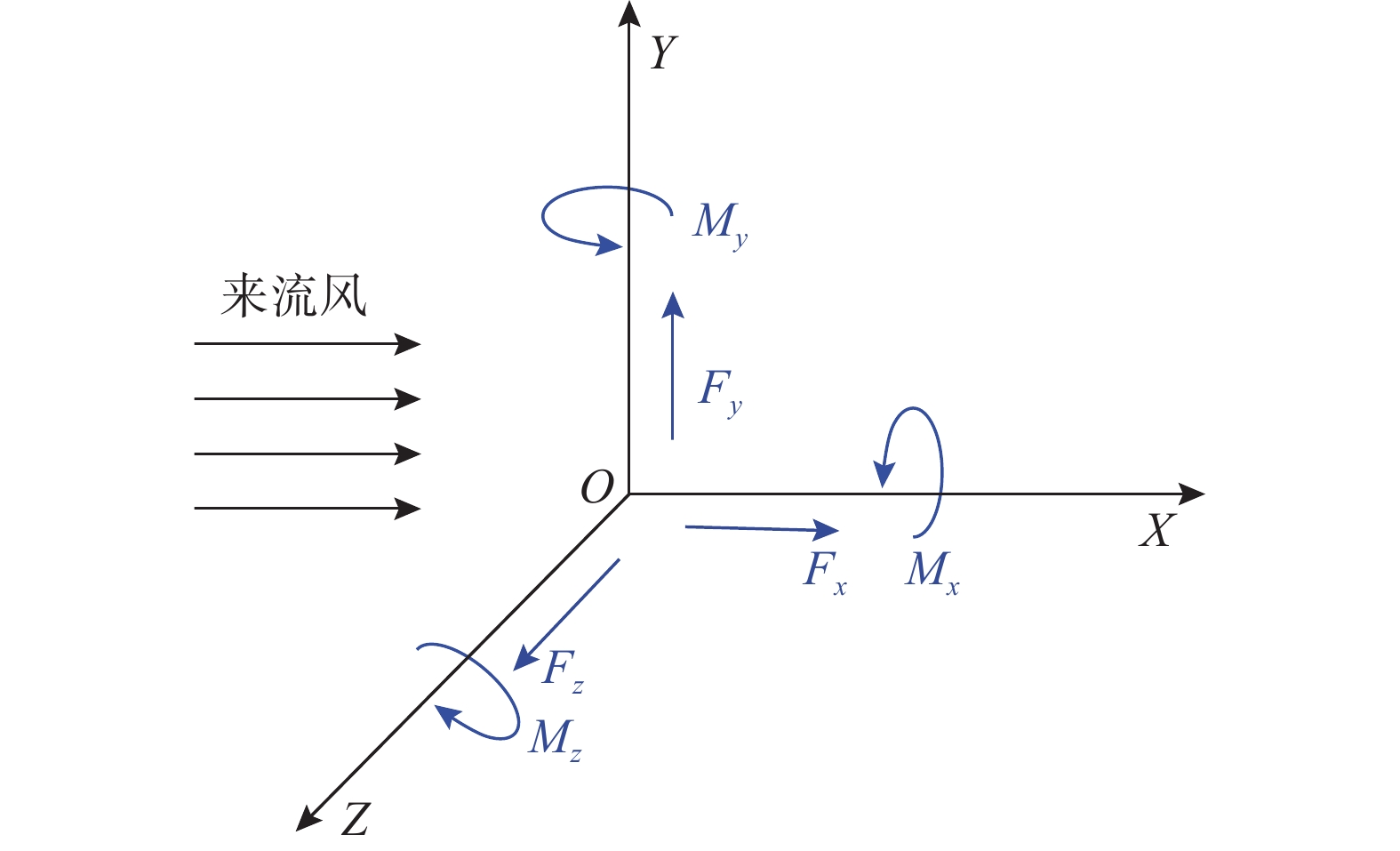
馈源舱模型在流场中承受六个方向的力，六分力的定义如图5所示。其中风速方向始终沿着X轴的正方向，Y轴正向竖直向上，所以分力F_x代表阻力，分力F_y代表升力，分力F_z代表侧向力，M_x、M_y和M_z分别代表绕三个坐标轴的力矩。

图 5 六分力示意图

Figure 5. Schematic of six-component force

下载: 全尺寸图片幻灯片

式(1)和式(2)是馈源舱结构六分力系数的具体计算公式，其中C_Fx对应阻力系数C_d，C_Fy对应升力系数C_l：

${C_{{F_i}}} = \frac{{{F_i}}}{{\dfrac{1}{2}\rho {U^2}A}}\;\;\;,\;\;i = x,\;y,\;{\textit{z}}$

(1)

${C_{{M_i}}} = \frac{{{M_i}}}{{\dfrac{1}{2}\rho {U^2}AL}}\;\;\;,\;\;i = x,\;y,\;{\textit{z}}$

(2)

式中：ρ为空气密度，本文取1.225 kg/m³；U为来流风速；A为结构在YOZ平面的投影面积，在图4中的六种风向下，结构投影面积相等，均为35.18 m²；L为投影面积A在Z轴的投影长度，为11.466 m。

1.3 网格模型

采用FLUENT MESHING^[20]中的Poly-Hexcore方法划分馈源舱流场域，生成多面体-六面体核心的混合网格，在馈源舱模型附近进行局部网格加密，保证计算的精确度。

对有凸起馈源舱模型建立四套网格进行网格无关性验证。方案M1对应的网格数量约337万，方案M2和M3分别在M1基础上进行内部和外部网格加密，对应网格数量约为608万和583万，方案M4为网格放大方案，网格数量约为114万。

以180°风向、2.7 m/s风速工况为例，各网格方案进行流场瞬态计算，时间步长取0.1 s。计算稳定且收敛后，得到的气动力系数时均值如表1所示。从表1中可知，阻力系数C_d和升力系数C_l均值较大，是馈源舱结构气动力特性的关键参数。内部加密方案M2的C_d系数和C_l系数均值相较于M1的误差分别为2.1%和6.7%，外部加密方案M3的C_d系数和C_l系数均值相较于M1的误差分别为0.2%和2.5%，方案M4的C_d系数和C_l系数均值相较于M1的误差分别为1.4%和133.6%。

各网格方案的阻力系数脉动均方根C_drms和升力系数脉动均方根C_lrms如表2所示。从表2中可知，M1、M2和M3的阻力系数和升力系数的脉动均方根都非常接近，而相较于前三种方案，M4的阻力系数和升力系数的脉动均方根都过小。经过比较，选用网格方案M1作为本文的计算网格，既保证了计算结果准确性又节约计算资源。

表 1 各网格方案气动力系数均值

Table 1. Average aerodynamic coefficients of each grid scheme

网格方案	网格数量	阻力系数C_d	升力系数C_l	侧向力系数C_Fz	倾覆力矩系数C_Mx	偏航力矩系数C_My	点头力矩系数C_Mz
M1	337万	0.2268	−0.0550	−0.0119	0.0068	−0.0002	0.0013
M2	608万	0.2316	−0.0587	−0.0189	0.0027	−0.0019	0.0005
M3	583万	0.2274	−0.0536	−0.0087	0.0069	−0.0002	0.0013
M4	114万	0.2299	−0.1285	0.0116	0.0022	0.0010	−0.0048

下载: 导出CSV

| 显示表格

表 2 各网格方案脉动均方根

Table 2. Pulsating root mean square of each grid scheme

网格方案	阻力系数脉动均方根C_drms	升力系数脉动均方根C_lrms
M1	0.0006	0.0036
M2	0.0007	0.0039
M3	0.0005	0.0034
M4	0.0001	0.0006

下载: 导出CSV

| 显示表格

上述M1网格方案的混合网格、局部加密网格及近壁面图如图6所示，网格数量约为337万，边界层第一层高度为0.03 m，总层数为10层。本文算例网格的Y+值均控制在20以内，满足壁面层计算要求。无凸起馈源舱模型网格划分方式与上述方法相同，网格数量约为303万。

图 6 馈源舱模型混合网格

Figure 6. Mixed grids of the feed cabin model

下载: 全尺寸图片幻灯片

另取0.02 s和0.05 s时间步长，进行步长无关性验证。以180°风向、2.7 m/s风速工况为例，进行200 s的流场瞬态计算，各步长算例计算稳定且收敛后，选取160 s~200 s的数据进行分析，得到的气动力系数时均值和脉动均方根如表3所示。从表中可以看出，随着时间步长的减小，阻力系数和升力系数的均值和均方根值变化非常小，说明0.1s时间步长结果收敛。

表 3 各时间步长算例气动力系数

Table 3. Aerodynamic coefficients of various time steps

时间步长/s	阻力系数 C_d	升力系数 C_l	阻力系数脉动均方根C_drms	升力系数脉动均方根C_lrms
0.10	0.2268	−0.0550	0.0006	0.0036
0.05	0.2267	−0.0543	0.0006	0.0036
0.02	0.2264	−0.0540	0.0007	0.0035

下载: 导出CSV

| 显示表格

2 馈源舱结构气动力特性

2.1 凸起对馈源舱结构气动力特性影响

以180°风向为例，分别对馈源舱无凸起和有凸起模型进行CFD仿真。计算风速取为2.7 m/s，时间步长取0.1 s，进行200 s的流场瞬态计算。经过计算可知，160 s后的计算结果均已稳定且收敛，因此选取160 s~200 s的数据进行分析，得到两种馈源舱结构模型的六分力系数均值如表4所示，表中气动力系数均取160 s~200 s内的时均值。可以比较看出两种馈源舱结构模型的气动力系数均值存在较大偏差，无凸起模型的C_d系数均值小于有凸起模型的，这是因为相较于有凸起模型，无凸起的馈源舱模型更接近于流线型设计，因此其阻力系数更小。考虑凸起后，升力系数由正值变为负值，由伯努利原理可知，流速越快压力越小，根据“等时理论”可知沿结构上下表面运动的气流将同时在结构后方汇合，由于无凸起模型上表面流线长度大于下表面，所以上表面的流速更快，上表面气压小于下表面气压，此时升力系数为正数，即升力方向竖直向上；但当模型上表面存在凸起后，凸起部分会阻碍气体的流动，导致其流速变慢，从而使上表面气压大于下表面气压，此时升力系数变为负数，即升力方向竖直向下。综上说明凸起部分对馈源舱结构气动力特性有显著影响，在开展CFD仿真时应该加以考虑。

表 4 两种馈源舱模型的气动力系数均值

Table 4. Average aerodynamic coefficients of two feed cabin models

气动力系数	无凸起模型	有凸起模型
阻力系数C_d	0.1743	0.2268
升力系数C_l	0.2929	−0.0550
侧向力系数C_Fz	−0.0071	−0.0119
倾覆力矩系数C_Mx	−0.0172	0.0068
偏航力矩系数C_My	0.0090	−0.0002
点头力矩系数C_Mz	0.0422	0.0013

下载: 导出CSV

| 显示表格

两个模型的阻力系数和升力系数时程曲线如图7所示，无凸起模型的C_d系数和C_l系数约在35 s后趋于稳定，有凸起模型的C_d系数和C_l系数约在80 s后趋于稳定，稳定后时程曲线整体呈现周期性波动，而无凸起模型则无此现象，进一步说明两者间存在巨大气动力差异。

两个模型在竖向剖面的速度分布云图如图8所示，可以直观的看出两者速度分布云图完全不同，相较于无凸起模型，有凸起模型的流场分布更为复杂。上述结果表明凸起对馈源舱结构的气动力特性有极大影响，因此在进行CFD仿真时非常有必要考虑馈源舱结构的凸起部分。

图 7 气动力系数时程曲线

Figure 7. Time-history curves of aerodynamic coefficients

下载: 全尺寸图片幻灯片

图 8 两种馈源舱模型速度分布云图(200 s)

Figure 8. Vertical velocity distribution of the two feed cabins

下载: 全尺寸图片幻灯片

2.2 不同风向工况下馈源舱模型气动力特性

对馈源舱结构凸起模型进行CFD精细化仿真，取6个风向工况进行计算，分别为0°、60°、120°、180°、240°和300°风向，具体定义详见图4。计算风速取2.7 m/s，时间步长取0.1 s，进行200 s的流场瞬态计算，确保计算结果稳定。

经过计算可知，160 s后的计算结果均已稳定且收敛，因此选取160 s~200 s的数据进行处理分析，得到六种风向工况下馈源舱凸起模型的六分力系数均值如表5所示，表中气动力系数均取160 s~200 s内的时均值。从表5中可知，C_d系数均值在风向角为240°时最大，在风向角为180°时最小，最大值与最小值的比值约为1.3，相对变化较小；C_l系数均值的绝对值在风向角为240°时最大，在风向角为300°时最小，最大值与最小值的比值约为4.6，相对变化较大；C_Fz、C_Mx、C_My和C_Mz系数均值的大小会随着风向的改变而发生变化，但整体数值偏小，对结构动力响应贡献有限。

表 5 各风向工况下馈源舱模型的气动力系数均值

Table 5. Average aerodynamic coefficients of feed cabin model under various wind directions

风向/(°)	阻力系数C_d	升力系数C_l	侧向力系数C_Fz	倾覆力矩系数C_Mx	偏航力矩系数C_My	点头力矩系数C_Mz
0	0.2396	−0.1067	−0.0047	−0.0021	0.0010	0.0033
60	0.2699	−0.1451	0.0701	−0.0200	0.0031	0.0147
120	0.2675	−0.1338	−0.0258	0.0086	−0.0041	0.0145
180	0.2268	−0.0550	−0.0119	0.0068	−0.0002	0.0013
240	0.2947	−0.1998	0.0342	−0.0128	0.0050	0.0238
300	0.2484	−0.0438	−0.0527	0.0108	−0.0037	0.0037

下载: 导出CSV

| 显示表格

不同风向下，馈源舱凸起模型C_d系数和C_l系数最后40 s时程曲线如图9所示。各风向下的C_d系数和C_l系数在其稳定后均有一定幅度的波动，其中180°和300°风向，C_d系数和C_l系数稳定后的波动具有明显的周期性；240°风向是气动力系数最大的风向。

图 9 各风向下馈源舱模型气动力系数时程曲线

Figure 9. Time history curves of aerodynamic coefficients of the feed cabin model under various wind directions

下载: 全尺寸图片幻灯片

对180°和300°风向作用下馈源舱模型的C_d系数和C_l系数在160 s~200 s内的数据进行快速傅里叶变换(Fast Fourier Transformation，FFT)，结果如图10所示。两个风向下的C_d系数和C_l系数频响曲线具有明显的单峰，180°风向和300°风向的频响曲线峰值对应的主频分别为为0.3 Hz和0.2 Hz。

图 10 各风向工况下馈源舱模型气动力系数频响曲线

Figure 10. Frequency response curves of aerodynamic coefficients of feed cabin model under various wind directions

下载: 全尺寸图片幻灯片

为进一步确认180°和300°风向工况是否发生涡激振动^[21-24]，提取两风向工况的速度分布云图和涡量分布云图，如图11和图12所示。结合涡量分布云图和速度分布云图可知，180°风向作用下结构附近流场有明显的旋涡脱落，说明馈源舱极易发生涡激振动，图11中标注了旋涡脱落的位置，位于馈源舱后侧的凸起处，通过频响曲线可知旋涡脱落的频率为0.3 Hz；300°风向涡量分布云图中无旋涡脱落现象，虽然其频响曲线有明显的主频，但该工况不会发生涡激振动。其余风向作用下，结构附近流场均无旋涡脱落现象。

图 11 180°风向速度和涡量分布云图(200 s)

Figure 11. The cloud charts of velocity and vorticity distribution under 180 degree wind direction

下载: 全尺寸图片幻灯片

图 12 300°风向速度和涡量分布云图(200 s)

Figure 12. The cloud charts of velocity and vorticity distribution under 300 degree wind direction

下载: 全尺寸图片幻灯片

2.3 风速影响分析及斯托罗函数计算

针对180°风向进行风速影响分析，取六个风速工况进行参数分析。FAST为洼地台址，由于周围山体的遮蔽，FAST现场风速非常小，根据国家天文台提供的馈源舱风速分析报告可知，馈源舱的最大风速值不到6 m/s，因此工况1~工况6对应的计算风速取为0.7 m/s、1.7 m/s、2.7 m/s、3.7 m/s、4.7 m/s和5.7 m/s，计算时间步长取0.1 s，为确保计算结果稳定，对0.7 m/s和1.7 m/s风速工况进行400 s的流场瞬态计算，对其他风速工况进行200 s的流场瞬态计算。

经过计算可知，各风速工况最后40 s的计算结果均已稳定且收敛，因此都选取最后40 s内的计算数据进行处理分析，得到六种风速工况下馈源舱凸起模型的六分力系数均值如表6所示，表中气动力系数均取最后40 s内的时均值。从表中可知，C_d系数均值在风速为0.7 m/s时最大，在风速为5.7 m/s时最小，最大值与最小值的比值约为1.14，相对变化较小；C_l系数均值的绝对值在风速为5.7 m/s时最大，在风速为1.7 m/s时最小，最大值与最小值的比值约为5.96，相对变化较大；C_Fz、C_Mx、C_My和C_Mz系数均值的大小会随着风速的改变而发生变化，但整体数值偏小。

表 6 各风速工况下馈源舱模型的气动力系数均值

Table 6. Average aerodynamic coefficients of feed cabin model under various wind speeds

风速/ (m/s)	阻力系数C_d	升力系数C_l	侧向力系数C_Fz	倾覆力矩系数C_Mx	偏航力矩系数C_My	点头力矩系数C_Mz
0.7	0.2406	−0.0525	0.0031	0.0038	0.0008	0.0046
1.7	0.2296	−0.0474	−0.0141	0.0073	−0.0002	0.0026
2.7	0.2268	−0.0550	−0.0119	0.0068	−0.0002	0.0013
3.7	0.2351	−0.1231	−0.0258	0.0051	−0.0018	−0.0041
4.7	0.2132	−0.2787	−0.0368	0.0125	−0.0023	−0.0206
5.7	0.2117	−0.2825	−0.0343	0.0100	−0.0023	−0.0213

下载: 导出CSV

| 显示表格

不同风速工况下，馈源舱凸起模型的C_d系数和C_l系数的最后40 s时程曲线如图13所示。其中0.7 m/s风速工况下的C_d系数和C_l系数稳定后无明显周期性波动，其他风速工况下的C_d系数和C_l系数稳定后的波动均具有明显的周期性。

各风速工况下阻力系数脉动均方根C_drms和升力系数脉动均方根C_lrms如表7所示。从表中可知，各风速工况下的C_drms和C_lrms都非常小，由于系数脉动均方根过小，实际工程中可能很难观测到180°风向的涡激振动现象。

图 13 各风速工况下馈源舱模型气动力系数时程曲线

Figure 13. Time history curves of aerodynamic coefficients of the feed cabin model under various wind speeds

下载: 全尺寸图片幻灯片

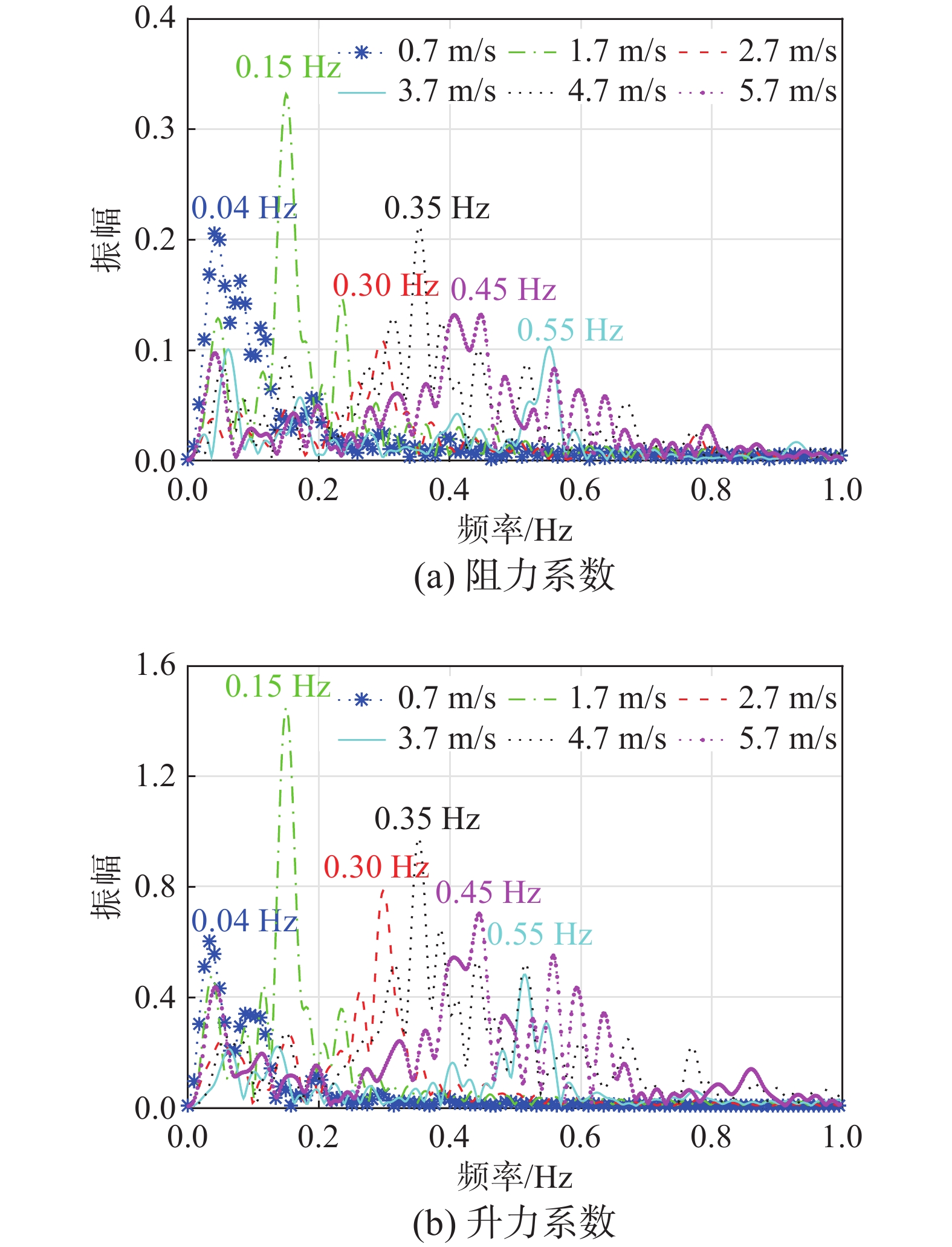
表 7 各风速工况下气动力系数脉动均方根

Table 7. Root mean square of aerodynamic coefficient fluctuation under various wind speeds

风速/(m/s)	阻力系数脉动均方根C_drms	升力系数脉动均方根C_lrms
0.7	0.0011	0.0029
1.7	0.0014	0.0059
2.7	0.0006	0.0036
3.7	0.0006	0.0024
4.7	0.0012	0.0057
5.7	0.0010	0.0051

下载: 导出CSV

| 显示表格

对不同风速下馈源舱模型的C_d系数和C_l系数进行FFT分析，结果如图14所示。从图14中可知，C_l系数频响曲线峰值大于C_d系数频响曲线峰值，C_l系数对结构的旋涡脱落影响更大，因此C_l系数频响曲线对应的主频即为旋涡脱落的频率f_v，工况1~工况6对应的旋涡脱落频率分别为0.04 Hz、0.15 Hz、0.30 Hz、0.52 Hz、0.35 Hz和0.45 Hz。

已知馈源舱模型风速和对应旋涡脱落频率时，即可采用下式计算馈源舱模型的斯托罗函数^[25]：

$St = \frac{{{f_{\rm{s}}}D}}{U}$

(3)

式中：f_s为结构发生涡激振动的旋涡脱落频率，可取f_v；D为馈源舱的特征长度，可取竖直方向的平均尺寸，约为3.07 m；U为结构的来流风速。

图 14 各风速工况下馈源舱模型气动力系数频响曲线

Figure 14. Frequency response curves of aerodynamic coefficients of feed cabin model under various wind speeds

下载: 全尺寸图片幻灯片

不同工况下馈源舱模型斯托罗函数如图15所示。斯托罗函数St先随着风速的增大线性增加，风速超过3.7 m/s后斯托罗函数骤降，之后又随着风速的增大逐渐增加，但增幅明显降低。

图 15 各风速工况下的馈源舱模型斯托罗函数

Figure 15. Strouhal numbers of the feed cabin model under various wind speeds

下载: 全尺寸图片幻灯片

3 馈源舱-索塔耦联体系振动特性

3.1 有限元模型及模态分析

采用ANSYS软件建立馈源舱-索塔耦联体系仿真模型，六个支撑塔在直径600 m的圆周上均匀布置，各支撑塔塔顶高度相同，由于山体地势有高差，支撑塔塔高为130 m~180 m。拉索直径为0.046 m，馈源舱外径尺寸约为13 m，高度为4.19 m，馈源舱与支撑塔塔顶高差为130 m。馈源舱受力构件采用Q345钢材，支撑塔材料主要采用Q235钢和Q345钢，拉索选用型号为Casar Super Plast 8的46 mm直径钢丝绳。在软件中采用Beam188单元模拟馈源舱受力构件和支撑塔结构，根据馈源舱结构的设计图纸，对馈源舱受力框架进行精细化建模，采用Link180单元模拟六根拉索，根据拉索两侧固定点位置及悬链线方程得到初始形状^[26]。结构阻尼比取0.02，采用Rayleigh阻尼并在软件中通过定义各材料阻尼参数实现。建立的有限元模型如图16所示。

图 16 有限元模型

Figure 16. Finite element model

下载: 全尺寸图片幻灯片

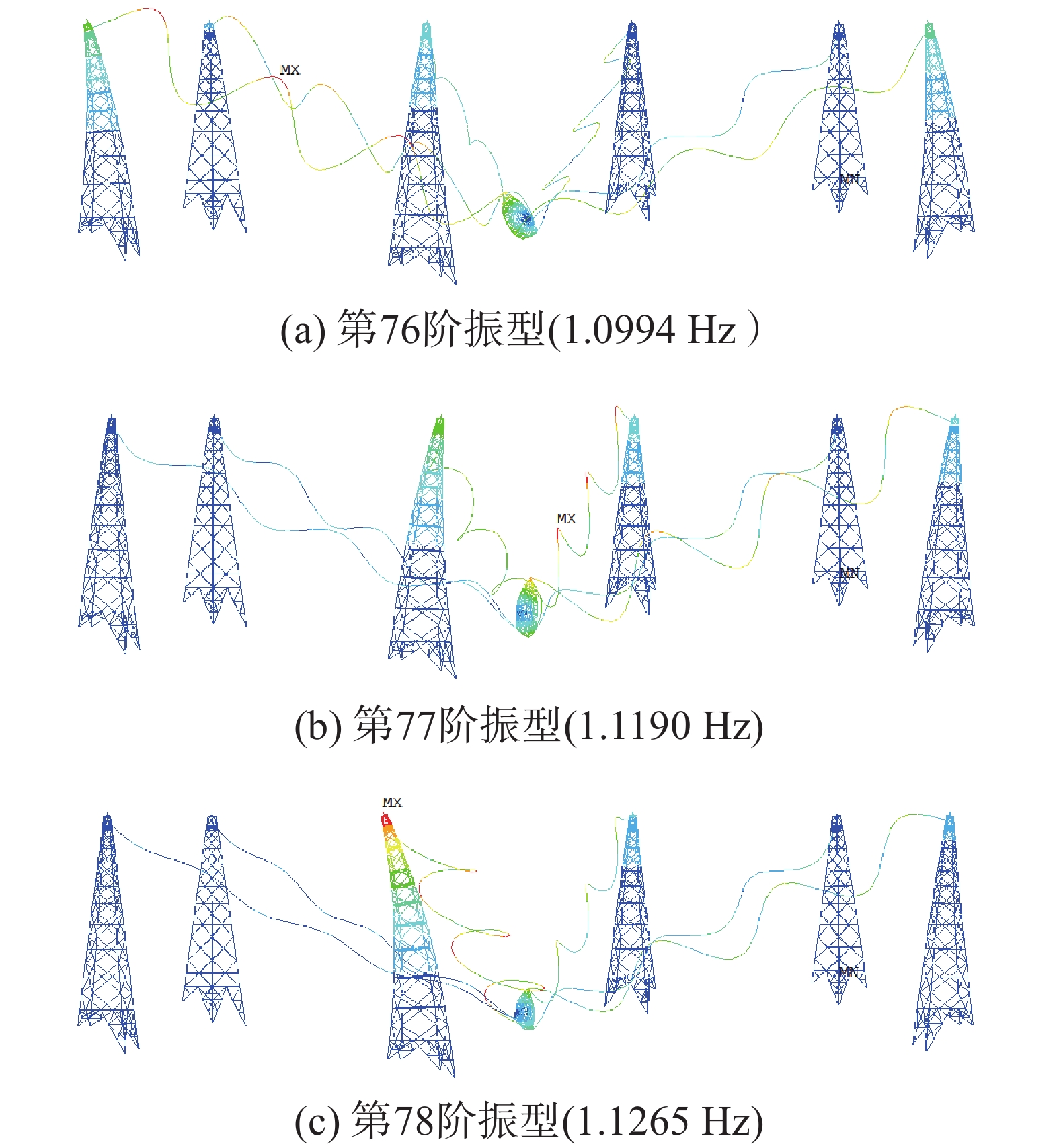
为获取结构的振动频率，开展大变形下馈源舱-索塔耦联体系的自重分析，进而开展模态分析。提取前12阶振型的频率如表8所示。从表8中可明显看出，结构的基频很小，且模态密集，在常遇风速内可依次激发结构的多阶模态，也即可激发基频以上的结构高阶模态振动。

表 8 模态频率

Table 8. Modal frequency

振型阶次	频率/Hz	振型阶次	频率/Hz
1	0.1475	7	0.1751
2	0.1478	8	0.1754
3	0.1682	9	0.1774
4	0.1717	10	0.2151
5	0.1718	11	0.3053
6	0.1719	12	0.3057

下载: 导出CSV

| 显示表格

馈源舱-索塔耦联体系为超大空间结构，风荷载是结构设计的控制性荷载。通过前述气动力分析结果可知，240°是气动力系数最大的风向，180°是潜在涡激振动的风向，但由于180°风向工况的阻力系数和升力系数脉动均方根过小，实际工程中很难观测到涡激振动现象，因此对该风向进行风振响应分析的意义较小。本文后续针对前述气动力分析中系数最大的240°风向进行风振响应研究。

3.2 支撑塔对模态结果的影响

建立无支撑塔的馈源舱-索耦联体系，按照如上方法进行模态分析。为对比有无支撑塔对整个结构体系振型和频率的影响，图17和图18为有无支撑塔模型的第76阶~第78阶模态，从振型图中可以看出支撑塔对结构体系的振型影响较小，但考虑支撑塔后自振频率会明显降低，这主要是由于固定约束刚度无限大，而支撑塔的刚度是一有限数值，因此支撑塔和拉索及馈源舱耦联后自振频率显著降低。结构自振频率的改变必然会影响结构体系的动力响应，因此建模中有必要考虑支撑塔。

图 17 有支撑塔模型模态振型和频率

Figure 17. Modal shape and frequency of supported tower model

下载: 全尺寸图片幻灯片

图 18 无支撑塔模型模态振型和频率

Figure 18. Modal shape and frequency of unsupported tower model

下载: 全尺寸图片幻灯片

4 耦联体系风振响应分析

4.1 风场模拟

本文采用指数风剖面模拟平均风速，选取Davenport谱^[27]进行脉动风速模拟，表达式如下：

${S_V}(f) = 4K{V_{{10}}^2}\frac{{{x^2}}}{{f{{(1 + {x^2})}^{4/3}}}}$

(4)

$x = 1200\frac{f}{{{V_{10}}}}$

(5)

式中：K为地表阻力系数；f为脉动频率；V₁₀为基本风速。

不同位置脉动风速的相干函数采用频率和两点间距相关的指数函数表示，相干函数模型表达式如下：

$\begin{split} & {\text{coh}}(f,\Delta x,\Delta y,\Delta {\textit{z}}) = \\ &\qquad \exp \left( { - \frac{{2f\sqrt {C_x^2\Delta {x^2} + C_y^2\Delta {y^2} + C_{\textit{z}}^2\Delta {{\textit{z}}^2}} }}{{{V_i} + {V_j}}}} \right) \end{split}$

(6)

式中：Δx、Δy和Δz分别表示任意两点处的横向、纵向和垂直距离；衰减系数C_x、C_y和C_z需根据现场测量确定，SIMIU和YEO^[28]建议C_x、C_y、C_z分别取16、6、10，本文采用该推荐值；V_i和V_j分别表示i、j两点的平均风速。

采用谐波叠加法模拟脉动风速时程。脉动风速的互谱密度矩阵S(f)表达式如下：

$S(f) = \left[ {\begin{array}{*{20}{c}} {{S_{11}}(f)}&{{S_{12}}(f)}& \ldots &{{S_{1n}}(f)} \\ {{S_{21}}(f)}&{{S_{22}}(f)}& \ldots &{{S_{2n}}(n)} \\ \ldots & \ldots & \ldots & \ldots \\ {{S_{n1}}(f)}&{{S_{n2}}(f)}& \ldots &{{S_{nn}}(f)} \end{array}} \right]$

(7)

式中，任一元素S_ij(f)为两点间的互谱密度，表达式如下：

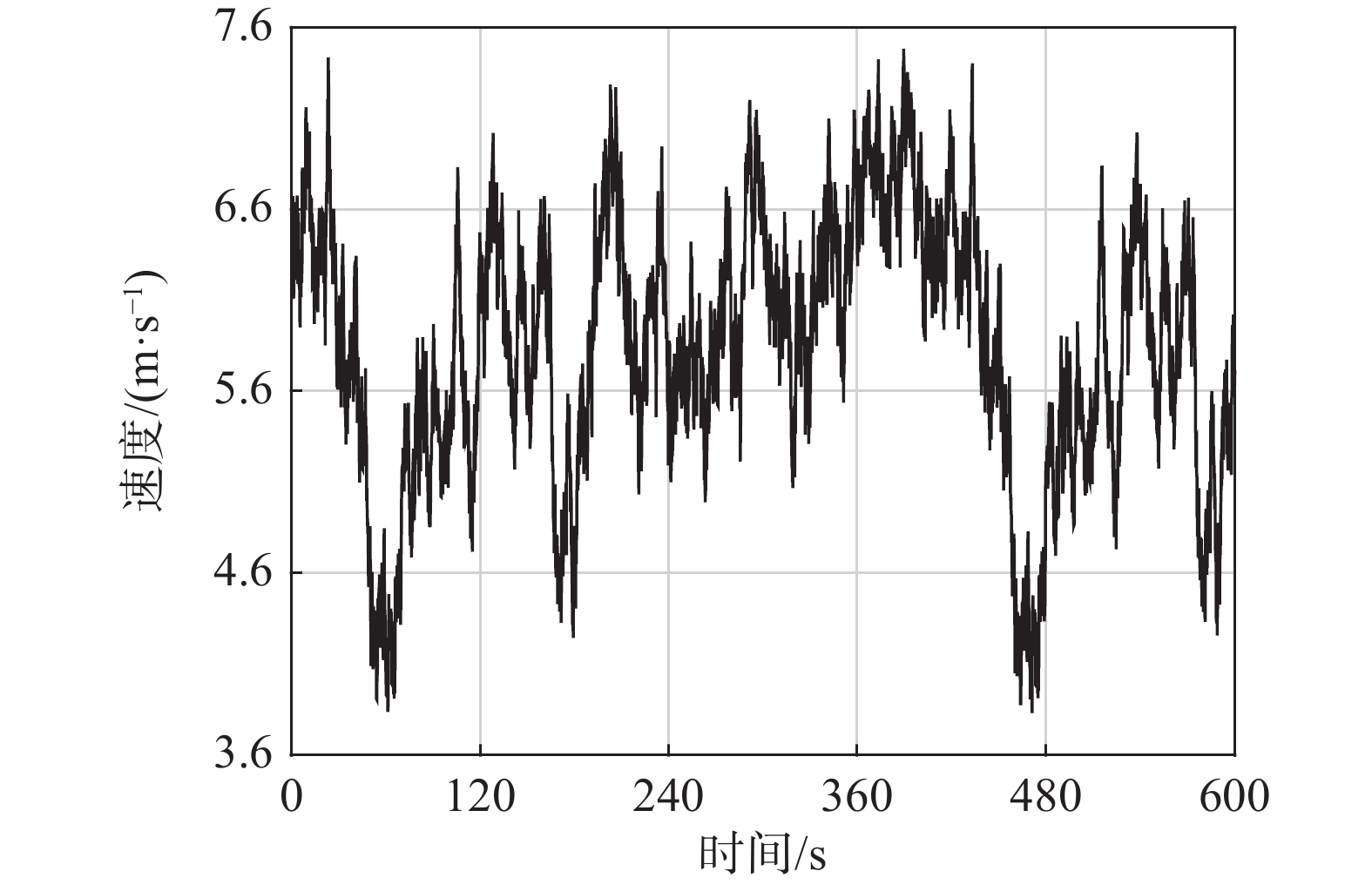
${S_{ij}}(f) = {S_V}(f){\text{coh(}}f,\Delta x,\Delta y,\Delta {\textit{z}})$

(8)

生成脉动风速的具体参数如下：1)地面粗糙度类别为B类；2)总时间为600 s，时间步长为0.1 s；3)截止频率为5 Hz，频率等分数为1024；4)以FAST索网结构最低点为0高度点，取两组基本风速，分别为4 m/s(工作风速)和14 m/s(设计风速)；5)风向为南偏东44度方向(对应馈源舱气动力系数最大的240度风向)。工作风速工况下馈源舱中心点的脉动风速时程如图19所示。

图 19 模拟的脉动风速

Figure 19. Simulated fluctuating wind speed

下载: 全尺寸图片幻灯片

为验证本文模拟方法是否有效可靠，应对模拟脉动风的功率谱与Davenport谱进行比较，如图20所示。从图20中可以看出，模拟风谱的总体趋势与Davenport谱是一致的，说明本次模拟采用的脉动风生成方法及编程是合理有效的。

图 20 风谱对比

Figure 20. The comparison of wind spectra

下载: 全尺寸图片幻灯片

4.2 风荷载计算

本文将馈源舱简化为一个风荷载加载点，通过上述CFD模拟方法获得对应工况的馈源舱结构气动力系数。将每根拉索等间距地简化为30个风荷载加载点，支撑塔结构根据高度简化为10到14个风荷载加载点，如图21所示。

风荷载可根据下式进行计算：

${F_{\rm{a}}}(t) = {\mu _{\rm{s}}}A\rho {v^2}(t)\eta /2$

(9)

式中：v(t)为总风速，等于平均风加脉动风；ρ为空气密度，取值1.225 kg/m³；风荷载体形系数μ_s根据规范进行选取，拉索体型系数取1.0，各支撑塔体型系数取1.56^[29]；A表示结构的受风投影面积；η为地形修正系数，根据规范可在0.75~0.85选取，本文取0.8。

馈源舱-索塔耦联体系总计250个风荷载加载点，提取坐标点，确定风向与风速，进而将荷载序列施加在有限元模型上，开展馈源舱-索塔耦联体系的动力时程分析。

图 21 风荷载加载点

Figure 21. Loading point of wind load

下载: 全尺寸图片幻灯片

4.3 风振响应分析

FAST系统需达到六根柔索驱动馈源舱在空间各方向≤48 mm定位精度、姿态角误差≤1°的控制要求，否则会影响馈源舱的工作精度。4 m/s风速工况下馈源舱结构中心点的最大平动位移和最大姿态角如表9所示，其中平动位移取偏移后的馈源舱位置与原位置的直线距离，翻滚角、俯仰角和偏航角分别对应纵向、横向和竖向转动角度。从表中可知，工作风速下馈源舱最大平动位移约为8.7 mm，最大姿态角的绝对值远小于1°，故而在工作风速下，不会影响馈源舱的正常工作。

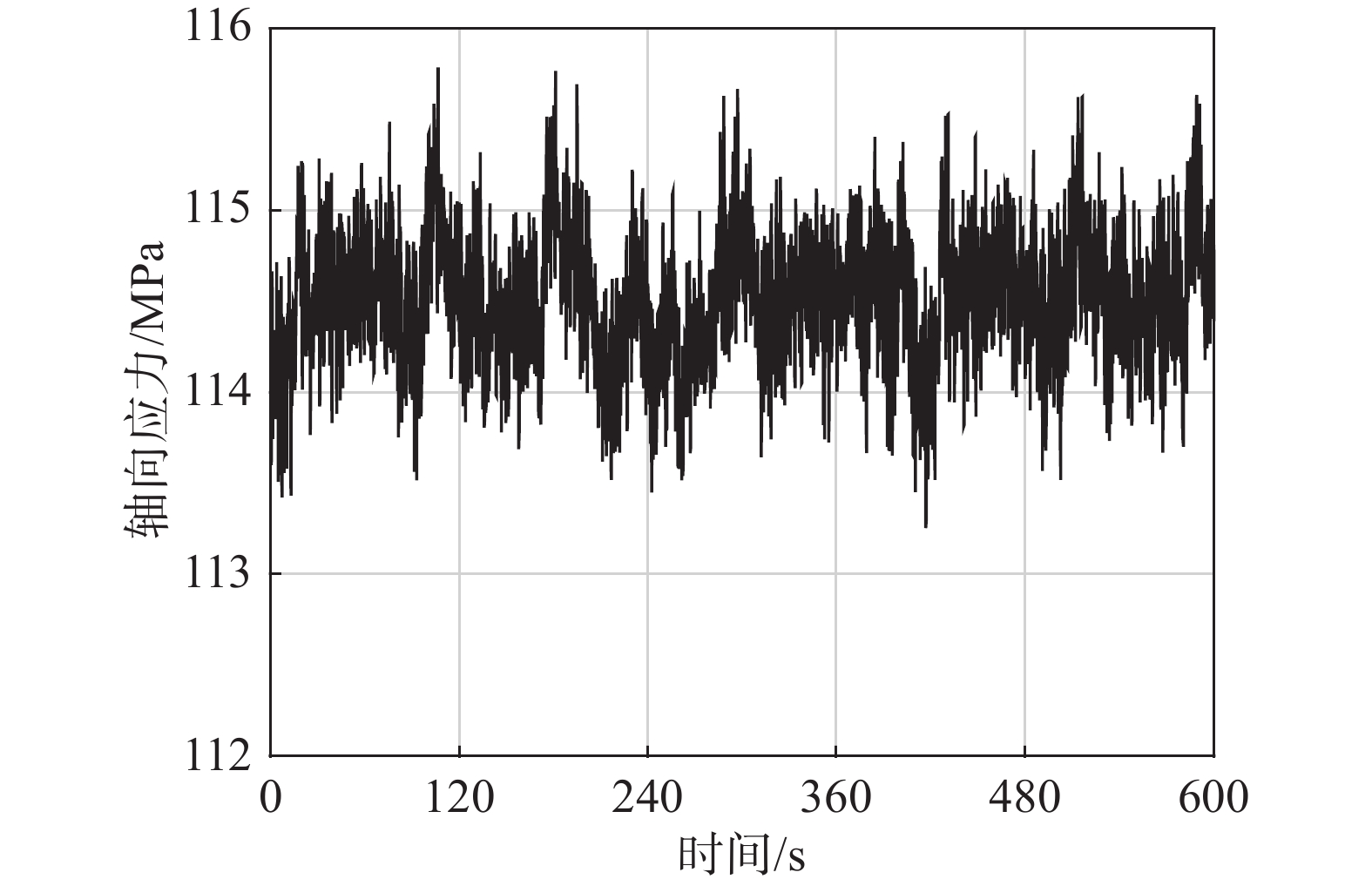
表 9 工作风速下馈源舱最大响应

Table 9. Maximum response of the feed cabin under working wind speed

平动位移/mm	翻滚角/(°)	俯仰角/(°)	偏航角/(°)
8.7	0.0091	−0.0240	−0.0158

下载: 导出CSV

| 显示表格

为了保证FAST系统的安全性，需要校核各个组成结构在设计风速下的强度。馈源舱受力构件材料采用Q345钢，支撑塔材料主要采用Q235钢和Q345钢，Q235钢是支撑塔的辅助结构材料，结构应力很小，本文暂不考虑其安全问题，Q345钢的屈服强度为345 MPa，设计风速下馈源舱和支撑塔的最大受力杆件的应力时程曲线如图22所示。图中可知设计风速下馈源舱的最大应力约为80.7 MPa、支撑塔的最大应力约为57.8 MPa，都远小于材料的屈服强度，结构安全。拉索选用型号为Casar Super Plast 8的46 mm直径钢丝绳，抗拉强度为1960 MPa^[30]，设计风速下拉索的最大轴向应力时程曲线如图23所示，最大轴向应力约为116 MPa，远小于材料的抗拉强度，结构安全。

图 22 馈源舱和支撑塔的最大应力时程曲线

Figure 22. Time history curve of maximum stress of the feed cabin and support towers

下载: 全尺寸图片幻灯片

图 23 拉索最大轴向应力时程曲线

Figure 23. Time history curve of maximum axial stress for the steel cables

下载: 全尺寸图片幻灯片

六索控制是馈源舱的一次调整平台，需达到六根拉索驱动馈源舱在空间各方向≤48 mm定位精度、姿态角误差≤1°的控制要求。馈源舱内部有Stewart平台精调系统，主要为了减少和抑制整个馈源舱的风振响应，该系统是馈源舱的二次精调平台，FAST验收要求是中心点的位置精度RMS不大于10 mm。本文未考虑馈源舱的二次精调平台，默认其关闭，计算了馈源舱-索塔耦联体系满足一次、二次精调平台精度的最大工作风速，分别为9.3 m/s和4.3 m/s。结果表明，若开启二次精调平台，最大工作风速可以达到9.3 m/s；当风速小于4.3 m/s时，即使不打开二次精调平台，也满足工作精度要求。

5 结论

本文研究了馈源舱结构的气动力特性，并揭示了其涡激振动的产生机制和发生工况；基于ANSYS软件，模拟了馈源舱-索塔耦联体系在工作风速和设计风速下的动力响应，对其安全性进行了全面校核，得到的主要结论如下：

(1) 分别建立了表面无凸起和有凸起的馈源舱CFD仿真模型，证明了表面凸起部分对馈源舱结构的气动力特性有极大影响；发现了240°风向是气动力系数最大的风向，180°为潜在涡激振动的风向，旋涡脱落位置在结构表面凸起处，并针对180°风向进行参数分析，得到了模型在不同风速下的旋涡脱落频率和斯托罗函数。建议避免结构表面有凸起部分，保证馈源舱为流线型，预防涡激振动的发生。

(2) 馈源舱-索塔耦联体系的模态非常密集，常遇风速内可依次激发结构的多个模态，即可激发基频以上的结构高阶模态振动。

(3) 针对气动力系数最大的240°风向进行风振响应分析，得到馈源舱在工作风速下的最大平动位移为8.7 mm，最大姿态角的绝对值远小于1°，说明在4 m/s风速下不会影响馈源舱的正常工作；设计风速下的应力结果远小于材料极限强度，说明结构安全可靠。

(4) 若开启二次精调平台，最大工作风速可以达到9.3 m/s；当风速小于4.3 m/s时，即使不打开二次精调平台，也满足工作精度要求。最大工作风速建议值可为FAST工程运行观测及抗风设计提供参考。

图 1 馈源舱结构实拍图

Figure 1. Picture of the feed cabin structure

下载: 全尺寸图片幻灯片

图 2 馈源舱CFD仿真模型

Figure 2. CFD simulation model of the feed cabin

下载: 全尺寸图片幻灯片

图 3 计算域示意图　/m

Figure 3. Schematic of the computational domain

下载: 全尺寸图片幻灯片

图 4 风向角定义

Figure 4. Definition of wind direction

下载: 全尺寸图片幻灯片

图 5 六分力示意图

Figure 5. Schematic of six-component force

下载: 全尺寸图片幻灯片

图 6 馈源舱模型混合网格

Figure 6. Mixed grids of the feed cabin model

下载: 全尺寸图片幻灯片

图 7 气动力系数时程曲线

Figure 7. Time-history curves of aerodynamic coefficients

下载: 全尺寸图片幻灯片

图 8 两种馈源舱模型速度分布云图(200 s)

Figure 8. Vertical velocity distribution of the two feed cabins

下载: 全尺寸图片幻灯片

图 9 各风向下馈源舱模型气动力系数时程曲线

Figure 9. Time history curves of aerodynamic coefficients of the feed cabin model under various wind directions

下载: 全尺寸图片幻灯片

图 10 各风向工况下馈源舱模型气动力系数频响曲线

Figure 10. Frequency response curves of aerodynamic coefficients of feed cabin model under various wind directions

下载: 全尺寸图片幻灯片

图 11 180°风向速度和涡量分布云图(200 s)

Figure 11. The cloud charts of velocity and vorticity distribution under 180 degree wind direction

下载: 全尺寸图片幻灯片

图 12 300°风向速度和涡量分布云图(200 s)

Figure 12. The cloud charts of velocity and vorticity distribution under 300 degree wind direction

下载: 全尺寸图片幻灯片

图 13 各风速工况下馈源舱模型气动力系数时程曲线

Figure 13. Time history curves of aerodynamic coefficients of the feed cabin model under various wind speeds

下载: 全尺寸图片幻灯片

图 14 各风速工况下馈源舱模型气动力系数频响曲线

Figure 14. Frequency response curves of aerodynamic coefficients of feed cabin model under various wind speeds

下载: 全尺寸图片幻灯片

图 15 各风速工况下的馈源舱模型斯托罗函数

Figure 15. Strouhal numbers of the feed cabin model under various wind speeds

下载: 全尺寸图片幻灯片

图 16 有限元模型

Figure 16. Finite element model

下载: 全尺寸图片幻灯片

图 17 有支撑塔模型模态振型和频率

Figure 17. Modal shape and frequency of supported tower model

下载: 全尺寸图片幻灯片

图 18 无支撑塔模型模态振型和频率

Figure 18. Modal shape and frequency of unsupported tower model

下载: 全尺寸图片幻灯片

图 19 模拟的脉动风速

Figure 19. Simulated fluctuating wind speed

下载: 全尺寸图片幻灯片

图 20 风谱对比

Figure 20. The comparison of wind spectra

下载: 全尺寸图片幻灯片

图 21 风荷载加载点

Figure 21. Loading point of wind load

下载: 全尺寸图片幻灯片

图 22 馈源舱和支撑塔的最大应力时程曲线

Figure 22. Time history curve of maximum stress of the feed cabin and support towers

下载: 全尺寸图片幻灯片

图 23 拉索最大轴向应力时程曲线

Figure 23. Time history curve of maximum axial stress for the steel cables

下载: 全尺寸图片幻灯片

表 1 各网格方案气动力系数均值

Table 1 Average aerodynamic coefficients of each grid scheme

网格方案	网格数量	阻力系数C_d	升力系数C_l	侧向力系数C_Fz	倾覆力矩系数C_Mx	偏航力矩系数C_My	点头力矩系数C_Mz
M1	337万	0.2268	−0.0550	−0.0119	0.0068	−0.0002	0.0013
M2	608万	0.2316	−0.0587	−0.0189	0.0027	−0.0019	0.0005
M3	583万	0.2274	−0.0536	−0.0087	0.0069	−0.0002	0.0013
M4	114万	0.2299	−0.1285	0.0116	0.0022	0.0010	−0.0048

下载: 导出CSV

表 2 各网格方案脉动均方根

Table 2 Pulsating root mean square of each grid scheme

网格方案	阻力系数脉动均方根C_drms	升力系数脉动均方根C_lrms
M1	0.0006	0.0036
M2	0.0007	0.0039
M3	0.0005	0.0034
M4	0.0001	0.0006

下载: 导出CSV

表 3 各时间步长算例气动力系数

Table 3 Aerodynamic coefficients of various time steps

时间步长/s	阻力系数 C_d	升力系数 C_l	阻力系数脉动均方根C_drms	升力系数脉动均方根C_lrms
0.10	0.2268	−0.0550	0.0006	0.0036
0.05	0.2267	−0.0543	0.0006	0.0036
0.02	0.2264	−0.0540	0.0007	0.0035

下载: 导出CSV

表 4 两种馈源舱模型的气动力系数均值

Table 4 Average aerodynamic coefficients of two feed cabin models

气动力系数	无凸起模型	有凸起模型
阻力系数C_d	0.1743	0.2268
升力系数C_l	0.2929	−0.0550
侧向力系数C_Fz	−0.0071	−0.0119
倾覆力矩系数C_Mx	−0.0172	0.0068
偏航力矩系数C_My	0.0090	−0.0002
点头力矩系数C_Mz	0.0422	0.0013

下载: 导出CSV

表 5 各风向工况下馈源舱模型的气动力系数均值

Table 5 Average aerodynamic coefficients of feed cabin model under various wind directions

风向/(°)	阻力系数C_d	升力系数C_l	侧向力系数C_Fz	倾覆力矩系数C_Mx	偏航力矩系数C_My	点头力矩系数C_Mz
0	0.2396	−0.1067	−0.0047	−0.0021	0.0010	0.0033
60	0.2699	−0.1451	0.0701	−0.0200	0.0031	0.0147
120	0.2675	−0.1338	−0.0258	0.0086	−0.0041	0.0145
180	0.2268	−0.0550	−0.0119	0.0068	−0.0002	0.0013
240	0.2947	−0.1998	0.0342	−0.0128	0.0050	0.0238
300	0.2484	−0.0438	−0.0527	0.0108	−0.0037	0.0037

下载: 导出CSV

表 6 各风速工况下馈源舱模型的气动力系数均值

Table 6 Average aerodynamic coefficients of feed cabin model under various wind speeds

风速/ (m/s)	阻力系数C_d	升力系数C_l	侧向力系数C_Fz	倾覆力矩系数C_Mx	偏航力矩系数C_My	点头力矩系数C_Mz
0.7	0.2406	−0.0525	0.0031	0.0038	0.0008	0.0046
1.7	0.2296	−0.0474	−0.0141	0.0073	−0.0002	0.0026
2.7	0.2268	−0.0550	−0.0119	0.0068	−0.0002	0.0013
3.7	0.2351	−0.1231	−0.0258	0.0051	−0.0018	−0.0041
4.7	0.2132	−0.2787	−0.0368	0.0125	−0.0023	−0.0206
5.7	0.2117	−0.2825	−0.0343	0.0100	−0.0023	−0.0213

下载: 导出CSV

表 7 各风速工况下气动力系数脉动均方根

Table 7 Root mean square of aerodynamic coefficient fluctuation under various wind speeds

风速/(m/s)	阻力系数脉动均方根C_drms	升力系数脉动均方根C_lrms
0.7	0.0011	0.0029
1.7	0.0014	0.0059
2.7	0.0006	0.0036
3.7	0.0006	0.0024
4.7	0.0012	0.0057
5.7	0.0010	0.0051

下载: 导出CSV

表 8 模态频率

Table 8 Modal frequency

振型阶次	频率/Hz	振型阶次	频率/Hz
1	0.1475	7	0.1751
2	0.1478	8	0.1754
3	0.1682	9	0.1774
4	0.1717	10	0.2151
5	0.1718	11	0.3053
6	0.1719	12	0.3057

下载: 导出CSV

表 9 工作风速下馈源舱最大响应

Table 9 Maximum response of the feed cabin under working wind speed

平动位移/mm	翻滚角/(°)	俯仰角/(°)	偏航角/(°)
8.7	0.0091	−0.0240	−0.0158

下载: 导出CSV

参考文献(30)

[1]	JIANG P, YUE Y L, GAN H Q, et al. Commissioning progress of the FAST [J]. Science China Physics, Mechanics & Astronomy, 2019, 62(5): 959502.
[2]	JIANG P, LI Q W, NAN R D. Research on design of adaptive connecting mechanisms for the cable-net and panels of FAST [J]. Research in Astronomy and Astrophysics, 2017, 17(9): 099. doi: 10.1088/1674-4527/17/9/99
[3]	李辉, 朱文白, 潘高峰. FAST望远镜馈源支撑中的力学问题及其研究进展[J]. 力学进展, 2011, 41(2): 133 − 154. LI Hui, ZHU Wenbai, PAN Gaofeng. Mechanics in the feed support of FAST telescope and its research progress [J]. Advances in Mechanics, 2011, 41(2): 133 − 154. (in Chinese)
[4]	李玉学, 杨庆山, 田玉基, 等. 大跨屋盖结构多目标等效静力风荷载[J]. 工程力学, 2016, 33(6): 85 − 92. doi: 10.6052/j.issn.1000-4750.2014.10.0890 LI Yuxue, YANG Qingshan, TIAN Yuji, et al. Multiple targets equivalent static wind load for long-span roofs [J]. Engineering Mechanics, 2016, 33(6): 85 − 92. (in Chinese) doi: 10.6052/j.issn.1000-4750.2014.10.0890
[5]	吴迪, 武岳, 杨庆山, 等. 大跨屋盖结构风振响应参数灵敏度分析[J]. 工程力学, 2015, 32(2): 171 − 177. doi: 10.6052/j.issn.1000-4750.2013.09.0844 WU Di, WU Yue, YANG Qingshan, et al. Parameter sensitivity analysis of wind-induced response of long-span roofs [J]. Engineering Mechanics, 2015, 32(2): 171 − 177. (in Chinese) doi: 10.6052/j.issn.1000-4750.2013.09.0844
[6]	李玉学, 冯励睿, 李海云, 等. 大跨屋盖结构脉动风振响应特性预测方法研究[J]. 工程力学, 2021, 38(7): 159 − 166, 182. doi: 10.6052/j.issn.1000-4750.2020.07.0497 LI Yuxue, FENG Lirui, LI Haiyun, et al. A method for determining the characteristic of fluctuating wind-induced response of large-span roofs [J]. Engineering Mechanics, 2021, 38(7): 159 − 166, 182. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.07.0497
[7]	MA T T, ZHAO L, JI T F, et al. Case study of wind-induced performance and equivalent static wind loads of large-span openable truss structures [J]. Thin-Walled Structures, 2022, 175: 109206. doi: 10.1016/j.tws.2022.109206
[8]	吴明长, 王启明, 郭永卫, 等. 大射电望远镜FAST风环境数值模拟研究[J]. 天文研究与技术, 2012, 9(2): 121 − 128, 149. WU Mingchang, WANG Qiming, GUO Yongwei, et al. A numerical study on the wind environment of the FAST [J]. Astronomical Research & Technology, 2012, 9(2): 121 − 128, 149. (in Chinese)
[9]	段艳宾, 王迎发, 李建军, 等. FAST馈源舱系统动态特性联合仿真研究[J]. 机械设计与制造, 2014(8): 220 − 223. doi: 10.3969/j.issn.1001-3997.2014.08.068 DUAN Yanbin, WANG Yingfa, LI Jianjun, et al. Research on coordinated simulation of dynamic characteristics for the feed cabin of FAST [J]. Machinery Design & Manufacture, 2014(8): 220 − 223. (in Chinese) doi: 10.3969/j.issn.1001-3997.2014.08.068
[10]	魏书魁. 高空六索驱动并联机器人的风载分析[D]. 长春: 吉林大学, 2017. WEI Shukui. Wind loading analysis on six-driven parallel robot of high altitude [D]. Changchun: Jilin University, 2017. (in Chinese)
[11]	GB 50009−2012, 建筑结构荷载规范[S]. 北京: 中国建筑工业出版社, 2012. GB 50009−2012, Load code for the design of building structures [S]. Beijing: China Architecture & Building Press, 2012. (in Chinese)
[12]	卢旦, 李承铭, 王国俭. 上海金茂大厦风振响应的CFD非稳态数值模拟分析[J]. 土木工程学报, 2008, 41(8): 31 − 35. LU Dan, LI Chengming, WANG Guojian. CFD unsteady state numerical simulation of wind-induced vibration of the Shanghai Jinmao building [J]. China Civil Engineering Journal, 2008, 41(8): 31 − 35. (in Chinese)
[13]	顾磊, 齐宏拓, 刘红军, 等. 奥运网球中心赛场风荷载和风环境数值模拟分析[J]. 建筑结构学报, 2009, 30(3): 134 − 143. doi: 10.3321/j.issn:1000-6869.2009.03.017 GU Lei, QI Hongtuo, LIU Hongjun, et al. Numerical simulation on wind load characteristics and wind environment for Olympic park tennis centre stadium [J]. Journal of Building Structures, 2009, 30(3): 134 − 143. (in Chinese) doi: 10.3321/j.issn:1000-6869.2009.03.017
[14]	李艺, 黄国庆, 程旭, 等. 移动型下击暴流及其作用下高层建筑风荷载的数值模拟[J]. 工程力学, 2020, 37(3): 176 − 187. doi: 10.6052/j.issn.1000-4750.2019.04.0231 LI Yi, HUANG Guoqing, CHENG Xu, et al. The numerical simulation of moving downbursts and their induced wind load on high-rise buildings [J]. Engineering Mechanics, 2020, 37(3): 176 − 187. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.04.0231
[15]	杨庆山, 陈飞新, 赵乐, 等. 基于大涡模拟的大气边界层湍流强度对低矮房屋风荷载特性影响研究[J]. 工程力学, 2021, 38(12): 25 − 38. doi: 10.6052/j.issn.1000-4750.2020.10.0778 YANG Qingshan, CHEN Feixin, ZHAO Le, et al. Effects of upstream turbulence intensity on aerodynamic loads of low-rise buildings in atmospheric boundary layer flow using large eddy simulation [J]. Engineering Mechanics, 2021, 38(12): 25 − 38. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.10.0778
[16]	郑德乾, 柳阔, 全涌, 等. 杭州萧山国际机场T4航站楼主楼屋盖风荷载的风洞试验与数值模拟研究[J]. 建筑结构, 2021, 51(23): 28 − 33. doi: 10.19701/j.jzjg.2021.23.005 ZHENG Deqian, LIU Kuo, QUAN Yong, et al. Study on wind tunnel test and numerical simulation of wind load on the roof of Hangzhou Xiaoshan international airport T4 terminal building [J]. Building Structure, 2021, 51(23): 28 − 33. (in Chinese) doi: 10.19701/j.jzjg.2021.23.005
[17]	李建军, 窦玉超, 付强, 等. FAST馈源舱动力学设计及扰动抑制技术[J]. 电子机械工程, 2020, 36(6): 8 − 11, 15. LI Jianjun, DOU Yuchao, FU Qiang, et al. Kinetics design and disturbance rejection technique of FAST feed cabin [J]. Electro-Mechanical Engineering, 2020, 36(6): 8 − 11, 15. (in Chinese)
[18]	赵正旭, 刘曼云, 宋立强, 等. 射电望远镜馈源舱数字化模型的创建[J]. 现代计算机, 2019(26): 3 − 7, 12. doi: 10.3969/j.issn.1007-1423.2019.26.001 ZHAO Zhengxu, LIU Manyun, SONG Liqiang, et al. Creation of digital model of radio telescope’s feed cabin [J]. Modern Computer, 2019(26): 3 − 7, 12. (in Chinese) doi: 10.3969/j.issn.1007-1423.2019.26.001
[19]	MENTER F R. Zonal two equation k-ω turbulence models for aerodynamic flows [C]// 23rd Fluid Dynamics, Plasmadynamics, and Lasers Conference. Orlando: AIAA, 1993.
[20]	崔亮. 基于ANSYS FLUENT MESHING的复杂模型网格划分[J]. CAD/CAM与制造业信息化, 2014(4): 56 − 58. CUI Liang. Mesh generation of complex model based on ANSYS fluent meshing [J]. Digital Manufacturing Industry, 2014(4): 56 − 58. (in Chinese)
[21]	WILLIAMSON C H K, GOVARDHAN R. Vortex-induced vibrations [J]. Annual Review of Fluid Mechanics, 2004, 36: 413 − 455. doi: 10.1146/annurev.fluid.36.050802.122128
[22]	WILLIAMSON C H K, GOVARDHAN R. A brief review of recent results in vortex-induced vibrations [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(6/7): 713 − 735.
[23]	郭涛, 张纹惠, 王文全, 等. 基于IBM法的低雷诺数下涡激振动高质量比效应的研究[J]. 工程力学, 2022, 39(3): 222 − 232. doi: 10.6052/j.issn.1000-4750.2021.07.0566 GUO Tao, ZHANG Wenhui, WANG Wenquan, et al. Effects of high mass and damping ratio on VIV of a circular cylinder with low Reynolds number based on IBM [J]. Engineering Mechanics, 2022, 39(3): 222 − 232. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.07.0566
[24]	LIU B, JIANG R J. Vortex-induced vibrations of a rectangular cylinder [J]. Ocean Engineering, 2022, 266: 112883. doi: 10.1016/j.oceaneng.2022.112883
[25]	刘健新, 崔欣, 李加武. 桥梁断面表面压力分布及Strouhal数的雷诺数效应[J]. 振动与冲击, 2010, 29(4): 146 − 149. doi: 10.3969/j.issn.1000-3835.2010.04.033 LIU Jianxin, CUI Xin, LI Jiawu. Reynolds number effect of surface pressure distribution and Strouhal number of a typical bridge deck section [J]. Journal of Vibration and Shock, 2010, 29(4): 146 − 149. (in Chinese) doi: 10.3969/j.issn.1000-3835.2010.04.033
[26]	陈常松, 陈政清, 颜东煌. 悬索桥主缆初始位形的悬链线方程精细迭代分析法[J]. 工程力学, 2006, 23(8): 62 − 68. doi: 10.3969/j.issn.1000-4750.2006.08.012 CHEN Changsong, CHEN Zhengqing, YAN Donghuang. Accurate iteration method to calculate the initial states of main cables of suspension bridges [J]. Engineering Mechanics, 2006, 23(8): 62 − 68. (in Chinese) doi: 10.3969/j.issn.1000-4750.2006.08.012
[27]	DAVENPORT A G. The spectrum of horizontal gustiness near the ground in high winds [J]. Quarterly Journal of the Royal Meteorological Society, 1961, 87(372): 194 − 211. doi: 10.1002/qj.49708737208
[28]	SIMIU E, YEO D. Wind effects on structures: Modern structural design for wind, 4th edition[M]. West Sussex: John Wiley & Sons Ltd, 2019.
[29]	DL/T 5551−2018, 架空输电线路荷载规范[S]. 北京: 中国计划出版社, 2018. DL/T 5551−2018, Load code for the design of overhead transmission line [S]. Beijing: China Planning Press, 2018. (in Chinese)
[30]	李庆伟, 李辉, 姜鹏, 等. FAST馈源支撑钢索及舱索连接锚具役后剩余承载力研究[J]. 清华大学学报(自然科学版), 2022, 62(11): 1758 − 1763, 1779. doi: 10.16511/j.cnki.qhdxxb.2022.26.027 LI Qingwei, LI Hui, JIANG Peng, et al. Residual bearing capacity of the steel cables and anchorages of the FAST feed support system [J]. Journal of Tsinghua University (Science and Technology), 2022, 62(11): 1758 − 1763, 1779. (in Chinese) doi: 10.16511/j.cnki.qhdxxb.2022.26.027

施引文献

资源附件(0)

图(23) / 表(9)

计量

文章访问数: 52
HTML全文浏览量: 63
PDF下载量: 20
被引次数: 0

1 馈源舱结构CFD模型
1.1 几何模型和风向角定义
1.2 计算方法和参数处理
1.3 网格模型
2 馈源舱结构气动力特性
2.1 凸起对馈源舱结构气动力特性影响
2.2 不同风向工况下馈源舱模型气动力特性
2.3 风速影响分析及斯托罗函数计算
3 馈源舱-索塔耦联体系振动特性
3.1 有限元模型及模态分析
3.2 支撑塔对模态结果的影响
4 耦联体系风振响应分析
4.1 风场模拟
4.2 风荷载计算
4.3 风振响应分析
5 结论

1 馈源舱结构CFD模型
1.1 几何模型和风向角定义
1.2 计算方法和参数处理
1.3 网格模型
2 馈源舱结构气动力特性
2.1 凸起对馈源舱结构气动力特性影响
2.2 不同风向工况下馈源舱模型气动力特性
2.3 风速影响分析及斯托罗函数计算
3 馈源舱-索塔耦联体系振动特性
3.1 有限元模型及模态分析
3.2 支撑塔对模态结果的影响
4 耦联体系风振响应分析
4.1 风场模拟
4.2 风荷载计算
4.3 风振响应分析
5 结论

参考文献(30)

施引文献

资源附件(0)

FAST馈源舱结构气动力特性及耦联系统风振响应研究

通讯作者: 付 兴(1988−)，男，辽宁人，副教授，博士，主要从事工程结构抗多灾及韧性评估研究(E-mail: fuxing@dlut.edu.cn)

计量

出版历程

RESEARCH ON THE AERODYNAMIC CHARACTERISTICS OF FAST FEED CABIN STRUCTURE AND THE WIND-INDUCED RESPONSES OF THE COUPLED SYSTEM

1 馈源舱结构CFD模型

1.1 几何模型和风向角定义

1.2 计算方法和参数处理

1.3 网格模型

2 馈源舱结构气动力特性

2.1 凸起对馈源舱结构气动力特性影响

2.2 不同风向工况下馈源舱模型气动力特性

2.3 风速影响分析及斯托罗函数计算

3 馈源舱-索塔耦联体系振动特性

3.1 有限元模型及模态分析

3.2 支撑塔对模态结果的影响

4 耦联体系风振响应分析

4.1 风场模拟

4.2 风荷载计算

4.3 风振响应分析

5 结论

计量

出版历程

目录

1 馈源舱结构CFD模型

1.1 几何模型和风向角定义

1.2 计算方法和参数处理

1.3 网格模型

2 馈源舱结构气动力特性

2.1 凸起对馈源舱结构气动力特性影响

2.2 不同风向工况下馈源舱模型气动力特性

2.3 风速影响分析及斯托罗函数计算

3 馈源舱-索塔耦联体系振动特性

3.1 有限元模型及模态分析

3.2 支撑塔对模态结果的影响

4 耦联体系风振响应分析

4.1 风场模拟

4.2 风荷载计算

4.3 风振响应分析

5 结论

通讯作者:
付　兴(1988−)，男，辽宁人，副教授，博士，主要从事工程结构抗多灾及韧性评估研究(E-mail: fuxing@dlut.edu.cn)