ANALYSIS ON THE INFLUENCE OF AXIAL FORCE ON SEISMIC SHEAR CAPACITY OF RC INTERIOR JOINTS
-
摘要:
对钢筋混凝土(RC)梁柱节点进行抗震受剪承载力计算是确保节点抗震性能的关键措施，我国《混凝土结构设计规范》(GB 50010−2010)的计算公式考虑轴力影响时目前暂时采用权宜性做法，其原因在于轴压力对节点受剪承载力的影响方式复杂、已有研究成果尚未充分澄清其影响规律。在OpenSees平台上，对梁柱节点单元(Beam-Column Joint Element, BCJE1)模型、考虑斜压杆双向应力扩散效应的BCJE2模型，以及将节点区离散为斜向混凝土压杆、水平及竖向钢筋弹簧的MBCJE模型的适用性进行了校核；选取合适的梁柱组合体原型试件，通过系列变化轴压力，采用模拟效果更优的MBCJE模型、BCJE2模型对RC节点及梁柱组合体进行参数分析。分析结果表明，节点剪压比ν高(ν⩾)时，节点损伤较严重，增大轴压力会降低组合体的延性，且轴压力较大或较小时轴力对节点峰值剪应力的有利影响均明显降低，GB 50010−2010的节点抗震受剪承载力计算式未充分考虑该特点，存在隐患；节点剪压比中等(0.2 \leqslant \nu < 0.3)时，按GB 50010−2010的计算方法考虑轴压力的有利影响基本可行，但轴压比较小时宜适当提高节点配箍；剪压比较低的节点(\nu < 0.2)可按GB 50010−2010的受剪承载力计算方法确定节点配箍。
Abstract:Calculating the seismic shear capacity of reinforced concrete (RC) beam-column joints is a key measure to ensure the seismic performance of the joints. The calculation formula in the Code for Design of Concrete Structures (GB 50010−2010) temporarily adopts an expedient method when considering the influence of axial force, which is related to the fact that the influence of axial force is complex and the existing research results have not clarified the effect of axial force. On the OpenSees platform, the applicability of the Beam Column Joint Element (BCJE1) model, the BCJE2 model considering the bidirectional stress dispersion effect of diagonal compression member, and the MBCJE model which discretizes the joint area into diagonal concrete compression members, horizontal and vertical steel bar springs, have been calibrated in this paper. The appropriate prototype of beam-column sub-assemblage specimens were selected, and the BCJE2 and MBCJE models with better simulation results were used to perform the parametric analysis of RC joints and beam-column sub-assemblage through a series of changes in axial load. The results show that when the shear-compression ratio of joint \nu is higher (\nu \geqslant 0.3), the joint damage is serious; increasing the axial load will reduce the ductility of the sub-assemblage, and the beneficial influence of the axial load on the peak shear stress of the joint will be significantly reduced when the axial compression load is large or small. The formula for calculating the seismic shear capacity of the joint in GB 50010−2010 does not fully consider this relationship, and there is a potential problem. When \nu is medium (0.2 \leqslant \nu < 0.3), it is generally feasible to consider the beneficial effect of axial force according to the calculation method of GB 50010−2010, but the stirrup of joint should be appropriately increased when the axial compression ratio is small. When \nu is low (\nu < 0.2), the stirrup of joints can be determined according to the calculation method for the shear capacity of joint in GB 50010−2010.
-
钢筋混凝土(reinforced concrete, RC)结构长期服役过程中容易受到多种环境因素的影响而发生性能劣化。在不拆除原有结构的前提下，对RC结构构件进行外部加固，不仅能够有效提升其服役性能，还能够节约维护成本[1]。外贴CFRP布是目前最为常用的RC结构构件加固方法之一[2 − 4]。
随着RC结构的高度和跨度不断增加，对大尺寸RC结构构件的设计理论提出了更高的要求。RC结构构件的剪切破坏具有强烈的脆性特征，其尺寸效应问题是亟待解决的科学难题之一[5 − 6]。以RC梁为例，YU等[7]开展了7根高为500 mm~1200 mm的无腹筋RC梁剪切破坏试验，CHANA[8]对36根梁高为150 mm~750 mm的RC简支梁进行了剪切破坏试验，结果均表明：无腹筋RC梁的抗剪强度存在明显的尺寸效应现象。GODAT等[9]对7根梁高为200 mm~600 mm的RC梁开展了剪切破坏试验，分析了U形CFRP布对RC梁抗剪性能的影响，发现：CFRP布的抗剪贡献在小尺寸试件中较大，并且CFRP布加固RC梁的抗剪强度亦存在明显的尺寸效应。LEUNG等[10]对15根梁高为180 mm~720 mm的RC梁进行了剪切破坏试验研究，分析了CFRP布U形包裹和全封闭包裹的加固方式对RC梁抗剪性能的影响，结果表明：CFRP布U形包裹RC梁的抗剪加固效果相对全包裹RC梁较差，且U形包裹RC梁的抗剪强度存在更明显的尺寸效应。
实际上，CFRP布的配纤率、粘贴方式、粘贴角度以及粘贴材料的性能[11 − 15]均会对加固梁的抗剪性能产生影响。以粘贴角度为例，SAADAH等[16]研究了CFRP布的粘贴角度(45°和90°)以及不同布置方式对RC梁抗剪性能的影响，结果表明：当CFRP布斜向布置以及减小CFRP布间距时，可以延缓RC梁裂缝的开展并增加其抗剪承载力。孙哲等[17]对CFRP布加固RC梁开展了剪切破坏试验，重点分析了CFRP布粘贴角度(45°、60°和90°)的影响，试验结果表明：不同粘贴角度对RC梁的加固效果具有明显区别，当CFRP布粘贴角度接近垂直于破坏斜裂缝时，其加固效果更好。DIVYA等[18]研究了单层CFRP布在不同粘贴角度(0°、45°和90°)及双层混合粘贴角度对RC梁抗剪性能的影响，结果表明：单层粘贴时，CFRP布45°粘贴具有更好的加固效果；双层粘贴时，CFRP布45°+90°粘贴具有更好的加固效果。
基于上述分析可见，已有研究均表明CFRP布粘贴角度能够影响加固梁的抗剪性能，但其对加固RC梁的抗剪性能的影响机理以及对尺寸效应行为的定量影响规律仍有待深入探讨。鉴于此，为深入探究CFRP布粘贴角度对RC梁尺寸效应的影响，本文基于前期开展的CFRP布45°和90°粘贴加固RC梁抗剪性能及尺寸效应试验，采用数值试验法进一步分析CFRP布粘贴角度为0°、30°和60°时不同尺寸RC梁的剪切破坏行为，研究CFRP布粘贴角度对加固梁抗剪性能和尺寸效应的影响规律，并最终提出考虑粘贴角度影响的CFRP布加固无腹筋RC梁的名义抗剪强度尺寸效应律。
1 试验与数值模拟方案设计
1.1 试验概况
文献[11,19 − 20]对相同粘贴角度下的CFRP布加固(亦包含未加固的)无腹筋RC梁剪切破坏行为进行了研究，主要分析剪跨比和配纤率对加固梁抗剪性能及尺寸效应的影响。本文选取其中相同剪跨比(λ=1.5)和相同配纤率( \rho _{\text{f}} = 0.0835\text{%} )的试件，研究CFRP布不同粘贴角度对RC梁的抗剪性能及尺寸效应的影响。为避免RC梁发生弯曲破坏，试验梁的纵筋率ρ设置为2.5%。试验梁的尺寸、配筋详情以及CFRP布的布置情况如图1所示。表1给出了试件详细的几何参数，试件命名以“S-45°”为例，“S”表示截面尺寸为100 mm×300 mm的试件，“45°”表示CFRP布的粘贴角度(CFRP布与RC梁长轴间的夹角)为45°。CFRP布采用U形包裹的加固方式，所有加固梁的配纤率ρf均相同，其定义为[21 − 23]：
\rho _{\text{f}} = \frac{{2n w_{\text{f}} t_{\text{f}}}}{{b s_{\text{f}}}} = 0.0835\text{%} (1) 式中：n为CFRP布的加固层数；wf为CFRP布的宽度；tf为单层CFRP布的厚度；b为RC梁的截面宽度；sf为相邻两CFRP布的中心线间的距离。
![]()
图 1 试验梁详情以及CFRP布的布置情况Figure 1. Details of the test beam and the layout of the CFRP sheets表 1 试验中试件的几何参数Table 1. Geometrical dimensions of specimens in the test试件名称 θ/(°) h/mm h0/mm n tf/mm wf/mm sf/mm 未加固S − 300 245 − − − − S-45° 45 300 245 1 0.167 50 200 S-90° 90 300 245 1 0.167 50 200 未加固M − 600 507 − − − − M-45° 45 600 507 2 0.167 100 400 M-90° 90 600 507 2 0.167 100 400 未加固L − 900 784 − − − − L-45° 45 900 784 3 0.167 150 600 L-90° 90 900 784 3 0.167 150 600 注：θ为CFRP布的粘贴角度；h为试件的截面高度；h0为试件的有效截面高度；n为CFRP布的粘贴层数；tf为单层CFRP布的厚度；wf为CFRP布的宽度；sf为相邻两CFRP布的间距。 为减小离散性，试验梁保证同批次浇筑。按照《混凝土物理力学性能试验方法标准》(GB/ T 50081−2019)[24]测定混凝土的抗压和抗拉强度，在标准养护28 d后，测定混凝土的平均立方体抗压强度fcu为49.2 MPa，平均圆柱体抗压强度f_{\mathrm{c}}' 为44.3 MPa，平均劈拉强度ft为2.77 MPa。
试验采用以聚丙烯腈基12K小丝束碳纤维为原料的CFS一级300克CFRP布，单层厚度为0.167 mm的 CFRP的重量为300 g/m2。按照《定向纤维增强复合材料拉伸性能试验方法》(GB/T 3354−2014)[25]测定CFRP布的性能指标，经拉伸试验测量得出：CFRP布的抗拉强度σt为3820 MPa，弹性模量E为232 GPa，极限应变ε为0.016。
粘结胶采用配套的环氧树脂胶，按照《树脂浇铸体性能试验方法》(GB/T 2567−2021)[26]测定其力学性能指标，经拉伸测试得出：粘结胶的伸长率s为1.8%，抗拉强度σt为42 MPa，弹性模量E为2.512 GPa。
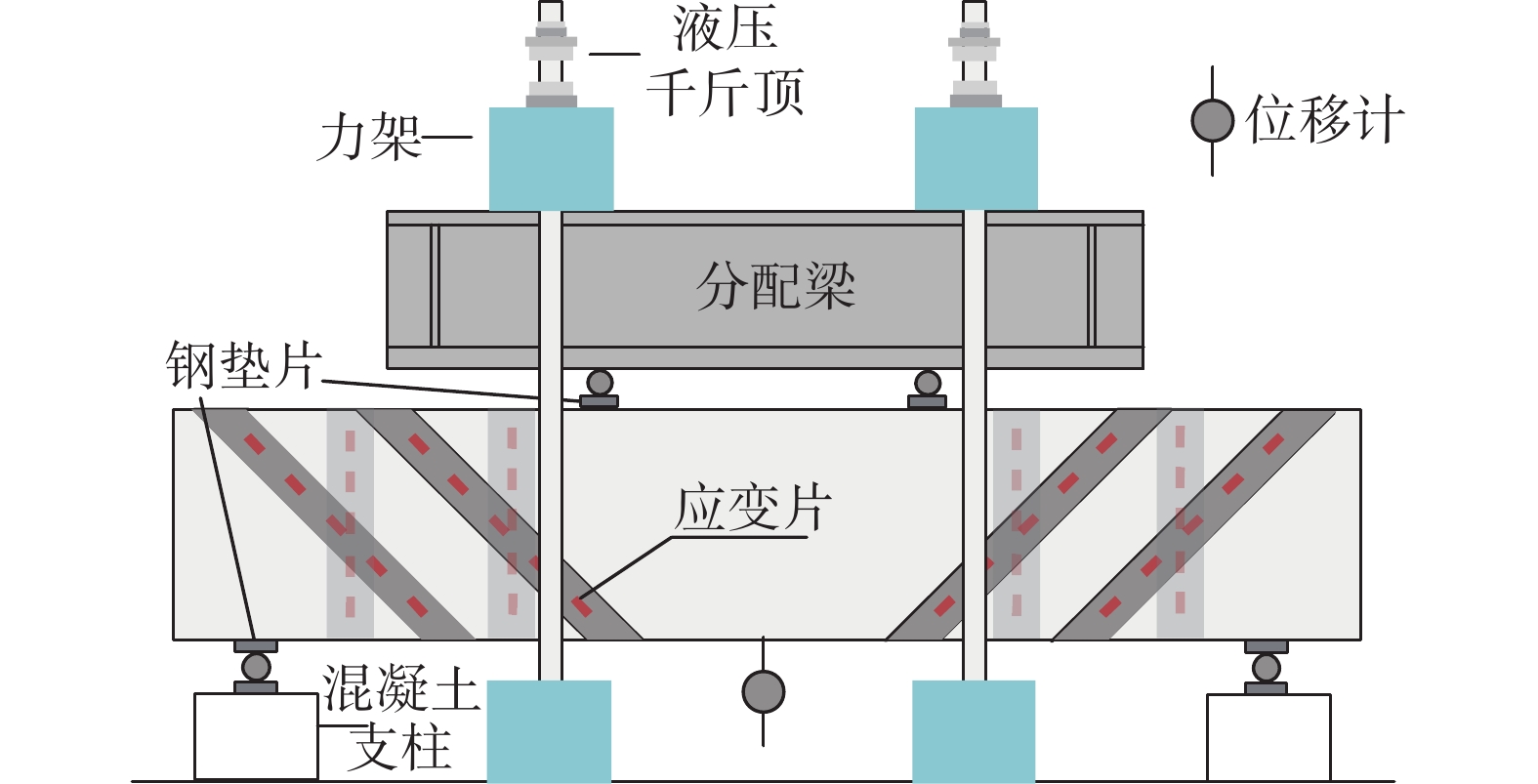
试验中量测和记录的主要内容为：加载过程中的荷载变化值、CFRP布上的应变值、梁的竖向位移、裂缝宽度及其发展延伸情况。试件在400T力架上进行加载试验，为了避免加载过程中在加载点和支座处发生局部受压破坏，在力传感器下方和支座处放置了具有一定刚度的钢垫片。试验采用静力加载的方案，加载速度为1 kN/s，加载方式为两点对称加载。试验加载装置如图2所示。
试验结果表明：当CFRP布的粘贴角度为45°斜贴时，加固梁具有更高的抗剪承载力和刚度。
1.2 数值分析
受经济条件的限制，试验仅研究了45°和90°两种CFRP布粘贴角度对加固梁抗剪性能的影响。为深入探究CFRP布粘贴角度对加固梁抗剪性能及其尺寸效应的影响，本文在原试验的基础上，采用ABAQUS有限元分析软件，拓展分析0°、30°和60°的CFRP布粘贴角度工况。需要强调的是，除CFRP布粘贴角度外，其它参数与试验均保持完全一致。
1.2.1 CFRP布加固RC梁细观模型建立
细观数值模型能较好地反应混凝土的非均质特性。根据文献[27]，将混凝土看作是由骨料、砂浆和界面过渡区(ITZ)组成的三相材料。图3给出了CFRP布加固RC梁的三维细观模型。
![]()
图 3 CFRP布加固RC梁三维细观模型Figure 3. Three-dimensional meso-model of RC beam strengthened by CFRP sheets骨料强度较高，在混凝土断裂中假定其不发生破坏，故将其设为理想弹性体[28]。由于混凝土材料在外荷载作用下会产生不可恢复的塑性变形，由LUBLINER等[29]提出，且经LEE和FENVES[30]改进的塑性损伤模型可以很好地反映这种变形，砂浆在材料组分的架构上与混凝土相似，并且一般将ITZ视为弱化的砂浆，故砂浆和ITZ的力学特性采用塑性损伤模型来描述[31]。钢筋为均质材料，其力学行为采用理性弹塑性本构模型来描述，钢筋和混凝土之间的粘结滑移行为通过设置非线性弹簧单元来描述[32 − 33]。CFRP布在脆性断裂前看作线弹性材料[34 − 35]，发生脆性破坏后采用Hashin准则[36]来表征CFRP布的力学行为。考虑到CFRP布的剥离，CFRP布和混凝土之间的粘结滑移行为采用简化的双线性模型来描述[37]。三维细观模型的详细建模过程见文献[38]。
以CFRP布粘贴角度为45°的加固梁来说明本文采用细观模型的合理性和准确性。表2给出了混凝土细观组分以及钢筋的力学参数，CFRP布的力学参数取自试验的测量值。ITZ的力学参数通过对砂浆力学参数进行一定的折减得到[39]，进而通过反复模拟试算，选取最接近试验值的一组数据作为其力学参数。按表2模拟得出的混凝土单轴抗压强度为48.3 MPa，与试验值49.2 MPa较为接近，即认为所选参数是合理的。
表 2 混凝土细观组分及钢筋力学参数Table 2. Meso-components of concrete and mechanical parameters of reinforcements力学参数 砂浆 骨料 ITZ 纵筋(C14) 纵筋(C40) 弹性模量E/GPa *51.4 #70.0 ^46.3 *205 *210 泊松比ν *0.2 *0.2 ^0.2 *0.3 *0.3 断裂能Gc /(J/m2) 50 30 抗压强度σc /MPa *49.2 − ^42.1 − − 抗拉强度σt /MPa *2.77 − ^2.2 − − 屈服强度fy /MPa − − − *382 *486 注：*为试验所测值；^为模拟中开展边长为150 mm的混凝土标准立方体试块单轴压缩试验的反复验算值，断裂能从[40]中引用。 如图4所示，将模拟结果与试验结果进行对比，可以看到模拟得到的破坏模式、剪力-跨中位移曲线和CFRP布应变分布情况与试验结果均吻合较好，验证了模型的合理性和准确性。
1.2.2 构件设计
本文采用1.2.1节已验证的三维细观数值模拟方法，在试验工况的基础上扩建了粘贴角度为0°、30°和60°的CFRP布加固RC梁模型。试件的剪跨比λ为1.5，纵筋率ρ为2.5%，配纤率ρf为0.0835%，与试验保持一致。试件命名以“S’-0°”为例，表示截面尺寸为100 mm×300 mm、CFRP布粘贴角度为0°的加固梁，表3给出了模拟的试件几何参数。
表 3 模拟中构件几何参数Table 3. Geometrical dimensions of members in numerical analysis构件名称 θ/(°) h/mm h0/mm n tf/mm wf/mm sf/mm S’-0° 0 300 245 1 0.167 50 200 S’-30° 30 300 245 1 0.167 50 200 S’-45° 45 300 245 1 0.167 50 200 S’-60° 60 300 245 1 0.167 50 200 S’-90° 90 300 245 1 0.167 50 200 M’-0° 0 600 507 2 0.167 100 400 M’-30° 30 600 507 2 0.167 100 400 M’-45° 45 600 507 2 0.167 100 400 M’-60° 60 600 507 2 0.167 100 400 M’-90° 90 600 507 2 0.167 100 400 L’-0° 0 900 784 3 0.167 150 600 L’-30° 30 900 784 3 0.167 150 600 L’-45° 45 900 784 3 0.167 150 600 L’-60° 60 900 784 3 0.167 150 600 L’-90° 90 900 784 3 0.167 150 600 2 结果与分析
CFRP布加固RC梁的尺寸效应现象主要来自三个方面的原因：1) 混凝土材料本身的非均质特性；2) 钢筋和混凝土材料之间的相互作用；3) CFRP布与混凝土之间的非线性相互作用[41]。目前RC梁尺寸效应在CFRP布不同粘贴方式加固方面的研究还较少。对于不同粘贴角度下CFRP布加固RC梁的尺寸效应行为，仍需开展进一步的研究工作。
CFRP布不同的粘贴角度会对RC梁产生不同的加固效果，进而会对加固梁的抗剪性能产生影响。随着CFRP布粘贴角度的改变，加固梁的脆性也可能发生变化，进而对加固梁的尺寸效应行为产生影响。
2.1 破坏模式
图5给出了CFRP布U型加固RC梁在不同构件尺寸(梁高为300 mm、600 mm和900 mm)、不同粘贴角度(0°、30°、45°、60°和90°)下的破坏模式图。从图中可以看出，所有试件均发生了明显的剪切破坏，最终破坏时的主斜裂缝为自加载点至支座端的一条贯通斜裂缝，值得注意的是，CFRP布的粘贴角度对加固梁主斜裂缝的倾角影响极小，主斜裂缝的倾角主要受加载点和支座相对位置的影响，其值约为40°。
2.2 剪力-跨中位移曲线
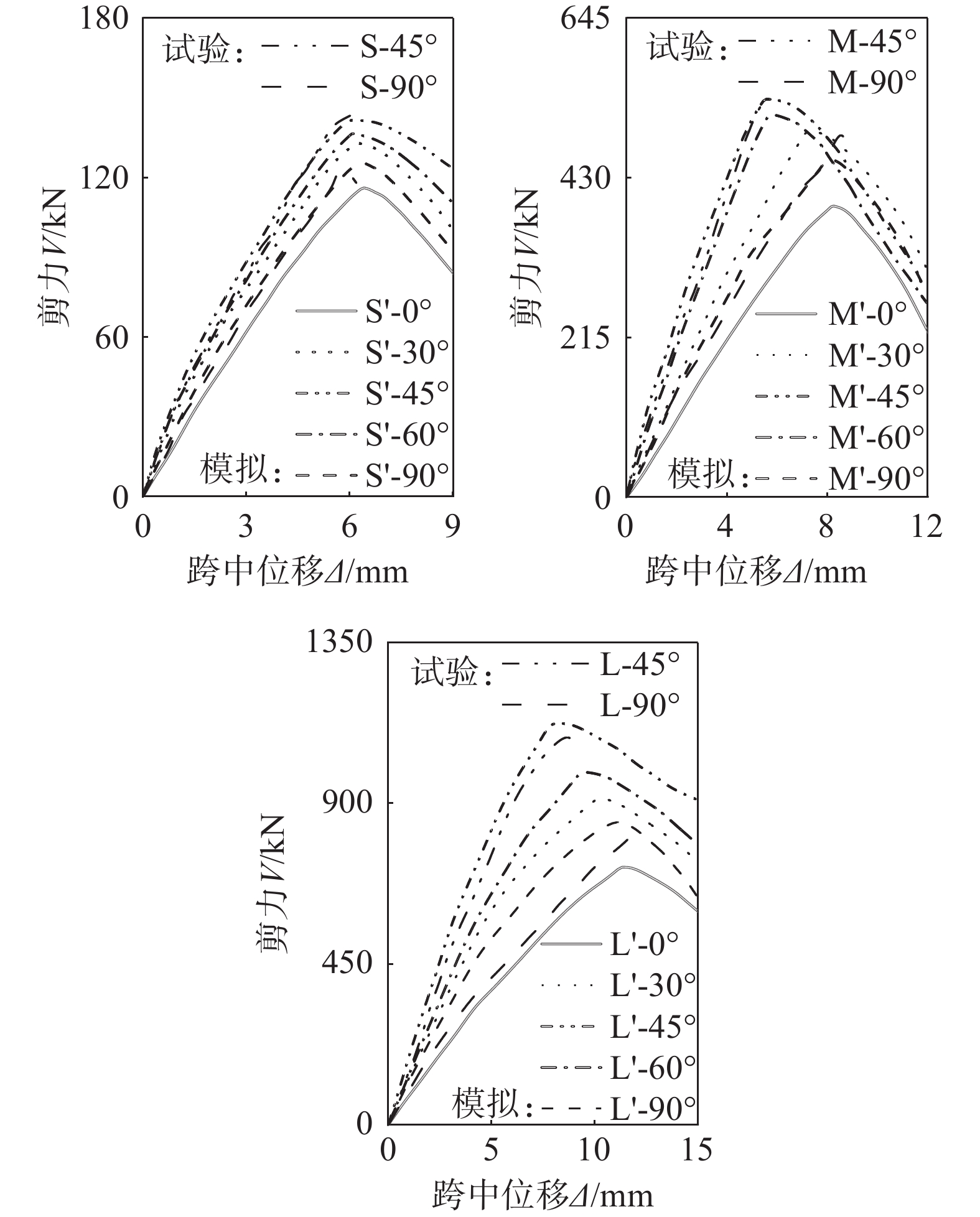
在CFRP布的不同粘贴角度下，加固梁的剪力V随跨中位移Δ的变化如图6所示。从图6中可以看出，各试件在加载前期具有较高的刚度，随着荷载的增加，其刚度不断退化，这与文献[42]的结论一致。在45°粘贴角度下，加固梁具有最高的破坏荷载和刚度，粘贴角度为60°、30°、90°和0°的加固梁的破坏荷载和刚度依次次之。加固梁破坏时主斜裂缝的倾角主要受加载点和支座点相对位置的影响。本文各试件的剪跨比均为1.5，主斜裂缝的倾角均约为40°。由此可知，越接近于垂直主斜裂缝的CFRP布粘贴角度，CFRP布对RC梁的加固效果越好，这与NORRIS等[43]的结论一致。
表4给出了试验量测得到的加固梁的主要性能指标以及模拟中提取到的结果。由表4可知：在试验中，相同截面尺寸下，CFRP布粘贴角度为45°的加固梁比粘贴角度为90°的加固梁具有更高的P0、V0和Vu。以梁高为300mm的加固梁为例，CFRP布45°粘贴相比90°粘贴，其P0、V0和Vu分别增加了33%、83%和17%。这表明45°粘贴相比于90°粘贴，不仅提高了加固梁的整体抗剪承载力，而且能够更好地限制裂缝的开展。在相同粘贴角度下，随着截面尺寸的增加，试件的P0、V0和Vu均存在一定程度的提高。以90°粘贴的加固梁为例，当梁高由300 mm增至600 mm时，其P0、V0和Vu分别提高了25%、301%和293%。在模拟中可以看出，CFRP布不同粘贴角度下对RC梁的抗剪承载力提升范围为8%~83%，且CFRP布的粘贴角度为45°、60°、30°、90°和0°时，对应加固梁的抗剪承载力提升效果依次递减，以梁高为600 mm的加固梁为例，CFRP布的粘贴角度为45°、60°、30°、90°和0°时，对RC梁的抗剪承载力分别提升了57%、51%、45%、33%和15%。这是由于CFRP布的抗剪贡献一方面来自CFRP布受拉直接参与的抗剪贡献，另一方面来自CFRP布对混凝土的约束作用对RC梁抗剪承载力的提高[41]，当CFRP布的粘贴角度越接近垂直于主斜裂缝时，其对裂缝的开裂限制效果越好，从而能更好地提高加固梁的抗剪性能。
表 4 试验和模拟主要结果Table 4. Main results of tests and simulations试件名称 P0/kN V0/kN Pu/kN Vu/kN Δ/mm 试验 未加固S 18 41 215.2 107.6 5.2 S-45° 64 139 290.0 145.0 6.2 S-90° 48 76 248.5 124.3 5.8 模拟 S’-0° − − 233.2 116.6 6.4 S’-30° − − 265.6 132.8 6.2 S’-45° − − 283.0 141.5 6.0 S’-60° − − 275.4 137.7 6.1 S’-90° − − 251.6 125.8 6.3 试验 未加固M 53 297 683.5 341.8 6.19 M-45° 141 312 1049.8 524.9 5.4 M-90° 60 305 977.8 488.9 8.5 模拟 M’-0° − − 786.2 393.1 8.2 M’-30° − − 989.0 494.5 7.2 M’-45° − − 1071.6 535.8 5.5 M’-60° − − 1033.6 516.8 5.8 M’-90° − − 911.8 455.9 8.0 试验 未加固L 68 432 1081.8 580.7 8.64 L-45° 189 768 2167.6 1083.8 8.7 L-90° 82 684 1628.3 816.4 11.9 模拟 L’-0° − − 1462.0 731.0 11.3 L’-30° − − 1838.2 919.1 10.1 L’-45° − − 2249.6 1060.2 7.8 L’-60° − − 1979.4 989.7 9.3 L’-90° − − 1693.6 846.8 11.0 注：P0为弯曲开裂荷载；V0为初始斜裂缝荷载；Pu为极限荷载；Vu为最大剪力；Δ为极限荷载所对应的跨中位移。 2.3 CFRP布应变
沿梁高不同位置的CFRP布应变分布情况体现了加固梁中CFRP布发挥加固效果的情况。图7给出了不同粘贴角度下CFRP布的最大应变沿梁高变化情况(由于0°粘贴的CFRP布均在同一高度，因此未给出)。从图7中可以看出，近加载端CFRP布的应变分布情况为：靠近梁上端的应变值较大，而靠近梁下部的应变值较小；近支座端的CFRP布应变分布则恰好相反。这主要反映了不同粘贴角度的加固梁破坏后，混凝土的裂缝延伸情况基本相同。CFRP布的应变分布反映试件裂缝的开裂情况，在试件最终破坏前，其剪跨段的斜裂缝出现情况有随机性，同样地，CFRP布的应变分布在局部亦有一定差异。对比不同截面尺寸加固梁上CFRP布的应变情况，可以看到：随着加固梁截面尺寸的增大，CFRP布的最大应变值逐渐减小。这是由于在保持配纤率一致的前提下，RC梁截面尺寸越大，对应的CFRP布的厚度和宽度越大(即CFRP布的横截面面积越大)，当CFRP布产生相同的抗剪贡献值时，其所需产生的应变值较小，这与HOSEN等[44]的结论一致。值得注意的是，CFRP布最大应变均未达到其极限拉应变，因此CFRP布均未发生断裂。
![]()
图 7 CFRP布的最大应变沿梁高变化Figure 7. Distribution of the maximum strain on CFRP sheets along the beam depth2.4 CFRP布抗剪贡献
目前，计算CFRP布加固RC梁总抗剪承载力多采用叠加法[22 − 23]，即加固梁的总抗剪承载力Vu分为混凝土的抗剪贡献Vc和CFRP布的抗剪贡献Vf两部分：
V_{\text{u}} = V_{\text{c}} + V_{\text{f}} (2) 本文以未加固RC梁作为对照组，其抗剪承载力为Vc，则CFRP布的抗剪贡献Vf可由总抗剪承载力Vu减混凝土的抗剪贡献Vc得到：
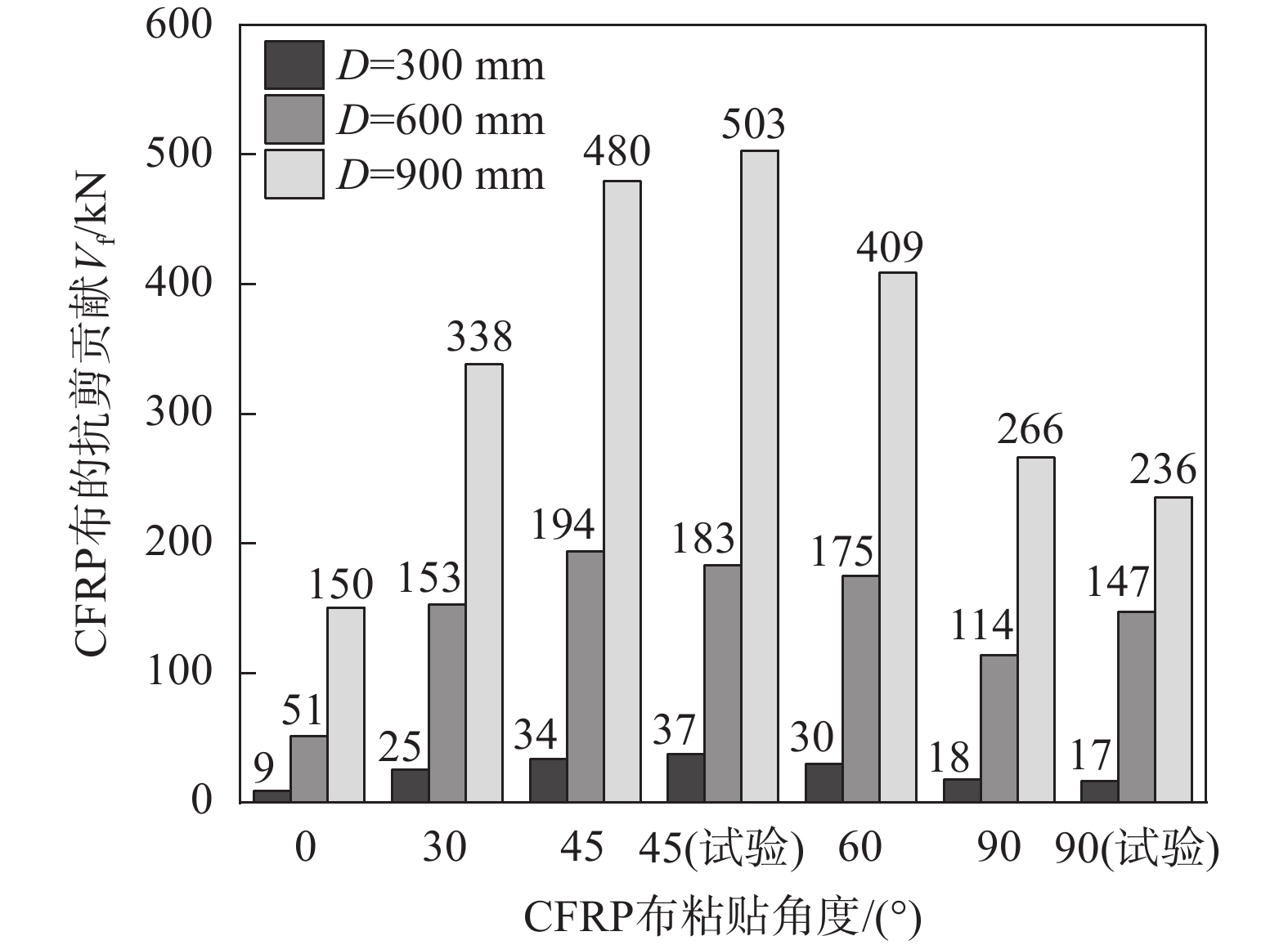
V_{\text{f}} = V_{\text{u}} - V_{\text{c}} (3) 图8给出了不同粘贴角度下CFRP布的抗剪贡献对比情况，以梁高为600 mm的加固梁为例，粘贴角度为0°、30°、45°、60°和90°的加固梁的CFRP布的抗剪贡献占比分别为15%、45%、57% (试验54%)、51%和33%(试验43%)，从图8中也可以直观看出，倾斜45°粘贴时CFRP布的抗剪贡献值最大，其对RC梁的加固效果更好；水平0°粘贴时的加固效果较差。
3 名义抗剪强度分析及尺寸效应律
3.1 名义抗剪强度分析
名义抗剪强度，是指材料或构件有效单位截面面积上承担的剪力，可由式(4)计算得到[45 − 46]：
\tau _{\text{u}} = \frac{{V_{\text{u}}}}{{bh_{\text{0}}}} (4) 式中：Vu为试件的抗剪承载力；b和h0分别为试件的截面宽度和截面有效高度。
尺寸效应，是指以名义强度为代表的材料或构件力学性能指标随结构尺寸的增大呈减小趋势[47]。图9给出了加固梁在不同CFRP布粘贴角度下，其名义抗剪强度随截面高度的变化趋势。从图中可以看出，对于CFRP布粘贴角度相同的试件，其名义抗剪强度随截面尺寸的增大而逐渐减小，表现出了明显的尺寸效应现象。对于相同截面尺寸的试件，在不同的粘贴角度下，CFRP布对加固梁的名义抗剪强度有不同程度的提高。45°粘贴角度对加固梁有较好的加固效果，60°、30°、90°和0°粘贴角度对加固梁的加固效果依次减弱。同时，不同的粘贴角度下，随截面尺寸的增加，加固梁的名义抗剪强度有不同程度的下降。从图中可以看出，未加固梁的名义抗剪强度下降最显著，具有最明显的尺寸效应行为，0°、90°、30°、60°和45°粘贴角度下加固梁的尺寸效应依次减弱。当粘贴角度为0°、90°、30°、60°和45°时，加固梁的梁高从300 mm增至900 mm，其名义抗剪强度下降分别约为35%、31%、27%、25%和23%，未加固梁下降为44%。这是由于CFRP布加固RC梁在提高其名义抗剪强度的同时，通过限制裂缝的开裂提高加固梁的整体性和稳定性，因此其尺寸效应得到了削弱。且当CFRP布的粘贴角度越接近垂直于主斜裂缝时，其对裂缝的开裂限制效果越好，尺寸效应被削弱程度越高，故未加固RC梁具有最明显的尺寸效应现象。
3.2 尺寸效应律
3.2.1 抗剪强度尺寸效应理论公式
针对无腹筋RC梁的尺寸效应，文献[48]提出了基于断裂力学理论的混凝土抗剪强度尺寸效应公式：
\tau _{\text{u}} = \frac{{v_{\text{0}}}}{{\sqrt {1 + D/d_{\text{0}}} }} (5) 式中：v0和d0为反应混凝土类型的经验系数；D表征构件的特征截面尺寸(本文中取加固梁的截面高度)。
由3.1节的分析可知，加固梁的名义抗剪强度随CFRP布粘贴角度的不同而有不同程度的提高，这里采用系数φ(θ)来表征CFRP布粘贴角度对加固梁名义抗剪强度的影响。此外，CFRP布在承受剪力的同时还会抑制斜裂缝的扩展，这种约束效应能够削弱RC梁名义抗剪强度随构件尺寸增大的下降趋势[49]，这种削弱效果采用系数β来表征。
结合式(5)，本文提出了考虑CFRP布粘贴角度对加固梁抗剪强度影响的强度提高系数φ(θ)和由于CFRP布的加固而对尺寸效应产生影响的尺寸效应削弱系数β的抗剪强度尺寸效应公式为：
\tau _{\text{u}} = \frac{{v_{\text{0}}}}{{\sqrt {1 + D/d_{\text{0}}} }}\varphi (\theta ) \beta (6) 3.2.2 强度提高系数φ(θ)的确定
加固梁的名义抗剪强度随CFRP布粘贴角度的不同而有不同程度的提高，当粘贴角度接近垂直于主斜裂缝时，其加固效果较好。以未加固梁为参照组，表5中给出了不同粘贴角度下加固梁的名义抗剪强度与对照组的比值。
表 5 强度提高系数φ(θ)的值Table 5. The value of strength increase coefficient φ(θ)试件名称 φ(θ) 试件名称 φ(θ) 试件名称 φ(θ) S-0° 1.08 M-0° 1.15 L-0° 1.26 S-30° 1.23 M-30° 1.45 L-30° 1.58 S-45° 1.32 M-45° 1.57 L-45° 1.83 S-45°
(试验)1.35 M-45°
(试验)1.54 L-45°
(试验)1.87 S-60° 1.28 M-60° 1.51 L-60° 1.70 S-90° 1.17 M-90° 1.33 L-90° 1.46 S-90°
(试验)1.16 M-90°
(试验)1.43 L-90°
(试验)1.41 这里采用二次幂函数来表示强度提高系数φ(θ)和CFRP布粘贴角度θ之间的关系，其表达式为：
\varphi {\text{(}}\theta {\text{)}} = A - B{{\text{(}}\theta - C{\text{)}}^2} (7) 式中：系数A、系数B和系数C经拟合确定；θ为CFRP布的粘贴角度，图10给出了强度提高系数φ(θ)随CFRP布粘贴角度θ的变化趋势，并给出了不同截面尺寸下φ(θ)的表达式。最后结合系数A和B与截面尺寸的关系拟合出统一的表达式为：
\varphi {\text{(}}\theta {\text{)}} = {\text{(}}1.1 + 0.8 \times D{\text{)}} - {\text{(}}0.3{\text{ + 1}}{\text{.8}} \times D{\text{)}} \times {10^{ - 4}} \times {{\text{(}}\theta - 51{\text{)}}^2}{\kern 1pt} {\kern 1pt} (8) ![]()
图 10 强度提高系数φ(θ)的确定Figure 10. Determination of the improvement coefficient φ(θ) of strength3.2.3 尺寸效应削弱系数β的确定
CFRP布对RC梁有明显的加固效果，同时也削弱了RC梁的尺寸效应。并且随着配纤率的增加，RC梁尺寸效应的削弱程度越来越明显。这里用双曲正切函数来表示随着配纤率ρf的增加尺寸效应削弱系数β的变化情况：
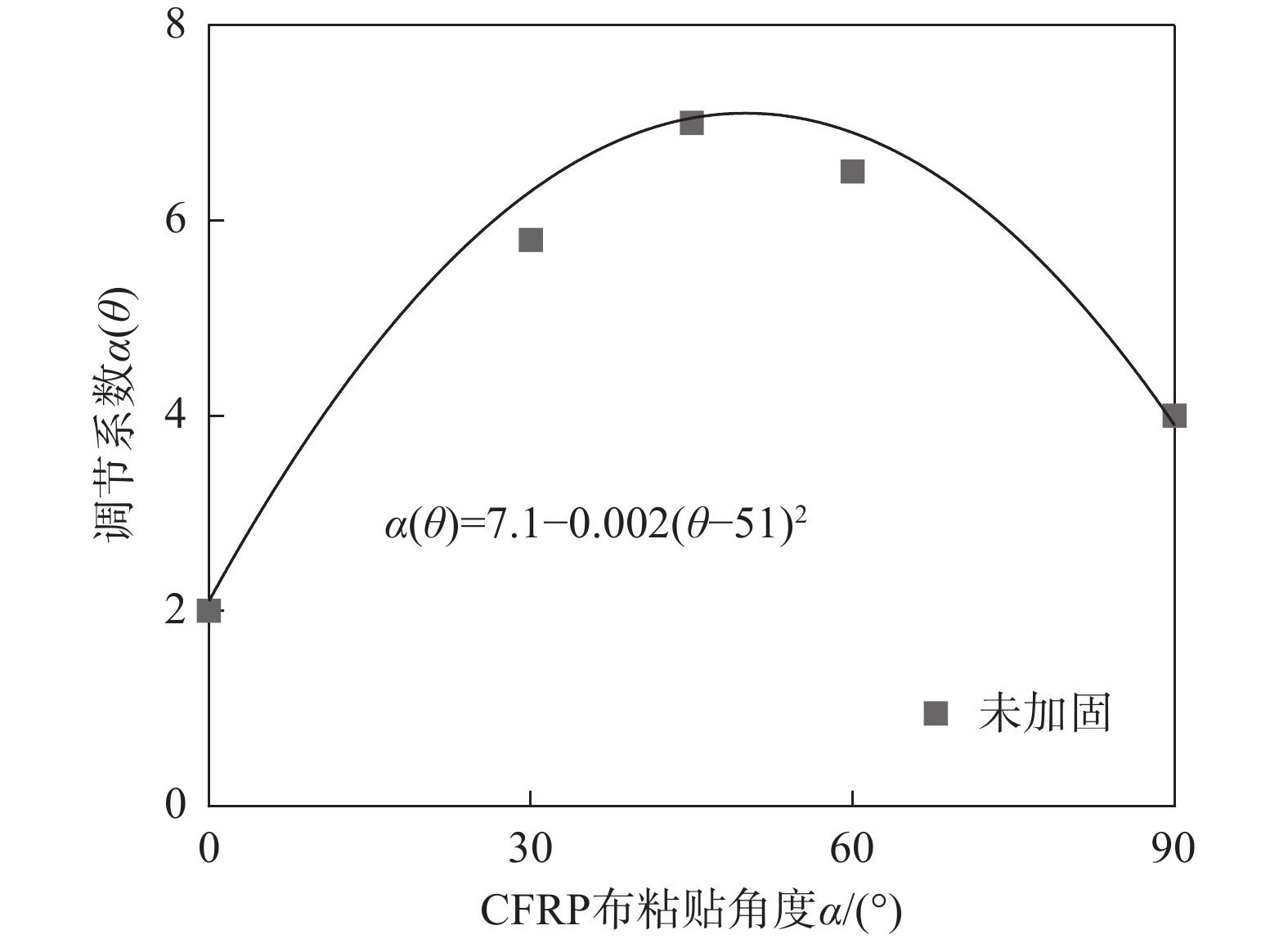
\beta=\left\{\begin{aligned} & 1, & & \rho_{\text{f}}=0 \\ & \left(\frac{1.2f_{\mathrm{t}}^{0.89}\sqrt{1+D/d_0}}{v_0}-1\right)\text{tanh}(\alpha(\theta)\rho_{\text{f}})+1, & & \rho_{\text{f}} > 0\end{aligned}\right. (9) 式中：ft为混凝土的抗压强度；v0和d0为反映混凝土类型的经验系数；α(θ)为反映尺寸效应削弱速率的调节系数。对未加固对照组梁的名义抗剪强度进行回归分析可得：v0为13.6，d0为27.0。α(θ)的值为将理论结果与试验及模拟结果进行拟合对比得出，表6给出了调节系数α(θ)随CFRP布粘贴角度变化的取值，根据这些值拟合出了调节系数α(θ)的表达式如图11所示。
表 6 α(θ)的取值Table 6. The value of α(θ)θ/(°) 0 30 45 60 90 α(θ) 2.0 5.8 7.0 6.5 4.0 图12给出了由上述所提公式得出的理论计算值与模拟(试验)值的对比，并增加了CFRP布粘贴角度为51°时加固梁的模拟结果。从图中可以看出，理论计算值与模拟(试验)值吻合较好，说明本文所提的尺寸效应公式具有较好的准确性。
![]()
图 12 名义抗剪强度理论值与试验结果对比Figure 12. Comparisons of the nominal shear strength between the theoretical values and test results3.3 验证
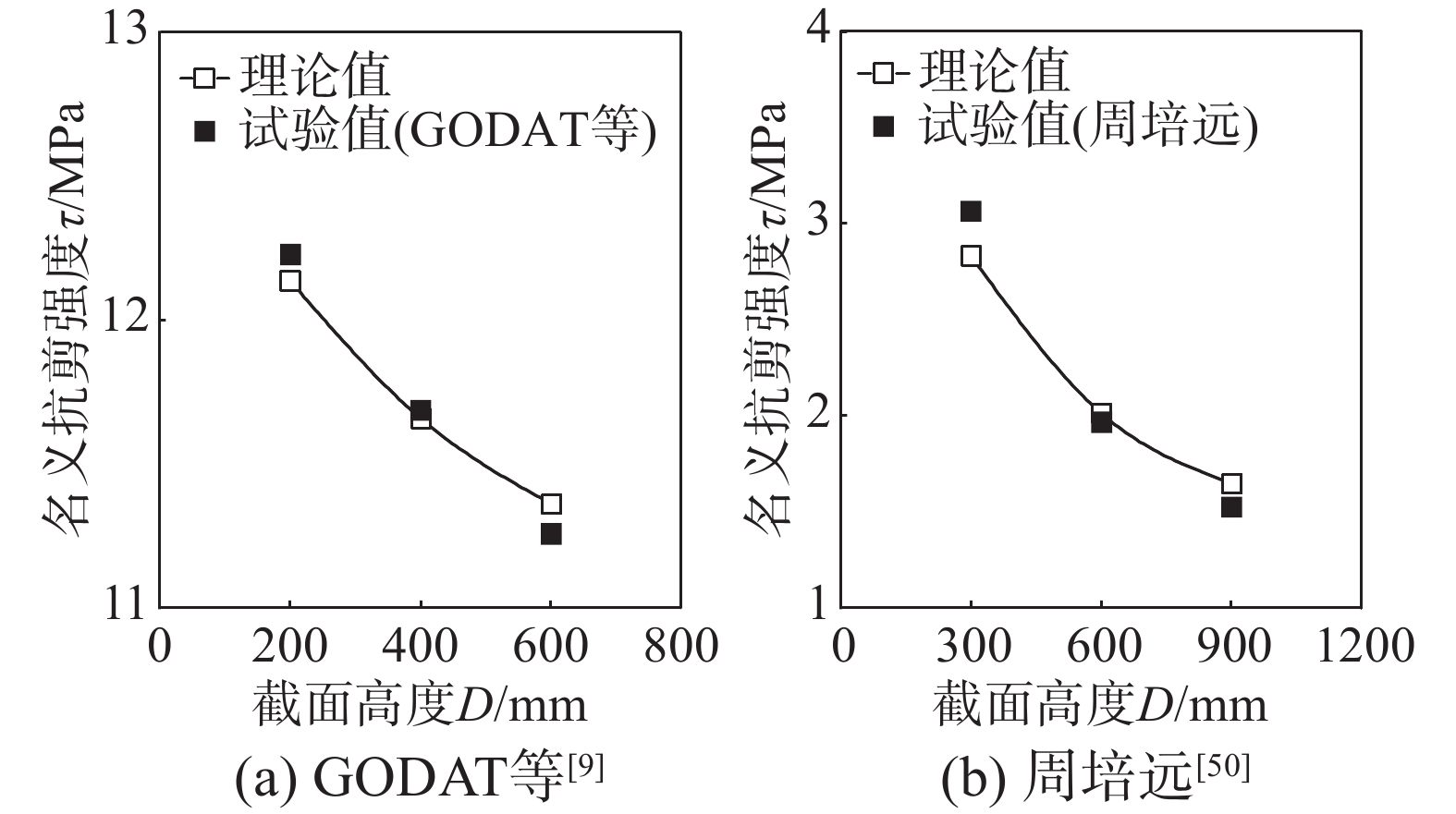
图13给出了由上述所提公式计算所得的理论值与现有的尺寸效应相关试验值[9, 50]的对比，从图中可以看出理论值与试验值亦吻合较好，验证了考虑CFRP布粘贴角度的扩展尺寸效应律的合理性。
![]()
4 结论
本文以6根梁高分别为300 mm、600 mm和900 mm的CFRP布45°/90°加固无腹筋RC梁的剪切破坏试验结果为基础，在模拟中扩展了CFRP布粘贴角度为0°、30°和60°的加固梁的剪切性能研究。重点分析了CFRP布粘贴角度对加固梁名义抗剪强度及尺寸效应的影响机制与规律。主要结论如下：
(1) CFRP布不同粘贴角度下的加固梁，最终的破坏模式基本相同，但加固梁的抗剪承载力和刚度受到较为明显的影响。当CFRP布粘贴角度接近垂直于主斜裂缝时，梁抗剪承载力和刚度较大。
(2) 不同粘贴角度的CFRP布加固梁均表现出明显的尺寸效应，且粘贴角度对加固梁的名义抗剪强度存在较大影响。粘贴角度对加固梁的抗剪强度尺寸效应趋势亦有明显的影响，当CFRP布粘贴角度接近垂直于主斜裂缝时，加固梁的尺寸效应下降趋势受到明显的削弱，即CFRP布发挥的加固效果显著。
(3) 在混凝土材料层次尺寸效应律基础上扩展建立的构件层次尺寸效应律，较好地反应粘贴角度对CFRP布斜贴加固RC梁的名义抗剪强度尺寸效应的影响规律。
值得注意的是，虽然CFRP布在不同粘贴角度下对RC梁的加固效果有所不同，但是其最大加固效果是有限的，本文建议CFRP布对RC梁的抗剪承载力的提升范围取值在1.0~2.0以内。
-
![]()
![]()
图 4 中间层中节点梁柱组合体的有限元模型
Figure 4. Finite element model of beam-column sub-assemblage with interior joint
![]()
图 5 试件J-16试验结果与有限元计算结果对比
Figure 5. Comparison between simulation results and test results of specimen J-16
![]()
图 6 试件CL-4基于MBCJE模型的计算结果
Figure 6. Calculation results of specimen CL-4 based on MBCJE model
![]()
图 7 试件CL-4基于BCJE2模型的计算结果
Figure 7. Calculation results of specimen CL-4 based on BCJE2 model
![]()
图 8 {n_{\text{t}}}-{\tau _{{\text{max}}}}和{n_{\text{t}}}-{\gamma _{{\text{max}}}}关系(\nu \geqslant 0.3)
Figure 8. Relationships of {n_{\text{t}}}-{\tau _{{\text{max}}}}and {n_{\text{t}}}-{\gamma _{{\text{max}}}}(\nu \geqslant 0.3)
![]()
图 9 {n_{\text{t}}}-{\mu _\Delta }和{n_{\text{t}}}-\mu _{\text{ε}}关系(\nu \geqslant 0.3)
Figure 9. Relationships of {n_{\text{t}}}-{\mu _\Delta } and {n_{\text{t}}}-\mu _{\text{ε}}(\nu \geqslant 0.3)
![]()
图 10 {n_{\text{t}}}-{\tau _{{\text{max}}}}和{n_{\text{t}}}-{\gamma _{{\text{max}}}}关系(0.2 < \nu < 0.3)
Figure 10. Relationships of {n_{\text{t}}}-{\tau _{{\text{max}}}}and {n_{\text{t}}}-{\gamma _{{\text{max}}}}(0.2 < \nu < 0.3)
![]()
图 11 {n_{\text{t}}}-{\mu _\Delta }和{n_{\text{t}}}-\mu _{\text{ε}}关系(0.2 < \nu < 0.3)
Figure 11. Relationship s of {n_{\text{t}}}-{\mu _\Delta } and {n_{\text{t}}}-\mu _{\text{ε}}(0.2 < \nu < 0.3)
![]()
图 12 {n_{\text{t}}}-{\tau _{{\text{max}}}}和{n_{\text{t}}}-{\gamma _{{\text{max}}}}关系(\nu \leqslant 0.2)
Figure 12. Relationship s of {n_{\text{t}}}-{\tau _{{\text{max}}}}and {n_{\text{t}}}-{\gamma _{{\text{max}}}}(\nu \leqslant 0.2)
![]()
图 13 {n_{\text{t}}}-{\mu _\Delta }和{n_{\text{t}}}-\mu _{\text{ε}}关系(\nu \leqslant 0.2)
Figure 13. Relationship s of {n_{\text{t}}}-{\mu _\Delta } and {n_{\text{t}}}-\mu _{\text{ε}}(\nu \leqslant 0.2)
表 1 三种节点单元模型计算结果与试验结果对比
Table 1 Comparison of the simulated results of three joint models with experimental results
试件名称 {K}_{\text{P}-\text{m}}=({P}_{\text{max}}^{模拟}/{P}_{\text{max}}^{试验}) {K}_{\varDelta -\text{m}}=({\varDelta }_{\text{max}}^{模拟}/{\varDelta }_{\text{max}}^{试验}) {K}_{\tau -\text{m}}=({\tau }_{\text{max}}^{模拟}/{\tau }_{\text{max}}^{试验}) MBCJE BCJE1 BCJE2 MBCJE BCJE1 BCJE2 MBCJE BCJE1 BCJE2 J-7 0.89 0.87 1.06 1.14 0.61 1.12 0.97 0.79 0.94 J-8 0.93 0.91 1.09 1.21 0.84 1.23 1.09 0.90 1.02 J-9 0.85 0.84 0.93 1.02 0.72 1.25 0.93 0.77 0.86 J-10 0.95 0.96 1.03 1.13 0.98 1.48 1.06 0.89 0.93 J-15 0.94 0.9 1.04 1.46 0.99 1.11 1.11 0.80 0.94 J-16 0.91 0.94 1.13 1.26 1.00 0.99 1.04 0.83 0.98 平均值 0.91 0.90 1.05 1.20 0.86 1.20 1.03 0.83 0.94 变异系数 0.039 0.049 0.065 0.12 0.19 0.14 0.068 0.065 0.057 注：表中上标“模拟”表示有限元计算结果，“试验”表示试验结果。 
下载: 导出CSV
-
[1] 霍林生, 李宏男, 肖诗云, 等. 汶川地震钢筋混凝土框架结构震害调查与启示[J]. 大连理工大学学报, 2009, 49(5): 718 − 723. doi: 10.7511/dllgxb200905016 HUO Linsheng, LI Hongnan, XIAO Shiyun, et al. Earthquake damage investigation and analysis of reinforced concrete frame structures in Wenchuan earthquake [J]. Journal of Dalian University of Technology, 2009, 49(5): 718 − 723. (in Chinese) doi: 10.7511/dllgxb200905016
[2] ZHAO B, TAUCER F, ROSSETTO T. Field investigation on the performance of building structures during the 12 May 2008 Wenchuan earthquake in China [J]. Engineering Structures, 2009, 31(8): 1707 − 1723. doi: 10.1016/j.engstruct.2009.02.039
[3] 许伟志, 王曙光, 贲驰, 等. 考虑两类装配式节点非线性行为的框架结构响应分析[J]. 工程力学, 2022, 39(7): 158 − 169. doi: 10.6052/j.issn.1000-4750.2021.04.0270 XU Weizhi, WANG Shuguang, BEN Chi, et al. Response analysis of frame structures considering the nonlinear behavior of two types of precast joints [J]. Engineering Mechanics, 2022, 39(7): 158 − 169. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.04.0270
[4] PAULAY T, PARK R, PREISTLEY M J N. Reinforced concrete beam-column joints under seismic actions [J]. Journal of American Concrete Institute, 1978, 75(11): 585 − 593.
[5] KITAYAMA K, ASAKURA H, OTANI S, et al. Earthquake resistant design criteria for reinforced concrete interior beam-column joints [C]. Trans JCI, 1988, 10: 281 − 288.
[6] KIM J, LAFAVE J M. Key influence parameters for the joint shear behaviour of reinforced concrete (RC) beam–column connections [J]. Engineering Structures, 2007, 29(10): 2523 − 2539. doi: 10.1016/j.engstruct.2006.12.012
[7] HEGGER J, SHERIF A, ROESER W. Nonseismic design of beam-column joint [J]. ACI Structural Journal, 2003, 100(5): 654 − 664.
[8] 朱爱萍. 高轴压比高剪压比框架矩形及圆形柱中间层中节点抗震性能试验研究[D]. 重庆: 重庆大学, 2005. ZHU Aiping. Experimental research on the seismic behavior of rectangular and circular column interior joint with high shear-compression ratio and high axial load ration in the frame [D]. Chongqing: Chongqing University, 2005. (in Chinese)
[9] 朱孝辉. 混凝土框架节点滞回性能研究[D]. 长沙: 湖南大学, 2017. ZHU Xiaohui. Research on hysteretic performance of concrete frame joints [D]. Changsha: Hunan University, 2017. (in Chinese)
[10] SECKIN M, UZUMERI S M. Exterior beam-column joints in reinforced concrete frames [C]. Proceedings of the 7th World Conference on Earthquake Engineering. Istanbul, Turkey, 1980: 183 − 190.
[11] MEINHEIT D F, JIRSA J O. The shear strength of reinforced concrete beam-column joints [R]. Structures Research Laboratory, 1977.
[12] KAKU T, ASAKUSA H, AOKI M. Ductility estimation of exterior beam-column subassemblages in reinforced concrete frames [J]. Journal of Structural and Construction Engineering (Transactions of AIJ), 1989, 401: 87 − 96. doi: 10.3130/aijsx.401.0_87
[13] SCOTT R , HAMIL S J, BAGLIN P S. Behavior of high-strength concrete beam-column connections [J]. ACI Special Publications, 1999, 186: 699 − 714.
[14] 框架节点专题研究组. 低周反复荷载作用下钢筋混凝土框架梁柱节点核心区抗剪强度的试验研究[J]. 建筑结构学报, 1983, 4(6): 1 − 17. Research Group on Frame Joints. Shear strength of reinforced concrete beam-column joints under low reversed cyclic loading [J]. Journal of Building Structures, 1983, 4(6): 1 − 17. (in Chinese)
[15] 熊学玉, 谢一凡, 姚刚峰. 基于修正的软化拉压杆模型的RC框架边节点受剪性能研究[J]. 工程力学, 2022, 39(6): 55 − 71. doi: 10.6052/j.issn.1000-4750.2021.03.0192 XIONG Xueyu, XIE Yifan, YAO Gangfeng. Study on shear behaviour of exterior reinforced concrete beam-column joints based on modified softened strut and tie model [J]. Engineering Mechanics, 2022, 39(6): 55 − 71. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.03.0192
[16] 傅剑平. 钢筋混凝土框架节点抗震性能与设计方法研究[D]. 重庆: 重庆大学, 2002. FU Jianping. Seismic behaviour and design of joints in a reinforced concrete frame [D]. Chongqing: Chongqing University, 2002. (in Chinese)
[17] 傅剑平, 张川, 陈滔, 等. 钢筋混凝土抗震框架节点受力机理及轴压比影响的试验研究[J]. 建筑结构学报, 2006, 27(3): 67 − 77. doi: 10.3321/j.issn:1000-6869.2006.03.009 FU Jianping, ZHANG Chuan, CHEN Tao, et al. Experimental investigation of shear mechanism and effect of axial-compression ratio on joints in earthquake-resistant reinforced concrete frames [J]. Journal of Building Structures, 2006, 27(3): 67 − 77. (in Chinese) doi: 10.3321/j.issn:1000-6869.2006.03.009
[18] 王丽萍, 罗文文, 刘思危, 等. 考虑梁轴向约束效应的RC梁柱节点受力机理及抗震性能试验研究[J]. 工程力学, 2020, 37(2): 159 − 167, 191. doi: 10.6052/j.issn.1000-4750.2019.03.0130 WANG Liping, LUO Wenwen, LIU Siwei, et al. Experimental investigation of beam elongation effects on the mechanism and seismic performance of RC frame joints [J]. Engineering Mechanics, 2020, 37(2): 159 − 167, 191. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.03.0130
[19] GB 50010−2010, 混凝土结构设计规范[S]. 北京: 中国建筑工业出版社, 2011. GB 50010−2010, Code for design of concrete structures [S]. Beijing: China Architecture & Building Press, 2011. (in Chinese)
[20] LOWES L N, ALTOONTASH A. Modeling reinforced-concrete beam-column joints subjected to cyclic loading [J]. Journal of Structural Engineering, 2003, 129(12): 1686 − 1697. doi: 10.1061/(ASCE)0733-9445(2003)129:12(1686)
[21] MITRA N, LOWES L N. Evaluation, calibration, and verification of a reinforced concrete beam-column joint model [J]. Journal of Structural Engineering, 2007, 133(1): 105 − 120. doi: 10.1061/(ASCE)0733-9445(2007)133:1(105)
[22] MAZZONI S, MCKENNA F, SCOTT M H, et al. OpenSees command language manual [M]. Berkeley: Pacific Earthquake Engineering Research Center, 2022.
[23] HWANG H J, EOM T S, PARK H G. Design considerations for interior RC beam–column joint with additional bars [J]. Engineering Structures, 2015, 98: 1 − 13. doi: 10.1016/j.engstruct.2015.04.021
[24] 王国林, 孟少平. 基于改进拉压杆模型的PC框架节点抗剪强度预测[J]. 建筑结构, 2013, 43(19): 38 − 41,53. WANG Guolin, MENG Shaoping. Shear strength prediction of prestressed concrete beam-column joints based on modified strut-and-tie model [J]. Building Structure, 2013, 43(19): 38 − 41,53. (in Chinese)
[25] 邢国华, 刘伯权, 牛荻涛. 钢筋混凝土框架中节点受剪承载力计算的修正软化拉压杆模型[J]. 工程力学, 2013, 30(8): 60 − 66. doi: 10.6052/j.issn.1000-4750.2012.03.0184 XING Guohua, LIU Boquan, NIU Ditao. Shear strength of reinforced concrete frame joints using modified softened strut-and-tie model [J]. Engineering Mechanics, 2013, 30(8): 60 − 66. (in Chinese) doi: 10.6052/j.issn.1000-4750.2012.03.0184
[26] ACI 318-14, Building code requirements for structural concrete and commentary [S]. Farmington Hills, MI: American Concrete Institute, 2014.
[27] 董俊宏, 杨红, 赵雯桐. 混凝土框架中间节点改进斜压杆模型及定参方法[J]. 地震工程与工程振动, 2017, 37(1): 155 − 164. doi: 10.13197/j.eeev.2017.01.155.dongjh.020 DONG Junhong, YANG Hong, ZHAO Wentong. Improved diagonal strut model and parameters determination for interior joints in RC frames [J]. Earthquake Engineering and Engineering Dynamics, 2017, 37(1): 155 − 164. (in Chinese) doi: 10.13197/j.eeev.2017.01.155.dongjh.020
[28] 刘春玲. 考虑轴力影响的RC梁柱中间层中节点受力性能有限元模拟分析[D]. 重庆: 重庆大学, 2022. LIU Chunling. Finite element simulation analysis of mechanical performance of RC beam-column joint considering the influence of axial force [D]. Chongqing: Chongqing University, 2022. (in Chinese)
[29] ZHAO W T, YANG H, CHEN J F, et al. A proposed model for nonlinear analysis of RC beam-column joints under seismic loading [J]. Engineering Structures, 2019, 180: 829 − 843. doi: 10.1016/j.engstruct.2018.09.068
[30] SCOTT B D, PARK R, PRIESTLEY M J N. Stress-strain behavior of concrete confined by overlapping hoops at low and high strain rates [J]. ACI Journal, 1982, 79(1): 13 − 27.
[31] 赵雯桐. 考虑节点非弹性变形特征的RC梁柱节点抗震性能试验及有限元模型研究[D]. 重庆: 重庆大学, 2019. ZHAO Wentong. Study on seismic behavior and finite element model of RC beam-column joint with the consideration of joint inelastic deformations [D]. Chongqing: Chongqing University, 2019. (in Chinese)
[32] 武秀莹. 配置500级纵筋的框架中间层中节点抗震性能试验及设计方法研究[D]. 重庆: 重庆大学, 2008. WU Xiuying. Experimental and design methodological research for the seismic behavior of interior joint with 500MPa longitudinal bar [D]. Chongqing: Chongqing University, 2008. (in Chinese)
[33] 钱稼茹, 冯宝锐. 不同抗震等级钢筋混凝土柱抗震性能试验研究[J]. 建筑结构学报, 2014, 35(7): 105 − 114. QIAN Jiaru, FENG Baorui. Experimental study on seismic behavior of different seismic grade RC columns [J]. Journal of Building Structures, 2014, 35(7): 105 − 114. (in Chinese)
[34] 张国军, 吕西林, 刘伯权. 钢筋混凝土框架柱在轴压比超限时抗震性能的研究[J]. 土木工程学报, 2006, 39(3): 47 − 54. doi: 10.3321/j.issn:1000-131X.2006.03.007 ZHANG Guojun, LYU Xilin, LIU Boquan. Seismic behavior of reinforced concrete frame columns with excessive axial compression ratios [J]. China Civil Engineering Journal, 2006, 39(3): 47 − 54. (in Chinese) doi: 10.3321/j.issn:1000-131X.2006.03.007
[35] 赵作周, 韩文龙, 钱稼茹, 等. 梁纵筋锚固板锚固装配整体式梁柱边节点抗震性能试验[J]. 哈尔滨工业大学学报, 2016, 48(12): 19 − 27. doi: 10.11918/j.issn.0367-6234.2016.12.002 ZHAO Zuozhou, HAN Wenlong, QIAN Jiaru, et al. Seismic behavior of assembled monolithic beam-column exterior joints with beam longitudinal rebars anchored by heads [J]. Journal of Harbin Institute of Technology, 2016, 48(12): 19 − 27. (in Chinese) doi: 10.11918/j.issn.0367-6234.2016.12.002
[36] 莫林辉. 节点区非弹性变形的统计规律及对RC框架强震反应的影响[D]. 重庆: 重庆大学, 2013. MO Linhui. Statistical law of inelastic deformation in beam-column joint and its effect on the seismic response of RC frame [D]. Chongqing: Chongqing University, 2013. (in Chinese)
计量
- 文章访问数: 77
- HTML全文浏览量: 18
- PDF下载量: 21
