STUDY ON FLEXURAL PERFORMANCE OF REINFORCED RC BEAMS STRENGTHENED WITH PRESTRESSED CARBON TEXTILE REINFORCED CONCRETE PLATES
-
摘要:
为了提高既有RC梁的抗弯性能,提升施工效率、减少加固现场湿作业,提出了一种预应力碳纤维织物增强混凝土(Prestressed Carbon Textile Reinforced Concrete, P-TRC)板加固RC梁的方法,其中板梁之间采用射钉连接。设计了3种对比工况和6种加固工况,进行四点弯曲加载试验,分析了P-TRC板的织物层数、梁的配筋率和混凝土强度等级对梁破坏形态、裂缝分布及宽度和承载力等影响。试验结果表明:P-TRC板加固RC梁的方式能显著提升试验梁的承载力和抗弯刚度,并降低裂缝宽度,其中开裂荷载提升28.7%~55.9%、屈服荷载提升8.06%~23.90%;P-TRC板的织物层数对梁抗弯性能影响较大,随着织物层数的增加,试验梁的抗弯性能越好,更能有效地抑制裂缝发展;提高梁的配筋率,加固梁的抗弯性均有所提升,但加固效果会减弱。最后基于正截面抗弯承载力理论,并考虑了P-TRC板的应变滞后,建立了加固梁抗弯承载力计算公式,该公式的理论计算值与试验值吻合较好。
-
关键词:
- 钢筋混凝土(RC)梁 /
- 试验研究 /
- 抗弯性能 /
- P-TRC板 /
- 射钉连接
Abstract:Proposed is a method for retrofitting RC beams prestressed by carbon textile reinforced concrete (Prestressed Carbon Textile Reinforced Concrete,P-TRC) plates. The plates and beams are connected by nails to improve the construction efficiency and to reduce the wet work. Three comparison applications and six reinforcement applications were designed to conduct experimental tests. Analyzed were the effects of fabric layers of P-TRC plates, the reinforcement ratio of the beam, and the strength level of concrete on the bending behavior of the beam. Compared were the failure form, crack distribution, and bearing capacity of all applications. The bearing capacity and flexural rigidity of beams were significantly improved by this method. The crack loading was increased by 28.7~55.9%. The yield loading was increased by 8.06~23.9%. The crack width was reduced by 30.2~41.1%. This method is more effective as the number of fabric layers of P-TRC plates increases. The bending resistances of the beams are increased as the reinforcement ratio increase, but the retrofitting effect of this method is diminished. Finally, the formula for calculating the flexural loading capacity of a reinforced beam is established upon the theory of bending capacity of normal section and upon the consideration of the strain hysteresis of P-TRC plates. The results obtained using this formula agreed well with the experimental ones.
-
Keywords:
- RC beam /
- experimental study /
- flexural resistance /
- P-TRC plates /
- nail connection
-
近年来,由于织物增强混凝土(The Textile Reinforced Concrete,TRC)具有强度高、耐高温及耐腐蚀性能好等优点,在混凝土结构的加固工程中得到广泛应用。与FRP材料不同,TRC与基材间有更好粘结性和协调性,而且具有抗老化和耐火等优点[1],亦可适用于环境比较复杂的结构中[2],国内外诸多学者已将TRC应用于构件的抗弯加固中[3-4]。
TRC加固方式以层铺法为主,即先在加固区涂抹砂浆,然后粘贴纤维织物网,最后再涂抹一层砂浆,此施工方法无需模板且有多种粘贴方式,分为封闭缠绕粘贴、U形粘贴和侧面粘贴[5],但均存在织物不平整的问题。荀勇等[6-7]通过试验研究发现TRC薄板加固RC梁可以有效地提高梁的抗弯性能,并解决了织物不平整的问题,但在配网率较高时,界面会发生脱粘现象。国外学者通过试验发现当TRC与混凝土界面发生剥离破坏时,织物较完整且未发生断裂,表明织物利用率不高[8-9]。为了提高织物的利用率,杜运兴等[10-11]设计特定装置,对TRC材料施加预应力并将其预制成板材,使TRC在板中处于平直状态,织物强度得到充分利用。随后被应用在加固石楼板中[3],通过对其进行四点弯曲试验,结果表明能大幅提高其弯性能。但板与梁接触面还需要凿毛及润湿处理,影响施工效率,因此,加固方式还需进一步改进。
当前,诸多学者在加固理论分析和计算方面也进行了大量研究[12-14],徐世烺等[15]通过在TRC加固梁新老混凝土界面植入抗剪销钉提出了梁破坏时弯矩的计算方法。尹世平等[16]提出了纤维编织网-ECC加固梁的抗弯承载力计算公式,并基于该公式发现梁极限弯矩对ECC高度和纤维编织网层数的敏感性较低。周芬采用无机砂浆将TRC复合板粘贴在梁的受拉区,在板材加固段缠绕CFRP布提高TRC板端部锚固[10-11]效果并提出了加固梁正截面受弯承载力的理论计算方法及挠度计算。LIU等[17]对FRP筋轻骨料混凝土梁的裂缝宽度开展理论分析,建立了掺钢纤维与未掺纤维试件使用阶段最大裂缝宽度计算模型。但在实际环境下构件所受外荷载难以准确获知,无法直接根据荷载进行裂缝宽度计算。为此,何浩祥等[18]基于粘结滑移理论,提出基于构件挠度来计算裂缝宽度的方法及流程,但仅适用于纤维编织网及改性混凝土加固梁的方法。
针对上述存在的不足,本课题组提出了预应力碳纤维织物增强混凝土(P-TRC)板通过射钉连接加固RC梁的方法,此改进方法不仅能充分发挥板材的性能,还有施工便捷、缩短施工周期和减少现场湿作业的特点。本文开展了P-TRC板加固RC梁抗弯性能试验,分析了P-TRC板织物层数、纵筋配筋率和混凝土强度对RC梁抗弯性能的影响,并提出了抗弯承载力公式。
1 试验概况
1.1 试件设计
试验共设计了18根钢筋混凝土梁,分为9种工况,其中有3种对比工况和6种加固工况,每种工况包含2根梁。梁总长度为3200 mm,计算长度为3000 mm,截面尺寸(b×h)为200 mm×400 mm的矩形,混凝土保护层厚度为20 mm。受压区布置2根HPB300,直径为10 mm的钢筋;受拉区布置2根HRB400,直径为18 mm、20 mm的钢筋;箍筋采用HPB300,直径为10 mm的钢筋,纯弯段间距为200 mm,弯剪段间距为90 mm。梁尺寸及截面配筋如图1所示,具体参数及工况如表1所示。其中P-TRC板的织物层数和试验梁的配筋率通过参考文献[11]中的用量和《混凝土结构设计规范》[19]进行设计,为避免发生超筋破坏,织物层数控制在合理范围,并按照一定梯度设计(本文采用一层和两层碳纤维织物网)。
表 1 试件设计参数及工况Table 1. Test piece design parameters and working conditions工况 试件
编号织物铺设
层数纵筋直径/
mm配筋率/
%混凝土
强度数量 对比工况 B0 − 18 0.70 C30 2 B1 − 20 0.87 C30 2 B2 − 18 0.70 C40 2 加固工况 B0-1 1 18 0.70 C30 2 B0-2 2 18 0.70 C30 2 B1-1 1 20 0.87 C30 2 B1-2 2 20 0.87 C30 2 B2-1 1 18 0.70 C40 2 B2-2 2 18 0.70 C40 2 1.2 材料参数
根据规范《金属材料拉伸试验第1部分:室温试验方法》[20]进行钢筋材性试验,钢筋受拉屈服强度和极限强度实测值见表2。混凝土采用商品混凝土,试验中用到C30和C40两种混凝土等级,材料性能按照《混凝土结构设计规范》[19]相关规定进行测试,其试块为边长150 mm的立方体,并养护28 d,如表3所示。碳纤维织物按标准《定向纤维增强聚合物基复合材料拉伸性能试验方法》[21]进行拉伸试验,其材料性能参数如表4所示。所用射钉为定制水泥钢钉,长度60 mm,直径为5 mm,剪切强度为980 MPa,韧性弯曲度大于75°。
表 2 钢筋力学性能Table 2. Mechanical properties of steel bars名称 直径/mm 屈服强度/MPa 极限强度/MPa 弹性模量/GPa 纵筋 10 420.38 583.95 200 18 467.24 623.34 201 20 480.43 657.47 203 箍筋 10 420.38 583.95 200 1.3 P-TRC板的制作及力学性能
P-TRC板的制作通过定制的预应力张拉装置完成,该装置内有浇筑板材的模具。首先将碳纤维束编制成网格为20 mm×18 mm的碳纤织物并将其裁剪为1800 mm×200 mm的网格布,随后涂刷无机胶,如图2所示。然后将制备好的低聚物增强混凝土倒入模具中,厚度约为10 mm。将碳纤维织物固定在张拉装置中,对其进行预应力调试,随后二次浇筑,若制作两层P-TRC板时,应在两层织物之间再次进行浇筑,厚度为2 mm,使其有良好的粘结性。随后进行预应力张拉,经过多次补张拉后,使每束碳纤维的预拉力水平维持在3.26 kN左右,即预应力度为60%,最后对其振捣密实。初步硬化后,将其取出并养护28 d。
表 3 混凝土及地聚物混凝土力学性能Table 3. Mechanical properties of concrete and geopolymer concrete材料种类 抗压强度/MPa 弹性模量/GPa 数量 混凝土 C30 24.26 30.1 3 C40 36.63 31.5 3 地聚物增强混凝土 24.23 31.2 3 表 4 碳纤维织物力学性能Table 4. Mechanical properties of carbon Textile试件类型 抗拉强度/MPa 弹性模量/
GPa极限应变/
με碳纤维织物 3123 208 15090 P-TRC板的单向拉伸性能直接影响加固梁的力学性能,由于P-TRC板承受的拉力主要由纤维网格承担[10],所以本构模型的参数与碳纤维织物保持一致,P-TRC板相关参数如表5所示。
表 5 P-TRC板相关参数Table 5. P-TRC plate related parameters名称 织物层数 厚度/mm Ap/mm2 Af/mm2 ρp/(%) P-TRC板 1 20 27 4000 0.68 2 22 54 4400 1.23 注:Ap为P-TRC板侧向截面积;Af为碳纤维织物侧向纤维束面积;ρp为P-TRC板配网率。 1.4 加固方案
用P-TRC板在梁底受拉区进行加固,长度取2800 mm,其中,P-TRC板的预应力度为60%。通过长度为60 mm的射钉相连接,采用等间距排布以达到均匀受力的效果,为防止P-TRC板脱离梁底,在端部进行了适当加密。所采用的射钉由射钉枪打入,考虑打入时射钉会造成周围混凝土损伤开裂,因此在射钉端部留有中间略鼓的垫圈,垫圈与钉帽之间设置橡胶材质缓冲垫,通过垫圈和缓冲垫来减少能量的输入从而减小射钉周围混凝土的损伤,此外,射钉长度为60 mm因有垫圈的存在使其打入深度停留在保护层外5 mm左右,在保证锚固的同时,控制核心混凝土受到损伤最少,如图3所示。
加固梁的加固流程为:1)板材准备:裁剪对应尺寸的P-TRC板,在加工好的P-TRC板上进行网格绘制以便射钉定位,P-TRC板长边网格尺寸为100 mm,短边网格尺寸为50 mm、100 mm,在端部进行了适当的加密。
2)射钉连接:用射钉枪按网格定位进行P-TRC板的固定,为避免射钉打入时对内部碳纤维织物造成损害,在实际施工时会与射钉布置方案有1 mm~2 mm的偏差,确保射钉打在碳纤维织物网格内。
1.5 测点布置及加载方案
试验中主要测量跨中截面的应变、试验梁的挠度及裂缝宽度。试验梁跨中沿梁高方向布置5个应变片,梁顶布置2个应变片,纵筋及P-TRC板的中部和加载点对应的位置布置应变片。此外,在试验梁跨中及支座处布置位移计,以便测量跨中竖向挠度,如图4所示。
试验采用四点弯曲对称加载方式,通过分配梁将力分别作用在四等分加载点处,弯剪段长度为750 mm,纯弯段长度为1500 mm。在正式加载前进行预加载,以测定设备的工作性能。按照受力情况分三阶段分级加载:梁底开裂前、梁底开裂后至钢筋屈服前、钢筋屈服后至试件破坏,分级加载幅值分别为:10 kN/级、5 kN/级和10 kN/级。当试验梁出现顶部混凝土被压溃,荷载降低到峰值荷载的85%时停止加载,宣布破坏。
2 试验结果及分析
2.1 破坏现象及承载力
试验梁共有2种破坏形态,如图5所示。
1)第1类破坏形态。具体现象为纵向受拉钢筋屈服,继续增加外荷载,最终梁顶混凝土被压碎,所有的对比工况试验梁均属于这种破坏形态。
2)第2类破坏形态。具体现象为纵向受拉钢筋屈服,继续增加外荷载,P-TRC板突然断裂,承载力骤降,继续加载,随着变形的增加,P-TRC板从断裂处向两端进行剥落,部分射钉被剪断,最终梁顶混凝土被压碎,所有的加固工况试验梁均属于这种破坏形态。
各试验梁的承载力及破坏模式试验结果见表6,各工况的结果取两根梁试验值的平均值,其中,括号内为两根梁各自实测值。由表6可知,采用P-TRC板加固混凝土梁后,梁的开裂荷载、纵筋屈服荷载和P-TRC板断裂时的荷载都有一定程度的提高,但极限荷载提升不显著,其原因是在加固试验梁破坏前,P-TRC板发生断裂并退出工作,此时由原梁承担荷载。
表 6 试件试验结果Table 6. Test results of specimens工况 试件编号 Pcr/kN Py/kN Pd/kN Pu/kN 破坏形式 对比工况 B0 30.4(23.9/36.9) 216.5(201.6/231.4) − 246.6(238.5/254.7) R B1 39.6(36.7/42.5) 248.2(246.9/249.5) − 281.3(272.5/290.1) R B2 35.2(32.1/38.3) 231.1(210.6/251.6) − 265.3(258.2/272.4) R 加固工况 B0-1 41.6(37.9/45.3) 242.3(234.5/250.1) 267.2(259.1/275.3) 249.2(238.0/260.4) P+R B0-2 47.4(45.2/49.6) 268.2(259.6/276.8) 288.1(284.5/291.7) 243.1(233.9/252.3) P+R B1-1 50.5(46.8/54.2) 271.7(260.8/282.6) 306.3(300.8/311.8) 282.8(279.3/286.3) P+R B1-2 56.7(52.8/60.6) 288.4(286.5/290.3) 325.2(311.5/338.9) 276.2(270.9/281.5) P+R B2-1 45.3(42.2/48.4) 251.8(234.2/269.4) 283.6(267.0/300.2) 271.6(267.0/276.2) P+R B2-2 51.2(45.7/56.7) 278.9(273.6/284.2) 304.4(293.2/315.6) 259.9(255.1/264.7) P+R 注:R为梁的破坏为顶部混凝土压碎;P+R表示梁的破坏为P-TRC板部分断裂,顶部混凝土压碎;Pcr为开裂荷载;Py为屈服荷载;Pd为P-TRC板断裂时荷载;Pu为极限荷载。 对比仅改变配网率的试件(分为三组B0、B0-1、B0-2;B1、B1-1、B1-2;B2、B2-1、B2-2)试验数据,当织物层数由0层逐级增加至2层时,开裂荷载、屈服荷载和峰值荷载均有提高。其原因是,通过截面换算法,增加织物层数,等同加梁的配筋率,从而提高了截面的混凝土受压区高度,使梁的抵抗矩和惯性矩增大,促使承载力变高。对于第一组(B0、B0-1、B0-2)的试验数据,当织物层数由0层增加至1层时,试验梁的开裂荷载、屈服荷载、峰值荷载分别提高了36.8%、11.9%、8.4%,当织物层数由0层增加至2层时,试验梁的开裂荷载、屈服荷载、峰值荷载分别提高了55.9%、23.9%、16.8%,提高率随着织物层数的增加而增加,成正相关,其中开裂荷载提高最为明显。相比于第二组(B1、B1-1、B1-2)和第三组(B2、B2-1、B2-2)的试验数据,第一组数据提高效果最为显著,即在相同织物层数下,低配筋率、混凝土强度等级低的试件,开裂荷载和屈服荷载提升效果最佳。
对比仅改变纵筋配筋率的试件(分为两组B0-1、B1-1;B0-2、B1-2)试验数据,当配筋率增加时,低配网率试验梁(B0-1、B1-1)的开裂荷载、屈服荷载、峰值荷载分别提高了21.4%、12.1%、24.2%,相比于高配网率试验梁(B0-2、B1-2)提高的18.9%、7.8%、12.9%,提高更为明显。其原因为碳纤维织物网可有效分担受拉纵筋的应力,等同增加梁的配筋,通过比例计算可知,低配筋率试件的承载力提高比例最大。故在增加相同配筋率时,低配网率试验梁荷载提高最为明显。
对比仅改变混凝土强度的试件(分为两组B0-1、B2-1;B0-2、B2-2)试验数据,当混凝土强度由C30增加至C40时,虽然开裂荷载、屈服荷载和峰值荷载均有提高,但最高仅为8.9%、3.9%、7.1%,提高幅度较小,甚至可以忽略。其主要原因为提高混凝土强度,对混凝土受压区高度的增加较小,从而对承载力的影响较小。由此可见改变混凝土强度增益较小。
2.2 荷载-跨中挠度
依据试验所得数据进行分析,绘制出荷载-跨中挠度曲线,如图6所示。初期,P-TRC板与RC梁组合作用良好,荷载由受拉纵筋和P-TRC板共同承担。混凝土开裂后,试验梁的刚度减小,因此斜率略低于弹性阶段斜率,但总体高于对比梁。其原因为外荷载由受拉纵筋和P-TRC板共同承担,由于此阶段裂缝对试验梁刚度的影响较小,第二阶段依旧呈线性发展。随后,加固梁纵向受拉钢筋屈服,试件变形较大,承载力仍处于上升趋势,刚度显著降低,由于P-TRC板弹性模量较大,仍能承担部分弯矩,其刚度仍大于对比梁刚度,加固效果明显。继续增加外荷载,当P-TRC板达到极限应变时,发生断裂,承载力骤降。
图6(a)~图6(c)对比了仅不同配网率的荷载-跨中挠度曲线,在同级荷载下,随着织物层数的增加,跨中挠度减少。由此可见,梁截面刚度随织物层数的增加而增加,相比于图6(b)~图6(c),图6(a)刚度提升最明显,尤其是屈服后的刚度。其原因为钢筋屈服后,P-TRC板承担大部分荷载,并且P-TRC板弹性模量较大,使其变形缓慢。图6(e)对比了仅不同混凝土强度的荷载-跨中挠度曲线,在相同配网率下,提升混凝土强度,曲线斜率改变并不明显。上述现象的原因与前文2.1节原因相同,在此处不在阐述。
2.3 跨中截面应变
基于试验数据,绘制出四个典型试件的跨中应变沿梁高的分布图,如图7所示,在混凝土梁屈服前,跨中截面混凝土、受拉纵筋和P-TRC板的应变基本符合平截面假定,可以看出P-TRC板与梁连接良好,两者变形协调,未出现相对滑移。加载后期,P-TRC板应变略滞后于RC梁应变,织物层数越多,应变滞后越明显。这是由于加载过程中,随着变形增大,混凝土受拉区产生了若干裂缝,钢筋已屈服,梁整体刚度降低,此时主要由刚度大的P-TRC板承担,由于力传递通过板梁之间的射钉,射钉屈服,出现小幅度弯曲,所以P-TRC板与混凝土界面出现了相对滑移,最终导致P-TRC板变形略微滞后于RC梁,滑移出现在加载后期(P-TRC板断裂前),说明采用射钉连接具有一定的可靠性。由于加固梁最后破坏为P-TRC板断裂,因此板的应变在加载后期变化不大,保持在4000 με~5000 με,趋近于极限应变。
2.4 裂缝分布及宽度
试验中对比梁首先在纯弯段正应力最大处出现裂缝,随着荷载增加,试验梁在纯弯段相继出现多条裂缝,最早出现的裂缝宽度也在不断增加,随着变形的增加,剪弯区也出现多条裂缝。在钢筋屈服之后,跨中裂缝宽度不断增大形成几条主裂缝并向上延伸,最后梁顶受压区混凝土被压碎。
加固梁首先在纯弯段开裂,随后P-TRC板侧面出现裂缝,随着荷载的继续增加,相较于对比梁,加固梁的混凝土裂缝数量并没有减少,反而分布较为均匀,其裂缝产生位置与射钉位置基本一致。但发展速度较对比梁缓慢,其主要原因为P-TRC板承担了一部分外荷载,抑制了梁的变形,使得受拉区混凝土受拉变形发展缓慢。钢筋屈服后,P-TRC板的侧面及底部间隔一定距离出现多条裂缝,随后发生断裂。各试验梁纯弯段实测混凝土裂缝最大宽度(主裂缝宽度)随荷载的变化规律,如图8所示。
各试件在纯弯段的混凝土裂缝最大宽度与荷载的变化规律,如图9所示,其中裂缝最大宽度在试验梁屈服后停止测量。随着织物层数的增加,在同级荷载下裂缝宽度逐渐变小,这是因为P-TRC板弹性模量较大,随着织物层数的增加,约束梁的变形能力增强,抑制了裂缝的发展,从而减小裂缝宽度。相同配网率下,高配筋率的试验梁裂缝宽度明显小于低配筋率的试验梁;仅提高混凝土等级对裂缝的宽度影响较小。
3 抗弯承载力分析
3.1 基本假定与公式
① 加固梁跨中截面混凝土和受拉纵筋的应变基本符合平截面假定,而P-TRC板变形略滞后于构件整体变形;
② 忽略地聚物增强混凝土的影响及混凝土的抗拉强度;
③ 依据《混凝土结构设计规范》(GB 50010−2010)选取混凝土和钢筋的应力-应变关系,如式(1)和式(2)所示:
σc{fc[1−(1−εcε0)n],εc⩽ (1) {\sigma }_{{\rm{s}}}\left\{ \begin{aligned} & {E}_{\text{s}}{\varepsilon }_{{\rm{s}}},& {\varepsilon }_{{\rm{s}}}{\leqslant} {\varepsilon }_{{\rm{y}}}\qquad\;\\& {f}_{{\rm{y}}},& {\varepsilon }_{{\rm{y}}}<{\varepsilon }_{{\rm{s}}}{\leqslant} {\varepsilon }_{{\rm{u}}} \end{aligned}\right. (2) 式中:{\sigma _{\rm{c}}}为混凝土压应力;{\varepsilon _{\rm{c}}}为混凝土压应变;{f_{\rm{c}}}为混凝土轴心抗压强度; {\varepsilon _0} 为混凝土压应力达到{f_{\rm{c}}}时的压应变;{\varepsilon _{{\rm{cu}}}}为混凝土的极限压应变;{\sigma _{\rm{s}}}为钢筋应力;{\varepsilon _{\rm{s}}}为钢筋应变;{E_{\rm{s}}}为钢筋弹性模量;{\varepsilon _{\rm{y}}}为钢筋屈服应变;{\varepsilon _{\rm{u}}}为钢筋极限应变。
④ P-TRC板的应力-应变关系模型如式(3)所示:
{\sigma _{\rm{c}}} = \begin{array}{*{20}{c}} {{E_{\rm{s}}}{\varepsilon _{\rm{c}}}}&,\;{{\varepsilon _{\rm{c}}} \leqslant {\varepsilon _{{\rm{cu}}}}} \end{array} (3) 式中:{\sigma _{\rm{c}}}和{\varepsilon _{\rm{c}}}分别为P-TRC板的抗拉强度和应变值;{E_{\rm{s}}}为纤维织物弹性模量;{\varepsilon _{{\rm{cu}}}}为极限应变。
3.2 抗弯承载力理论推导
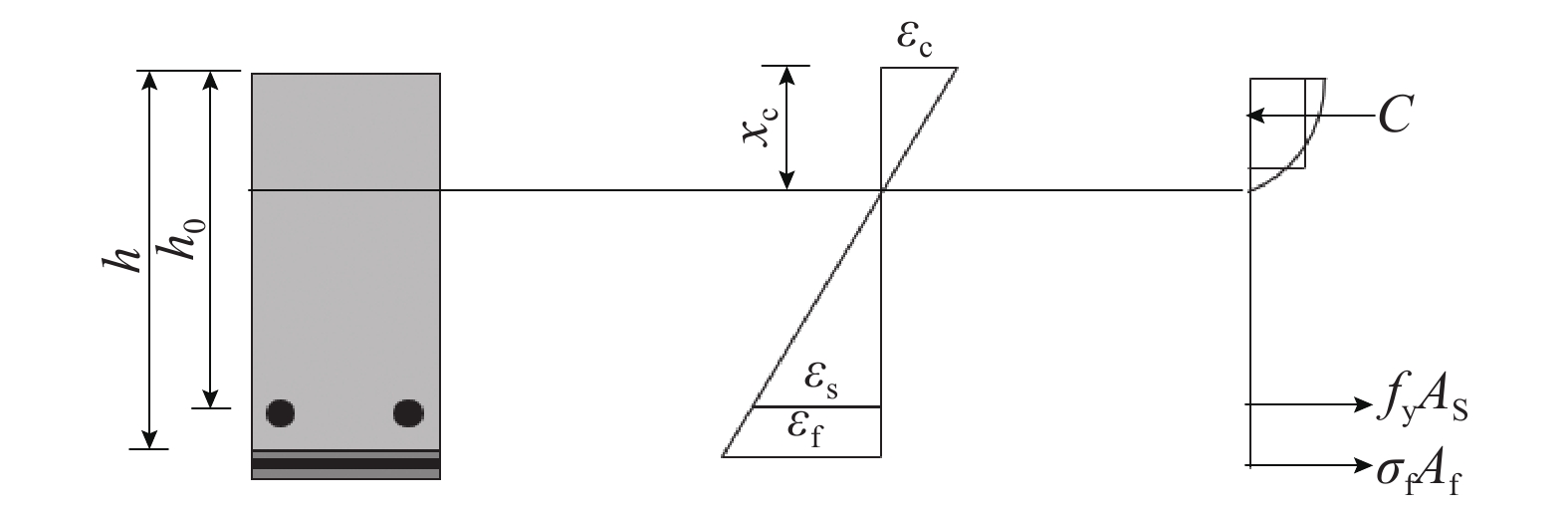
对加固梁破坏模式分析可知,P-TRC板断裂时,受拉纵筋已经屈服,但混凝土未被压碎,梁正截面抗弯承载力计算简图如图10所示。由于P-TRC板应变滞后于混凝土和钢筋的应变,对试验结果分析,P-TRC板应变滞后系数\lambda 取0.85,其中,\lambda 为加固梁峰值荷载状态下P-TRC板的实际应变与满足平截面假定时应变的比值。
由于P-TRC板在混凝土未达极限应变时发生破坏,在计算受压区合力C时, {\alpha _{\text{1}}} 和 {\beta _{\text{1}}} 不能用规范中的计算方法进行计算,依据文献[22-23]所给的公式进行计算:
{\alpha _{\text{1}}} = \frac{{0.9\ln \left( {1 + {\varepsilon _{\text{c}}}/\varepsilon _{\text{c}}'} \right)}}{{{\beta _{\text{1}}}{\varepsilon _{\text{c}}}/\varepsilon _{\text{c}}'}} (4) {\beta _{\text{1}}} = 2 - \frac{{4\left[ {{\varepsilon _{\text{c}}}/\varepsilon _{\text{c}}' - {{\arctan }}\left( {{\varepsilon _{\text{c}}}/\varepsilon _{\text{c}}'} \right)} \right]}}{{\left( {{\varepsilon _{\text{c}}}/\varepsilon _{\text{c}}'} \right)\ln \left( {1 + {\varepsilon _{\text{c}}}/\varepsilon _{\text{c}}'} \right)}} (5) \varepsilon _{\rm{c}}' = 1.71{f_{\rm{c}}}/{E_{\rm{c}}} (6) 力平衡条件得;
{x_{\rm{c}}} = \lambda \frac{{{f_{\rm{y}}}{A_{\rm{s}}} + {\sigma _{\rm{f}}}{A_{\rm{f}}}}}{{{\alpha _1}{\beta _1}{f_{\rm{c}}}b}} (7) 由于P-TRC板断裂较早,应变滞后系数M = {f_{\text{y}}}{A_{\text{s}}}\left( {{h_{\text{0}}} - \dfrac{{{\beta _{\text{1}}}{x_{\text{c}}}}}{2}} \right) + {\sigma _{\text{f}}}\lambda {A_{\text{f}}}\left( {h + \dfrac{{{h_{\text{m}}}}}{2} - \dfrac{{{\beta _{\text{1}}}{x_{\text{c}}}}}{2}} \right)仅影响混凝土受压区高度,故在计算混凝土受压区高度时,应对其进行削弱。
力矩平衡条件得;
M = {f_{\text{y}}}{A_{\text{s}}}\left( {{h_{\text{0}}} - \frac{{{\beta _{\text{1}}}{x_{\text{c}}}}}{2}} \right) + {\sigma _{\text{f}}}\lambda {A_{\text{f}}}\left( {h + \frac{{{h_{\text{m}}}}}{2} - \frac{{{\beta _{\text{1}}}{x_{\text{c}}}}}{2}} \right) (8) P = \frac{{2M}}{L} (9) 式中:P为峰值荷载理论值;L为加载点到支座的距离; {\varepsilon _c} 为混凝土极限压应变; {h_{\text{m}}} 为P-TRC板薄板的厚度; {x_{\text{c}}} 为换算截面受压区高度; {A_{\text{f}}} 为纤维织物截面面积。
3.3 计算值与试验值对比
表7为试验梁的峰值荷载理论值Pdc与试验值Pdt的对比。加固梁抗弯承载力按上述公式所计算的理论值与试验值结果接近。因此,该公式可用于指导P-TRC板加固混凝土梁的设计。
表 7 试件梁的理论值与试验值对比Table 7. Comparison of theoretical and test values of specimen beams试件编号 Pdc/kN Pdt/kN Pdc/Pdt B0-1 261.8 267.2 0.98 B0-2 274.9 288.1 0.95 B1-1 281.3 306.3 0.92 B1-2 292.1 325.2 0.89 B2-1 297.9 283.6 1.05 B2-2 321.3 304.4 1.06 注:Pdc为理论值;Pdt为试验值。 4 结论
本文开展了P-TRC板加固RC梁抗弯性能试验研究,根据试验现象和数据分析,考察了射钉的可靠性及抗弯性能的提升效果,并建立了抗弯承载力的计算方法,主要结论如下:
(1) 采用射钉将P-TRC板与梁底连接的方法加固RC梁,具有施工便捷、工期短等特点,能显著提升梁的开裂荷载、屈服荷载及刚度,并能有效的减小裂缝宽度。
(2) 加固梁开裂荷载、屈服荷载、峰值荷载和刚度均随织物层数、梁配筋率的增加而增加,成正相关。其中,梁的开裂荷载提高最为显著,而改变混凝土强度等级对梁抗弯性能的影响较小。
(3) 基于试验结果及理论分析,P-TRC板能有效分担梁受拉纵筋中的应力。在加载前期,满足平截面假定,但构件屈服后,P-TRC板略滞后于原梁变形。最后,提出了P-TRC板加固RC梁正截面抗弯承载力计算公式,且数据吻合良好。
(4) 本文连接方式仅采用射钉,相较于传统方式,简单快捷且具有一定的可靠性,但试验中加固梁裂缝均发生在射钉位置,出现应力集中现象。因此,连接界面应进行凿毛处理并加设砂浆粘结层,将会进一步减小射钉过程中对试件的损伤以及提高试件粘结强度。
(5) 本文仅考虑了P-TRC板的织物层数、梁的配筋率和混凝土强度等级三个工况,工况数量较少,具有一定的局限性,需进一步分析不同预应力度及不同射钉布置方案对试验结果的影响,并进行有限元模拟,为实际工程提供参考。
-
表 1 试件设计参数及工况
Table 1 Test piece design parameters and working conditions
工况 试件
编号织物铺设
层数纵筋直径/
mm配筋率/
%混凝土
强度数量 对比工况 B0 − 18 0.70 C30 2 B1 − 20 0.87 C30 2 B2 − 18 0.70 C40 2 加固工况 B0-1 1 18 0.70 C30 2 B0-2 2 18 0.70 C30 2 B1-1 1 20 0.87 C30 2 B1-2 2 20 0.87 C30 2 B2-1 1 18 0.70 C40 2 B2-2 2 18 0.70 C40 2 表 2 钢筋力学性能
Table 2 Mechanical properties of steel bars
名称 直径/mm 屈服强度/MPa 极限强度/MPa 弹性模量/GPa 纵筋 10 420.38 583.95 200 18 467.24 623.34 201 20 480.43 657.47 203 箍筋 10 420.38 583.95 200 表 3 混凝土及地聚物混凝土力学性能
Table 3 Mechanical properties of concrete and geopolymer concrete
材料种类 抗压强度/MPa 弹性模量/GPa 数量 混凝土 C30 24.26 30.1 3 C40 36.63 31.5 3 地聚物增强混凝土 24.23 31.2 3 表 4 碳纤维织物力学性能
Table 4 Mechanical properties of carbon Textile
试件类型 抗拉强度/MPa 弹性模量/
GPa极限应变/
με碳纤维织物 3123 208 15090 表 5 P-TRC板相关参数
Table 5 P-TRC plate related parameters
名称 织物层数 厚度/mm Ap/mm2 Af/mm2 ρp/(%) P-TRC板 1 20 27 4000 0.68 2 22 54 4400 1.23 注:Ap为P-TRC板侧向截面积;Af为碳纤维织物侧向纤维束面积;ρp为P-TRC板配网率。 表 6 试件试验结果
Table 6 Test results of specimens
工况 试件编号 Pcr/kN Py/kN Pd/kN Pu/kN 破坏形式 对比工况 B0 30.4(23.9/36.9) 216.5(201.6/231.4) − 246.6(238.5/254.7) R B1 39.6(36.7/42.5) 248.2(246.9/249.5) − 281.3(272.5/290.1) R B2 35.2(32.1/38.3) 231.1(210.6/251.6) − 265.3(258.2/272.4) R 加固工况 B0-1 41.6(37.9/45.3) 242.3(234.5/250.1) 267.2(259.1/275.3) 249.2(238.0/260.4) P+R B0-2 47.4(45.2/49.6) 268.2(259.6/276.8) 288.1(284.5/291.7) 243.1(233.9/252.3) P+R B1-1 50.5(46.8/54.2) 271.7(260.8/282.6) 306.3(300.8/311.8) 282.8(279.3/286.3) P+R B1-2 56.7(52.8/60.6) 288.4(286.5/290.3) 325.2(311.5/338.9) 276.2(270.9/281.5) P+R B2-1 45.3(42.2/48.4) 251.8(234.2/269.4) 283.6(267.0/300.2) 271.6(267.0/276.2) P+R B2-2 51.2(45.7/56.7) 278.9(273.6/284.2) 304.4(293.2/315.6) 259.9(255.1/264.7) P+R 注:R为梁的破坏为顶部混凝土压碎;P+R表示梁的破坏为P-TRC板部分断裂,顶部混凝土压碎;Pcr为开裂荷载;Py为屈服荷载;Pd为P-TRC板断裂时荷载;Pu为极限荷载。 表 7 试件梁的理论值与试验值对比
Table 7 Comparison of theoretical and test values of specimen beams
试件编号 Pdc/kN Pdt/kN Pdc/Pdt B0-1 261.8 267.2 0.98 B0-2 274.9 288.1 0.95 B1-1 281.3 306.3 0.92 B1-2 292.1 325.2 0.89 B2-1 297.9 283.6 1.05 B2-2 321.3 304.4 1.06 注:Pdc为理论值;Pdt为试验值。 -
[1] 刘赛, 朱德举, 李安令. 织物增强混凝土的研究与应用进展[J]. 建筑科学与工程学报, 2017, 34(5): 134 − 146. LIU Sai, ZHU Deju, LI Anling. Research and application progress of textile reinforced concrete [J]. Journal of Architecture and Civil Engineering, 2017, 34(5): 134 − 146. (in Chinese)
[2] SCHLADITZ F, FRENZEL M, EHLIG D, et al. Bending load capacity of reinforced concrete slabs strengthened with textile reinforced concrete [J]. Engineering Structures, 2012, 40: 317 − 326. doi: 10.1016/j.engstruct.2012.02.029
[3] 张丰宇, 何佰昭, 吴应雄, 等. CFRP板加固既有石楼板抗弯性能试验研究[J]. 工程力学, 2024. doi: 10.6052/j.issn.1000-4750.2022.08.0722,2023-08-15 ZHANG Fengyu, HE Baizhao, WU Yingxiong, et al. Experimental study on flexural behavior of existing stone slabs strengthened by CFRP plate [J]. Engineering Mechanics, 2024. (in Chinese) doi: 10.6052/j.issn.1000-4750.2022.08.0722,2023-08-15
[4] 尹世平, 盛杰, 贾申, 等. TRC加固RC梁的弯曲疲劳破坏过程和应变发展的试验研究[J]. 工程力学, 2015, 32(增刊 1): 142 − 148. doi: 10.6052/j.issn.1000-4750.2014.04.S010 YIN Shiping, SHENG Jie, JIA Shen, et al. Experimental study on bending fatigue damage and strain development of RC beam strengthened with TRC [J]. Engineering Mechanics, 2015, 32(Suppl 1): 142 − 148. (in Chinese) doi: 10.6052/j.issn.1000-4750.2014.04.S010
[5] CECS146−2003, 碳纤维片材加固混凝土结构技术规程[S]. 北京: 中国计划出版社, 2003. CECS146−2003, Technical specification for strengthening concrete structures with carbon fiber reinforced polymer laminate [S]. Beijing: China Planning Press, 2003. (in Chinese)
[6] 荀勇, 支正东, 张勤. 织物增强混凝土薄板加固钢筋混凝土梁受弯性能试验研究[J]. 建筑结构学报, 2010, 31(3): 70 − 76. XUN Yong, ZHI Zhengdong, ZHANG Qin. Experimental research on flexural behavior of reinforced concrete beams strengthened with textile reinforced concrete sheets [J]. Journal of Building Structures, 2010, 31(3): 70 − 76. (in Chinese)
[7] 荀勇, 孙伟, REINHARDT H W. 碳纤维织物增强混凝土薄板的界面粘结性能试验[J]. 东南大学学报(自然科学版), 2005, 35(4): 593 − 597. XUN Yong, SUN Wei, REINHARDT H W. Experiment on interface bonding performance of carbon textile reinforced concrete sheets [J]. Journal of Southeast University (Natural Science Edition), 2005, 35(4): 593 − 597. (in Chinese)
[8] OMBRES L. Debonding analysis of reinforced concrete beams strengthened with fibre reinforced cementitious mortar [J]. Engineering Fracture Mechanics, 2012, 81: 94 − 109. doi: 10.1016/j.engfracmech.2011.06.012
[9] OMBRES L. Flexural analysis of reinforced concrete beams strengthened with a cement based high strength composite material [J]. Composite Structures, 2011, 94(1): 143 − 155. doi: 10.1016/j.compstruct.2011.07.008
[10] 周芬, 徐文, 杜运兴. TRC板增强钢筋混凝土梁的抗弯性能[J]. 中南大学学报(自然科学版), 2018, 49(1): 183 − 191. ZHOU Fen, XU Wen, DU Yunxing. Flexural behavior of RC beams strengthened with TRC plates [J]. Journal of Central South University (Science and Technology), 2018, 49(1): 183 − 191. (in Chinese)
[11] 周芬, 陈小晔, 杜运兴, 等. 预拉纤维复合板增强梁抗弯性能研究[J]. 华中科技大学学报(自然科学版), 2019, 47(1): 60 − 66. ZHOU Fen, CHEN Xiaoye, DU Yunxing, et al. Study on flexural behavior of beams strengthened with prestressed fabric reinforced cementitious plates [J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2019, 47(1): 60 − 66. (in Chinese)
[12] 彭飞, 薛伟辰. FRP筋混凝土T形和矩形截面梁抗弯承载力计算方法[J]. 工程力学, 2022, 39(2): 76 − 84, 122. doi: 10.6052/j.issn.1000-4750.2020.12.0002 PENG Fei, XUE Weichen. Method of calculating the flexural strength of FRP reinforced concrete T-shaped and rectangular beams [J]. Engineering Mechanics, 2022, 39(2): 76 − 84, 122. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.12.0002
[13] 张书颖, 陈适之, 韩万水, 等. 基于集成学习的FRP加固混凝土梁抗弯承载力预测研究[J]. 工程力学, 2022, 39(8): 245 − 256. doi: 10.6052/j.issn.1000-4750.2021.06.0422 ZHANG Shuying, CHEN Shizhi, HAN Wanshui, et al. Study on prediction of FRP strengthened reinforced concrete beam’s moment bearing capacity based on ensemble learning algorithm [J]. Engineering Mechanics, 2022, 39(8): 245 − 256. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.06.0422
[14] 钱辉, 陈程, 张庆元, 等. 自修复SMA/ECC复合材料加固RC梁受弯性能试验研究[J]. 工程力学, 2023, 40(6): 73 − 84. doi: 10.6052/j.issn.1000-4750.2021.11.0871 QIAN Hui, CHEN Cheng, ZHANG Qingyuan, et al. Experimental study on flexural behavior of RC beam strengthened with self-repairing SMA/ECC composites materials [J]. Engineering Mechanics, 2023, 40(6): 73 − 84. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.11.0871
[15] 徐世烺, 尹世平, 蔡新华. 纤维编织网增强混凝土加固钢筋混凝土梁受弯性能研究[J]. 土木工程学报, 2011, 44(4): 23 − 34. doi: 10.15951/j.tmgcxb.2011.04.012 XU Shilang, YIN Shiping, CAI Xinhua. Investigation on the flexural behavior of reinforced concrete beam strengthened with textile-reinforced concrete [J]. China Civil Engineering Journal, 2011, 44(4): 23 − 34. (in Chinese) doi: 10.15951/j.tmgcxb.2011.04.012
[16] 盛杰, 尹世平, 裴浩. 纤维编织网-ECC加固RC梁受弯性能试验[J]. 中国公路学报, 2022, 35(9): 287 − 297. doi: 10.19721/j.cnki.1001-7372.2022.09.022 SHENG Jie, YIN Shiping, PEI Hao. Experimental study on flexural behavior of RC beams strengthened with textile and ECC [J]. China Journal of Highway and Transport, 2022, 35(9): 287 − 297. (in Chinese) doi: 10.19721/j.cnki.1001-7372.2022.09.022
[17] LIU X, SUN Y J, WU T, et al. Flexural cracks in steel fiber-reinforced lightweight aggregate concrete beams reinforced with FRP bars [J]. Composite Structures, 2020, 253: 112752. doi: 10.1016/j.compstruct.2020.112752
[18] 程时涛, 何浩祥, 程扬, 等. 纤维编织网及改性混凝土增强RC梁性能分析和裂缝宽度计算[J]. 工程力学, 2024. doi: 10.6052/j.issn.1000-4750.2022.12.1088. CHENG Shitao, HE Haoxiang, CHENG Yang, et al. Performance analysis and crack width calculation of RC beam strengthened with textile and modified concrete [J]. Engineering Mechanics, 2024. (in Chinese) doi: 10.6052/j.issn.1000-4750.2022.12.1088.
[19] GB 50010−2010, 混凝土结构设计规范[S]. 北京: 中国建筑工业出版社, 2011. GB 50010−2010, Code for design of concrete structures [S]. Beijing: China Architecture & Building Press, 2011. (in Chinese)
[20] 高怡斐, 梁新帮, 邓星临. 《<金属材料拉伸试验第1部分: 室温试验方法>实施指南》[J]. 品牌与标准化, 2014(18): 95. GAO Yifei, LIANG Xinbang, DENG Xinglin. Implementation guide for the tensile test of metallic materials part 1: Room temperature test methods [J]. Brand & Standardization, 2014(18): 95. (in Chinese)
[21] GB/T 3354−2014, 定向纤维增强聚合物基复合材料拉伸性能试验方法[S]. 北京: 中国标准出版社, 2015. GB/T 3354−2014, Test method for tensile properties of orientation fiber reinforced polymer matrix composite materials [S]. Beijing: Standards Press of China, 2015. (in Chinese)
[22] MILLER B, NANNI A. Bond between CFRP sheets and concrete materials and construction [C]// Proceedings of the Fifth ASCE Materials Engineering Congress. Cincinnati: American Society of Civil Engineers, 1999: 240 − 247.
[23] 邓朗妮, 康侃, 燕柳斌, 等. 侧贴预应力碳纤维板加固混凝土梁受弯承载力计算方法研究[J]. 建筑结构学报, 2011, 32(4): 95 − 100. DENG Langni, KANG Kan, YAN Liubin, et al. Flexural capacity analysis for strengthened concrete beams side-bonded with prestressed CFRP plates [J]. Journal of Building Structures, 2011, 32(4): 95 − 100. (in Chinese)




 下载:
下载: