THEORETICAL STUDY ON THE LIMIT ROLLABLE THICKNESS OF THIN STRIP BASED UPON ROLLING FORCE
-
摘要:
极限可轧厚度是薄带材轧制过程中判断轧件是否可以继续减薄的重要理论判据，然而现有的理论公式很少考虑轧件可轧性的工艺相关性，该文通过有限元手段研究了薄带轧制变形区特征随轧制工艺的变化规律，并基于赫兹弹性理论和一点弹塑性应力状态开展了以轧制力作为判别依据的极限可轧厚度理论研究。结果表明轧件可轧性与轧制工艺密切相关，临近极限可轧厚度时变形区内以弹性变形为主，所对应的接触压力分布符合赫兹弹性理论。通过比较极值点的等效应力与轧件屈服强度的大小关系可以准确判断轧件的弹塑性状态，而采用极限单位宽度轧制力可较好地预测给定工艺下轧件的可轧性，并反推给定轧制力下的极限可轧厚度。
Abstract:The limit rollable thickness is an important theoretical criterion for judging whether the rolled parts can continue to be thinned further during the thin strip rolling process, but the existing theoretical models rarely consider the effect of rolling process on the rollability of rolled parts. As a result, the variation law of the deformation zone features of thin strip rolling with the rolling process is studied by finite element simulation in this study. Furthermore, the Hertz elastic theory and the elastic-plastic stress state of a point are used to conduct theoretical study on the limit rollable thickness based on the rolling force. The results demonstrate that the rolled part rollability is closely related to the rolling process, that as the limit rollable thickness approaches, elastic deformation occurs mostly in the deformation zone, and that the corresponding contact pressure distribution conforms to the Hertz elastic theory. By comparing the relationship between the equivalent stress of the extreme point and the yield strength, the elastoplastic state of the rolled part can be accurately assessed, and the rolling force per unit width can be used to better predict the rollability of the rolled part under a given process, and the limit rollable thickness under the given rolling force can be reversed.
-
随着产品加工制造越来越趋向小型轻量化和功能精细化方向发展，其对技术密集型高品质金属薄带材的需求也大幅提升[1 − 2]。薄带材轧制问题的理论研究主要针对：1)平面应变假设下的变形区接触理论和可轧厚度等问题[3 − 5]；2)金属空间流动时的板形和板凸度等问题[6 − 8]。其中最小可轧厚度理论的提出与发展旨在定量描述薄带材类产品越薄越难轧的现象，其认为轧件厚度减小到某一理论值时继续增加轧制力也不能使其产生进一步的塑性压缩，该理论也逐渐成为轧机装备设计和轧制工艺制定的重要理论依据[9]。
最小可轧厚度理论是伴随着对变形区接触特征认识的不断深入而发展的，其中应用最广且最具代表性的为Stone最小可轧厚度公式[10]，其由轧辊直径和弹性模量、轧件屈服强度、摩擦系数和张应力组成的表达式实现定量计算，后续理论也均保持了相似的表达形式。然而实验结果表明厚度小于Stone理论值时仍可实现百分之几十的压下量[11 − 14]，误差来源于Stone理论所采用的Hitchcock弧长公式，其假设轧辊弹性压扁后仍始终保持圆弧形轮廓[15 − 16]，显然此假设并不适用于变形区形状系数远大于1的薄带材轧制。除此之外，Stone理论还假设整个接触界面均存在相对滑移，且认为轧件状态会由塑性变形瞬时转变为弹性变形的假设也不符合实际。为此FORD等[17 − 18]则以全弹性带假设为基础提出了新的最小可轧厚度公式，不足之处是该理论同样认为轧辊弹性压扁后轮廓呈圆弧形，且轧件变形首先发生于变形区中心截面处的假设也并不合理。JOHNSON和BENTALL等[19 − 20]则在Ford-Alexander全弹性带基础上考虑了变形区摩擦条件的变化，认为薄带轧制塑性压下分布于入口和出口处，而中心区不产生塑性变形。随后FLECK等[21 − 22]在Johnson的基础上修正了赫兹接触模型，摒弃了轧辊始终保持圆弧形的假设，将变形区划分为入口弹性区、入口塑性区、中性区、出口塑性区和出口弹性区，而中性区内无相对滑移。许多学者通过实验或有限元等手段验证了Felck模型的正确性，并对其解析过程进行了适当简化[23 − 27]。刘晓等 [28]和XIAO等[28 − 29]则在Fleck模型的基础上将入口塑性区宽度为零作为轧件弹塑性状态转变的临界条件，提出了新的最小可轧厚度公式，所得最小值仅为Stone理论值的22%，并将Stone最小可轧厚度作为衡量中性区出现的临界值。综上所述，可轧厚度理论研究的关键在于对变形区内轧件弹塑性状态的合理认识及对转变临界点的准确判别。
然而现有最小可轧厚度公式的共同点亦是其不足之处为均未考虑工艺相关性，从受力角度分析可知当所提供的轧制力满足临界点所需时轧件便可继续产生塑性压下，而轧制力大小会受压下率、摩擦系数和轧机性能等因素影响。故若能从轧制力角度寻找弹塑性转变临界点，则可更加准确地判断轧件在给定工况下的可轧性。为此本文采用数值模拟和变形区理论推导相结合的手段，从轧制力角度探究与工艺相关的且更准确的极限可轧厚度预测方法，研究结果可为后续进一步拓展至多辊系统和复杂轧制工艺下轧件可轧性的判别奠定理论基础。
1 轧制过程有限元仿真
1.1 有限元模型建立
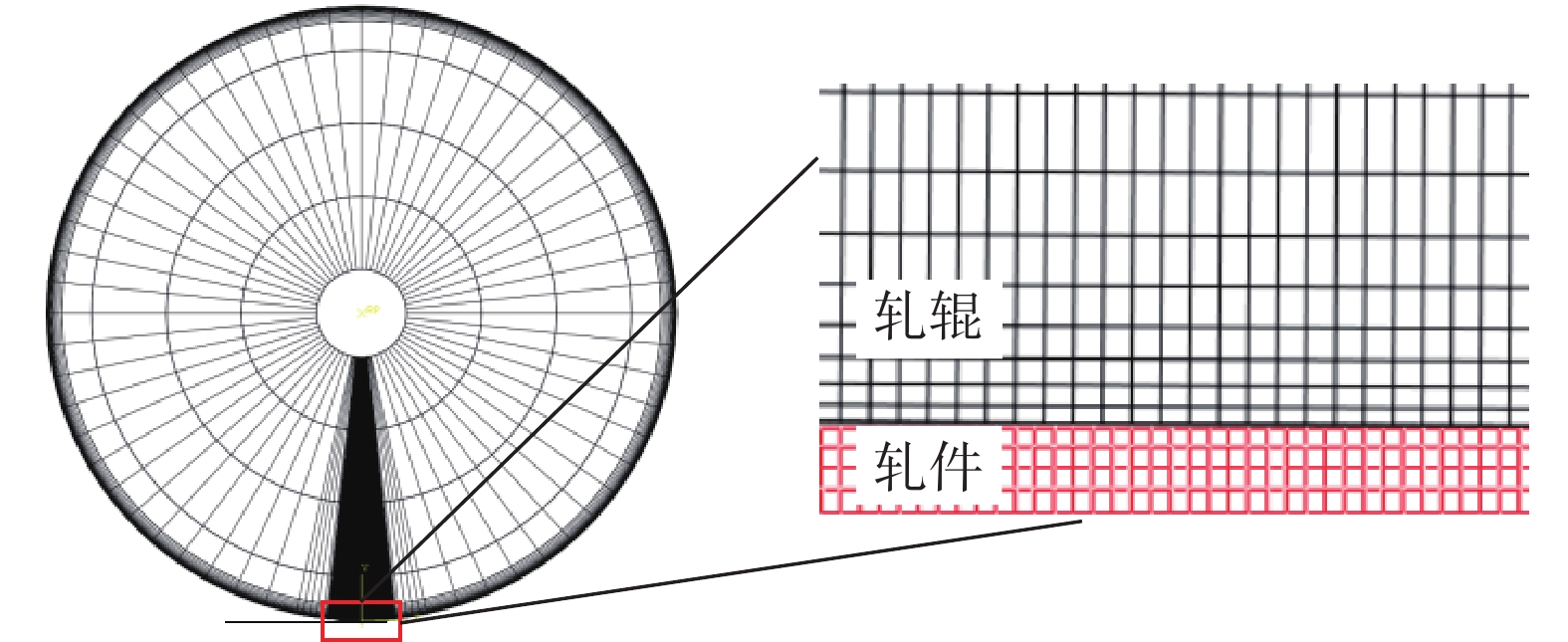
平辊轧制变形区形状系数大于3.0时，可将轧制过程简化为二维平面应变问题进行求解。本文侧重于从理论角度分析薄带轧制变形特征，故利用Abaqus软件建立了弹塑性二辊轧制模型，如图1所示。由于轧制模型关于中间水平面对称，故只选择了上工作辊和薄带上半部分作为计算对象。薄带厚度方向划分四层网格，网格类型为CPE4R四结点双线性平面应变四边形单元；对轧辊表面网格单元进行了局部细化分，与薄带网格单元尺寸比例保持在1.0~1.5。
轧辊和薄带接触界面采用库伦摩擦，由于张应力σp并不会影响分析流程，为简化暂设为0。薄带和轧辊分别设置为弹塑性体和弹性体，轧辊直径D为210 mm，弹性模量ER为236 GPa，轧辊转速为0.08 rad/s；薄带初始屈服强度σs为280 MPa，泊松比ν均为0.3。整个轧制过程可划分为压下、初轧和稳定轧制三个阶段，选择稳定轧制阶段轧件表面网格结点提取接触界面的应力应变等输出信息。
为探究薄带轧制变形区特征与轧件可轧性随轧制工艺的变化规律，引入了Stone最小可轧厚度公式[10]和XIAO最小可轧厚度公式[28]进行对比分析：
hmin (1) h_{\min }^{\mathrm{X}} = \frac{{0.78fD( {1.155{\sigma _{\mathrm{s}}} - {\sigma _{\mathrm{p}}}} )}}{{{E_{\mathrm{R}}}}} (2) 将上述参数代入式(1)和式(2)可得不同摩擦系数下的两种最小可轧厚度值，如表1所示。在表1所得最小可轧厚度附近选取薄带厚度规格h0为0.3 mm、0.2 mm、0.1 mm、0.075 mm、0.05 mm、0.03 mm、0.02 mm，预设压下率y为20%、40%、60%、80%、100%。采用薄带厚度h0-预设压下率y-摩擦系数f对轧制工艺进行命名。
表 1 不同摩擦系数时的最小可轧厚度Table 1. Minimum rollable thickness at different friction coefficients摩擦系数f STONE理论值/mm XIAO理论值/mm 0.050 0.052 0.011 0.100 0.103 0.022 0.200 0.206 0.045 0.300 0.309 0.067 1.2 模拟结果分析
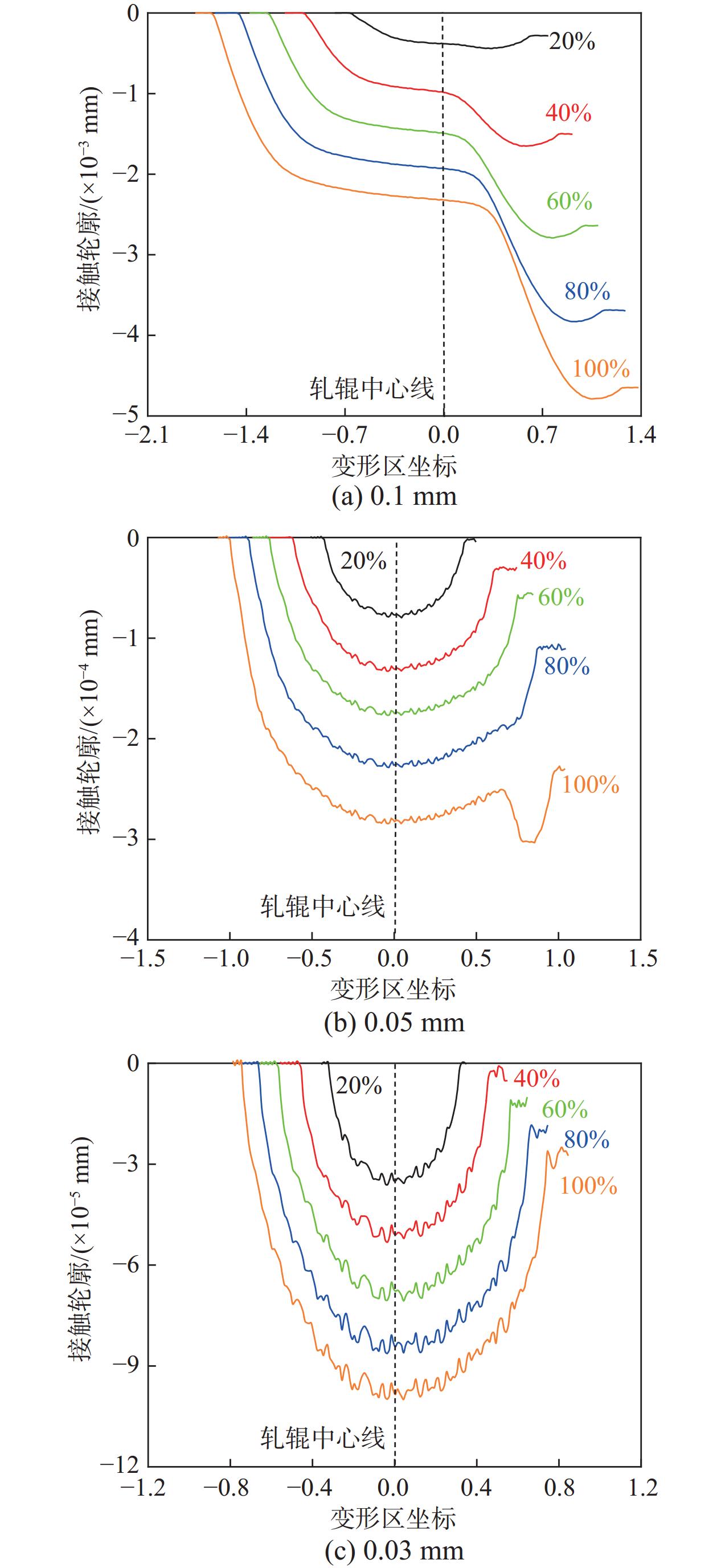
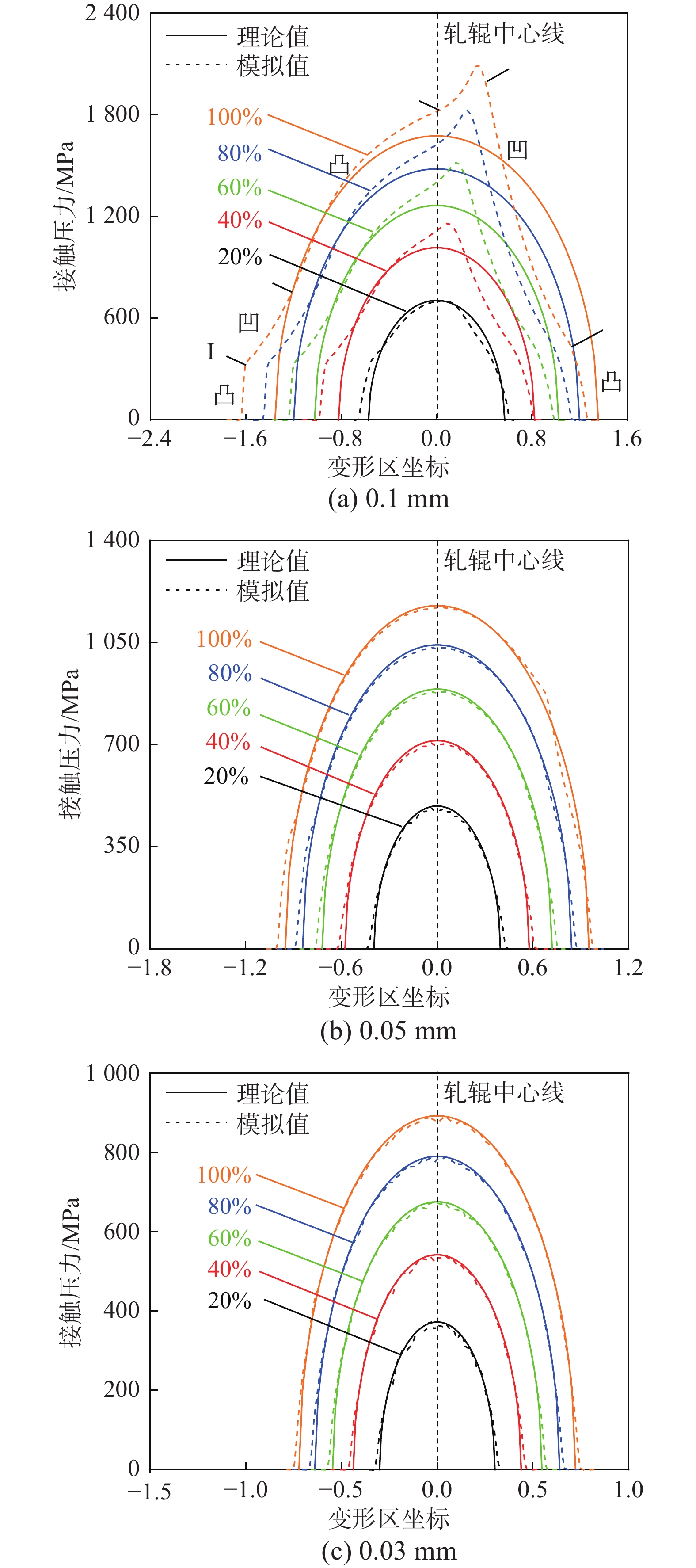
图2和图3分别为变形区接触轮廓和接触压力(虚线为模拟值，实线为赫兹理论值)随薄带厚度和预设压下率的变化曲线(f = 0.1)，图中仅显示了部分代表性工艺。依据接触轮廓分段变形特征和接触压力外凸内凹特点，以0.1 mm薄带为例可将变形区划分为入口弹性区(凸)、入口塑性区(凹)、中性区(凸)、出口塑性区(凹)和出口弹性区(凸)。
当轧辊提供的接触压力无法满足轧件进一步塑性变形所需时便会产生弹性压扁，由图2(a)可知当弹性压扁到一定程度时中性区出现并不断变宽，变形区轮廓也由圆弧形逐渐转变为非圆弧形；轧件塑性压下主要集中于入口和出口塑性区，中性区内基本呈弹性变形。与图2(b)和图2(c)对比可发现变形区接触弧长和塑性区宽度随着薄带厚度的减小而不断变小，其中出口塑性区要先于入口塑性区变窄，如0.05 mm-80%时出口塑性区基本消失；中性区宽度所占比例不断增加，实际压下量快速减小，量级由0.1 mm时的10−3 mm减小至0.03 mm时的10−5 mm。显然此时整个变形区内只存在极小的弹性变形，故变形区轮廓可近似视为直线形。
![]()
图 2 不同厚度薄带时的变形区接触轮廓Figure 2. Deformation zone contact profile at different strip thicknesses由赫兹理论可知两弹性物体之间接触压力呈半椭圆形对称分布，故可通过赫兹理论值与实际接触压力的吻合度来判断变形区内各区的弹塑性状态。由图3(a)可知赫兹半椭圆形轨迹与实际接触压力曲线吻合度随预设压下率的增加而变差，如0.1 mm-20%的吻合度最高，其它预设压下率时仅在中性区段吻合较好，归因于低压下率时和中性区内均以弹性变形为主。对比图3(b)和图3(c)可发现吻合度随薄带厚度的减小而不断增加，0.05 mm时除入口塑性区和出口塑性区外基本吻合，而0.03 mm时整个变形区接触压力曲线与赫兹理论结果基本重合。
![]()
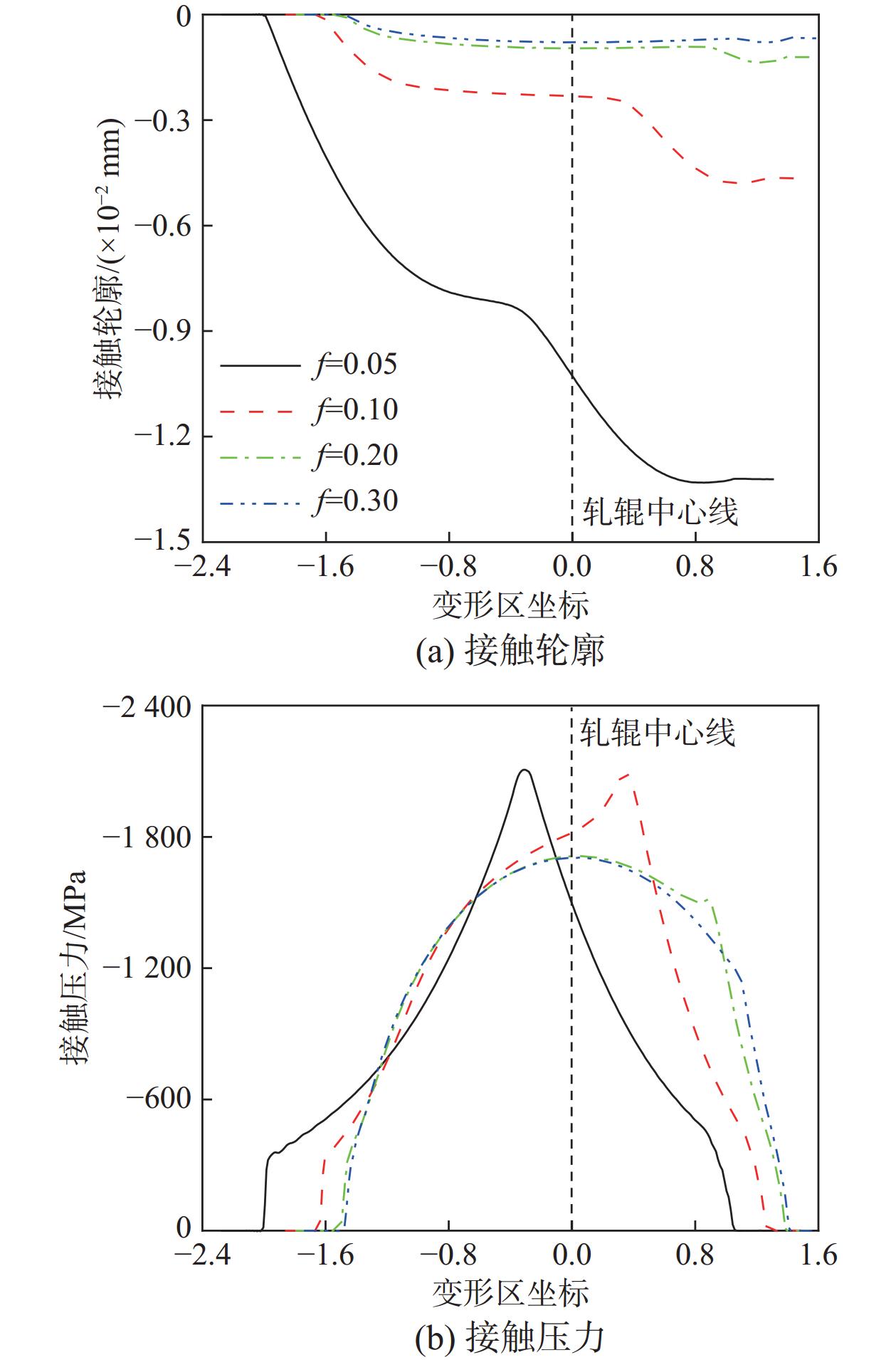
图 3 不同厚度薄带时的变形区接触压力与赫兹理论值对比图Figure 3. Comparison of simulation value and hertz contact theoretical value of contact pressure under differentstrip thicknesses图4为0.1 mm-100%工艺下变形区接触轮廓和接触压力随摩擦系数的变化规律。由图4(a)可知随着摩擦系数的增大，中性区出现得更早且宽度占比更大，而入口和出口塑性区逐渐变窄；实际压下量大幅减小，如由f = 0.05时−1.3×10−2 mm减小到f = 0.1时−0.45×10−2 mm。由图4(b)同样可发现随着中性区宽度的增加，接触压力曲线峰值逐渐消失，并越来越趋近于赫兹半椭圆形分布。上述结果表明给定工艺下，变形区以弹性变形为主时的接触压力分布近似符合赫兹弹性理论。
![]()
图 4 0.1mm-100%工艺下的变形区接触轮廓和接触压力Figure 4. Deformation zone contact profile and contact pressure under 0.1mm-100% process表2为不同薄带厚度时预设压下率与实际压下率的对应关系(f = 0.1)。由表2可知轧辊弹性压缩乃至中性区的出现导致实际压下率均远小于预设压下率，其中0.1 mm-100%-0.1、0.075 mm-100%-0.1和0.05 mm-100%-0.1时分别仍可以产生约10%、5%和1%的道次压下率，显然其远小于Stone最小可轧厚度0.103 mm。道次压下率随薄带厚度的减小而快速减小，0.03 mm~0.02 mm-20%~60%-0.1时的道次压下率均接近或已经为0，即便0.02 mm-100%-0.1时道次压下率也仅为0.08%，接近Xiao理论值0.022 mm。
表3为不同摩擦系数时预设压下率与实际压下率的对应关系。由表3可知相同预设压下率时实际压下率随摩擦系数的增加而快速减小，如由0.1 mm-60%-0.05时16.4%减小至0.1 mm-60%-0.3时0.53%。0.2 mm~0.1 mm-100%-0.3时仍可实现10.7%和1.3%的实际压下率，即便0.05 mm-100%-0.3时仍可产生约0.1%的实际压下率。显然其可轧厚度要远小于此摩擦系数下Stone最小可轧厚度0.309 mm，并且对比可发现Xiao理论值0.067 mm要比Stone理论值更加接近真实值。简单分析可知当轧件厚度达到最小可轧厚度时，轧辊与轧件均只能产生弹性变形，此时整个变形区接触界面上无相对位移，这也是导致建立在全滑移摩擦条件和圆弧形轮廓假设下的Stone理论值大幅偏离实际的原因。
表 2 不同厚度薄带时预设压下率与实际压下率的对应关系Table 2. The correspondence between the preset reduction rate and the actual reduction rate at different strip thicknesses预设压下率
y/(%)薄带厚度h/mm 0.30 0.20 0.10 0.075 0.05 0.03 0.02 20 7.96 5.10 0.56 0.10 0.00 0.00 0.00 40 17.10 11.60 3.00 0.88 0.15 0.01 0.00 60 24.50 16.10 5.30 2.20 0.22 0.04 0.00 80 29.70 20.00 7.40 3.40 0.43 0.12 0.05 100 34.70 23.30 9.30 4.60 0.90 0.17 0.08 表 3 不同摩擦系数时预设压下率与实际压下率的对应关系Table 3. The correspondence between the preset reduction rate and the actual reduction rate at different friction coefficients薄带厚度
h/mm预设压下率
y/(%)摩擦系数f 0.05 0.10 0.20 0.30 0.20 30 14.10 9.20 3.50 2.00 60 32.90 16.50 6.60 4.50 100 52.20 25.00 12.30 10.70 0.10 30 6.40 1.78 0.25 0.22 60 16.40 5.30 1.05 0.53 100 26.30 9.30 2.40 1.30 0.05 30 0.30 0.12 0.05 0.04 60 3.10 0.22 0.10 0.08 100 6.89 0.90 0.31 0.09 然而需要注意的是，虽然Xiao最小可轧厚度已经很接近真实值，但由表2和表3结果可发现0.02 mm-100%-0.1、0.05 mm-100%-0.3时均仍可产生约0.1%实际压下率，即通过多道次累积轧制仍可得到更薄规格带材。除此之外，若采用轧后厚度或道次压下率来衡量轧件可轧性，则0.05 mm-20%-0.1、0.03 mm-20%~40%-0.1、0.02 mm-20%~60%-0.1和0.05 mm-30%-0.3时的实际压下率也基本均为0。上述工艺下轧件已无法产生塑性变形，但显然其并未达到Xiao最小可轧厚度。而实际轧制过程中轧制系统所能提供的轧制力还需考虑轧机性能和轧制工艺的影响，换言之，真实的可轧厚度是与轧制工艺和轧机性能相关的，而绝对的最小可轧厚度并不存在。因此若能从轧制力角度对轧件弹塑性转变状态进行判别，则可以更准确地判断给定工艺下轧件的可轧性，并反推此工艺下的最小可轧厚度。
2 基于轧制力判定的极限可轧厚度
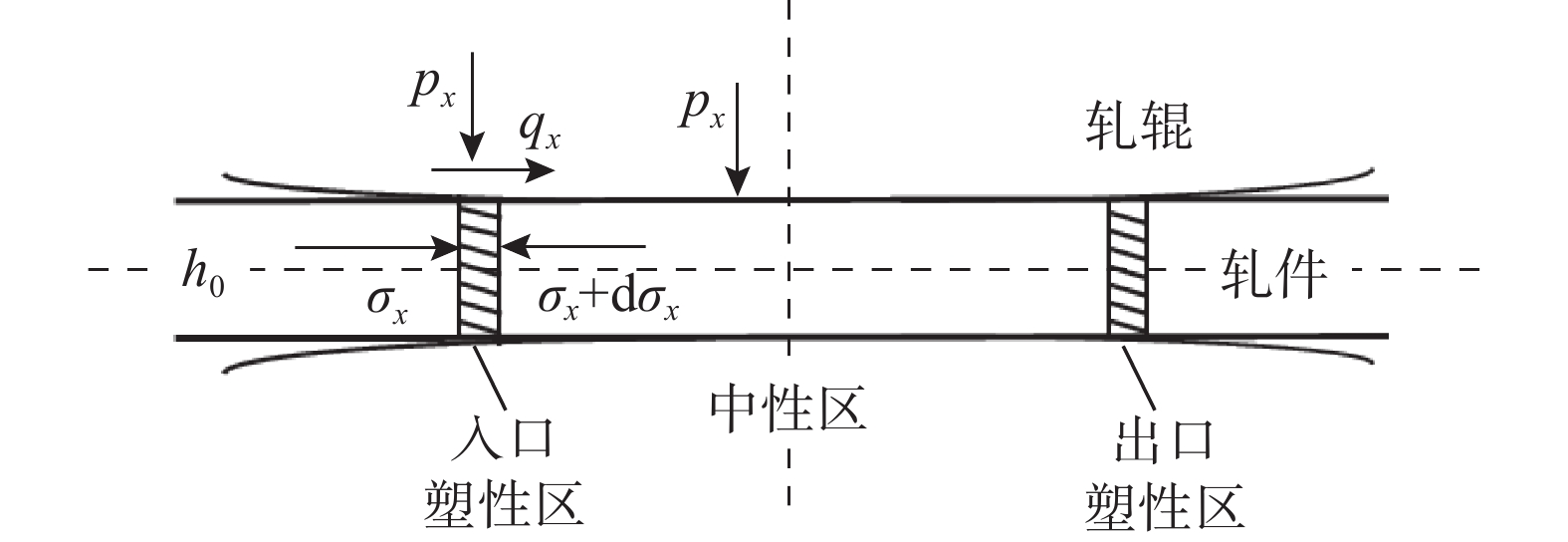
为便于与式(1)和式(2)两种理论公式进行区分，本文将与轧制工艺相关的最小可轧厚度定义为极限可轧厚度。已知当接近极限可轧厚度时变形区以弹性变形为主，极小的塑性变形集中于塑性区，此时变形区轮廓近似直线，接触压力分布符合赫兹弹性理论。因此极限可轧厚度分析时可将轧制过程简化为两个平板之间的压缩，如图5所示。
![]()
图 5 变形区微元体受力示意图Figure 5. Schematic diagram of the force of the microelement in the deformation zone根据塑性区内单元体水平方向合力为零，可得平衡微分方程为：
\frac{{{\mathrm{d}}{\sigma _x}}}{{{\mathrm{d}}x}} = \frac{{q\left( x \right)}}{{{h_0}}} (3) 塑性区内轧辊与轧件之间满足库伦摩擦条件：
{q_x} = f{p_x} (4) 式中：px为轧辊所提供接触压力；qx为摩擦力；σx为纵向应力。塑性变形依托于Tresca屈服判据：
\left| {{\sigma _1} - {\sigma _3}} \right| = {\sigma _{{\mathrm{eq}}}} {\geqslant} {\sigma _{\mathrm{s}}} (5) 式中，σeq和σs分别为等效应力和轧件屈服强度。平面应变状态时变形区内应力分量近似满足：
{\sigma _x} = {\sigma _3} \;,\qquad {p_x} = {\sigma _1} (6) 则平面应变情况下考虑中间主应力影响时，屈服判据可表示为：
{p_x} - {\sigma _x} = \frac{{2\sqrt 3 }}{3}{\sigma _{\mathrm{s}}} \approx 1.155{\sigma _{\mathrm{s}}} (7) 将轧件表面的压力分布近似匹配到轧辊表面的赫兹压力：
{\sigma _{\text{1}}} = p\left( x \right) = \frac{{2{p_{\mathrm{w}}}}}{{\pi a}}{( {1 - {X^2}} )^{1/2}} (8) 式中，X=x/a，a为半接触弧长，x轧件所处变形区位置，因此X∈[−1, 1]。由赫兹理论可得两圆柱体弹性压缩时的等效半接触弧长为：
a = {\left( {\frac{{4{p_{\mathrm{w}}}R}}{{\pi {E^ * }}}} \right)^{1/2}} (9) 式中：E*为平面应变模量，E*=(1−ν2)/ER；pw为单位宽度轧制力，表示单位宽度的轧件变形时所需轧制力，由接触压力沿变形区弧长积分获得。
利用换元法对式(3)中的dσx进行积分，以主应力表示σX的计算过程为：
\int_{ - a}^a {q\left( x \right)} {\mathrm{d}}x = f\int_{ - a}^a {p\left( x \right)} {\mathrm{d}}x = fa\int_{ - 1}^1 {p\left( X \right)} {\mathrm{d}}X (10) \int_{ - 1}^1 {\sqrt {1 - {X^2}} } {\mathrm{d}}X = \int_{ - \pi /2}^{\pi /2} {{{\cos }^2}t} {\mathrm{d}}t (11) \begin{aligned} & {\sigma _{\text{3}}} = {\sigma _{{x}}} = \frac{{af}}{{{h_0}}}\int_{ - 1}^1 {p\left( X \right){\mathrm{d}}X} =\\&\qquad \frac{{2{p_{\mathrm{w}}}}}{{\pi a}}\frac{{fa}}{{{h_0}}}\left[ {X{{( {1 - {X^2}} )}^{1/2}} + {{\sin }^{ - 1}}X - \frac{\pi }{2}} \right] \end{aligned} (12) 将σ1和σ3代入式(5)中可得：
\begin{split} & {\sigma _{{X_{\mathit{C}}}}} = \frac{{2p{}_{\mathrm{w}}}}{{\pi a}}\Bigg[ {( {1 - {X^2}} )^{1/2}} - \\&\qquad \frac{{fa}}{{2{h_0}}}\left\{ {\frac{\pi }{2} - X{{( {1 - {X^2}} )}^{1/2}} - {{\sin }^{ - 1}}X} \right\} \Bigg] \end{split} (13) 通过对X微分求导，一阶导数为零的点即为等效应力极值点XC：
{X_{\mathit{C}}} = - \frac{{{h_0}}}{{2fa}} + {\left( {{{\left( {\frac{{{h_0}}}{{2fa}}} \right)}^2} + 1} \right)^{1/2}} (14) 根据变形区各区轧件变形特点可知入口侧等效应力极值点XC即为入口塑性区和中性区的临界点，故可利用XC处等效应力值与轧件屈服强度进行比较，以判断轧件是否可以产生塑性变形：
\left\{ \begin{aligned} & {\sigma }_{{X}_{{\rm{C}}}}\geqslant 1.155{\sigma }_{{\mathrm{s}}},\;\; 有塑性区\text{，}可轧\\& {\sigma }_{{X}_{{\rm{C}}}} \lt 1.155{\sigma }_{{\mathrm{s}}},\;\; 无塑性区\text{，}不可轧 \end{aligned}\right. (15) 由式(9)和式(14)可知给定轧制模型参数和轧制工艺后，pw、a和XC之间是相互关联且固定的。联立式(13)和式(15)可得：
\begin{split} & \delta \left( X \right) = \frac{{2{p_{\mathrm{w}}}}}{{\pi a}}\Bigg[ {( {1 - {X_{\mathit{{C}}}^2}} )^{1/2}} - \\&\quad \frac{{fa}}{{2{h_0}}}\Bigg\{ \frac{\pi }{2} - {X_{\mathit{C}}}{( {1 - {X_{\mathit{{C}}}^2}} )^{1/2}} - {\sin ^{ - 1}}{X_{\mathit{C}}} \Bigg\} \Bigg] - 1.155{\sigma _{\mathrm{s}}} \end{split} (16) 式中，δ(X)为等效应力值与轧件屈服强度的差值。考虑到式(16)中薄带厚度h0的解析解很难获得，故可通过作图法进行计算与屈服判别，并反求对应工艺下的极限可轧厚度。
3 结果与讨论
3.1 等效应力极值点XC
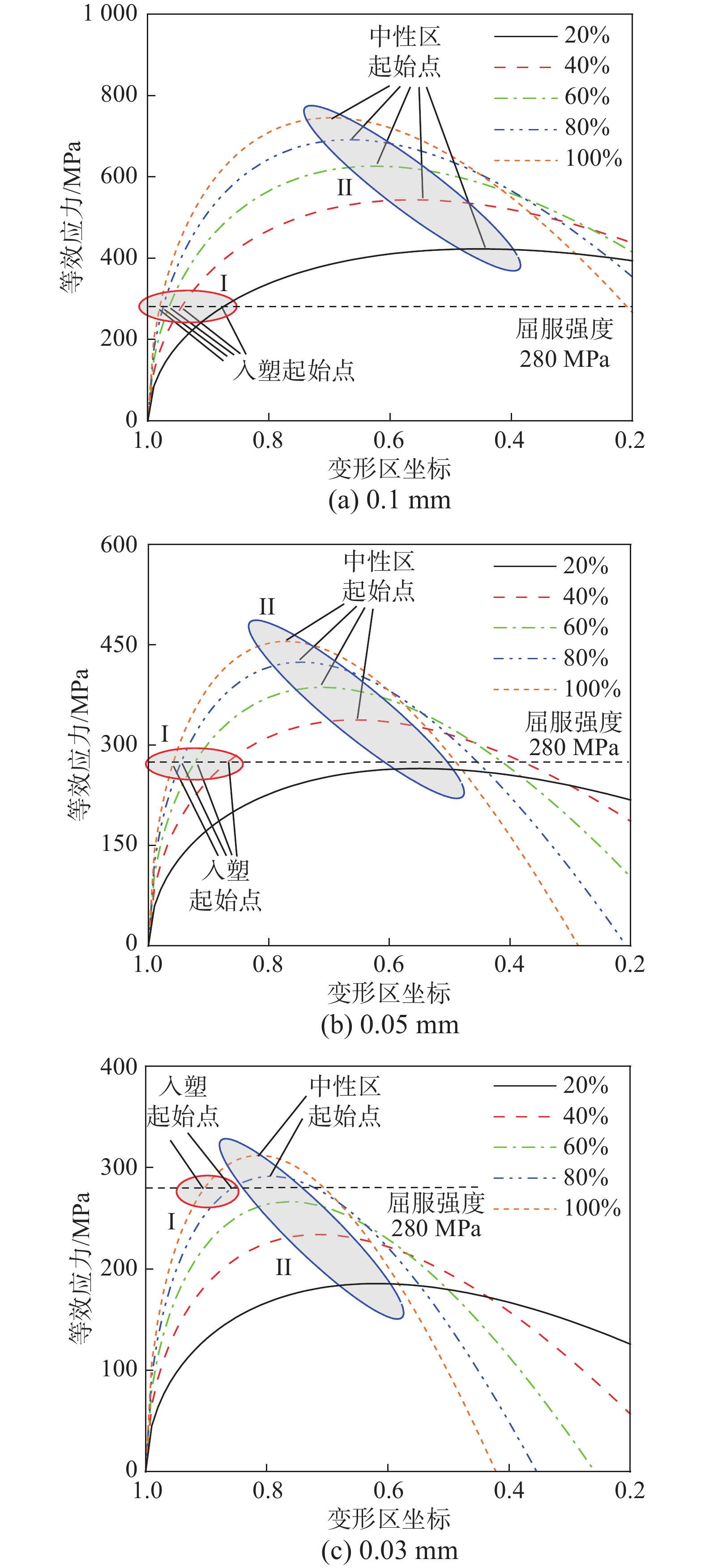
由式(14)可得不同轧制工艺下入口侧的等效应力极值点XC，图6为不同轧制工艺下的变形区等效应力轨迹(f = 0.1)，此图仅显示了部分工艺。图6中红色圆框I处表示等效应力曲线与280 MPa屈服强度虚线相交点，对应入口弹性区与入口塑性区的分界点XB。蓝色圆框II处表示等效应力极值点，对应入口塑性区与中性区的分界点XC。由图可知0.1 mm时不同预设压下率时均存在塑性区，0.05 mm-20%时无入口塑性区，而0.03 mm预设压下率小于60%时无入口塑性区，与表2中所得结果相符。
![]()
图 6 不同预设压下率时的变形区等效应力轨迹Figure 6. Equivalent stress trajectory in deformation zone at different preset reduction rate图6中所得坐标值为归一化结果，对其进行反归一化处理可得图7。图7为入口塑性区起始点坐标xB与中性区起始点坐标xC的理论值与模拟值。由图可知入口塑性区起始点和中性区起始点坐标的预测精度随着薄带厚度的减小而不断升高，0.05 mm厚及以下厚度时理论值与模拟值基本吻合。
![]()
图 7 入口塑性区临界点的理论值与模拟值Figure 7. Theoretical and simulated values of critical points of inlet plastic zone3.2 极限单位宽度轧制力p_ {\mathrm{w}}^{{\mathrm{limit}}}
图8为应力差值δ(X)随单位宽度轧制力的变化曲线，其中δ(X) = 0表示入口塑性区恰好不存在，δ(X)与该零线交点代表发生塑性压下所需的最小单位宽度轧制力，定义为极限单位宽度轧制力p_ {\mathrm{w}}^{{\mathrm{limit}}} 。当给定工艺下的单位宽度轧制力pw大于轧件变形所需极限单位宽度轧制力p_ {\mathrm{w}}^{{\mathrm{limit}}} 时便能够产生塑性变形，相反则意味着此工艺下轧件不可轧。
![]()
图 8 不同薄带厚度时应力差值随单位宽度轧制力的变化规律Figure 8. Change law of stress difference with unit width rolling force at different strip thicknesses图8中数据散点为本文所选轧制工艺，其所对应的轧制工艺、单位宽度轧制力和极限单位宽度轧制力见表4。由图8可知0.1 mm和0.075 mm时所有工艺下均可产生塑性压下，0.05 mm时在P24、P30、P33、P34和P35，0.03 mm时在P36、P37和P38时均无法产生塑性压下。由表4可发现此时的轧辊所提供的单位宽度轧制力均未达到极限值，而结合表2和表3可发现其实际压下率均小于0.1%，也进一步证明了采用单位宽度轧制力预测轧件可轧性的可行性和准确性。
表 4 图8中数据点所对应的轧制工艺和单位宽度轧制力Table 4. The rolling process and unit width rolling force corresponding to the data points in Fig. 8数据点 薄带厚度h/mm-摩擦系数f-
预设压下率y/(%)单位宽度
轧制力pw /Np_ {\mathrm{w} }^{ {\mathrm{limit} } } 数据点 薄带厚度h/mm-摩擦系数f-
预设压下率 y/(%)单位宽度
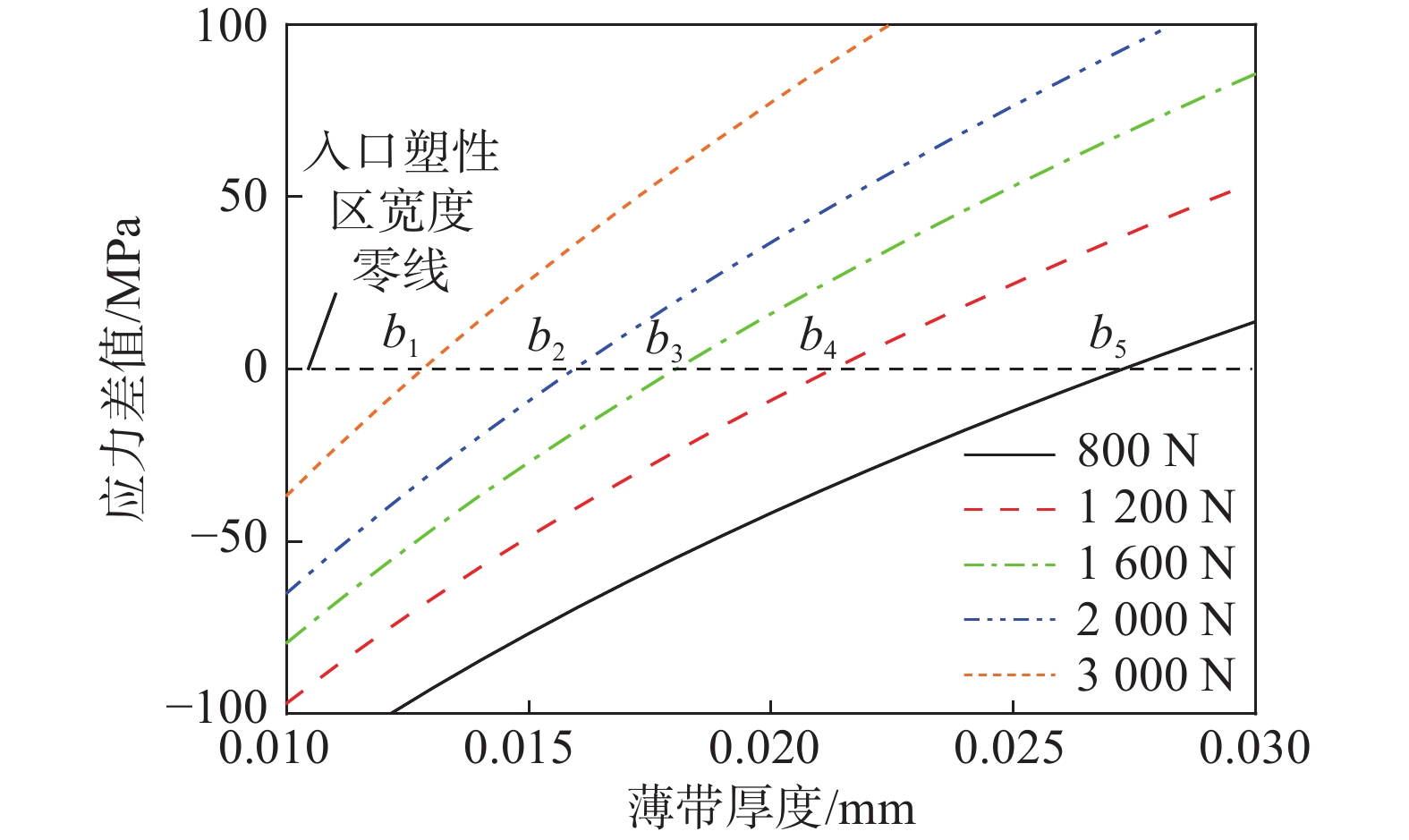
轧制力pw /Np_ {\mathrm{w} }^{ {\mathrm{limit} }} P1 0.10-0.05-30 833.7 165.8 P21 0.05-0.05-30 470.9 212.2 P2 0.10-0.05-60 1680.6 P22 0.05-0.05-60 977.9 P3 0.10-0.05-100 3051.0 P23 0.05-0.05-100 1693.2 P4 0.10-0.10-20 632.5 212.2 P24 0.05-0.10-20 305.0 359.7 P5 0.10-0.10-30 967.5 P25 0.05-0.10-30 473.7 P6 0.10-0.10-40 1313.7 P26 0.05-0.10-40 647.9 P7 0.10-0.10-60 2036.2 P27 0.05-0.10-60 1008.4 P8 0.10-0.10-80 2790.9 P28 0.05-0.10-80 1380.3 P9 0.10-0.10-100 3572.1 P29 0.05-0.10-100 1760.6 P10 0.10-0.20-30 999.7 360.0 P30 0.05-0.20-30 474.1 917.5 P11 0.10-0.20-60 2133.4 P31 0.05-0.20-60 1009.4 P12 0.10-0.20-100 3737.5 P32 0.05-0.20-100 1766.2 P13 0.10-0.30-30 1000.6 593.5 P33 0.05-0.30-30 474.3 1841.8 P14 0.10-0.30-60 2141.8 P34 0.05-0.30-60 1009.6 P15 0.10-0.30-100 3759.1 P35 0.05-0.30-100 1766.5 P16 0.075-0.10-20 470.7 252.5 P36 0.03-0.10-20 176.2 691.1 P17 0.075-0.10-40 994.9 P37 0.03-0.10-40 373.5 P18 0.075-0.10-60 1540.1 P38 0.03-0.10-60 580.1 P19 0.075-0.10-80 2105.7 P39 0.03-0.10-80 793.6 P20 0.075-0.10-100 2688.2 P40 0.03-0.10-100 1012.3 同理当给定某一工艺下的单位宽度轧制力或给定轧机所能提供的单位宽度轧制力上限时，也可根据式(16)反求出对应工况下的极限可轧厚度。图9为相同单位宽度轧制力时δ(X)随薄带厚度的变化规律，由图可知极限可轧厚度随着单位宽度轧制力的升高而不断减小，δ(X) = 0表示此厚度时轧件刚好可以产生变形，小于此厚度时不可轧。b1~b5即为对应单位宽度轧制力时的极限可轧厚度，分别为b1 = 0.013 mm (3000 N)、b2 = 0.016 mm (2000 N)、b3 = 0.018 mm (1600 N)、b4 = 0.022 mm (1200 N)和b5 = 0.028 mm (800 N)。
4 结论
本文探究了薄带材轧制变形区特征随轧制工艺的变化规律，并基于赫兹弹性理论和一点弹塑性应力状态推导了采用轧制力判定的极限可轧厚度，所得结论如下：
(1) 薄带材轧制时存在显著的轧辊弹性压扁现象，而中性区的出现导致轧辊轮廓由圆弧形转变为非圆弧形；塑性变形集中于入口和出口塑性区，而中性区内为弹性变形，并且中性区的出现和变宽是导致实际压下率快速降低的主要原因。
(2) 轧件极限可轧厚度是与轧制工艺密切相关的，而绝对的最小可轧厚度并不存在。当接近极限可轧厚度时整个变形区内以弹性变形为主，此时的变形区轮廓可近似视为直线形，所对应的接触压力符合赫兹弹性理论的半椭圆形分布。
(3) 等效应力极值点对应入口塑性区和中性区临界点，通过比较极值点等效应力与轧件屈服强度或单位宽度轧制力与极限单位宽度轧制力的大小可更准确地判断给定轧制工艺下轧件可轧性，并反推给定轧制力时的理论极限可轧厚度。
-
![]()
图 2 不同厚度薄带时的变形区接触轮廓
Figure 2. Deformation zone contact profile at different strip thicknesses
![]()
图 3 不同厚度薄带时的变形区接触压力与赫兹理论值对比图
Figure 3. Comparison of simulation value and hertz contact theoretical value of contact pressure under differentstrip thicknesses
![]()
图 4 0.1mm-100%工艺下的变形区接触轮廓和接触压力
Figure 4. Deformation zone contact profile and contact pressure under 0.1mm-100% process
![]()
图 5 变形区微元体受力示意图
Figure 5. Schematic diagram of the force of the microelement in the deformation zone
![]()
图 6 不同预设压下率时的变形区等效应力轨迹
Figure 6. Equivalent stress trajectory in deformation zone at different preset reduction rate
![]()
图 7 入口塑性区临界点的理论值与模拟值
Figure 7. Theoretical and simulated values of critical points of inlet plastic zone
![]()
图 8 不同薄带厚度时应力差值随单位宽度轧制力的变化规律
Figure 8. Change law of stress difference with unit width rolling force at different strip thicknesses
表 1 不同摩擦系数时的最小可轧厚度
Table 1 Minimum rollable thickness at different friction coefficients
摩擦系数f STONE理论值/mm XIAO理论值/mm 0.050 0.052 0.011 0.100 0.103 0.022 0.200 0.206 0.045 0.300 0.309 0.067 
下载: 导出CSV
表 2 不同厚度薄带时预设压下率与实际压下率的对应关系
Table 2 The correspondence between the preset reduction rate and the actual reduction rate at different strip thicknesses
预设压下率
y/(%)薄带厚度h/mm 0.30 0.20 0.10 0.075 0.05 0.03 0.02 20 7.96 5.10 0.56 0.10 0.00 0.00 0.00 40 17.10 11.60 3.00 0.88 0.15 0.01 0.00 60 24.50 16.10 5.30 2.20 0.22 0.04 0.00 80 29.70 20.00 7.40 3.40 0.43 0.12 0.05 100 34.70 23.30 9.30 4.60 0.90 0.17 0.08
下载: 导出CSV
表 3 不同摩擦系数时预设压下率与实际压下率的对应关系
Table 3 The correspondence between the preset reduction rate and the actual reduction rate at different friction coefficients
薄带厚度
h/mm预设压下率
y/(%)摩擦系数f 0.05 0.10 0.20 0.30 0.20 30 14.10 9.20 3.50 2.00 60 32.90 16.50 6.60 4.50 100 52.20 25.00 12.30 10.70 0.10 30 6.40 1.78 0.25 0.22 60 16.40 5.30 1.05 0.53 100 26.30 9.30 2.40 1.30 0.05 30 0.30 0.12 0.05 0.04 60 3.10 0.22 0.10 0.08 100 6.89 0.90 0.31 0.09
下载: 导出CSV
表 4 图8中数据点所对应的轧制工艺和单位宽度轧制力
Table 4 The rolling process and unit width rolling force corresponding to the data points in Fig. 8
数据点 薄带厚度h/mm-摩擦系数f-
预设压下率y/(%)单位宽度
轧制力pw /Np_ {\mathrm{w} }^{ {\mathrm{limit} } } 数据点 薄带厚度h/mm-摩擦系数f-
预设压下率 y/(%)单位宽度
轧制力pw /Np_ {\mathrm{w} }^{ {\mathrm{limit} }} P1 0.10-0.05-30 833.7 165.8 P21 0.05-0.05-30 470.9 212.2 P2 0.10-0.05-60 1680.6 P22 0.05-0.05-60 977.9 P3 0.10-0.05-100 3051.0 P23 0.05-0.05-100 1693.2 P4 0.10-0.10-20 632.5 212.2 P24 0.05-0.10-20 305.0 359.7 P5 0.10-0.10-30 967.5 P25 0.05-0.10-30 473.7 P6 0.10-0.10-40 1313.7 P26 0.05-0.10-40 647.9 P7 0.10-0.10-60 2036.2 P27 0.05-0.10-60 1008.4 P8 0.10-0.10-80 2790.9 P28 0.05-0.10-80 1380.3 P9 0.10-0.10-100 3572.1 P29 0.05-0.10-100 1760.6 P10 0.10-0.20-30 999.7 360.0 P30 0.05-0.20-30 474.1 917.5 P11 0.10-0.20-60 2133.4 P31 0.05-0.20-60 1009.4 P12 0.10-0.20-100 3737.5 P32 0.05-0.20-100 1766.2 P13 0.10-0.30-30 1000.6 593.5 P33 0.05-0.30-30 474.3 1841.8 P14 0.10-0.30-60 2141.8 P34 0.05-0.30-60 1009.6 P15 0.10-0.30-100 3759.1 P35 0.05-0.30-100 1766.5 P16 0.075-0.10-20 470.7 252.5 P36 0.03-0.10-20 176.2 691.1 P17 0.075-0.10-40 994.9 P37 0.03-0.10-40 373.5 P18 0.075-0.10-60 1540.1 P38 0.03-0.10-60 580.1 P19 0.075-0.10-80 2105.7 P39 0.03-0.10-80 793.6 P20 0.075-0.10-100 2688.2 P40 0.03-0.10-100 1012.3
下载: 导出CSV
-
[1] MISHRA M K, DUBEY V, MISHRA P M, et al. MEMS technology: A review [J]. Journal of Engineering Research and Reports, 2019, 4(1): 1 − 24.
[2] FU M W, WANG J L, KORSUNSKY A M. A review of geometrical and microstructural size effects in micro-scale deformation processing of metallic alloy components [J]. International Journal of Machine Tools and Manufacture, 2016, 109: 94 − 125. doi: 10.1016/j.ijmachtools.2016.07.006
[3] 肖宏, 刘晓. 极薄箔带轧制的适轧厚度理论及数值模拟[J]. 钢铁, 2019, 54(6): 48 − 55. XIAO Hong, LIU Xiao. Theory and numerical simulation of gauge suitable to roll in ultra-thin strip rolling [J]. Iron and Steel, 2019, 54(6): 48 − 55. (in Chinese)
[4] LIU X, XIAO H. Theoretical and experimental study on the producible rolling thickness in ultra-thin strip rolling [J]. Journal of Materials Processing Technology, 2020, 278: 116537. doi: 10.1016/j.jmatprotec.2019.116537
[5] 吝水林, 孙建亮, 彭艳. 偏载状态下轧机轴承接触力学模型研究[J]. 工程力学, 2021, 38(1): 231 − 240. doi: 10.6052/j.issn.1000-4750.2020.03.0139 LIN Shuilin, SUN Jianliang, PENG Yan. Research on contact mechanical model of rolling mill bearing under misligned loads [J]. Engineering Mechanics, 2021, 38(1): 231 − 240. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.03.0139
[6] 王元清, 刘晓玲, 刘明, 等. 纵向变厚度(LP)钢板轧制技术和受弯构件承载性能研究[J]. 工程力学, 2019, 36(11): 1 − 12. doi: 10.6052/j.issn.1000-4750.2018.06.ST02 WANG Yuanqing, LIU Xiaoling, LIU Ming, et al. Rolling technology of longitudinally profiled steel plate (LP steel plate) and bearing capacity of LP flexural members [J]. Engineering Mechanics, 2019, 36(11): 1 − 12. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.06.ST02
[7] 张清东, 文杰. 冷轧带钢板形分段接触式检测过程的力学建模与仿真[J]. 工程力学, 2013, 30(7): 235 − 241, 254. doi: 10.6052/j.issn.1000-4750.2012.03.0201 ZHANG Qingdong, WEN Jie. Mechanics modeling and simulation of piecewise contact flatness stress measurement process in cold rolling [J]. Engineering Mechanics, 2013, 30(7): 235 − 241, 254. (in Chinese) doi: 10.6052/j.issn.1000-4750.2012.03.0201
[8] 张清东, 卢兴福, 张晓峰. 正交各向异性带钢瓢曲变形行为样条有限元研究[J]. 工程力学, 2014, 31(10): 222 − 227, 256. doi: 10.6052/j.issn.1000-4750.2013.04.0310 ZHANG Qingdong, LU Xingfu, ZHANG Xiaofeng. Buckling analysis of orthotropic steel strips by the spline finite element method [J]. Engineering Mechanics, 2014, 31(10): 222 − 227, 256. (in Chinese) doi: 10.6052/j.issn.1000-4750.2013.04.0310
[9] 肖宏, 任忠凯, 刘晓, 等. 极薄带轧制变形区轧辊压扁试验与有限元模拟[J]. 钢铁, 2017, 52(1): 38 − 42. XIAO Hong, REN Zhongkai, LIU Xiao, et al. Experiment and finite element simulation of roll flattening in deformation zone for ultra-thin strip rolling [J]. Iron and Steel, 2017, 52(1): 38 − 42. (in Chinese)
[10] STONE M D. Rolling of thin strip part II[J]. Iron and Steel Engineer, 1956, 33(12): 55 − 76.
[11] PAWELSKI O, KADING G. Causes of the limiting degree of deformation in the cold rolling of thin strip [J]. Steel Research International, 1970, 41(3): 249 − 254.
[12] 朱泉, 于九明, 齐克敏. 冷轧薄板时的延伸困难问题与适轧厚度[J]. 东北工学院学报, 1988, 57(4): 420 − 426. ZHU Quan, YU Jiuming, QI Kemin. Problem of reducibility in sheet cold-rolling and gauge suitable to roll [J]. Journal of Northeast University of Technology, 1988, 57(4): 420 − 426. (in Chinese)
[13] 吴首民. 极薄带钢轧制过程中最小可轧厚度的研究[J]. 中国冶金, 2007, 17(3): 10 − 12. WU Shoumin. Research of smallest permissive-rolling thickness during strip rolling [J]. China Metallurgy, 2007, 17(3): 10 − 12. (in Chinese)
[14] TATENO J, HIRUTA T, KATSURA S, et al. Experimental analysis of thickness reduction limits in ultra thin stainless steel foil rolling [J]. ISIJ International, 2011, 51(5): 788 − 792. doi: 10.2355/isijinternational.51.788
[15] HITCHCOCK J H. Report of ASME special research committee roll neck bearings [R]. New York: ASME Research Publictions, 1935: 33-41.
[16] 刘亚星, 顾清, 张文军, 等. 超高强钢冷轧过程轧制力计算的改进模型[J]. 钢铁, 2021, 56(10): 108 − 116. LIU Yaxing, GU Qing, ZHANG Wenjun, et al. Improved model for calculating rolling load of ultra-high strength steel in cold rolling process [J]. Iron and Steel, 2021, 56(10): 108 − 116. (in Chinese)
[17] FORD H, ELLIS F, BLAND D R. Cold rolling with strip tension [J]. Journal of the Iron and Steel Institute, 1951, 168(1): 57 − 72.
[18] FORD H, ALEXANDER J M. Rolling hard materials in thin gauges [J]. Journal of the Institute of Metals, 1960, 88(6): 193 − 197.
[19] BENTALL R H, JOHNSON K L. An elastic strip in plane rolling contact [J]. International Journal of Mechanical Sciences, 1968, 10(8): 637 − 663. doi: 10.1016/0020-7403(68)90070-2
[20] JOHNSON K L, BENTALL R H. The onset of yield in the cold rolling of thin strip [J]. Journal of the Mechanics and Physics of Solids, 1969, 17(4): 253 − 264. doi: 10.1016/0022-5096(69)90015-5
[21] FLECK N A, JOHNSON K L. Towards a new theory of cold rolling thin foil [J]. International Journal of Mechanical Sciences, 1987, 29(7): 507 − 524. doi: 10.1016/0020-7403(87)90012-9
[22] FLECK N A, JOHNSON K L, MEAR M E, et al. Cold rolling of foil [J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 1992, 206(2): 119-131.
[23] LANGLANDS T A M, MCELWAIN D L S. A modified Hertzian foil rolling model: Approximations based on perturbation methods [J]. International Journal of Mechanical Sciences, 2002, 44(8): 1715 − 1730. doi: 10.1016/S0020-7403(02)00058-9
[24] LANGLANDS T A M, MCELWAIN D L S, DOMANTI S A. An approximate method for the solution of an influence function foil rolling model [J]. International Journal of Mechanical Sciences, 2004, 46(8): 1139 − 1156. doi: 10.1016/j.ijmecsci.2004.08.006
[25] LE H R, SUTCLIFFE M P F. A robust model for rolling of thin strip and foil [J]. International Journal of Mechanical Sciences, 2001, 43(6): 1405 − 1419. doi: 10.1016/S0020-7403(00)00092-8
[26] LIU Y L, LEE W H. Mathematical model for the thin strip cold rolling and temper rolling process with the influence function method [J]. ISIJ International, 2005, 45(8): 1173 − 1178. doi: 10.2355/isijinternational.45.1173
[27] WU C H, ZHANG L C, QU P L, et al. Effect of the elastic deformation of rolls on the surface texture transfer in skin-pass rolling [J]. International Journal of Mechanical Sciences, 2021, 198: 106358. doi: 10.1016/j.ijmecsci.2021.106358
[28] 刘晓, 付伦, 芦跃峰, 等. 薄带材轧制的最小可轧厚度理论及数值模拟[J]. 钢铁, 2021, 56(11): 87 − 95. LIU Xiao, FU Lun, LU Yuefeng, et al. Theory and numerical simulation of minimum rolling thickness for thin strip rolling [J]. Iron and Steel, 2021, 56(11): 87 − 95. (in Chinese)
[29] XIAO H, REN Z K, LIU X. New mechanism describing the limiting producible thickness in ultra-thin strip rolling [J]. International Journal of Mechanical Sciences, 2017, 133: 788 − 793. doi: 10.1016/j.ijmecsci.2017.09.046
计量
- 文章访问数: 76
- HTML全文浏览量: 2
- PDF下载量: 9
