RESEARCH ON THE PROPAGATION CHARACTERISTICS OF GUIDED WAVES IN STEEL STRANDS
-
摘要:
导波作为一种有效的无损检测方法,在钢绞线检测中具有广阔的应用前景。钢绞线的特殊螺旋结构,使得导波在钢绞线中的传播性质尚未完全了解。该文研究了导波在七丝钢绞线中频散性质。利用Frenet-Serret方法建立了螺旋坐标系,在此基础上对传统半解析有限元方法进行了改进,得到了适用于螺旋结构的波导特征方程。计算了单根高强直钢丝的频散曲线,分析了导波的频散特性,研究了导波在七丝钢绞线中传播的频散特性,得到的频散曲线“陷频”现象中心频率与实验结果一致,并且钢绞线和直钢丝的频散曲线具有很大差异。通过钢绞线超声导波应力测试实验验证了该文所提出的螺旋半解析有限元法的正确性和有效性。结果表明,实验结果与理论群速度吻合良好,并且钢绞线的轴向应力与钢绞线中导波群速度近似线性关系。
Abstract:Guided waves, as an effective non-destructive testing method, have a broad application prospect in steel strand inspection. Due to the special spiral structure of steel strands, the propagation characteristics of guided waves in steel strands are not yet fully understood. The frequency dispersion property of guided waves in a seven-wire steel strand is investigated. The spiral coordinate system is established by using the Frenet-Serret method, and the traditional semi-analytical finite element method is improved to obtain the waveguide characteristic equation applicable to the spiral structure. Then the dispersion curves of a single high-strength straight steel wire are calculated, and the dispersion characteristics of the guided waves are analyzed. Meanwhile the dispersion characteristics of the guided wave propagating in a seven-wire strand are investigated, and the obtained dispersion curves are consistent with the experimental results in terms of the central frequency of the "trapping" phenomenon. There is a great difference in dispersion curves between the steel strand and the straight steel wire. Experiments to test the steel strand ultrasonic guided wave stress were undertaken to verify the correctness and effectiveness of the spiral semi-analytical finite element method proposed in this paper. The results show that the analytical group velocity is in good agreement with the experimental results, and the axial stress of the steel strand has an approximately linear relationship with the guided wave group velocity in the steel strand.
-
钢绞线是预应力结构和大跨度索承体系桥梁的核心受力构件,在土木工程领域有着广泛的应用[1 − 2]。然而,钢绞线长期暴露在环境中及其高应力条件下会导致其性能退化和结构失效。因此,有必要发展一种高效、精准的无损检测方法,以确定钢绞线中的应力水平。传统的应力检测方法有很多局限性,并不适用于钢绞线。导波作为一种新的无损检测技术,具有传播距离长、检测效率高、衰减低、对应力敏感等优点,在钢绞线检测中具有巨大的潜力[3 − 4]。
研究波导结构中导波频散特性是将导波技术运用于无损检测的基础。最早,Pochhammer-Chree方程对单根钢丝进行求解,实验已证明该方程并不适用于多根耦合的钢绞线[5 − 6]。由于钢绞线的特殊螺旋几何结构,超声导波在其中的传播特性无法利用传统的解析法获取;此外,考虑到钢绞线处于应力状态时,导波在钢绞线中的传播特性会受到影响,严重制约着超声导波技术在钢绞线中的推广应用。目前,国内外学者[7 − 9]主要采用数值方法获取钢绞线的传播特性。半解析有限元法是求解复杂结构中导波频散问题的有效方法[10 − 13]。由于钢绞线的螺旋几何形状和导线之间复杂的耦合关系,必须重新建立SAFE公式。FRIKHA等[14]在扭转坐标系中提出了SAFE方法,用于研究导波在钢绞线中的传播特性,并在群速度频散曲线中发现陷频现象,但未对该现象进行解释。LIU等[15]通过对波导截面采用高阶谱元离散化处理,利用比例边界有限元法得到了单根螺旋钢丝的频散曲线,分析了导波在螺旋波导中传播的截止频率、模态分离和模态转换的特性。对于同时存在着的曲线和直线的钢绞线,该方法并没有进一步拓展到钢绞线中。
本文基于Frenet-Serret方法建立了螺旋坐标系,在此坐标系下确定了协变与逆变基,随后在此坐标系下重新推导了SAFE方法,得到了适用于螺旋结构的波导特征方程,然后利用该方法研究导波在钢绞线中频散性质;最后,通过实验验证了本文提出的螺旋半解析有限法的正确性和有效性。
1 螺旋半解析有限元法
半解析有限元(semi-analytical finite element, SAFE)方法是用于研究任意截面的均匀直波导结构的一种有效方法,通过对波导截面进行有限元离散,沿波导传播方向的位移采用谐波指数函数的解析解方法进行处理[10]。与传统有限元方法相比,利用SAFE法研究导波频散特性计算效率得到显著提高,但是只适用于波导截面沿纵向直线方向是恒定不变的,并不适用于具有螺旋型的钢绞线,因此建立新SAFE方法,来研究钢绞线的特殊螺旋波导结构的传播特性。
1.1 螺旋坐标系
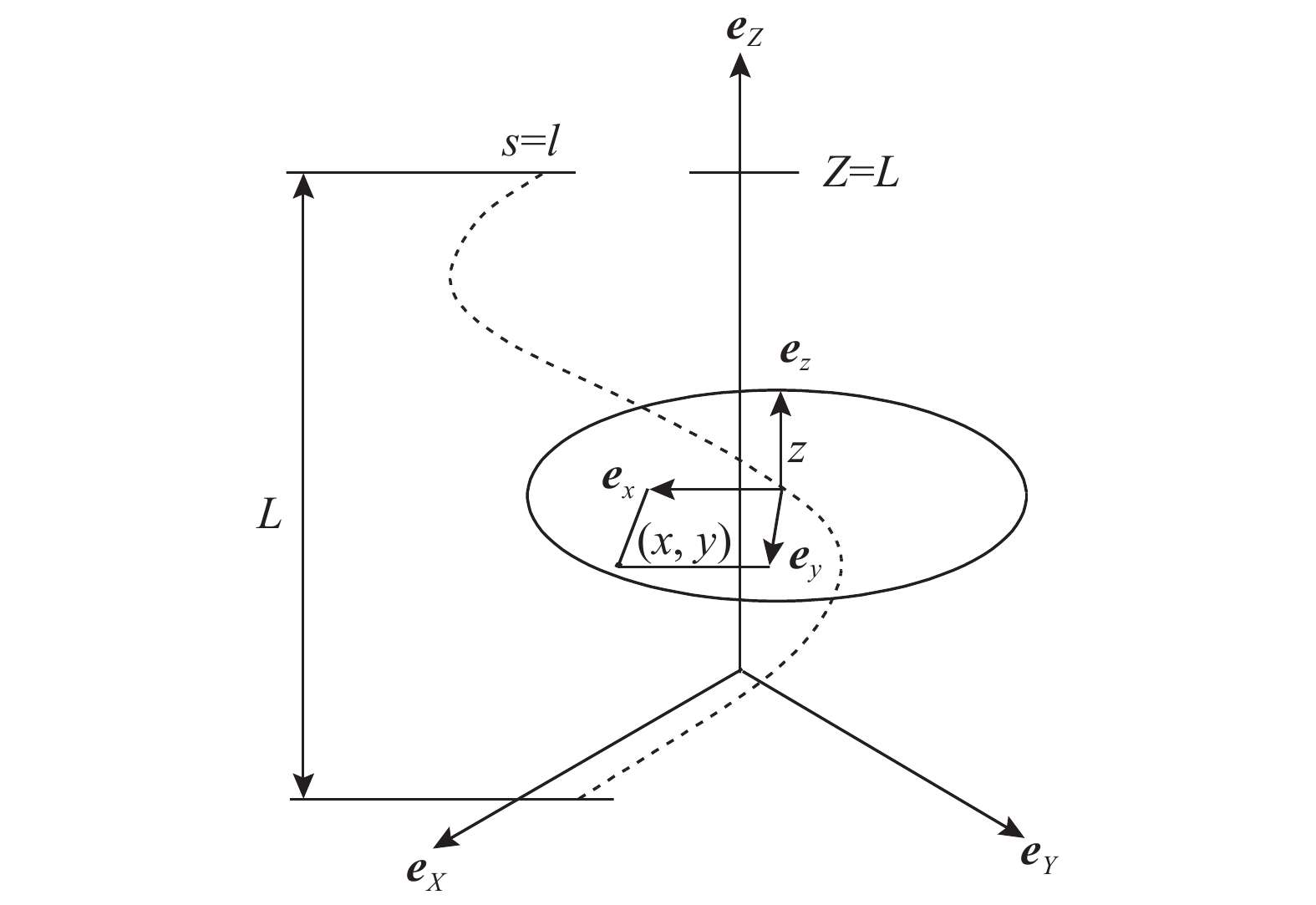
建立一种特殊曲线坐标系如图1所示,螺旋中心线r(s)表示为:
{\boldsymbol{r}}(s) = R\cos \left( {\frac{{2\pi }}{l}s + \theta } \right){{\boldsymbol{e}}_X} + R\sin \left( {\frac{{2\pi }}{l}s + \theta } \right){{\boldsymbol{e}}_Y} + \frac{L}{l}s{{\boldsymbol{e}}_Z} (1) 式中:R和(eX, eY, eZ)分别为笛卡尔(X, Y)平面螺旋半径和笛卡尔标准正交基向量;l = \sqrt {{L^2} - 4{\pi ^2}{R^2}} 和L分别为螺旋曲线长度和其对应的节距;θ为螺旋角度。
钢绞线中心线的单位正切向量、法向量和副法向量[16]分别表示为:
{\mathrm{d}}{\boldsymbol{T}}/{\mathrm{d}}s = \kappa {\boldsymbol{N}},{\mathrm{d}}{\boldsymbol{N}}/{\mathrm{d}}s = \tau {\boldsymbol{B}} - \kappa {\boldsymbol{T}},{\mathrm{d}}{\boldsymbol{B}}/{\mathrm{d}}s = - \tau {\boldsymbol{N}} (2) 式中,κ和τ为曲线的曲率及扭率,分别表示为 \kappa =2{\pi }^{2}R/{l}^{2},\tau =2\pi L/{l}^{2} 。
在笛卡尔坐标系中螺旋中心线(N, B, T)可利用Frenet-Serret公式表示为:
\begin{split} & {\boldsymbol{N}}(s) = \cos \left( {\frac{{2\pi }}{l}s + \theta } \right){{\boldsymbol{e}}_X} + \sin \left( {\frac{{2\pi }}{l}s + \theta } \right){{\boldsymbol{e}}_Y} \;,\\& {\boldsymbol{B}}(s) = - \frac{L}{l}\sin \left( {\frac{{2\pi }}{l}s + \theta } \right){{\boldsymbol{e}}_X} + \frac{L}{l}\cos \left( {\frac{{2\pi }}{l}s + \theta } \right){{\boldsymbol{e}}_Y} - \frac{{2\pi R}}{l}{{\boldsymbol{e}}_Z} \;,\\& {\boldsymbol{T}}(s) = - \frac{{2\pi R}}{l}\sin \left( {\frac{{2\pi }}{l}s + \theta } \right){{\boldsymbol{e}}_X} + \\&\qquad \frac{{2\pi R}}{l}\cos \left( {\frac{{2\pi }}{l}s + \theta } \right){{\boldsymbol{e}}_Y} - \frac{L}{l}{{\boldsymbol{e}}_Z} \\[-1pt] \end{split} (3) 利用上述方法,可以根据标准正交基(N, B, T)建立起新坐标系,其中任意位置向量在螺旋坐标系中可以表示为:
{\boldsymbol{X}}(x,y,s) = {\boldsymbol{R}}(s) + x{\boldsymbol{N}}(s) + y{\boldsymbol{B}}(s) (4) 式(3)中的非正交协变基 ({\boldsymbol{G}}_{1},{\boldsymbol{G}}_{2},{\boldsymbol{G}}_{3}) 可以通过 ({\boldsymbol{G}}_{1},{\boldsymbol{G}}_{2},{\boldsymbol{G}}_{3})=(\partial {\boldsymbol{X}}/\partial x,\partial {\boldsymbol{X}}/\partial y,\partial {\boldsymbol{X}}/\partial s) 映射方式得到:
\begin{split} & {{\boldsymbol{G}}_1} = {\boldsymbol{N}}(s)\;,\;{{\boldsymbol{G}}_2} = {\boldsymbol{B}}(s) \;,\\& {{\boldsymbol{G}}_3} = - \tau y{\boldsymbol{N}}(s) + \tau x{\boldsymbol{B}}(s) + (1 + \kappa x){\boldsymbol{T}}(s) \end{split} (5) 定义Gmn为协变度规张量,可由Gmn=GmGn计算得到:
{\boldsymbol{G}} = \left[ {\begin{array}{*{20}{c}} 1&0&{ - \tau y} \\ 0&1&{\tau x} \\ { - \tau y}&{\tau x}&{{\tau ^2}({x^2} + {y^2}) + {{(1 + \kappa x)}^2}} \end{array}} \right] (6) 式中,κ和τ为常数,因此G与螺旋坐标系s无关,说明在螺旋坐标系上任意截面上导波沿螺旋中心s方向保持不变,即该螺旋坐标系具有在s方向平移不变性,同时在所定义的坐标系中表示的任何偏微分算子的系数也与s无关。
基于上述的张量关系,在逆变基下,应变位移关系改写为:
\varepsilon = \left( {{{\boldsymbol{L}}_{xy}} + {{\boldsymbol{L}}_s}\frac{\partial }{{\partial s}}} \right){\boldsymbol{u}} (7) 式中,Lxy、Ls为微分算子。
考虑钢绞线为各向同性材料,对波导截面进行有限元离散化,根据哈密顿原理,最终得到含节点位移列向量U的特征值问题如下:
[ {{{\boldsymbol{K}}_1} + ik({{\boldsymbol{K}}_2} - {\boldsymbol{K}}_2^{\mathrm{T}}) + {k^2}{{\boldsymbol{K}}_3} - {\omega ^2}{\boldsymbol{M}}} ]{\boldsymbol{U}} = 0 (8) 其中:
\begin{split} & {\boldsymbol{K}}_1^e = \int_{{{\mathrm{S}}^{\mathrm{e}}}} {{{({{\boldsymbol{L}}_{xy}}N)}^{\mathrm{T}}}{\boldsymbol{D}}D{{\boldsymbol{L}}_{xy}}{\boldsymbol{N}}\sqrt {\boldsymbol{G}} {\mathrm{d}}s} ,\\& {\boldsymbol{K}}_2^e = \int_{{{\mathrm{S}}^{\mathrm{e}}}} {{{({{\boldsymbol{L}}_{xy}}{\boldsymbol{N}})}^{\mathrm{T}}}{\boldsymbol{D}}{{\boldsymbol{L}}_s}{\boldsymbol{N}}\sqrt {\boldsymbol{G}} {\mathrm{d}}s} \\& {\boldsymbol{K}}_3^e = \int_{{{\mathrm{S}}^{\mathrm{e}}}} {{{({{\boldsymbol{L}}_s}{\boldsymbol{N}})}^{\mathrm{T}}}{\boldsymbol{D}}{{\boldsymbol{L}}_s}{\boldsymbol{N}}\sqrt {\boldsymbol{G}} {\mathrm{d}}s} ,\\& {{\boldsymbol{M}}^e} = \int_{{{\mathrm{S}}^{\mathrm{e}}}} {\rho {{\boldsymbol{N}}^{\mathrm{T}}}{\boldsymbol{N}}\sqrt {\boldsymbol{G}} {\mathrm{d}}s} \end{split} (9) 式中:K1、K2、K3为系统刚度矩阵; {K}_{1}^{{\mathrm{e}}}、{K}_{2}^{{\mathrm{e}}}、{K}_{3}^{{\mathrm{e}}} 为各单元刚度矩阵;M为系统质量矩阵;Me为单元质量矩阵。
求解式(8),可得到某一频率\omega 对应的特征值k和特征向量U。根据频率\omega 和对应的特征值k,求得导波在钢绞线中传播的相速度Cp与群速度Cg分别为:
{C_{\mathrm{p}}} = \frac{\omega }{k} (10) {C_{\mathrm{g}}} = \frac{{{{\boldsymbol{U}}^{\text{T}}}( {i({{\boldsymbol{K}}_2} - {{\boldsymbol{K}}_2}^{\text{T}}) + 2k{{\boldsymbol{K}}_3}} ){\boldsymbol{U}}}}{{2\omega {{\boldsymbol{U}}^{\text{T}}}{\boldsymbol{MU}}}} (11) 2 直钢丝导波特性分析
钢绞线是由中间钢丝和外围的螺旋钢丝共同构成的。首先,考虑直径为5 mm高强度直钢丝的弹性模量E=210 GPa,泊松比μ=0.3,密度ρ=7850 kg/m3,扭率τ=0。利用式(8)、式(10)可以得到单根直钢丝的频散曲线。
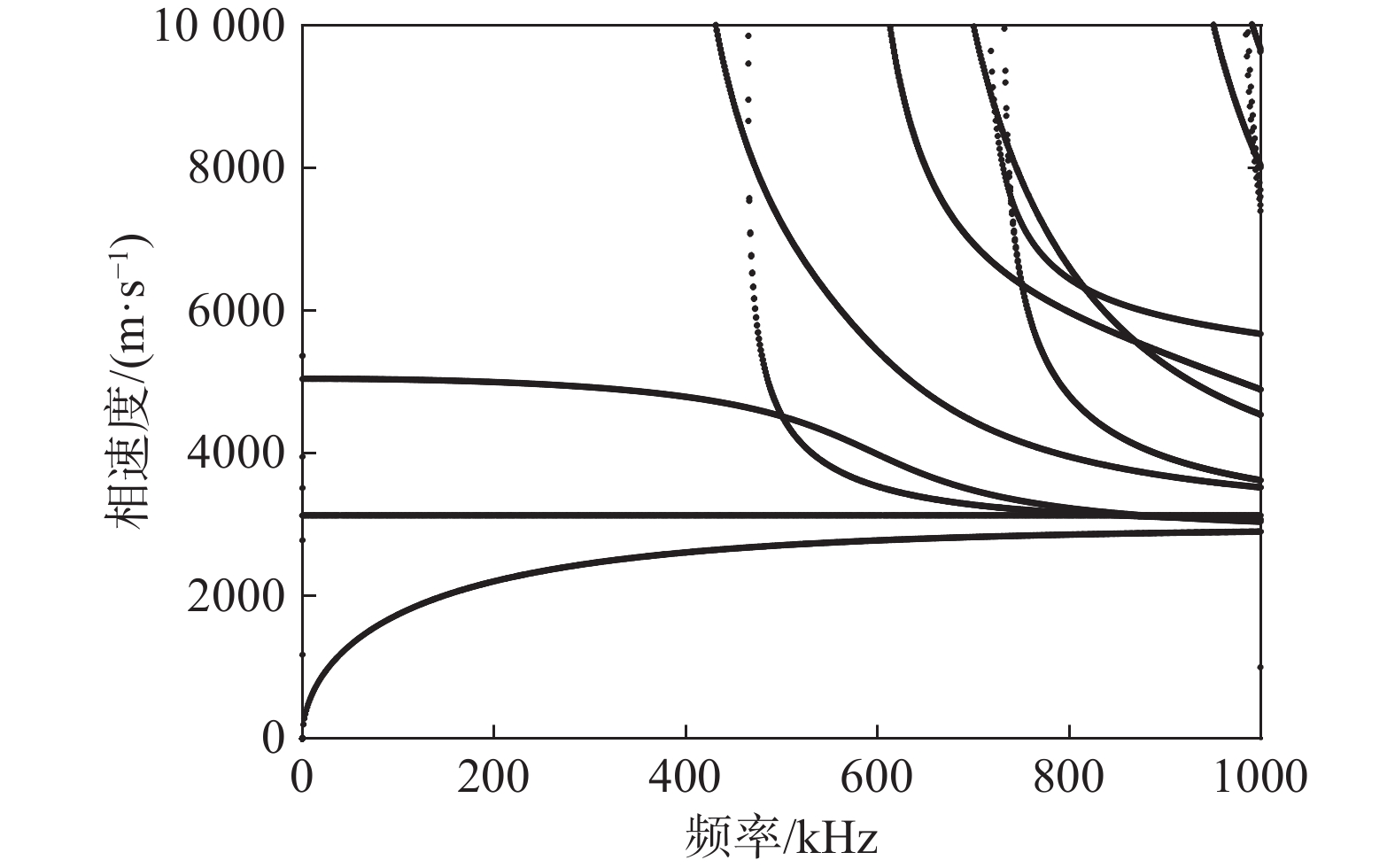
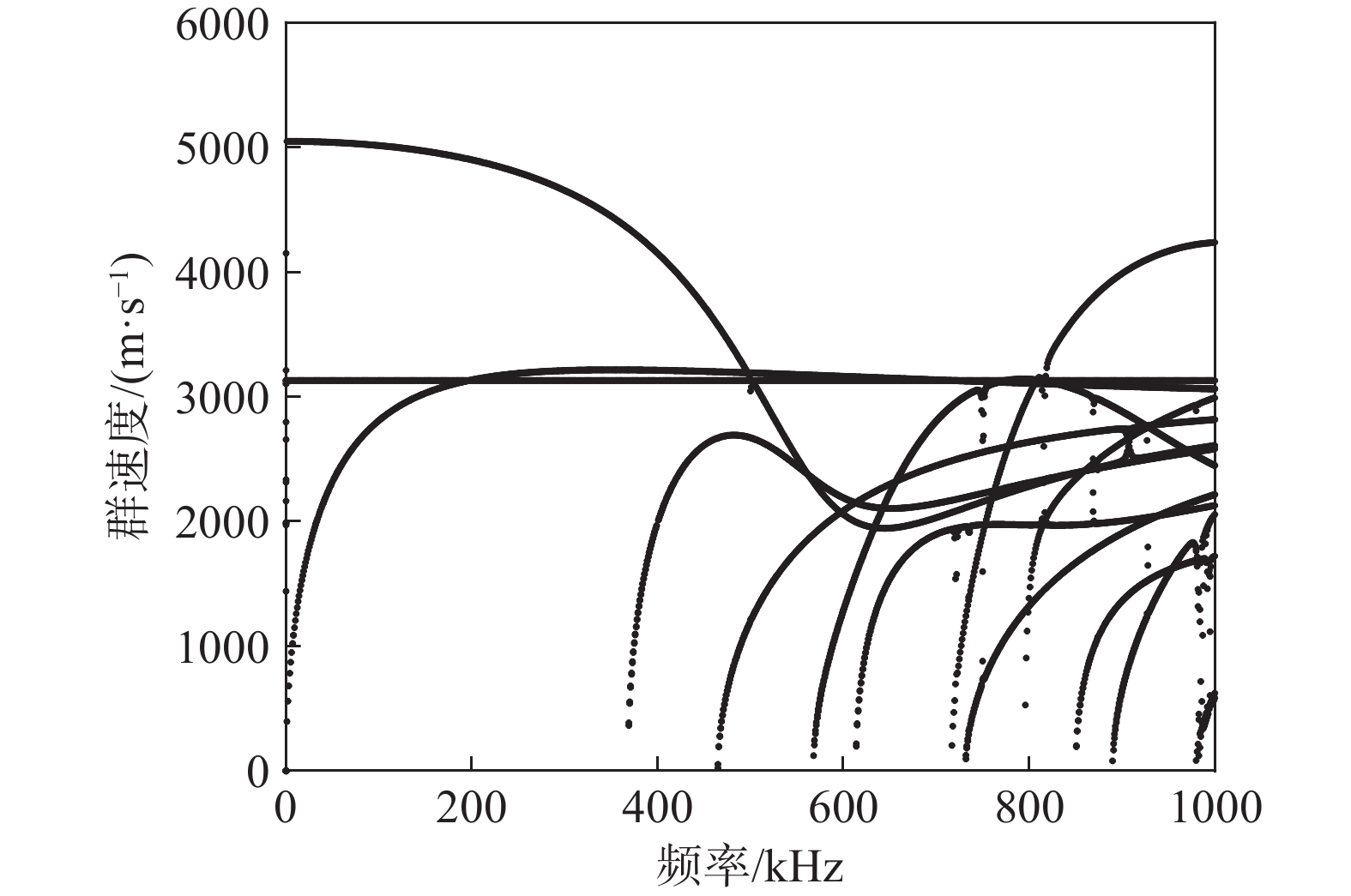
从图2~图3可知,导波在单根直钢丝中传播时,存在三种基本模态分别为纵向模态、扭转模态、弯曲模态,其中只有扭转模态未发生频散现象,并且随着频率的增加,各模态频散程度不同。同时L(0,1)模态在400 kHz以内时,群速度大于其他模态,这说明采用该模态进行激励时能够最先接收到信号,利于后续对信号的分离处理。
3 七丝钢绞线导波特性分析
对七丝钢绞线截面进行有限元网格划分,其中钢绞线中心钢丝半径为2.575 mm,外围螺旋钢丝半径为2.5 mm,扭率为\tau = 2\pi L/{l^2},线间接触采用赫兹接触,其余模型参数同上节高强钢丝。
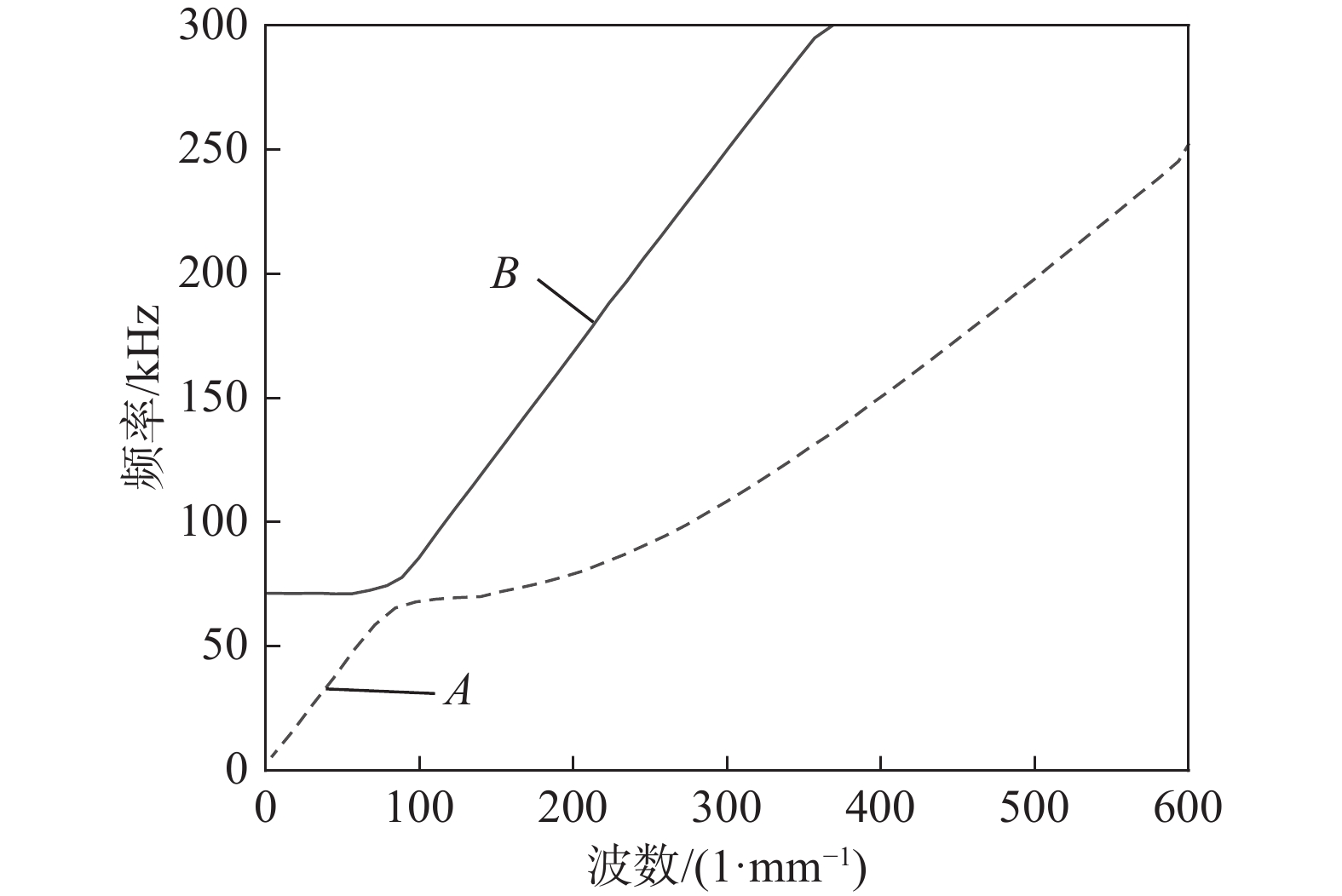
图4给出了七丝钢绞线导波的群速度频散曲线,与单根高强直钢丝相比,由于钢绞线特殊螺旋结构和线间的相互作用,增加了许多新模态,导波特性也更加复杂。特别是在低频率时,L(0,1)、T(0,1)、F(1,1)模态均出现了频率截止现象。随着频率的增加,弯曲模态出现分支现象,并且频率越高模态分支越剧烈,在钢绞线的检测应用时,应该尽量避免在该频率区域。值得注意的是在群速度曲线上出现频率凹陷现象,也被称为“陷频”。利用模态正交性方法提取L(0,1)模态,清晰显示了该模态的截断中心频率大约为70 kHz,这与文献[9]在实验中观察到的缺口频率现象一致。图5表明两条波数在缺口频率附近先相互靠近,然后迅速排斥偏离,两条波数并没有产生交叉现象,此时出现了频散特性的转换。
为了进一步研究陷频现象,提取图中A、B两点的振型如图6、图7所示。由于结构是对称的,得到的振型也是对称的,并且其振型发生了改变,变得更加复杂。
4 实验验证
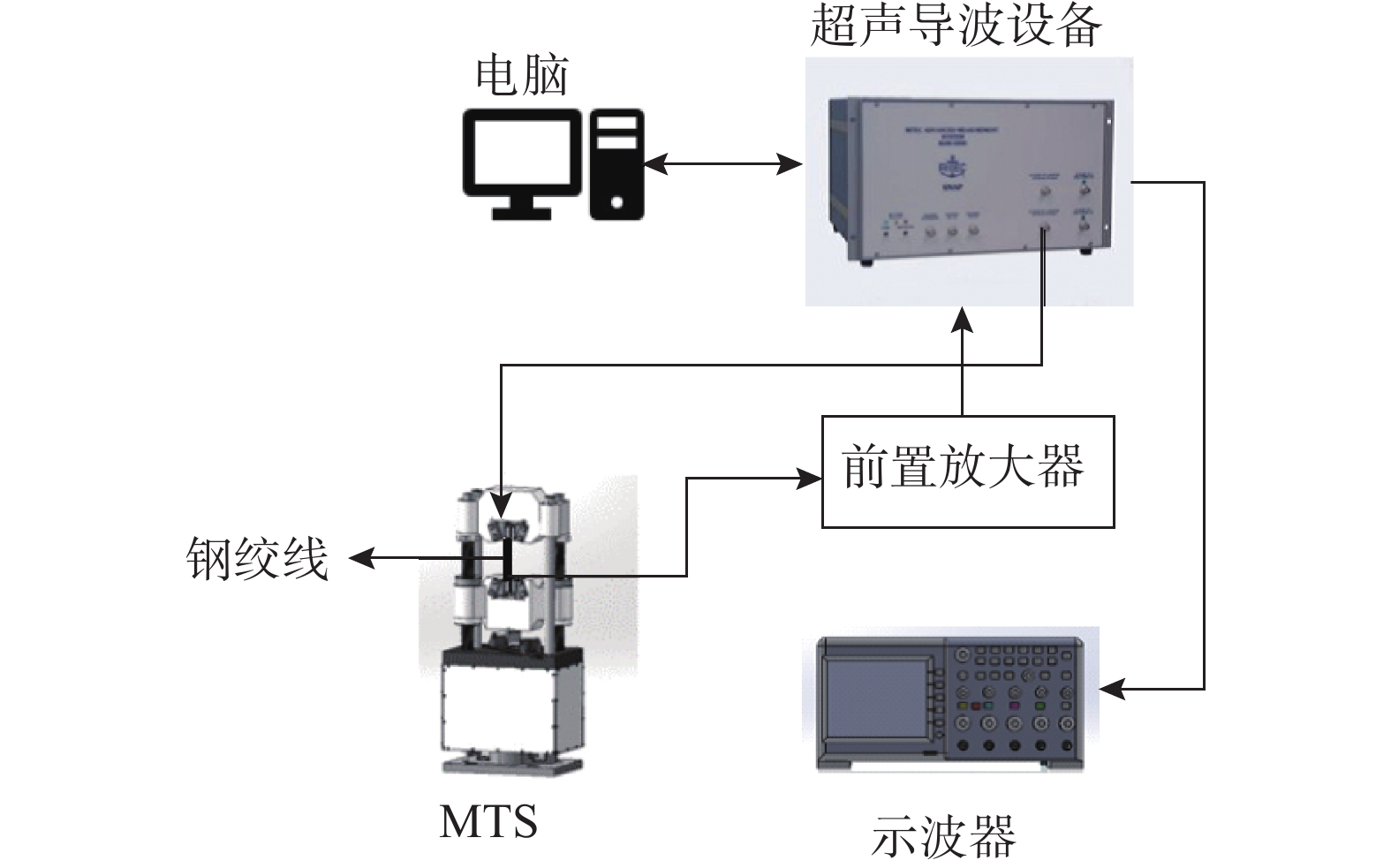
为验证本文提出的螺旋半解析有限元法的准确性,搭建了钢绞线超声导波实验测试平台,实验选取直径为15.2 mm、长度为59.0 mm的钢绞线作为试件,极限抗拉强度为1800 MPa。然后,设计了如图8所示的实验原理,同时整个实验设置实际连接图,如图9所示。最后,基于非线性导波装置开展钢绞线拉伸实验,利用MTS万能试验机对钢绞线施加不同水平的应力,采集相应的导波激励与接收信号。
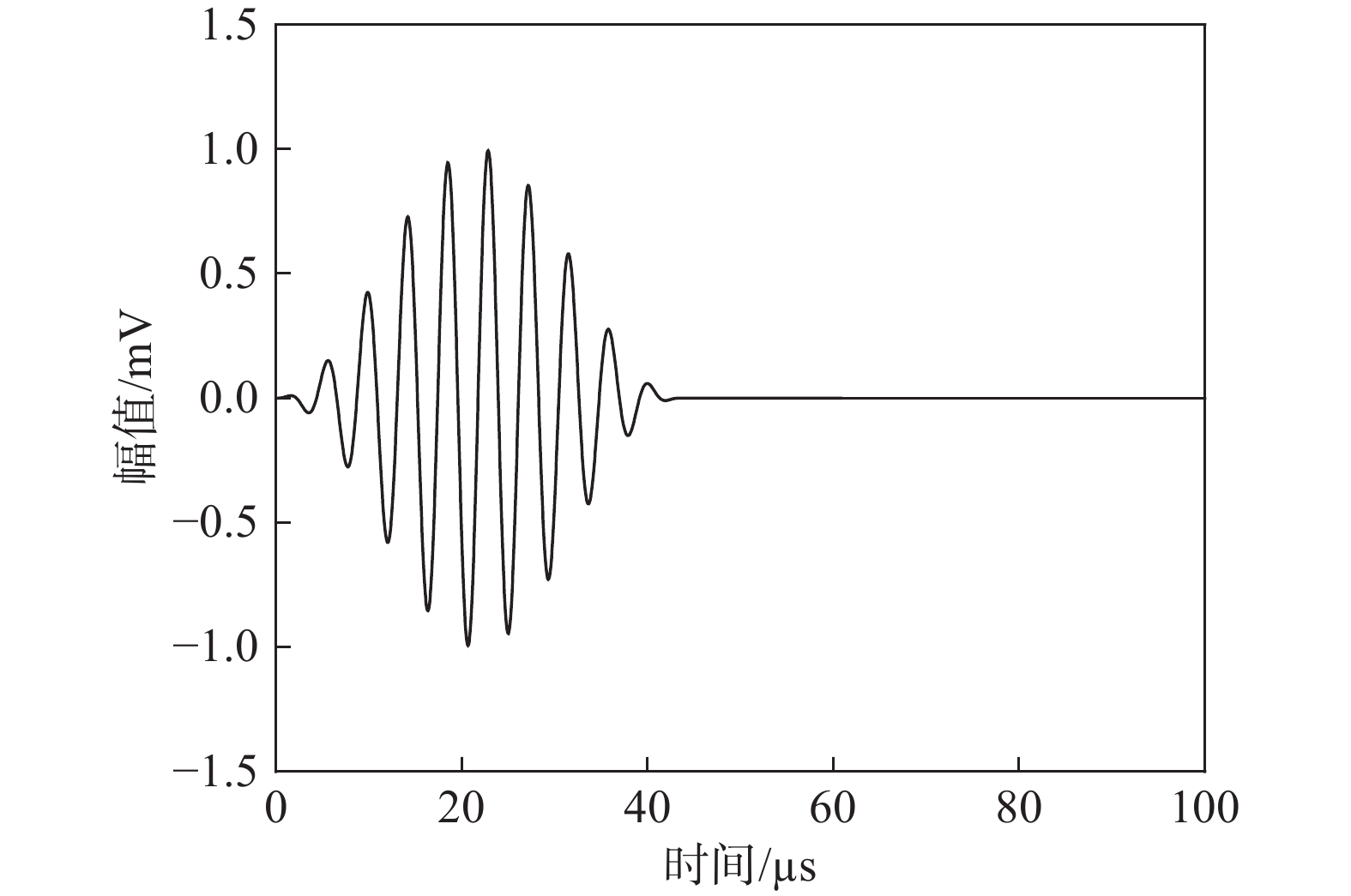
实验采用了由汉宁窗口调制的中心频率为230 kHz、周期数为10的正弦信号作为导波的激励信号,如图10所示,其中传感器PZT4选择了横截面黏贴。
钢绞线实验的激励与接收信号如图11所示。飞行时间由激励信号的波包的峰值点和接收信号的第一波包的峰值之间的差来确定。随后根据试件长度与飞行时间,即可算出实验中不同应力水平下的导波群速度,如表1所示。
表 1 修正后230 kHz下不同应力导波波速Table 1. Corrected wave speeds of different stress guided waves at 230 kHz轴向拉应力/MPa 理论群速度/(m/s) 实验群速度/(m/s) 差值/(m/s) 误差/(%) 0 4891.47 4798.32 93.15 1.90 100 4887.23 4794.48 92.75 1.90 200 4884.98 4790.70 94.28 1.93 300 4881.72 4786.81 94.91 1.94 400 4878.46 4781.90 96.56 1.98 500 4875.20 4775.84 99.36 2.04 600 4872.94 4771.49 101.45 2.08 700 4869.67 4768.78 100.89 2.07 800 4866.39 4766.35 100.04 2.06 900 4863.11 4764.35 98.76 2.03 1000 4860.83 4761.68 99.15 2.04 由图11可知,激励信号并不受应力的影响;而接收信号受应力的影响较大。随着应力的增大,接收信号的幅值和波形发生了明显的变化,并且导波信号逐渐后移。这是由于钢绞线在轴向荷载的作用下外围钢丝和中间钢丝之间发生了相互挤压。
从表1中结果可知随着拉应力的增加,导波理论与实验的群速度均逐渐减少,但两者群速度之间有一定的差距。这是由于钢绞线中存在残余应力,并且理论计算采用的弹性模量与泊松比与实际的钢绞线存在着一定的差距。通过本文所提出的方法获得的群速度与相应的实验结果匹配地很好。理论值和实验值之间的最大相对误差通常小于2.1%,平均绝对相对误差为2%,这证明了使用本文的方法计算群速度的准确性。
5 结论
本文基于Frenet-Serret方法建立了螺旋坐标系,在此坐标系下重新推导了SAFE方法,得到了适用于螺旋结构的波导特征方程,然后利用该方法研究了导波在钢绞线中频散性质,最后通过钢绞线超声导波实验验证了本文提出的方法的正确性,可以得出以下结论:
(1)钢绞线在导波激励下,存在三种基本模态分别是纵向、弯曲、扭转模态,频率越高,导波传播模态种类越多,频散现象越严重;
(2)与单根高强直钢丝相比,导波在七丝钢绞线中的传播更加复杂,特别是在群速度曲线中出现了截止频率、模态分支和陷频现象,在实际运用中应该避免三者的频率区域;
(3)利用本文的方法获得的钢绞线理论群速度与实验群速度结果吻合良好,证实了本文方法的精确性,能够满足对钢绞线的导波频散特性研究。
-
表 1 修正后230 kHz下不同应力导波波速
Table 1 Corrected wave speeds of different stress guided waves at 230 kHz
轴向拉应力/MPa 理论群速度/(m/s) 实验群速度/(m/s) 差值/(m/s) 误差/(%) 0 4891.47 4798.32 93.15 1.90 100 4887.23 4794.48 92.75 1.90 200 4884.98 4790.70 94.28 1.93 300 4881.72 4786.81 94.91 1.94 400 4878.46 4781.90 96.56 1.98 500 4875.20 4775.84 99.36 2.04 600 4872.94 4771.49 101.45 2.08 700 4869.67 4768.78 100.89 2.07 800 4866.39 4766.35 100.04 2.06 900 4863.11 4764.35 98.76 2.03 1000 4860.83 4761.68 99.15 2.04 -
[1] 陈鑫, 朱劲松, 钱骥, 等. 基于导波多尺度能量熵的钢绞线张拉力识别[J]. 振动、测试与诊断, 2020, 40(4): 745 − 750. CHEN Xin, ZHU Jingsong, QIAN Ji, et al. Steel strands tension identification using multi-scale energy entropy of ultrasonic guided waves [J]. Journal of Vibration, Measurement & Diagnosis, 2020, 40(4): 745 − 750. (in Chinese)
[2] 杜咏, 孙亚凯, 李国强. 预应力钢绞线高温力学性能试验研究[J]. 工程力学, 2019, 36(4): 231 − 238. doi: 10.6052/j.issn.1000-4750.2018.03.0141 DU Yong, SUN Yakai, LI Guoqiang. Mechanical properties of high tensile steel cables at elevated temperature [J]. Engineering Mechanics, 2019, 36(4): 231 − 238. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.03.0141
[3] CHEN H P, ZHOU H, YE L. Dispersive modal characteristics of guided waves propagating in damaged rails [J]. Journal of Aerospace Engineering, 2023, 36(3): 04023001. doi: 10.1061/JAEEEZ.ASENG-4779
[4] CHEN H P, ZHANG G Y, HU W C, et al. Nondestructive determination of longitudinal rail stress from guided wave dispersion properties [J]. Construction and Building Materials, 2023, 408: 133618. doi: 10.1016/j.conbuildmat.2023.133618
[5] GAZIS D C. Three-dimensional investigation of the propagation of waves in hollow circular cylinders. I. Analytical foundation [J]. The Journal of the Acoustical Society of America, 1959, 31(5): 568 − 573. doi: 10.1121/1.1907753
[6] KWUN H, BARTELS K A, HANLEY J J. Effects of tensile loading on the properties of elastic-wave propagation in a strand [J]. The Journal of the Acoustical Society of America, 1998, 103(6): 3370 − 3375. doi: 10.1121/1.423051
[7] LIU X C, WU B, QIN F, et al. Observation of ultrasonic guided wave propagation behaviours in pre-stressed multi-wire structures [J]. Ultrasonics, 2017, 73: 196 − 205. doi: 10.1016/j.ultras.2016.08.014
[8] 钱骥, 李健斌, 乔珍珍, 等. 基于非线性超声混频技术的钢绞线张力识别研究[J]. 振动与冲击, 2022, 41(7): 116 − 125. QIAN Ji, LI Jianbin, QIAO Zhenzhen, et al. Identification of steel strand tension based on nonlinear ultrasonic frequency-mixing technology [J]. Journal of Vibration and Shock, 2022, 41(7): 116 − 125. (in Chinese)
[9] TREYSSÈDE F, LAGUERRE L. Investigation of elastic modes propagating in multi-wire helical waveguides [J]. Journal of Sound and Vibration, 2010, 329(10): 1702 − 1716. doi: 10.1016/j.jsv.2009.11.021
[10] HAYASHI T. Guided wave dispersion curves derived with a semianalytical finite element method and its applications to nondestructive inspection [J]. Japanese Journal of Applied Physics, 2008, 47(5S): 3865 − 3870. doi: 10.1143/JJAP.47.3865
[11] LI W X, DWIGHT R A, ZHANG T L. On the study of vibration of a supported railway rail using the semi-analytical finite element method [J]. Journal of Sound and Vibration, 2015, 345: 121 − 145. doi: 10.1016/j.jsv.2015.01.036
[12] LOVEDAY P W. Semi-analytical finite element analysis of elastic waveguides subjected to axial loads [J]. Ultrasonics, 2009, 49(3): 298 − 300. doi: 10.1016/j.ultras.2008.10.018
[13] 胡剑虹, 唐志峰, 吕福在, 等. 基于SAFE的层状结构导波传播特性研究[J]. 工程力学, 2014, 31(11): 218 − 224. doi: 10.6052/j.issn.1000-4750.2013.05.0457 HU Jianhong, TANG Zhifeng, LU Fuzai, et al. Research of guided waves in layered structures based on safe [J]. Engineering Mechanics, 2014, 31(11): 218 − 224. (in Chinese) doi: 10.6052/j.issn.1000-4750.2013.05.0457
[14] FRIKHA A, CARTRAUD P, TREYSSÈDE F. Mechanical modeling of helical structures accounting for translational invariance. Part 1: Static behavior [J]. International Journal of Solids and Structures, 2013, 50(9): 1373 − 1382. doi: 10.1016/j.ijsolstr.2013.01.010
[15] LIU Y J, HAN Q, LI C L, et al. Numerical investigation of dispersion relations for helical waveguides using the scaled boundary finite element method [J]. Journal of Sound and Vibration, 2014, 333(7): 1991 − 2002. doi: 10.1016/j.jsv.2013.11.041
[16] ABBENA E, SALAMON S, GRAY A. Modern differential geometry of curves and surfaces with mathematica [M]. 3rd ed. New York: CRC Press, 2017.



 下载:
下载: