MACRO AND MICRO DAMAGE OF CONCRETE GRAVITY DAM UNDER EARTHQUAKE ACTION BASED ON SUBMODEL METHOD
-
摘要:
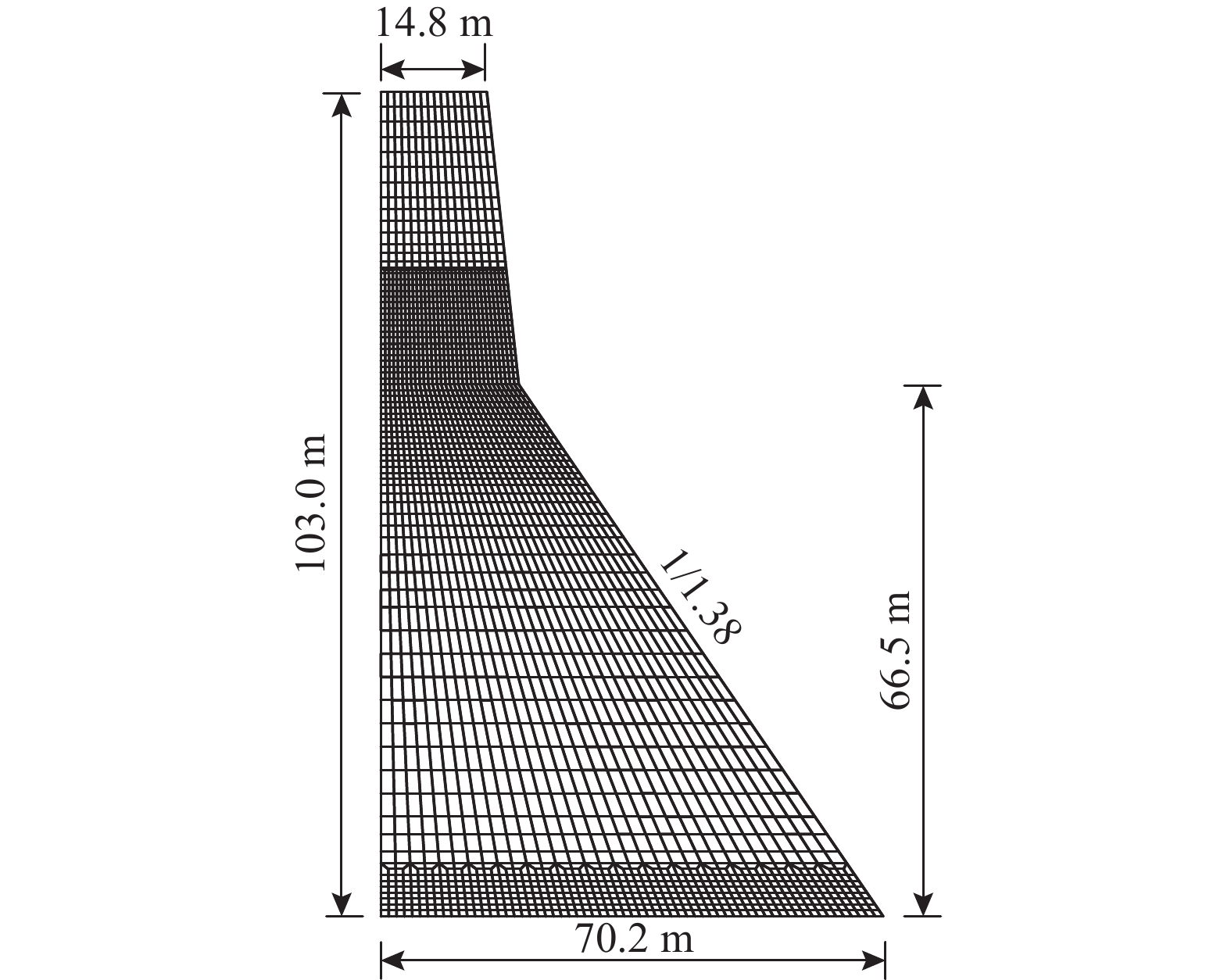
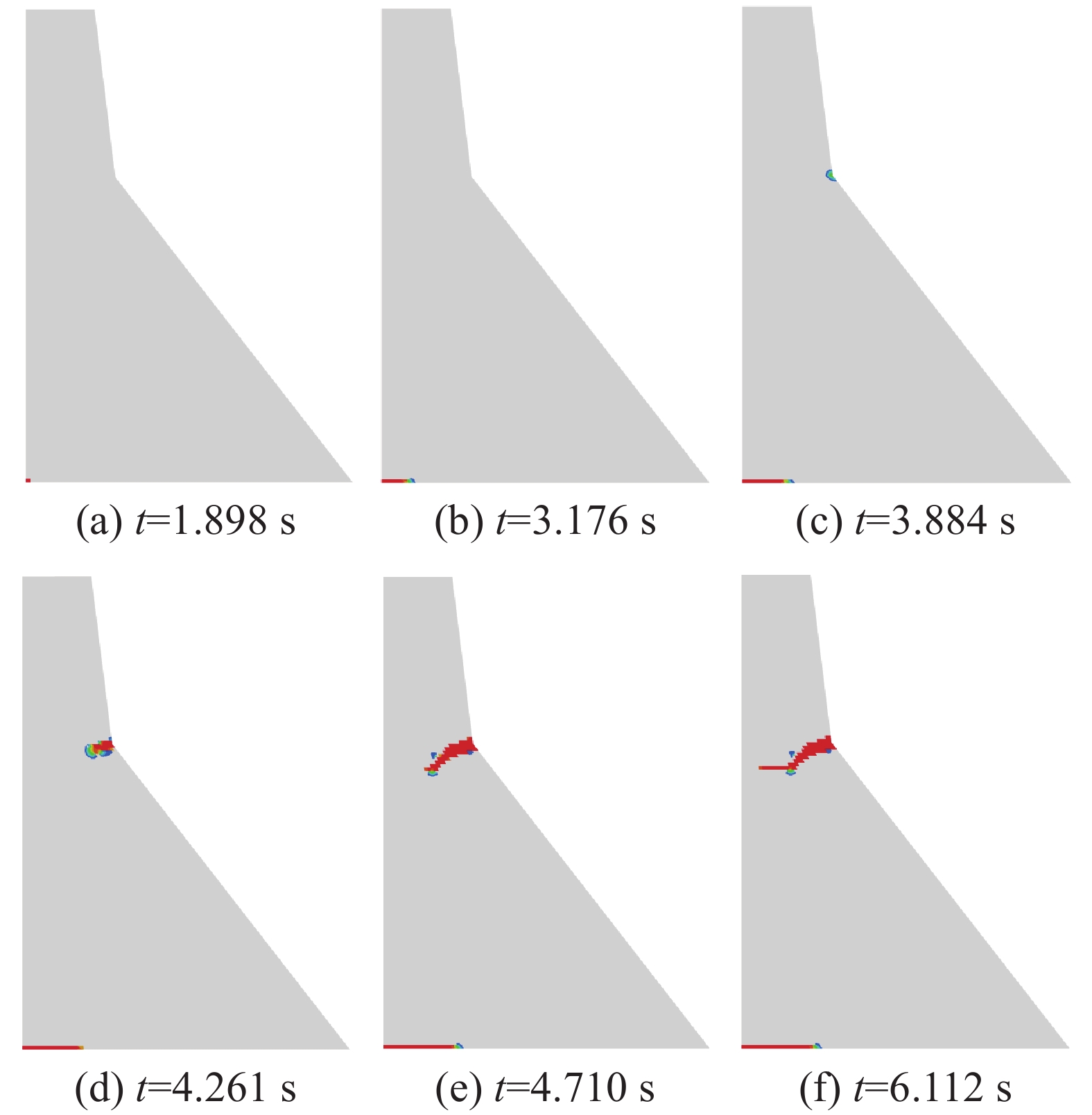
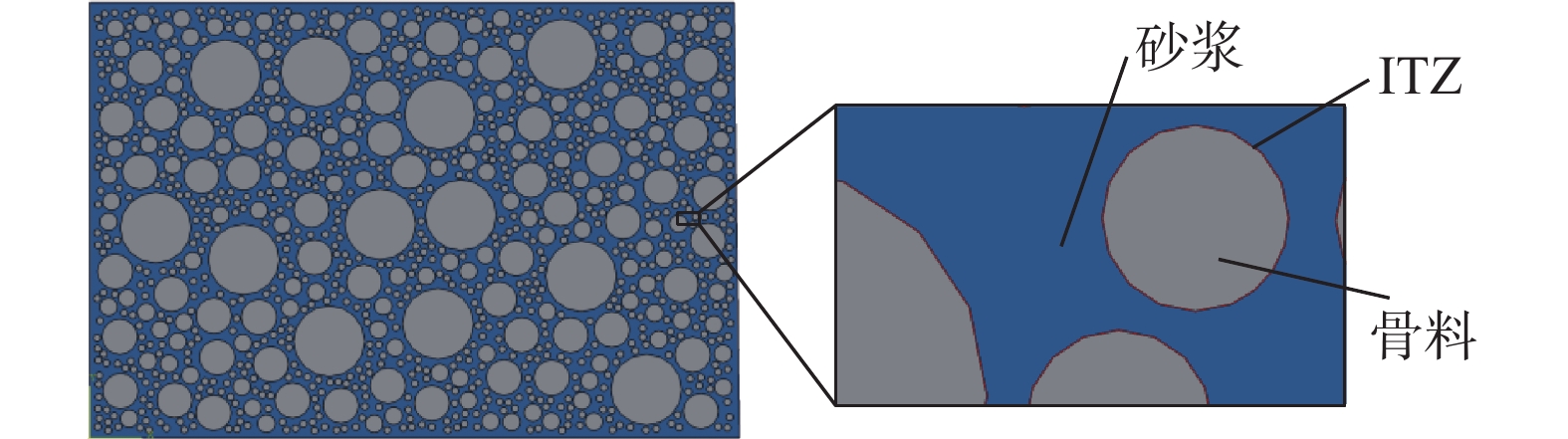
大型水工混凝土结构易在结构突变部位出现应力集中现象，工程结构的整体失效破坏起源于局部区域的损伤积累和裂缝失稳扩展。为明确混凝土重力坝在地震荷载作用下的力学特性，采用子模型法构建了基于实际工程的重力坝坝踵高应力区的精细化模型。基于坝踵代表体的细观结构模型，研究了地震作用下重力坝局部受力变形特征以及损伤演变过程。研究结果表明：与宏观模型计算结果相比，细观子模型计算结果能够更真实地反映应力场，位移场，裂纹分布以及损伤演变过程。此外，研究发现细观结构内部的损伤发生时间早于宏观结构，表明宏观裂缝源于内部，混凝土结构破坏并非瞬间完成，而是由于其内部微细裂纹的演化形成更大的宏观裂缝导致。研究结果为重力坝宏观和细观尺度的损伤分布形式提供参考和借鉴。
Abstract:Large hydraulic concrete structures are prone to stress concentration at points of structural discontinuity. The overall failure of engineering structures originates from damage accumulation and crack instability extension in local areas. To clarify the mechanical properties of concrete gravity dams under seismic loading, this study adopts the submodel method to construct a refined model of the high stress zone in the heel of gravity dams based on actual engineering projects. On the basis of the meso structural model of the representative element of the dam heel, the local force deformation characteristics and damage evolution process of the gravity dam under seismic action are studied. It shows that the results of the meso submodel can more realistically reflect the stress field, displacement field, crack distribution and damage evolution process than the macro model. In addition, it finds that the damage occurrence in the meso structure is earlier than in the macro structure. This indicates that the macro cracks originate from the inside, and the destruction of concrete structure is not instantaneous, but caused by the evolution of its internal microcracks to form larger macrocracks. These results provide a reference for the formation and distribution of the damage of gravity dams at macro and meso scales.
-
Keywords:
- concrete gravity dam /
- seismic load /
- mechanical properties /
- submodel method /
- damage evolution
-
-
![]()
图 1 CDP模型单轴应力-应变关系曲线
Figure 1. Uniaxial stress-strain relationship curve for the CDP model
![]()
图 2 Koyna大坝最高坝段有限元模型
Figure 2. Finite element model of the highest section of Koyna dam
![]()
图 4 Koyna重力坝最大主应力分布等值线云图和位移分布等值线云图
Figure 4. Contour map of the distribution of the maximum principal stress and displacement for Koyna dam
![]()
图 5 数值模拟和模型试验下的Koyna大坝最终失效模式
Figure 5. Final failure modes of Koyna dam via the method of numerical simulation and model test
![]()
图 6 地震作用下的Koyna大坝损伤随时间演变的过程
Figure 6. Damage evolution of Koyna dam under seismic action over time
![]()
图 7 利用子模型法进行坝踵代表体单元宏观再细化分析
Figure 7. Macro-refinement analysis of a representative element at the dam heel using the submodel method
![]()
图 9 坝踵代表体单元的细观结构模型
Figure 9. Mesoscale structural model of the representative element at the dam heel
![]()
图 11 细观子模型再计算损伤随时间的演变过程
Figure 11. Damage evolution over time in the recalculated mesoscale submodel
表 1 混凝土细观组分的力学参数
Table 1 Mechanical properties of the mesoscale components of concrete
组分参数 骨料 砂浆 ITZ 弹性模量/GPa 80 25 20 泊松比ν 0.16 0.22 0.2 剪胀角Ψ/(°) 30 30 偏心率η 0.1 0.1 受拉子午线与受压子午线常应力的比值Kc 0.667 0.667 应力比¯σcc/¯σc 1.16 1.16 抗拉强度ft/MPa 3 2.4 抗压强度fc/MPa 45 36 裂纹极限宽度wc/mm 0.096 0.096 
下载: 导出CSV
-
[1] 任青文. 灾变条件下高拱坝整体失效分析的理论与方法[J]. 工程力学, 2011, 28(增刊2): 85 − 96. REN Qingwen. Theory and methods of high arch dam’s entire failure under disaster conditions [J]. Engineering Mechanics, 2011, 28(Suppl 2): 85 − 96. (in Chinese)
[2] 顾嘉丰, 任青文. 水工混凝土弥散型裂缝数值模型中开裂判据的研究[J]. 工程力学, 2015, 32(6): 84 − 91. doi: 10.6052/j.issn.1000-4750.2013.12.1141 GU Jiafeng, REN Qingwen. Study on hydraulic concrete cracking criterion in smeared crack numerical model [J]. Engineering Mechanics, 2015, 32(6): 84 − 91. (in Chinese) doi: 10.6052/j.issn.1000-4750.2013.12.1141
[3] 邱莉婷, 马福恒, 沈振中, 等. 大坝混凝土楔入劈拉试验的并发多尺度区域分解数值模拟[J]. 水利水电技术, 2019, 50(8): 195 − 202. QIU Liting, MA Fuheng, SHEN Zhenzhong, et al. Numerical simulation of concurrent multiscale domain decomposition for dam concrete wedge splitting test [J]. Water Resources and Hydropower Engineering, 2019, 50(8): 195 − 202. (in Chinese)
[4] 崔磊, 毛江鸿, 金伟良, 等. 基于多边界切割插值的改进子模型分析方法[J]. 计算力学学报, 2015, 32(5): 619 − 626. CUI Lei, MAO Jianghong, JIN Weiliang, et al. Improved sub-model analysis based on cut-boundary of multiple interpolation [J]. Chinese Journal of Computational Mechanics, 2015, 32(5): 619 − 626. (in Chinese)
[5] 赵大亮, 李爱群, 丁幼亮, 等. 基于子模型法的大跨斜拉桥扁平钢箱梁应力分析[J]. 计算力学学报, 2008, 25(3): 326 − 332. ZHAO Daliang, LI Aiqun, DING Youliang, et al. Stress analysis on steel-box girder of long span cable-stayed bridge based on submodei method [J]. Chinese Journal of Computational Mechanics, 2008, 25(3): 326 − 332. (in Chinese)
[6] 张雨霆, 肖明, 张志国. 大型地下洞室群地震响应分析的动力子模型法[J]. 岩石力学与工程学报, 2011, 30(增刊2): 3392 − 3400. ZHANG Yuting, XIAO Ming, ZHANG Zhiguo. Dynamic sub-model method of earthquake response analysis of large-scale underground caverns [J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(Suppl 2): 3392 − 3400. (in Chinese)
[7] 耿萍, 郭翔宇, 王琦, 等. 基于子模型法的盾构隧道纵向接头地震力学特性研究[J]. 铁道学报, 2022, 44(2): 117 − 125. GENG Ping, GUO Xiangyu, WANG Qi, et al. Study on earthquake behavior characteristics of longitudinal joint of shield tunnel based on submodeling method [J]. Journal of the China Railway Society, 2022, 44(2): 117 − 125. (in Chinese)
[8] 何玉明, 龙渝川. 子模型在高层建筑薄弱部位分析中的适应性研究[J]. 工程建设, 2017, 49(10): 22 − 27. HE Yuming, LONG Yuchuan. Adaptability analysis of sub-model technique in the weak part of high-rise buildings [J]. Engineering Construction, 2017, 49(10): 22 − 27. (in Chinese)
[9] 关凯, 常晓林, 马刚. 基于动力子模型法的混凝土重力坝动力损伤分析[J]. 水电能源科学, 2013, 31(11): 65 − 69. GUAN Kai, CHANG Xiaolin, MA Gang. Dynamic damage analysis of concrete gravity dam based on dynamic submodel method [J]. Water Resources and Power, 2013, 31(11): 65 − 69. (in Chinese)
[10] ZHOU X Q, HAO H. Modelling of compressive behaviour of concrete-like materials at high strain rate [J]. International Journal of Solids and Structures, 2008, 45(17): 4648 − 4661. doi: 10.1016/j.ijsolstr.2008.04.002
[11] 徐磊, 崔姗姗, 姜磊, 等. 基于双重网格的混凝土自适应宏细观协同有限元分析方法[J]. 工程力学, 2022, 39(4): 197 − 208. doi: 10.6052/j.issn.1000-4750.2021.08.0610 XU Lei, CUI Shanshan, JIANG Lei, et al. Adaptive macro-meso-scale concurrent finite element analysis approach of concrete using dual mesh [J]. Engineering Mechanics, 2022, 39(4): 197 − 208. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.08.0610
[12] YIN Y J, REN Q W, SHEN L. Study on the effect of aggregate distribution on mechanical properties and damage cracks of concrete based on multifractal theory [J]. Construction and Building Materials, 2020, 262: 120086. doi: 10.1016/j.conbuildmat.2020.120086
[13] SHEN L, REN Q W, XIA N, et al. Mesoscopic numerical simulation of effective thermal conductivity of tensile cracked concrete [J]. Construction and Building Materials, 2015, 95: 467 − 475. doi: 10.1016/j.conbuildmat.2015.07.117
[14] 李健, 金浏, 余文轩, 等. 混凝土动态双轴压缩强度准则细观研究[J]. 工程力学, 2023, 40(11): 59 − 68. doi: 10.6052/j.issn.1000-4750.2022.01.0091 LI Jian, JIN Liu, YU Wenxuan, et al. Meso-simulation on dynamic biaxial compressive strength criterion of concrete [J]. Engineering Mechanics, 2023, 40(11): 59 − 68. (in Chinese) doi: 10.6052/j.issn.1000-4750.2022.01.0091
[15] LUBLINER J, OLIVER J, OLLER S, et al. A plastic-damage model for concrete [J]. International Journal of Solids and Structures, 1989, 25(3): 299 − 326. doi: 10.1016/0020-7683(89)90050-4
[16] LEE J, FENVES G L. Plastic-damage model for cyclic loading of concrete structures [J]. Journal of Engineering Mechanics, 1998, 124(8): 892 − 900. doi: 10.1061/(ASCE)0733-9399(1998)124:8(892)
[17] 徐海滨, 杜修力, 杨贞军. 基于预插黏性界面单元的Koyna重力坝强震破坏过程分析[J]. 振动与冲击, 2014, 33(17): 74 − 79, 84. XU Haibin, DU Xiuli, YANG Zhenjun. Seismic failure analysis of Koyna gravity dam using cohesive interface elements [J]. Journal of Vibration and Shock, 2014, 33(17): 74 − 79, 84. (in Chinese)
[18] National Research Council. Earthquake engineering for concrete dams: Design, performance, and research needs [M]. Washington: National Academy Press, 1990: 99 − 100.
[19] 王志远. 重力坝的实测坝踵应力及原因分析[J]. 大坝观测与土工测试, 2000, 24(6): 14 − 17. WANG Zhiyuan. Observed stresses in dam heel and analyses of causes [J]. Dam Observation and Geotechnical Tests, 2000, 24(6): 14 − 17. (in Chinese)
[20] 刘霞. 混凝土重力高坝坝踵开裂对坝体受力性能的影响研究[D]. 杨凌: 西北农林科技大学, 2008. LIU Xia. Study on effects of high concrete gravity dam mechanical properties due to cracking at dam hell [D]. Yangling: Northwest A&F University, 2008. (in Chinese)
[21] YIN Y J, REN Q W. Studying the representative volume of concrete using the entropy weight–grey correlation model [J]. Magazine of Concrete Research, 2018, 70(15): 757 − 769. doi: 10.1680/jmacr.17.00263
[22] BISCHOFF P H, PERRY S H. Compressive behaviour of concrete at high strain rates [J]. Materials and Structures, 1991, 24(6): 425 − 450. doi: 10.1007/BF02472016
[23] SNOZZI L, CABALLERO A, MOLINARI J F. Influence of the meso-structure in dynamic fracture simulation of concrete under tensile loading [J]. Cement and Concrete Research, 2011, 41(11): 1130 − 1142. doi: 10.1016/j.cemconres.2011.06.016
[24] 金浏, 杜修力. 加载速率及其突变对混凝土压缩破坏影响的数值研究[J]. 振动与冲击, 2014, 33(19): 187 − 193. JIN Liu, DU Xiuli. Effects of loading rate and its sudden change on concrete compressive failure [J]. Journal of Vibration and Shock, 2014, 33(19): 187 − 193. (in Chinese)
[25] JIN L, YU W X, DU X L, et al. Meso-scale modelling of the size effect on dynamic compressive failure of concrete under different strain rates [J]. International Journal of Impact Engineering, 2019, 125: 1 − 12. doi: 10.1016/j.ijimpeng.2018.10.011
[26] MC90 C. Comite Euro-International du Beton. CEB-FIP Model Code 1990 [J]. Bulletin D’Information, 1993, 42(215): 43 − 50.
[27] MALVAR L J, ROSS C A. Review of strain rate effects for concrete in tension [J]. ACI Materials Journal, 1998, 95(6): 735 − 739.
[28] GROTE D L, PARK S W, ZHOU M. Dynamic behavior of concrete at high strain rates and pressures: I. experimental characterization [J]. International Journal of Impact Engineering, 2001, 25(9): 869 − 886. doi: 10.1016/S0734-743X(01)00020-3
计量
- 文章访问数: 111
- HTML全文浏览量: 35
- PDF下载量: 38
