STUDY ON EXTREME VALUES AND NON-COLLINEAR CHARACTERISTICS OF WAVES AND CURRENT PARAMETERS IN A SEA STRAIT UNDER TYPHOONS
-
摘要:
强台风极端天气系统常在海峡区域引发强波流耦合作用，其中非共线波流作用产生的极端波对区域内桥梁等建筑设施构成巨大威胁。现有波、流作用研究普遍针对共线或正交的情况进行展开，很少针对实际情况进行研究，因此该文建立了波流耦合模型以探明台风作用下波、流及其波流夹角特性，通过对1987年−2018年期间51次台风进行数值模拟获取环境数据，构建波-流-波流夹角三维联合概率模型及波流环境等值线模型，对波、流要素极值和波流夹角进行讨论。研究表明：波高极值和流速极值对应时刻波流均呈现非共线特性，波高极值主要出现在波流反向情况，而流速极值多出现在波流同向情况；给定重现期下环境等值线的环境参数极值受环境参数选取时刻影响较大；极端情况下，波流夹角在0°~30°和150°~180°出现概率可达80%。
Abstract:Severe typhoons usually induce extreme wave and current coupled environments in sea strait areas, which poses a significant threat to structural safety of offshore structures, such as buildings and bridges. The focus of existing research has been mainly on the collinear wave-current scenarios, but less on the actual wave-current conditions in the strait. This paper addressed the issue by establishing a wave-current coupled metocean simulation model to investigate the characteristics of wave currents and their intersection angles in Qiongzhou Strait induced by historical typhoons. The environmental data were obtained by simulating 51 typhoons between 1987 and 2018. A three-dimensional joint probability model of wave height, current speed and the intersection angle and the associated environmental contour model were then constructed. The extreme values of wave and current parameters were finally investigated. The research reveals that extreme wave height and current speed in the strait exhibit non-collinear characteristics. In extreme scenarios, the probability of wave-current intersection angles between 0°-30° and 150°-180° can reach up to 80%. Extreme wave height predominantly occurs when the current and wave are in opposite directions, while extreme current speed appears when the wave and current propagate in the same direction. The extreme values of wave and current parameters depend on the extraction time for a given return period.
-
近些年来，我国桥梁事业蓬勃发展，技术手段和建设经验愈加丰富，使得桥梁建设不断向海洋区域延伸。2020年底国家颁布的《综合立体交通网规划纲要》提出加强跨海通道基础设施建设方案论证，将琼州海峡纳入国家综合立体交通网主骨架布局。台风作为常见的极端气候[1]，易在海峡区域中引起巨浪与急流，而与海湾、入海口等开阔海域不同，海峡区域地形变化剧烈，存在显著的海水“狭管效应” [2]，进一步增加了桥梁水动力作用的复杂性，这给桥梁建设带来了巨大的风险和技术挑战[3 − 4]。
波浪和海流是海峡通道内的主要水动力因素。开阔海域水面宽广，波浪主要由风产生，波高和风速存在显著的正相关性，海流则相对稳定而缓慢(流速<1 m/s)，一般呈现强波、弱流的情况。但当海流由开阔海域涌入海峡时，受“狭管效应”影响，过流断面急剧缩小，体积难以压缩的海水便会加速流出海峡。以琼州海峡为例，受“狭管效应”影响，最大平均流速可超过2.8 m/s[5]。强波和强流之间存在复杂的非线性耦合作用[6]，显著区别于强波、弱流情况。而台风经过海峡通道时的大风抽吸、夹卷效应，会进一步加强水体混合，使通道内波-流特性更加复杂[7]。目前学者围绕波-流耦合作用开展过大量试验和数值分析[8]，但多数研究仅考虑了波、流共线(同向或反向)的情况[9]。海峡中的海流方向相对固定，但波浪方向受强风环境影响大，常出现强波、强流非共线(斜交)的情况。波浪与海流的斜交会使长峰波演变成短峰波，甚至出现极端波，严重威胁工程安全[10]。海洋工程结构多采用圆柱截面，最不利荷载出现在波、流共线时，然而，桥墩截面形状复杂多样，水动力荷载对波、流方向及夹角十分敏感[11]，仅考虑共线波-流作用无法有效支撑结构设计。因此，为给桥梁波-流空间作用研究提供参考依据，有必要对“狭管效应”下的强波、强流耦合场开展波、流及波流夹角特性研究。
基于历史观测数据对风、浪、流等环境变量开展环境特性研究是常用研究手段，但由于实际野外测量环境恶劣，受限较多，弊端明显，观测得到的数据并不能满足目前需求。近年来，数值模拟技术快速发展，台风作用下极端环境数值模拟为诸多学者广泛使用。李庆杰等[12]基于FVCOM对北海区域风暴潮进行模拟，效果良好。魏凯等[13]基于ADCIRC(Simulating Waves Nearshore) +SWAN (An Advanced Circulation Model For Oceanic, Coastal and Estuarine Waters)进行台风作用下浪潮数值模拟，构建风-浪-潮环境等值面，与实测数据对比精度优良，说明数值模拟能较好模拟波浪等环境。
以琼州海峡为例，通过ADCIRC+SWAN波流耦合模式构建数值模型，对1987年−2018年经过研究区域的51条历史台风进行数值模拟，获取波、流等环境数据。基于模拟所得环境数据获取波流在海峡区域的分布特性；采用Copula函数构建波-流-波流夹角三维联合概率模型，对波流夹角特性进行分析，并基于IFORM方法构建给定重现期下的波流环境等值线、讨论波、流极值(文中所有关于波、流方向的定义均为：东向为波向和流向的0°方向，逆时针为正方向，波流夹角为波向与流向的数值差值)。
1 台风作用下浪-流数学模型
1.1 风场模型
风场由移行风场加梯度风场组合形式，表达式为：
v=vm+vgs (1) 式中：vm为移行风场；vgs为海面高度处的梯度风场。移行风场采用UENO[14]提出的经验公式进行计算，表达式为：
vm(r)=vmcexp(−π4|r−Rm|Rm) (2) 式中：r为计算点位到台风中心的距离；vmc为台风中心移动速度；Rm为台风最大风速半径。选用应用广泛且对区域适用性较好的HOLLAND[15]气压模型描述台风的剖面气压，通过对边界层空气质点的气压梯度力、离心力和科氏力进行平衡求解获取梯度风速vg，其表达式为：
p(r)=pc+(pn−pc)e−(Rmr)B (3) vg(r)=√Bρa(Rmr)BΔpe−(Rmr)B+(rf2)2−rf2 (4) 式中：p(r)为距离台风中心距离为r处的气压；pc为台风中心气压；pn为台风外围气压； ρa(取值1.29 kg/m3)为空气密度；f为科氏力参数，f=2ωsinφ，其中ω(取值7.292×10−5 rad/s)为地球自转角速度，φ为纬度； B为台风剖面气压形状参数。采用李瑞龙[16]拟合的经验公式计算Rm， 采用HOLLAND[15]提出的经验公式对B进行计算，表达式为：
Rm=exp(−0.163(1013−pc)0.555+5.212) (5) B=2−pc−900160 (6) 根据HARPER等[17]提出的经验公式将梯度风速由大气边界层转换到计算海面高度处，公式具体为：
vgs(r)=Km⋅vg(r) (7) 式中：Km为风速转化因子，其计算表达式为：
Km={0.81,vg<6m/s0.81−0.00296(vg−6),6<vg<19.50.77−0.00431(vg−19.5),19.5<vg<450.66,vg>45m/s (8) 将获取的梯度风场和移行风场，考虑流入角(本文取值20°[18])进行叠加得到参数风场。PAN等[19]提出参数风场中心精度高，外围精度低，为更精确模拟台风风场，采用 CCMP再分析风场与参数风场进行再叠加获取精度更为良好的混合风场，表达式为：
{vH=vpara,r⩽ (9) 式中： {v_{{\mathrm{para}}}} 为参数风场； {v_{{\mathrm{ccmp}}}} 为再分析风场。
\alpha = \frac{{r - {R_1}}}{{{R_2} - {R_1}}} (10) 式中：R1取300 km；R2取450 km。
1.2 ADCIRC + SWAN波流耦合模式
耦合模式中ADCIRC和SWAN采用同一个非结构网格，模式的具体的工作流程可见图1。步骤为：1) SWAN模型利用输入的数据对波浪进行计算，并将计算得到的波浪辐射应力梯度传递给ADCIRC模型；2) ADCIRC根据接收到的台风数据、波浪辐射应力和潮位参数对水位和水流进行计算；3)在ADCIRC完成计算后，SWAN接收新的水位和水流信息；4) SWAN根据信息开始进行下步耦合计算，并将计算的波浪辐射应力传给ADCIRC，与ADCIRC结合重复进行步骤2)~步骤4)，重复循环，最终完成计算，输出分析所需要的波高和流速等数据。
![]()
图 1 波流耦合数值模拟框架Figure 1. The framework of numerical simulation for wave-current interaction2 模型验证和历史台风模拟
2.1 算例数值模型
根据文献[20]，选取琼州海峡跨海通道中线方案为中心建立中尺度的海域数值模型，大致范围为：105°E~116°E，15°N~23°N，包含雷州半岛、海南省等，如图2所示。表1中给出包括中线在内，目前推荐的3种跨海通道路径方案。模型采用非结构化三角形网格，外海区域采用大尺寸，仅对研究区域进行细化，从而提高计算效率和准确性。工程海域附近网格尺寸最小为40 m，外海最大网格尺寸为27 km，网格数为100 077，节点数为51 891。边界水位采用TPXO9_atlas模型的模块组合：K1、K2、M2、N2、O1、P1、Q1、S2模拟获取。
表 1 跨海通道线路方案Table 1. Sea-cross channel route scheme编号 线路 长度/km 最大水深/m 西线 雷州灯楼角-海南红牌咀 31.8 40 中线 雷州三塘-海南天尾角 20.3 88 东线 雷州排尾角-海南白沙角 19.7 86 2.2 模型验证
为验证模型的准确性，在建模区域选取测量潮汐的海安站对潮汐进行验证，并选取1213号台风“启德”过境期间风速测量塔及浮标测量的环境数据对有效波高及风速等进行验证。
混合风场的准确性通过对1213号台风“启德”期间风速进行模拟验证。1213号台风模拟时间为2012年8月15日6时—2012年8月18日6时，以风塔实测[21]风速和风向对比进行验证，如图3所示。合成风场与台风期间实测风速和风向整体吻合较好。
为验证TPXO模型对水位预测的准确性，对2014年9月13日0时—2014年9月19日0时进行潮汐模拟，以海岸站实测数据对比验证，如图4所示，数据吻合度较高，说明TPXO潮汐模型能较好预测边界水位。
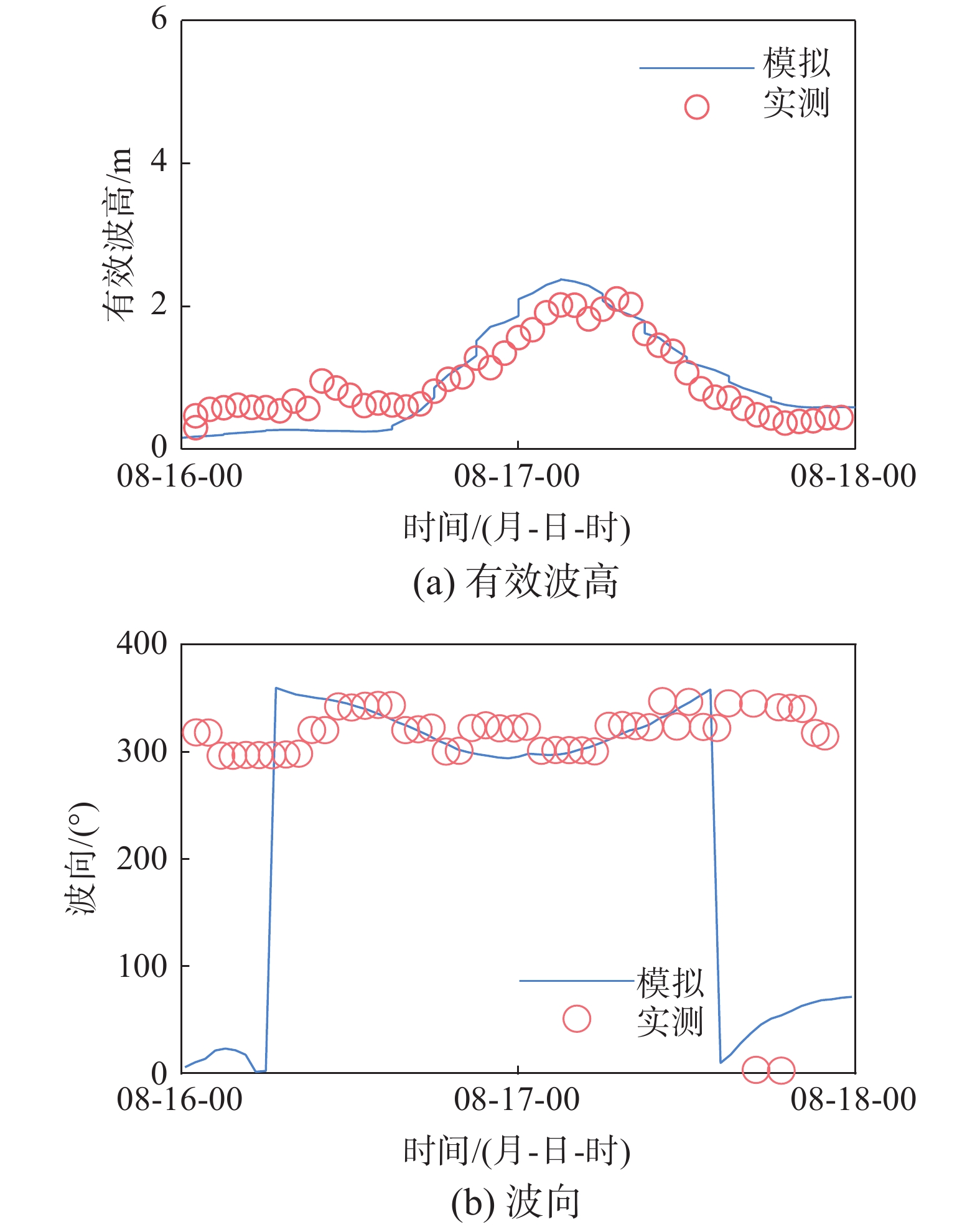
为验证SWAN+ADCIRC模式对波浪及海流模拟的准确性，对1213号台风“启德”进行数值模拟，模拟时间段分为：2012年8月15日6时—2012年8月18日6时，时长均为3 d，以浮标实测数据[21]进行对比验证，如图5~图6。实测最大有效波高2.26 m，模拟最大有效波高为2.47 m，相对误差为9.3%；实测最大流速为0.91 m/s，模拟最大流速为0.94 m/s，相对误差为3.3%。数值模拟波向和流向与实测吻合整体良好，说明模型能较好模拟琼州海峡区域海浪和海流。
2.3 历史台风数值模拟
据中国气象局统计，1987年—2020年西北太平洋有700多个历史热带气旋。参考YIN等[22]研究中提出的涉及的台风选取方法，以琼州海峡区域海口作为中心点(下文以CRP代称)，基于台风中心气压(pc/hPa)和风暴中心到CRP的距离(D/km)对历史台风进行选取：
1) CRP到历史台风路径最近距离不大于500 km。
2) 历史台风中心气压不大于980 hPa。
最终选取51条历史台风，路径如图7所示。
2.4 台风作用下海峡通道波、流要素极值
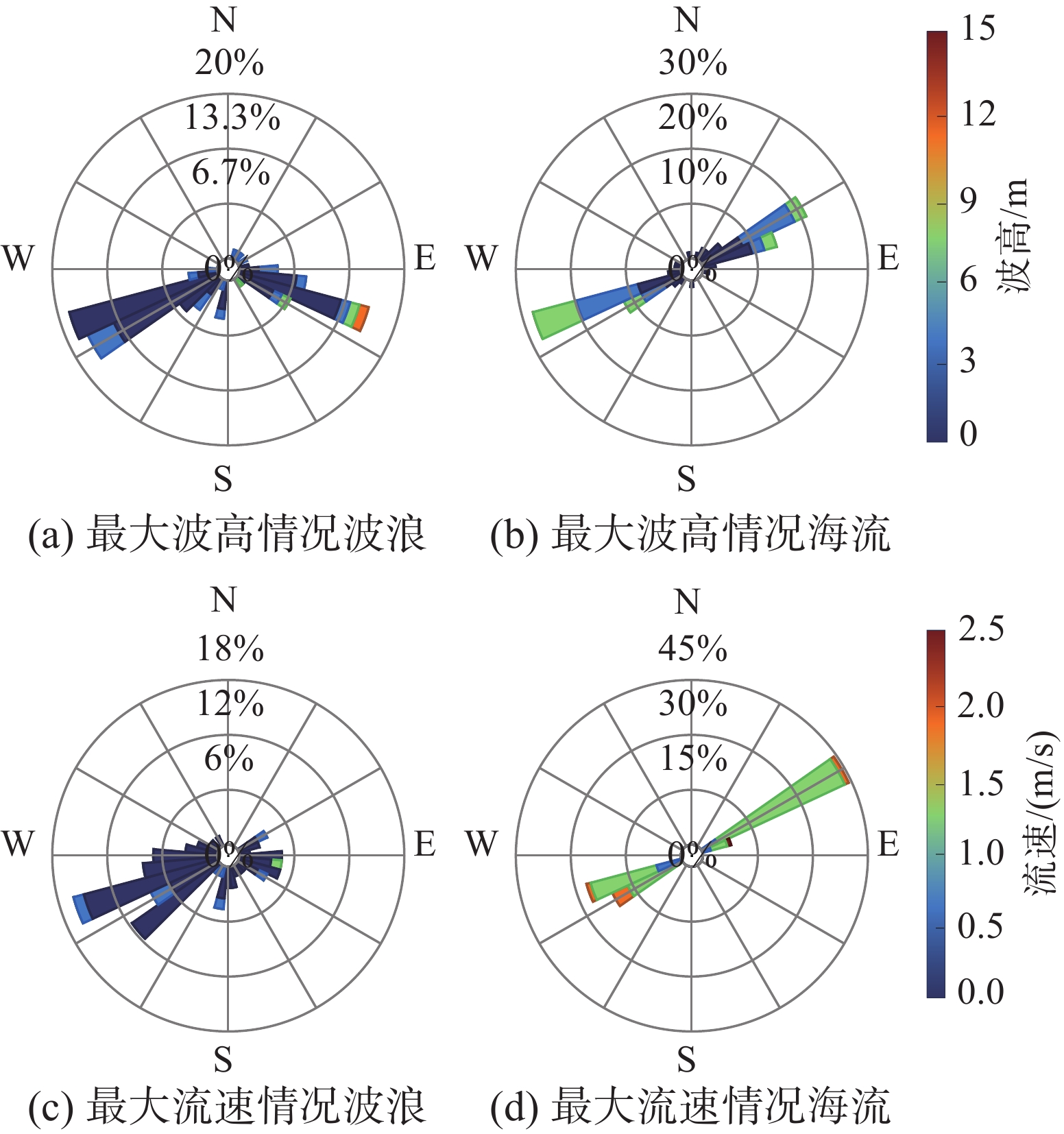
图8展示了51次历史台风作用下琼州海峡区域最大有效波高分布、最大流速分布及其对应波流夹角分布。51次台风作用下其中波高和流速在海峡中部和右端大，而左端较小，这可能是由于海南岛的遮蔽效应引起的。最大波高时刻波流夹角在海峡中部为大夹角两端为小夹角，对比图8(a)和图8(c)，大夹角位置对应波高均较大。最大流速时刻波流夹角在海峡中呈现从右向左变大的分布，且在流速较大部分，夹角均较小。
![]()
图 8 琼州海峡最大波高、流速及对应时刻波流夹角分布Figure 8. Maximum wave height, flow velocity and wave-current angle distribution at corresponding time in Qiongzhou Strait根据51次台风模拟结果选取跨海通道中线附近波高最大点P1和流速最大点位P2为研究点位，以51次台风作用下，每次台风作用期间研究点位对应的环境参数构建三个数据集，如表2所示。三个数据集均值及标准差如表3所示。数据集一的最大波高、最大流速、最大波高时刻波流夹角、最大流速时刻波流夹角分别为11.078 m、1.472 m/s、129.149°、2.905°；数据集二的最大波高、最大流速、最大波高时刻波流夹角、最大流速时刻波流夹角分别为7.36 m、2.028 m/s、35.832°、35.832°。数据集一的流速和数据集二的波高与数据集三相比明显偏小，说明最大波高和最大流速之间相关性较弱，数据集二最大波高和最大流速同时出现，说明流速增大能改善波流之间的相关性。
表 2 环境参数工况数据集Table 2. Environmental parameters working condition data set工况 波高选取 流速选取 波流夹角选取 数据集一 最大波高 对应时刻流速 对应时刻波流夹角 数据集二 对应时刻波高 最大流速 对应时刻波流夹角 数据集三 最大波高 最大流速 波高时刻波流夹角 表 3 工况数据集环境参数均值及标准差Table 3. Mean and standard deviation of environmental parameters in working condition data set工况 波高/m 流速/(m·s−1) 波流夹角/(°) 均值 标准差 均值 标准差 均值 标准差 数据集一 2.721 1.571 0.549 0.401 84.166 62.969 数据集二 1.464 1.181 1.197 0.197 65.368 61.177 数据集三 2.721 1.571 1.197 0.197 84.166 62.969 从图9中可以看出台风作用期间，海流方向比较固定，存在主流向，方向与海峡管道方向相关性强，说明地形对海流方向影响较大，台风作用期间强风环境对海流方向影响较小。波方向变化区间大，方向不稳定，反映波方向受台风期间强风环境影响较大，说明琼州海峡区域台风作用下，波流夹角主要由波方向控制。下面通过构建波-流-波流夹角联合概率分布基于波流夹角讨论波流非共线特性。
![]()
图 9 研究点位波向及流向分布Figure 9. Direction of wave and flow distribution at the research point3 波-流-波流夹角联合概率模型及波-流环境等值线
3.1 多维联合概率模型
Copula是基于SKLAR[23]定理构建的能将多变量的联合分布函数或其边缘分布进行连接的工具。假定变量 {x_1} ， {x_2} ， {x_3} ， \ldots ， {x_n} 的边缘概率分布函数为 {F_1}({x_1}) ， {F_2}({x_2}) ， {F_3}({x_3}) ， \ldots ， {F_n}({x_n}) ，若边缘分布函数 {F_1} ， {F_2} ， {F_3} ， \ldots ， {F_n} 均连续，则存在唯一的Copula连接函数C满足式(10) [24]。采用双层嵌套的方式构建波-流-波流夹角联合概率分布，见式(11)，具体建模步骤如下：
1) 建立海流、波高和波流夹角的边缘概率分布。
2) 通过Copula函数将环境变量进行两两连接。
3) 根据拟合精度和环境变量之间的相关性选择第一层连接的环境变量，选取准则为：
a) 选取与其它变量相关性均较强
b) 拟合精度以RMSE和卡方检验作为判定指标。其中RMSE计算如下：
{\mathrm{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left[ {{p_{{\mathrm{si}}}}(i) - {p_{{\mathrm{ex}}}}(i)} \right]}^2}} } (11) 式中： {p_{{\mathrm{si}}}} 为拟合概率分布理论值； {p_{{\mathrm{ex}}}} 为经验概率分布经验值。
4) 将构建好的二维联合概率分布 {C_{12}} 与最后一个变量的边缘概率分布利用Copula函数进行连接，形成波-流-波流夹角联合分布 {C_{123}} 。
F({x_1},{x_2}, \ldots ,{x_n}) = C({F_1}({x_1}),{F_2}({x_2}), \ldots ,{F_n}({x_n})) (12) {{{C}}_{123}}( {{x_1},{x_2},{x_3};{\theta _1},{\theta _2}} ) = C( {{F_3},{C_{12}}( {{F_1},{F_2};{\theta _1}} );{\theta _2}} ) (13) 式中， {\theta _i} 为相关性系数。波-流-波流夹角的联合概率密度分布f123(x1, x2, x3)表达式为：
{f_{123}}({x_1},{x_2},{x_3}) = {c_{123}} \cdot {f_1}({x_1}) \cdot {f_2}({x_2}) \cdot {f_3}({x_3}) (14) 式中， {c_{123}} 可由式(15)求得，具体形式为：
{c_{123}} = \frac{{\partial {C_{123}}({F_1}({x_1}),{F_2}({x_2}),{F_3}({x_3}))}}{{\partial {F_1}({x_1})\partial {F_2}({x_2})\partial {F_3}({x_3})}} (15) 3.2 环境变量边缘分布构建
采用广义极值分布(GEV)对最大有效波高(下面以Hm表示，其对应情况下流速以Ch表示)及最大流速(下面以Cm表示，其对应情况下有效波高以Hc表示)两种情况下波、流环境参数进行拟合，拟合参数及检验见表3，采用GEV能较好地拟合波高和流速的边缘分布。
GEV分布函数如下：
F(x) = \left\{ \begin{aligned} & \exp \left[ { - {{\left( {1 + k\frac{{x - \mu }}{\sigma }} \right)}^{ - \tfrac{1}{k}}}} \right] ,\;\;{k \ne 0} \\ & \exp \left[ { - \exp \left( { - k\frac{{x - \mu }}{\sigma }} \right)} \right] ,\;\;{k = 0} \end{aligned} \right. (16) 式中， \sigma 、 \mu 、 k 分别为尺度、位置和形状参数。
波流夹角具有明确上下界限，应该采用有界的分布形式对其分布规律进行描绘，本节对王涛等[25]提出的有界概率分布(LPD)模型进行变化，建立琼州海峡的波流夹角的边缘分布。表达式如下：
F(x;a,b,\alpha ,\beta ) = \exp \left[ { - \frac{{{{(b - x)}^\beta }}}{{{{(x - a)}^\alpha }}}} \right],\;a {\leqslant} x {\leqslant} b (17) 式中：a、b为x取值的下界和上界； \alpha 、 \beta 为待定系数。当x=a时， F = 0 ；当x=b时， F = 1 。有界概率分布模型的概率密度表达为：
\begin{split} & f(x;a,b,\alpha ,\beta ) = \exp \left[ { - \frac{{{{(b - x)}^\beta }}}{{{{(x - a)}^\alpha }}}} \right] \cdot \\&\qquad \left( {\beta \frac{{{{(b - x)}^{\beta - 1}}}}{{{{(x - a)}^\alpha }}} + \alpha \frac{{{{(b - x)}^\beta }}}{{{{(x - a)}^{\alpha + 1}}}}} \right),\;a {\leqslant} x {\leqslant} b \end{split} (18) 采用最小二乘法对有界概率分布函数中的参数进行获取，拟合结果及检验见表4可以看出有界概率分布能较好拟合波流夹角的边缘分布。
表 4 边缘分布信息Table 4. Marginal distribution information变量 方法 形状
参数k位置参数 \mu /
待定系数 \beta尺度参数 \sigma /
待定系数 \alpha均方根差
RMSEK-S检验 Hm GEV 0.1658 2.0348 0.8761 0.0259 通过 Ch GEV 0.0041 0.3516 0.2888 0.0478 Ah LPD − 0.4210 0.5637 0.0412 Hc GEV 0.1933 0.9075 0.6917 0.0259 通过 Cm GEV −0.0848 1.1140 0.1713 0.0334 Ac LPD − 0.3538 0.5785 0.0340 3.3 波-流-波流夹角联合概率分布
获得边缘分布后，通过Copula函数进行连接。采用Kendall相关系数法对波高、流速和夹角进行相关性分析，Tau绝对值越大相关性越强。选取水文中常用的Frank Copula函数对波高、流速、波流夹角进行连接，见式(18)，拟合结果及检验见表5。
{{C}}(u,v;\theta ) = - \frac{1}{\theta }\ln \left( {1 + \frac{{({{\mathrm{e}}^{ - \theta u}} - 1)({{\mathrm{e}}^{ - \theta v}} - 1)}}{{{{\mathrm{e}}^{ - \theta }} - 1}}} \right) (19) 式中：u、v分别为边缘分布函数F(x1)、F(x2)；θ为Copula函数的相关性参数。
表 5 二维Fank Copula 联合分布相关参数Table 5. Fitted parameters of Frank Copula工况 组合 Kendall系数
TauCopula参数
θ均方根差
RMSE数据集一 Hm-Ch 0.0566 0.3656 0.0451 Hm-Ah −0.1070 −0.6672 0.0396 Ch-Ah −0.0867 −0.6644 0.0505 数据集二 Hc-Cm 0.3609 3.7960 0.0401 Hc-Ac −0.3012 −3.1162 0.0290 Cm-Ac −0.1321 −1.1227 0.0394 数据集三 Hm-Cm 0.3445 3.6783 0.0347 Hm-Ah −0.1070 −0.6672 0.0396 Cm-Ah −0.2120 −1.6406 0.0429 变量组合“波高-流速”、“波高-波流向夹角”、“流速-波流向夹角”分别呈正相关、负相关、负相关，在流速较大的情况下变量之间的相关性存在不同程度的加强，说明海流对波浪存在明显的影响。由于波高与其它变量综合相关性最强，以相关性强的波-流作为双层嵌套的第一层。
三个数据集的波-流-波流夹角联合概率分布拟合的RMSE分别为0.0361、0.0316、0.0450，决策系数R2分别为0.9554、0.9463、0.9611，精度良好，表明双层嵌套Frank Copula能较好的拟合波-流-波流夹角联合概率分布。
3.4 多重现期下波-流环境等值线
基于Copula函数构建的波流联合概率分布，采用逆一阶可靠度方法(IFORM)[26]构建三个数据集对应的波-流环境等值线，见图10。图10中给出重现期2年、5年、10年、50年和100年下的等值线，最大波高参数对应流速和最大流速参数对应波高随重现期变化较小。表6给出重现期50年和100年下，三大数据集最大波浪和最大流速环境参数，数据集一最大波高和数据集二最大流速与数据集三几乎相同，后续仅对比数据集一和数据集二最大环境参数。数据集一100年重现期对比50年重现期下最大环境参数，最大波高增加17.9%，最大流速增加13.1%；数据集二100年重现期对比50年重现期下最大环境参数，最大波高增加22.2%，最大流速增加5%，可以看出相比最大波高情况，在极值流速情况下，其对应的最大环境参数中波高增幅要远大于流速增幅。50年重现期下数据集一最大波高比数据集二大36.5%，最大流速比数据集二小9.4%；100年重现期下数据集一最大波高比数据集二大31.6%，最大流速比数据集二小2.5%，说明流速受参数选取时刻影响较小，波高受参数选取时刻影响较大，若结构对波高较敏感，采用最大流速时刻的数据获取的设计参数，结构偏于危险。
表 6 50年和100年重现期下环境等值线最大环境参数Table 6 The maximum environmental parameters of isoline under 50-year and 100-year return periods重现期/年 最大环境参数 数据集一 数据集二 数据集三 50 最大波高/m 7.393 5.418 7.384 最大流速/(m·s−1) 1.579 1.744 1.741 100 最大波高/m 8.715 6.620 8.722 最大流速/(m·s−1) 1.785 1.831 1.825 3.5 波、流极值情况非共线特性
基于三个数据集，构建对应的联合概率密度分布，其切片图见图11，三大数据集波流夹角从0°~180°整体上呈现先减小后增大的趋势，数据集一和数据集三波流夹角从2°~20°出现概率增加，而数据集二波流夹角从2°~20°出现概率减小。波流夹角90°时概率密度值均最小，说明极端波流情况下，波流夹角为正交的情况概率最低。从分布形状上看，最大波高情况下，随着波流夹角增大等值线形状几乎没有变化，而最大流速和波流均为极值情况下，随着波流夹角增大等值线形状由椭圆向对称三角形变化，数据整体离散性变小，相关性增强，这与表5的计算结果相对应。邹志利[27]在文章中提到弱流对波浪影响较小，强流情况下波流作用加剧，上述现象一定程度上是由此引起的。
![]()
图 11 波-流-波流夹角三维联合概率密度切片分布(切点：2°、20°、45°、70°、90°、120°、145°、160°、179°)Figure 11. Three-dimensional joint probability density slice distribution of wave-current-included angle of wave-current (tangent point : 2 °, 20 °, 45 °, 70 °, 90 °, 120 °, 145 °, 160 °, 179 °)图12给出波-流-波流夹角联合概率分布中波流夹角分布情况，以10°为间隔进行累积概率分布计算给出折线及柱状图。三种情况下0°~10°、10°~20°、20°~30°、30°~40°、40°~170°、170°~180°和150°~180°对应波流夹角的累计概率分布值见表7。最大波高情况下波流夹角0°~30°出现概率比最大流速情况下对应角度出现概率低了43.3%，波流夹角150°~180出现概率比最大流速情况下对应角度出现概率高了39.7%，最大波高情况下波流夹角倾向于大角度，最大流速情况相反，与2.3节中分析结果相同。
![]()
图 12 波流夹角10°间隔概率分布Figure 12. The probability distribution of wave-current angle 10 ° interval表 7 考虑相关性下波流夹角对应区域间累积概率Table 7. The cumulative probability of the interval corresponding to the angle considering the correlation波流夹角区间 数据集一
累积概率数据集二
累积概率数据集三
累积概率0°~10° 0.109 0.318 0.111 10°~20° 0.140 0.189 0.142 20°~30° 0.084 0.082 0.085 30°~40° 0.054 0.045 0.054 40°~170° 0.227 0.126 0.226 170°~180° 0.386 0.240 0.382 150°~180° 0.429 0.258 0.424 4 结论
本文采用 Holland 模型结合UENO模型构建参数风场并与CCMP再分析风场叠加形成混合风场，通过SWAN+ADCIRC 波流耦合模式，模拟了台风作用下琼州海峡区域波浪等环境参数，结合风、浪实测资料对数值模拟结果进行了验证。对历史台风进行选取并对浪流进行分析得出的主要结论如下：
(1)构建的数值模型能较好模拟台风作用期间琼州海峡区域波浪等海洋环境的发展，为研究提供环境变量数据集。
(2) 台风作用下，琼州海峡区域最大波高呈现中部和东部大、西部小的分布，对应时刻波流夹角在波高较大区域为大数值。最大流速呈现从东向西降低的分布，对应时刻波流夹角呈中部和东部小、西部大的分布。
(3)台风期间波高和流速的边缘分布通过GEV拟合效果较好，波流夹角的边缘分布可以通过LPD拟合获取，精度较高。采用双层Frank Copula能较好构建波-流-波流夹角三维联合概率分布，反映其分布特征。
(4)琼州海峡区域给定重现期下环境等值线的波、流要素中流速受环境参数选取时刻影响较小，波高受环境参数选取时刻影响较大。
(5)最大波高情况下波流夹角0°~20°出现概率逐渐增大，20°~180°先减小后增大；最大波高情况下波流夹角0°~180°出现概率先减小后增大。最大波高情况下波流夹角0°~30°出现概率为33.4%，比最大流速情况下对应角度出现概率低了43.3%，波流夹角150°~180°出现概率为42.9%，比最大流速情况下对应角度出现概率高了39.7%，最大波高情况下波流夹角倾向于大角度，最大流速情况相反。
综上，本文模型模拟精度较好，能有效地用于模拟台风作用下近岸海域的极端风、浪等环境，可为开展风-浪-流环境荷载概率分析，提供数据来源。但是实际台风结构往往是不对称的，采用对称的Holland 气压模型，对不对称的台风结构进行描述，本身就是一种近似。同时，限于篇幅本文未对不同波流夹角下的海流和波浪如何相互影响进行探究，未来可开展台风作用期间波流耦合场时空演变对波流相互作用进行进一步探明。
-
![]()
图 1 波流耦合数值模拟框架
Figure 1. The framework of numerical simulation for wave-current interaction
![]()
图 8 琼州海峡最大波高、流速及对应时刻波流夹角分布
Figure 8. Maximum wave height, flow velocity and wave-current angle distribution at corresponding time in Qiongzhou Strait
![]()
图 9 研究点位波向及流向分布
Figure 9. Direction of wave and flow distribution at the research point
![]()
图 11 波-流-波流夹角三维联合概率密度切片分布(切点：2°、20°、45°、70°、90°、120°、145°、160°、179°)
Figure 11. Three-dimensional joint probability density slice distribution of wave-current-included angle of wave-current (tangent point : 2 °, 20 °, 45 °, 70 °, 90 °, 120 °, 145 °, 160 °, 179 °)
![]()
图 12 波流夹角10°间隔概率分布
Figure 12. The probability distribution of wave-current angle 10 ° interval
表 1 跨海通道线路方案
Table 1 Sea-cross channel route scheme
编号 线路 长度/km 最大水深/m 西线 雷州灯楼角-海南红牌咀 31.8 40 中线 雷州三塘-海南天尾角 20.3 88 东线 雷州排尾角-海南白沙角 19.7 86 
下载: 导出CSV
表 2 环境参数工况数据集
Table 2 Environmental parameters working condition data set
工况 波高选取 流速选取 波流夹角选取 数据集一 最大波高 对应时刻流速 对应时刻波流夹角 数据集二 对应时刻波高 最大流速 对应时刻波流夹角 数据集三 最大波高 最大流速 波高时刻波流夹角
下载: 导出CSV
表 3 工况数据集环境参数均值及标准差
Table 3 Mean and standard deviation of environmental parameters in working condition data set
工况 波高/m 流速/(m·s−1) 波流夹角/(°) 均值 标准差 均值 标准差 均值 标准差 数据集一 2.721 1.571 0.549 0.401 84.166 62.969 数据集二 1.464 1.181 1.197 0.197 65.368 61.177 数据集三 2.721 1.571 1.197 0.197 84.166 62.969
下载: 导出CSV
表 4 边缘分布信息
Table 4 Marginal distribution information
变量 方法 形状
参数k位置参数 \mu /
待定系数 \beta尺度参数 \sigma /
待定系数 \alpha均方根差
RMSEK-S检验 Hm GEV 0.1658 2.0348 0.8761 0.0259 通过 Ch GEV 0.0041 0.3516 0.2888 0.0478 Ah LPD − 0.4210 0.5637 0.0412 Hc GEV 0.1933 0.9075 0.6917 0.0259 通过 Cm GEV −0.0848 1.1140 0.1713 0.0334 Ac LPD − 0.3538 0.5785 0.0340
下载: 导出CSV
表 5 二维Fank Copula 联合分布相关参数
Table 5 Fitted parameters of Frank Copula
工况 组合 Kendall系数
TauCopula参数
θ均方根差
RMSE数据集一 Hm-Ch 0.0566 0.3656 0.0451 Hm-Ah −0.1070 −0.6672 0.0396 Ch-Ah −0.0867 −0.6644 0.0505 数据集二 Hc-Cm 0.3609 3.7960 0.0401 Hc-Ac −0.3012 −3.1162 0.0290 Cm-Ac −0.1321 −1.1227 0.0394 数据集三 Hm-Cm 0.3445 3.6783 0.0347 Hm-Ah −0.1070 −0.6672 0.0396 Cm-Ah −0.2120 −1.6406 0.0429
下载: 导出CSV
表 6 50年和100年重现期下环境等值线最大环境参数Table 6 The maximum environmental parameters of isoline under 50-year and 100-year return periods
重现期/年 最大环境参数 数据集一 数据集二 数据集三 50 最大波高/m 7.393 5.418 7.384 最大流速/(m·s−1) 1.579 1.744 1.741 100 最大波高/m 8.715 6.620 8.722 最大流速/(m·s−1) 1.785 1.831 1.825
下载: 导出CSV
表 7 考虑相关性下波流夹角对应区域间累积概率
Table 7 The cumulative probability of the interval corresponding to the angle considering the correlation
波流夹角区间 数据集一
累积概率数据集二
累积概率数据集三
累积概率0°~10° 0.109 0.318 0.111 10°~20° 0.140 0.189 0.142 20°~30° 0.084 0.082 0.085 30°~40° 0.054 0.045 0.054 40°~170° 0.227 0.126 0.226 170°~180° 0.386 0.240 0.382 150°~180° 0.429 0.258 0.424
下载: 导出CSV
-
[1] ZHONG X, WEI K, SHANG D M. An improved azimuth-dependent Holland model for typhoons along the Zhejiang coast prior to landfall based on WRF-ARW simulations [J]. Natural Hazards, 2023, 117(3): 2325 − 2346. doi: 10.1007/s11069-023-05944-9
[2] WHITEHEAD J A. Topographic control of oceanic flows in deep passages and straits [J]. Reviews of geophysics, 1998, 36(3): 423 − 440. doi: 10.1029/98RG01014
[3] WEI K, SHANG D M, ZHONG X. Life-cycle thinking-based decision support framework for multispan simply supported bridges under typhoon-induced wave, current and surge conditions [J]. Ocean Engineering, 2023, 288: 115965. doi: 10.1016/j.oceaneng.2023.115965
[4] 郭健, 钟陈杰, 王仁贵, 等. 跨海桥梁受台风影响的风速概率模型分析[J]. 工程力学, 2022, 39(增刊1): 180 − 186. doi: 10.6052/j.issn.1000-4750.2021.06.S035 GUO Jian, ZHONG Chenjie, WANG Rengui, et al. Analysis of wind speed probability model of sea-crossing bridge affected by typhoons [J]. Engineering Mechanics, 2022, 39(Suppl 1): 180 − 186. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.06.S035
[5] BAI P, LING Z, LIU C, et al. Effects of tidal currents on winter wind waves in the Qiongzhou Strait: A numerical study [J]. Acta Oceanologica Sinica, 2020, 39(11): 33 − 43. doi: 10.1007/s13131-020-1673-2
[6] 孟凡昌. 强海况下的波流相互作用研究[D]. 北京: 国家海洋环境预报中心, 2017. MENG Fanchang. Study on wave-current interaction under strong sea conditions [D]. Beijing: National Marine Environmental Prediction Center, 2017. (in Chinese)
[7] GUO A X, FANG Q H, LI H. Analytical solution of hurricane wave forces acting on submerged bridge decks [J]. Ocean Engineering, 2015, 108: 519 − 528. doi: 10.1016/j.oceaneng.2015.08.018
[8] WEI C X, ZHOU D C, OU J P. Wave and wave-current actions on a bridge tower: An experimental study [J]. Advances in Structural Engineering, 2019, 22(6): 1467 − 1478. doi: 10.1177/1369433218816523
[9] 刘桦, 王本龙, 薛雷平, 等. 桩基承台结构的波流力研究进展[J]. 应用数学和力学, 2013, 34(10): 1098 − 1109. doi: 10.3879/j.issn.1000-0887.2013.10.010 LIU Hua, WANG Benlong, XUE Leiping, et al. Recent progress in wave-current loads on foundation structure with piles and cap [J]. Applied Mathematics and Mechanics, 2013, 34(10): 1098 − 1109. (in Chinese) doi: 10.3879/j.issn.1000-0887.2013.10.010
[10] 康啊真, 殷瑞涛, 祝兵, 等. 基于 LES 的跨海桥梁施工期围堰波流力数值模拟[J]. 西南交通大学学报, 2020, 55(3): 537 − 544, 587. doi: 10.3969/j.issn.0258-2724.20180222 KANG Azhen, YIN Ruitao, ZHU Bing, et al. Numerical simulation of wave-current forces acting on cofferdam for sea-crossing bridge based on large eddy simulation [J]. Journal of Southwest Jiaotong University, 2020, 55(3): 537 − 544, 587. (in Chinese) doi: 10.3969/j.issn.0258-2724.20180222
[11] WANG Piguang, ZHAO Mi, DU Xiuli. Short-crested wave-current forces on composite bucket foundation for an offshore wind turbine [J]. Mathematical Problems in Engineering, 2019, 2019: 5932742.
[12] 李庆杰, 洪新, 曹雪峰, 等. 不同风应力拖曳系数对北海区台风风暴潮模拟精度的影响[J]. 海南热带海洋学院学报, 2023, 30(2): 92 − 100. LI Qingjie, HONG Xin, CAO Xuefeng, et al. Effects of different wind stress drag coefficients on simulation accuracy of typhoon storm surge in Beihai region [J]. Journal of Hainan Tropical Ocean University, 2023, 30(2): 92 − 100. (in Chinese)
[13] 魏凯, 钟茜, 沈忠辉, 等. 台风作用下风-浪-潮三维环境等值面模型[J]. 工程力学, 2021, 38(11): 189 − 198. doi: 10.6052/j.issn.1000-4750.2020.11.0831 WEI Kai, ZHONG Xi, SHEN Zhonghui, et al. Environmental contour of wind-wave-storm surges induced by typhoons [J]. Engineering Mechanics, 2021, 38(11): 189 − 198. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.11.0831
[14] UENO T. Numerical computations of the storm surges in Tosa Bay [J]. Journal of the Oceanographical Society of Japan, 1981, 37(2): 61 − 73. doi: 10.1007/BF02072559
[15] HOLLAND G J. An analytic model of the wind and pressure profiles in hurricanes [J]. Monthly Weather Review, 1980, 108(8): 1212 − 1218. doi: 10.1175/1520-0493(1980)108<1212:AAMOTW>2.0.CO;2
[16] 李瑞龙. 基于改进的台风关键参数的台风极值风速预测[D]. 哈尔滨: 哈尔滨工业大学, 2007. LI Ruilong. Prediction of typhoon extreme wind speeds based on improved typhoon key parameters [D]. Harbin: Harbin Institute of Technology, 2007. (in Chinese)
[17] HARPER B A, HOLLAND G J. An updated parametric model of the tropical cyclone [C]// Proceedings of the 23rd Conference on Hurricanes and Tropical Meteorology. Dallas: American Meteorological Society, 1999: 10 − 15.
[18] NOLAN D S, MCNOLDY B D, YUNGE J, et al. Evaluation of the surface wind field over land in WRF simulations of Hurricane Wilma (2005). Part II: Surface winds, inflow angles, and boundary layer profile [J]. Monthly Weather Review, 2021, 149(3): 697 − 713.
[19] PAN Y, CHEN Y P, LI J X, et al. Improvement of wind field hindcasts for tropical cyclones [J]. Water Science and Engineering, 2016, 9(1): 58 − 66. doi: 10.1016/j.wse.2016.02.002
[20] 郑笑, 沈晓鹏. 琼州海峡跨海铁路通道分期建设方案研究[J]. 铁道运输与经济, 2022, 44(10): 144 − 148. doi: 10.16668/j.cnki.issn.1003-1421.2022.10.21 ZHENG Xiao, SHEN Xiaopeng. Study on phased construction scheme of Qiongzhou strait railway [J]. Railway Transport and Economy, 2022, 44(10): 144 − 148. (in Chinese) doi: 10.16668/j.cnki.issn.1003-1421.2022.10.21
[21] 刘高, 张喜刚, 陈上有, 等. 特大型桥梁风-浪-流耦合作用[M]. 北京: 人民交通出版社股份有限公司, 2018: 6 − 8. LIU Gao, ZHANG Xigang, CHEN Shangyou, et al. Wind-wave-current coupling action of super-large bridge [M]. Beijing: People's Transportation Publishing House Co., Ltd., 2018: 6 − 8.
[22] YIN K, XU S D, HUANG W R. Estimating extreme sea levels in Yangtze Estuary by quadrature joint probability optimal sampling method [J]. Coastal Engineering, 2018, 140: 331 − 341. doi: 10.1016/j.coastaleng.2018.08.007
[23] SKLAR M. Fonctions de répartition à N dimensions et leurs marges [J]. Annales de l'ISUP, 1959, 8(3): 229 − 231.
[24] GENEST C, FAVRE A C. Everything you always wanted to know about copula modeling but were afraid to ask [J]. Journal of Hydrologic Engineering, 2007, 12(4): 347 − 368. doi: 10.1061/(ASCE)1084-0699(2007)12:4(347)
[25] 王涛, 尹宝树, 侯一筠, 等. 海浪等随机变量有界概率分布及工程应用[J]. 海洋工程, 2003, 21(3): 89 − 93. doi: 10.3969/j.issn.1005-9865.2003.03.015 WANG Tao, YIN Baoshu, HOU Yijun, et al. Bounded probability distribution and engineering applications of random variables such as waves [J]. The Ocean Engineering, 2003, 21(3): 89 − 93. (in Chinese) doi: 10.3969/j.issn.1005-9865.2003.03.015
[26] ZHANG J X, ZHANG M J, JIANG X L, et al. Pair-Copula-based trivariate joint probability model of wind speed, wind direction and angle of attack [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2022, 225: 105010. doi: 10.1016/j.jweia.2022.105010
[27] 邹志利. 水波理论及其应用[M]. 北京: 科学出版社, 2005: 468 − 469. ZOU Zhili. Water wave theories and their application [M]. Beijing: Science Press, 2005: 468 − 469.
计量
- 文章访问数: 62
- HTML全文浏览量: 33
- PDF下载量: 12
