A FULLY EDGE-BASED SMOOTHED FINITE ELEMENT METHOD FOR UPPER-BOUND LIMIT ANALYSIS OF AXISYMMETRIC STRUCTURES
-
摘要:
根据极限分析的机动定理，本文建立了轴对称结构极限上限分析的完全边光滑有限元法。为了避免复杂的坐标映射和雅可比矩阵的计算，对形函数的偏导项和非偏导项分别采用光滑应变技术与光滑积分伪弱形式进行处理，从而将所有的域积分都转化为更为简单的边界积分。考虑了材料的不可压缩条件，并采用罚函数法将其引入。为了克服目标函数非光滑导致的计算困难，采用了逐步识别刚性区和塑性区的方案，不断修正目标函数。数值算例结果表明，本文所提方法具有格式简单、计算效率高和收敛快等优点，并且对极度不规则单元同样可获得较高的计算精度。
Abstract:Based on the kinematic theorem of limit analysis, a fully smoothed edge-based finite element method is developed for upper bound limit analysis of axisymmetric structures. In order to completely avoid the complex coordinate mapping and calculation of Jacobian matrix, the partial derivative and non-partial derivative of shape functions are treated respectively by the smoothing strain technique and the quasi-weak form of smoothed integral. As a result, all the smoothed domain integrals can be converted into boundary integrals in the smoothing domains, which are relatively simpler. The plastic incompressibility can be introduced conveniently by the penalty function. By distinguishing the rigid zones from the plastic zones generally and by modifying the objective function accordingly at each iteration, the difficulties caused by a non-smoothness objective function can be easily overcome. Numerical examples show that the method proposed has some advantages such as simple formulation, high efficiency and fast convergence. In addition, high computational accuracy can also be obtained even though the extremely irregular elements are employed.
-
相对于传统的弹塑性增量法，极限分析不考虑加载路径，直接在比例加载条件下评估结构的极限载荷，具有更广泛的应用前景[1 − 3]。轴对称结构在工程中非常常见，其几何形状、约束条件和作用的载荷都对称于某一固定轴。对轴对称结构进行极限分析[4 − 6]并评估轴对称结构的极限载荷，可以充分发挥材料的承载性能，并产生明显的经济效益。
有限元法虽然已经成为解决工程问题的一个重要而且成熟的数值方法，但在处理网格畸变时往往表现无力[7]。为了克服网格畸变敏感性，研究者们提出了很多的高性能单元构造方法，如龙驭球和岑松等[8 − 9]提出的四边形面积坐标法、陈万吉等[10 − 11]提出的等参拟协调元法和精化不协调元法、陈娟和李崇君等[12 − 13]提出的四边形单元面积坐标插值新方法等。无网格法[14 − 15]对网格的依赖性弱，避免了有限元法中可能出现的网格畸变和扭曲，然而无网格法近似函数一般均很复杂，其计算量较大。光滑有限元法(S-FEM)[16 − 17]是一种将无网格法中光滑应变技术引入有限元框架体系的方法，具有对网格畸变不敏感和计算效率高等优点。目前已发展了多种光滑有限元法[18 − 22]，其中边光滑有限元法(ES-FEM)在计算平面问题时被证明具有最佳的稳定性和精度[23]。但光滑有限元只能处理轴对称结构中形函数的偏导项，对于非偏导项仍需采用等参单元进行计算。完全光滑技术[24 − 25]不仅采用光滑应变技术处理了形函数偏导项，还基于不定积分和高斯散度定理提出了一种光滑积分伪弱形式[26]对非偏导项进行处理，完全不需要复杂的坐标映射以及雅可比矩阵的计算。
鉴于完全光滑技术的优越性，本文建立了基于完全边光滑有限元法的轴对称结构极限上限分析的求解格式，并采用直接迭代算法[27]进行数值分析和研究。在三角形单元的基础上构造边界光滑域，对形函数的偏导项和非偏导项分别采用光滑应变技术和光滑积分伪弱形式进行处理，从而将所有的光滑域的域积分都转化为光滑域的边界积分。采用罚函数法引入材料的不可压缩条件，并通过将光滑域划分为刚性区和塑性区子集的方法克服了目标函数非光滑导致的困难。最后通过典型算例的计算和对比分析，验证了所提轴对称结构极限上限分析方法的有效性和合理性。
1 完全边光滑有限元法
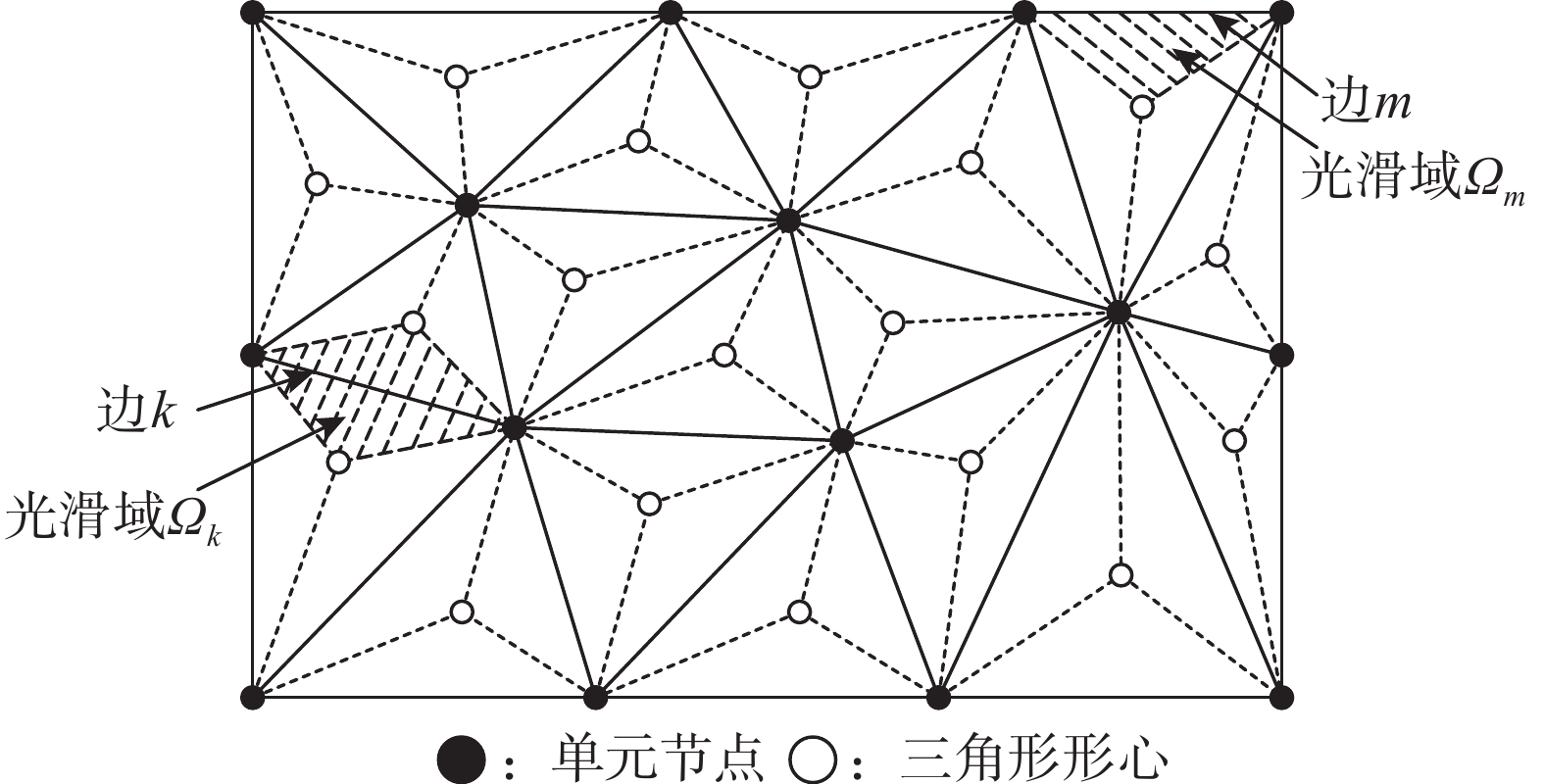
以轴对称面Ω内的三角形单元为背景单元，如图1所示，将每条单元边的端点与相邻三角形单元的形心按顺序连接，得到了与该边相关的光滑域，整个轴对称面Ω共有N个光滑域。
![]()
图 1 基于三角形单元的边光滑域Figure 1. The edge-based smoothing domains based on the triangular elements任意三角形单元内应变可表示为
\varepsilon (x) = {\{ {\varepsilon _r}{\text{ }}{\varepsilon _{\textit{z}}}{\text{ }}{\gamma _{r{\textit{z}}}}{\text{ }}{\varepsilon _\theta }\} ^{\rm{T}}} = \sum\limits_{i = 1}^3 {{{\boldsymbol{B}}_i}(x){{\boldsymbol{u}}_i}} (1) 式中： {{\boldsymbol{u}}_i} = {\left[ {{u_i},{v_i}} \right]^{\rm{T}}} 为节点位移；应变矩阵 {{\boldsymbol{B}}_i}(x) 的具体表达式为：
{{\boldsymbol{B}}_i}(x) = \left[ \begin{matrix} {\dfrac{{\partial {N_i}}}{{\partial r}}}&0 \\ 0&{\dfrac{{\partial {N_i}}}{{\partial {\textit{z}}}}} \\ {\dfrac{{\partial {N_i}}}{{\partial {\textit{z}}}}}&{\dfrac{{\partial {N_i}}}{{\partial r}}} \\ {\dfrac{{{N_i}}}{r}}&0 \end{matrix} \right] (2) 式中， {N_i} 为有限元形函数。
在光滑域{\varOmega _k}内对应变 \varepsilon (x) 进行光滑处理，我们有：
{\overline \varepsilon _k} = {\overline {\boldsymbol{B}}_k}{\boldsymbol{u}}_k^s = [\overline {\boldsymbol{B}}_k^1{\text{ }}\overline {\boldsymbol{B}}_k^2{\text{ }} \cdots {\text{ }}\overline {\boldsymbol{B}}_k^{{N_n}}]{\boldsymbol{u}}_k^s (3) 式中： {\boldsymbol{u}}_k^s 为光滑域{\varOmega _k}内节点位移向量； {N_n} 为支持节点总数，且：
\begin{split} \overline {\boldsymbol{B}}_k^i(x) = &\dfrac{{\text{1}}}{{{A_k}}}\int_{{\varOmega _k}} {{{\boldsymbol{B}}_i}} (x){\text{d}}\varOmega =\\& \dfrac{{\text{1}}}{{{A_k}}}\int_{{\varOmega _k}} {{{\left[ \begin{matrix} {\dfrac{{\partial {N_i}}}{{\partial r}}}&0&{\dfrac{{\partial {N_i}}}{{\partial {\textit{z}}}}}&{\dfrac{{{N_i}}}{r}} \\ 0&{\dfrac{{\partial {N_i}}}{{\partial {\textit{z}}}}}&{\dfrac{{\partial {N_i}}}{{\partial r}}}&0 \end{matrix} \right]}^{\text{T}}}} {\text{d}}\varOmega \end{split} (4) 式中， {A_k} 为光滑域{\varOmega _k}的面积。显然，光滑应变矩阵 \overline {\boldsymbol{B}}_k^i(x) 包含形函数的偏导项和非偏导项。采用散度定理可将与形函数偏导项相关的域积分直接转换为光滑域的边界积分，即：
\overline {\boldsymbol{B}}_k^i(x) = \left[ \begin{matrix} {\dfrac{{\text{1}}}{{{A_k}}}\displaystyle\int_{{\varGamma _k}} {{n_r}} {N_i}d\varGamma }&0 \\ 0&{\dfrac{{\text{1}}}{{{A_k}}}\displaystyle\int_{{\varGamma _k}} {{n_{\textit{z}}}} {N_i}d\varGamma } \\ {\dfrac{{\text{1}}}{{{A_k}}}\displaystyle\int_{{\varGamma _k}} {{n_{\textit{z}}}} {N_i}d\varGamma }&{\dfrac{{\text{1}}}{{{A_k}}}\displaystyle\int_{{\varGamma _k}} {{n_r}} {N_i}d\varGamma } \\ {\dfrac{{\text{1}}}{{{{\overline r}_k}{A_k}}}\displaystyle\int_{{\varOmega _k}} {{N_i}} d\varOmega }&0 \end{matrix} \right] = \left[ \begin{matrix} {\overline b_{ir}^k}&0 \\ 0&{\overline b_{i{\textit{z}}}^k} \\ {\overline b_{i{\textit{z}}}^k}&{\overline b_{ir}^k} \\ {\overline b_{ih}^k}&0 \end{matrix} \right] (5) 式中：{n_r}和{n_{\textit{z}}}分别为光滑域边界{\varGamma _k}的外法线与坐标轴r和z方向夹角的余弦值；{\overline r_k}为光滑域{\varOmega _k}中心点到对称轴的长度； \overline b_{ir}^k 和 \overline b_{i{\textit{z}}}^k 为沿光滑域边界的线积分，通过引入高斯积分， \overline b_{ir}^k 和 \overline b_{i{\textit{z}}}^k 可进一步写为：
\overline b_{ir}^k = \frac{{\text{1}}}{{{A_k}}}\sum\limits_{m = {\text{1}}}^{{N_s}} {\sum\limits_{n = {\text{1}}}^{{N_g}} {\frac{{\text{1}}}{{\text{2}}}} } {w_{m,n}}n_r^m{N_i}(x_{m,n}^g){l_m} (6) \overline b_{i{\textit{z}}}^k = \frac{{\text{1}}}{{{A_k}}}\sum\limits_{m = {\text{1}}}^{{N_s}} {\sum\limits_{n = {\text{1}}}^{{N_g}} {\frac{{\text{1}}}{{\text{2}}}} } {w_{m,n}}n_{\textit{z}}^m{N_i}(x_{m,n}^g){l_m} (7) 式中：x_{m,n}^g为光滑域边界{\varGamma _{k,m}}(m = 1,2, \cdots ,{N_s})上的高斯积分点；{w_{m,n}}为高斯积分点对应的权系数；{N_g}为各条光滑域边界上的高斯积分点数；{l_m}为光滑域边界的长度。
由于 \overline b_{ih}^k 中的积分项为形函数非偏导项，需要采用光滑积分伪弱形式[28, 29]进行降维积分，且 \overline b_{ih}^k 可重写为：
\begin{split} \overline b_{ih}^k = &\frac{1}{{{{\overline r}_k}{A_k}}}\int_{{\varGamma _k}} {{{\hat N}_i}(r,{\textit{z}})} {n_r}d\varGamma = \\& \frac{1}{{{{\overline r}_k}{A_k}}}\sum\limits_{m = 1}^{{N_s}} {\sum\limits_{n = 1}^{{N_g}} {\frac{1}{2}} } {w_{m,n}}n_r^m{{\hat N}_i}(x_{m,n}^g){l_m} \end{split} (8) 且：
{\hat N_i}(r,{\textit{z}}) = \int {{N_i}(r,{\textit{z}})dr} (9) 2 极限上限分析
考虑一个不计体力的理想刚塑性结构V，在边界{\varGamma _u}和边界{\varGamma _t}上分别作用有位移约束{u_i} = {\text{0}}和基准力系{p_i}，在体内满足不可压条件 {u_{i,i}} = 0 。结构在比例加载力系\eta {p_i}的作用下达到极限状态，\eta 为极限载荷乘子。当采用von-Mises屈服条件时，计算极限载荷乘子\eta 的数学规划格式可写为[30]：
\eta = \min:\sqrt {\frac{2}{3}} {\sigma _s}\int_V {\sqrt {{\varepsilon _{ij}}{\varepsilon _{ij}}} } {\mathrm{d}}V (10) {\mathrm{s.t.}} \;\;\;\int_{{\varGamma _t}} {{u_i}{p_i}} {\mathrm{d}}\varGamma = 1 \;\;\;{\mathrm{on}}\;\; {\varGamma _t} (11) {u_{i,i}} = 0\;\; {\mathrm{in}}\;\; V (12) {u_i} = {\text{0}} \;\;{\text{on }}\;\;{\varGamma _u} (13) 式中：{\sigma _s}为材料的屈服应力；{\varepsilon _{ij}}为机动允许的应变率； {u_i} 为机动允许的位移速度场。
将轴对称面\varOmega 离散成N个光滑域，则目标函数式(10)可写为：
\eta = \min :\sqrt {\frac{{\text{2}}}{{\text{3}}}} {\sigma _s}\sum\limits_{k = 1}^N {{A_k}\sqrt {{{({\boldsymbol{u}}_k^s)}^{\text{T}}}{{\overline {\boldsymbol{K}}}_k}{\boldsymbol{u}}_k^s} } {\text{2}}\pi {\overline r_k} (14) 式中， {\overline {\boldsymbol{K}}_k} 为光滑域{\varOmega _k}的刚度矩阵，且：
{\overline {\boldsymbol{K}}_k} = \overline {\boldsymbol{B}}_k^{\rm{T}}{\boldsymbol{D}}{\overline {\boldsymbol{B}}_k} (15) 式中：
{\boldsymbol{D}} = \left[ \begin{matrix} 1&0&0&0 \\ 0&1&0&0 \\ 0&0&{0.5}&0 \\ 0&0&0&1 \end{matrix} \right] (16) 约束条件式(11)经离散后可得
{{\boldsymbol{F}}^{\text{T}}}{\boldsymbol{U}} = {\text{1}} (17) 式中： {\boldsymbol{F}} 为等效载荷列向量；{\boldsymbol{U}}为总体的节点位移向量。在光滑域{\varOmega _k}内，塑性不可压条件式(12)可写为：
{{\boldsymbol{u}}_{i,i}} = {\overline \varepsilon _r} + {\overline \varepsilon _{\textit{z}}} + {\overline \varepsilon _\theta } = \overline {\boldsymbol{B}}_k^c{\boldsymbol{u}}_k^s = {\text{0}} (18) 式中：
\overline {\boldsymbol{B}}_k^c = [ {\overline {\boldsymbol{B}}_k^{c1}\;\;\overline {\boldsymbol{B}}_k^{c2}\;\; \cdots \;\;\overline {\boldsymbol{B}}_k^{c{N_n}}} ] (19) \overline {\boldsymbol{B}}_k^{ci} = [ {\overline b_{ir}^k + \overline b_{ih}^k}\;\;{\overline b_{i{\textit{z}}}^k} ] (20) 进一步，式(18)可写为：
{\left( {{{\overline \varepsilon }_r} + {{\overline \varepsilon }_{\textit{z}}} + {{\overline \varepsilon }_\theta }} \right)^2} = {({\boldsymbol{u}}_k^s)^{\rm{T}}}\overline {\boldsymbol{K}}_k^c{\boldsymbol{u}}_k^s = {\text{0}} (21) 式中：
\overline {\boldsymbol{K}}_k^c = {(\overline {\boldsymbol{B}}_k^c)^{\rm{T}}}\overline {\boldsymbol{B}}_k^c (22) 根据上述推导过程，由光滑域节点位移向量 {\boldsymbol{u}}_k^s 组成总体节点位移向量{\boldsymbol{U}}，并将 {\overline {\boldsymbol{K}}_k} 和 \overline {\boldsymbol{K}}_k^c 扩展为与{\boldsymbol{U}}同阶，则轴对称结构极限上限分析离散化的数学规划格式可写为：
\eta = \min :\sum\limits_{k \in I} {{\rho _k}\sqrt {{{\boldsymbol{U}}^{\text{T}}}{{\overline {\boldsymbol{K}}}_k}{\boldsymbol{U}}} } (23) {\mathrm{s.t.}}\;\;{{\boldsymbol{F}}^{\text{T}}}{\boldsymbol{U}} = {\text{1}} (24) {{\boldsymbol{U}}^{\text{T}}}\overline {\boldsymbol{K}}_k^c{\boldsymbol{U}} = {\text{0 (}}k \in I) (25) 式中，I为全部光滑域的集合，且：
{\rho _k} = 2\pi \sqrt {\frac{2}{3}} {\sigma _s}{A_k}{\overline r_k} (26) 采用拉格朗日乘子q将约束条件式(24)引入目标函数中，则式(23)~式(25)所示的数学规划问题可表示为：
L(U,q) = \min :\sum\limits_{k \in I} {{\rho _k}\sqrt {{{\boldsymbol{U}}^{\text{T}}}{{\overline {\boldsymbol{K}}}_k}{\boldsymbol{U}}} } - q({{\boldsymbol{F}}^{\rm{T}}}{\boldsymbol{U}} - {\text{1}}) (27) {\text{s}}{\text{.t}}{\text{. }}{{\boldsymbol{U}}^{\rm{T}}}\overline {\boldsymbol{K}}_k^c{\boldsymbol{U}} = {\text{0 (}}k \in I) (28) 若设想任意光滑域内应变均不为零，即：
{{\boldsymbol{U}}^{\text{T}}}{\overline {\boldsymbol{K}}_k}{\boldsymbol{U}} \ne {\text{0 (}}k \in I) (29) 则目标函数式(27)~式(28)的极小化条件可写为：
\sum\limits_{k \in I} {{\rho _k}\frac{{{{\overline {\boldsymbol{K}}}_k}{\boldsymbol{U}}}}{{\sqrt {{{\boldsymbol{U}}^{\text{T}}}{{\overline {\boldsymbol{K}}}_k}{\boldsymbol{U}}} }}} = q{\boldsymbol{F}} (30) {{\boldsymbol{F}}^{\rm{T}}}{\boldsymbol{U}} = {\text{1}} (31) {{\boldsymbol{U}}^{\text{T}}}\overline {\boldsymbol{K}}_k^c{\boldsymbol{U}} = {\text{0 (}}k \in I) (32) 为便于式(30)~式(32)所示非线性方程组的求解，我们构造新的迭代格式如下：
\sum\limits_{k \in I} {{\rho _k}\frac{{{{\overline {\boldsymbol{K}}}_k}{{\boldsymbol{U}}_ i}}}{{\sqrt {{{\boldsymbol{U}}_ {i - {\text{1}}}}^{\text{T}}{{\overline {\boldsymbol{K}}}_k}{{\boldsymbol{U}}_ {i - {\text{1}}}}} }}} = {q_i}{\boldsymbol{F}} (33) {{\boldsymbol{F}}^{\rm{T}}}{{\boldsymbol{U}}_ i} = {\text{1}} (34) {\boldsymbol{U}}_ i^{\text{T}}\overline {\boldsymbol{K}}_k^c{{\boldsymbol{U}}_ i} = {\text{0 (}}k \in I) (35) 式中：{{\boldsymbol{U}}_ {i - 1}}和{{\boldsymbol{U}}_ i}分别为第i - 1迭代步和第i迭代步的节点位移向量；{q_i}为第i迭代步的拉格朗日乘子。在进行第i步迭代前，需将全部光滑域的集合I划分为刚性区子集{R_i}和塑性区子集{P_i}：
I = {P_i} \cup {R_i} (36) {P_i} = \{ k \in I,{\boldsymbol{U}}_ {i - 1}^{\rm{T}}{\overline {\boldsymbol{K}}_k}{{\boldsymbol{U}}_ {i - 1}} \ne {\text{0}}\} {\text{ }} (37) {R_i} = \{ k \in I,{\boldsymbol{U}}_ {i - 1}^{\text{T}}{\overline {\boldsymbol{K}}_k}{{\boldsymbol{U}}_ {i - 1}} = {\text{0}}\} {\text{ }} (38) 综上所述，轴对称结构极限上限分析的离散数学规划格式可表达为：
\eta = \min :\sum\limits_{k \in {P_i}} {{\rho _k}\frac{{{\boldsymbol{U}}_ i^{\rm{T}}{{\overline {\boldsymbol{K}}}_k}{{\boldsymbol{U}}_ i}}}{{\sqrt {{{\boldsymbol{U}}_ {i - {\text{1}}}}^{\text{T}}{{\overline {\boldsymbol{K}}}_k}{{\boldsymbol{U}}_ {i - {\text{1}}}}} }}} (39) {\text{s}}{\text{.t}}{\text{. }}{{\boldsymbol{F}}^{\text{T}}}{{\boldsymbol{U}}_ i} = {\text{1}} (40) {\boldsymbol{U}}_ i^{\rm{T}}{\overline {\boldsymbol{K}}_k}{{\boldsymbol{U}}_ i} = 0 \;\;\;(k \in {R_i}) (41) {\boldsymbol{U}}_ i^{\rm{T}}\overline {\boldsymbol{K}}_k^c{{\boldsymbol{U}}_ i} = 0 \;\;\;(k \in {P_i}) (42) 采用拉格朗日乘子法消除约束条件式(40)，使用罚函数法对约束条件式(41)和式(42)进行处理，则求解的极小化问题可写为：
\begin{split} {L_i} = &\sum\limits_{k \in {P_i}} {{\rho _k}\frac{{{\boldsymbol{U}}_ i^{\rm{T}}{{\overline {\boldsymbol{K}}}_k}{{\boldsymbol{U}}_ i}}}{{\sqrt {{{\boldsymbol{U}}_ {i - {\text{1}}}}^{\text{T}}{{\overline {\boldsymbol{K}}}_k}{{\boldsymbol{U}}_ {i - {\text{1}}}}} }}} + \alpha \sum\limits_{k \in {P_i}} {{\rho _k}{\boldsymbol{U}}_i^{\rm{T}}\overline {\boldsymbol{K}}_k^c{{\boldsymbol{U}}_ i}} + \\& \beta \sum\limits_{k \in {R_i}} {{\rho _k}{\boldsymbol{U}}_i^{\rm{T}}{{\overline {\boldsymbol{K}}}_k}{{\boldsymbol{U}}_ i}} - 2{q_i}({{\boldsymbol{F}}^{\rm{T}}}{{\boldsymbol{U}}_ i} - {\text{1}}) \end{split} (43) 式中，\alpha 和\beta 为罚因子。
根据上述构想，基于完全边光滑有限元法的轴对称结构极限上限分析步骤可归纳为：
1) 假设初始状态下整个轴对称结构处于完全塑性状态，求解极小化问题：
\eta = \min :\sum\limits_{k \in I} {{\rho _k}{\boldsymbol{U}}_{\text{0}}^{\rm{T}}{{\overline {\boldsymbol{K}}}_k}{{\boldsymbol{U}}_ {\text{0}}}} (44) {\text{s}}{\text{.t}}{\text{. }}{{\boldsymbol{F}}^{\rm{T}}}{{\boldsymbol{U}}_ {\text{0}}} = {\text{1}} (45) {\boldsymbol{U}}_ {\text{0}}^{\text{T}}\overline {\boldsymbol{K}}_k^c{{\boldsymbol{U}}_ {\text{0}}} = {\text{0 (}}k \in I) (46) 通过求解以上的极小化问题，可得初始的极限载荷乘子为：
{\eta _{\text{0}}} = \sum\limits_{k \in I} {{\rho _k}\sqrt {{{\boldsymbol{U}}_ {\text{0}}}^{\text{T}}{{\overline {\boldsymbol{K}}}_k}{{\boldsymbol{U}}_ {\text{0}}}} } (47) 2) 根据位移向量{{\boldsymbol{U}}_ {i - 1}}将全部的光滑域划分刚性区子集{R_i}和塑性区子集{P_i}，并求解如下极小化问题：
\eta = \min :\sum\limits_{k \in {P_i}} {{\rho _k}\frac{{{\boldsymbol{U}}_ i^{\rm{T}}{{\overline {\boldsymbol{K}}}_k}{{\boldsymbol{U}}_ i}}}{{\sqrt {{{\boldsymbol{U}}_ {i - {\text{1}}}}^{\text{T}}{{\overline {\boldsymbol{K}}}_k}{{\boldsymbol{U}}_ {i - {\text{1}}}}} }}} (48) {\text{s}}{\text{.t}}{\text{. }}{{\boldsymbol{F}}^{\text{T}}}{{\boldsymbol{U}}_ i} = {\text{1}} (49) {\boldsymbol{U}}_ i^{\rm{T}}{\overline {\boldsymbol{K}}_k}{{\boldsymbol{U}}_ i} = 0 \;\;\;(k \in {R_i}) (50) {\boldsymbol{U}}_ i^{\rm{T}}\overline {\boldsymbol{K}}_k^c{{\boldsymbol{U}}_ i} = 0 \;\;\;(k \in {P_i}) (51) 通过求解以上的极小化问题，可得第i步的极限载荷乘子为：
{\eta _i} = \sum\limits_{k \in {P_i}} {{\rho _k}\sqrt {{\boldsymbol{U}}_ i^{\rm{T}}{{\overline {\boldsymbol{K}}}_k}{{\boldsymbol{U}}_ i}} } (52) 当上述迭代过程满足以下收敛条件时，迭代终止：
|{\eta _i} - {\eta _{i - {\text{1}}}}|/{\eta _i} {\leqslant} \varepsilon (53) 式中，\varepsilon 为根据计算所需精度确定的误差容限，且本文取\varepsilon = {\text{2}}{\text{.0}} \times {\text{1}}{{\text{0}}^{ - 4}}。
3 计算实例
3.1 厚壁圆筒
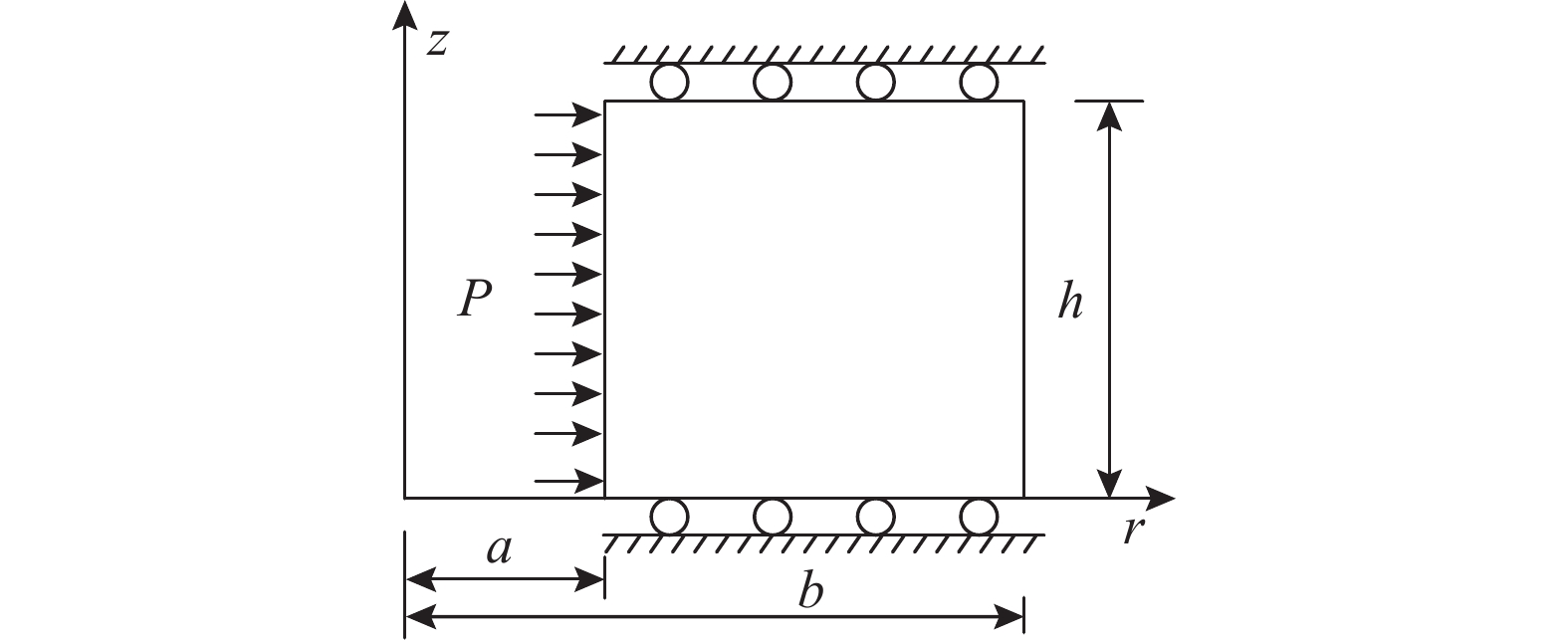
如图2所示，内半径为a，外半径为b的厚壁圆筒，在内表面处作用有均匀压力P。如果采用von Mises屈服准则，厚壁圆筒的极限载荷解析解可写为[1]：
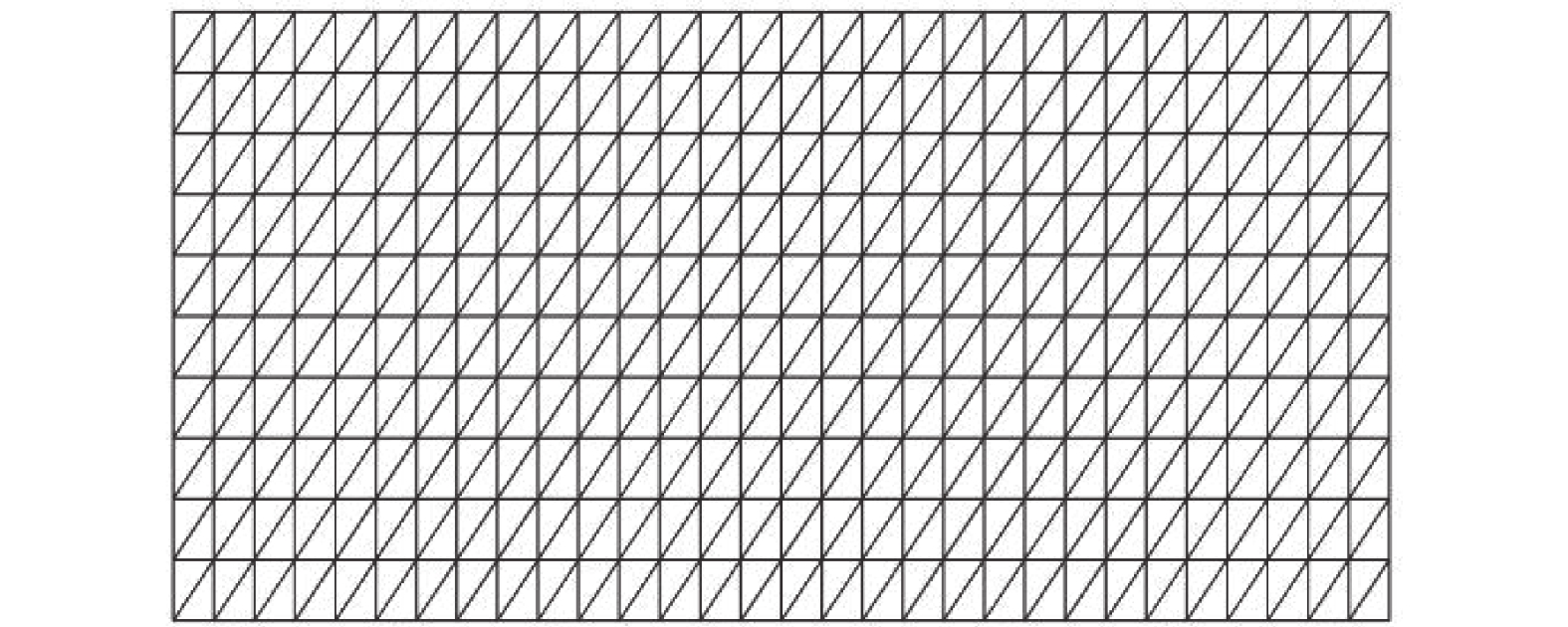
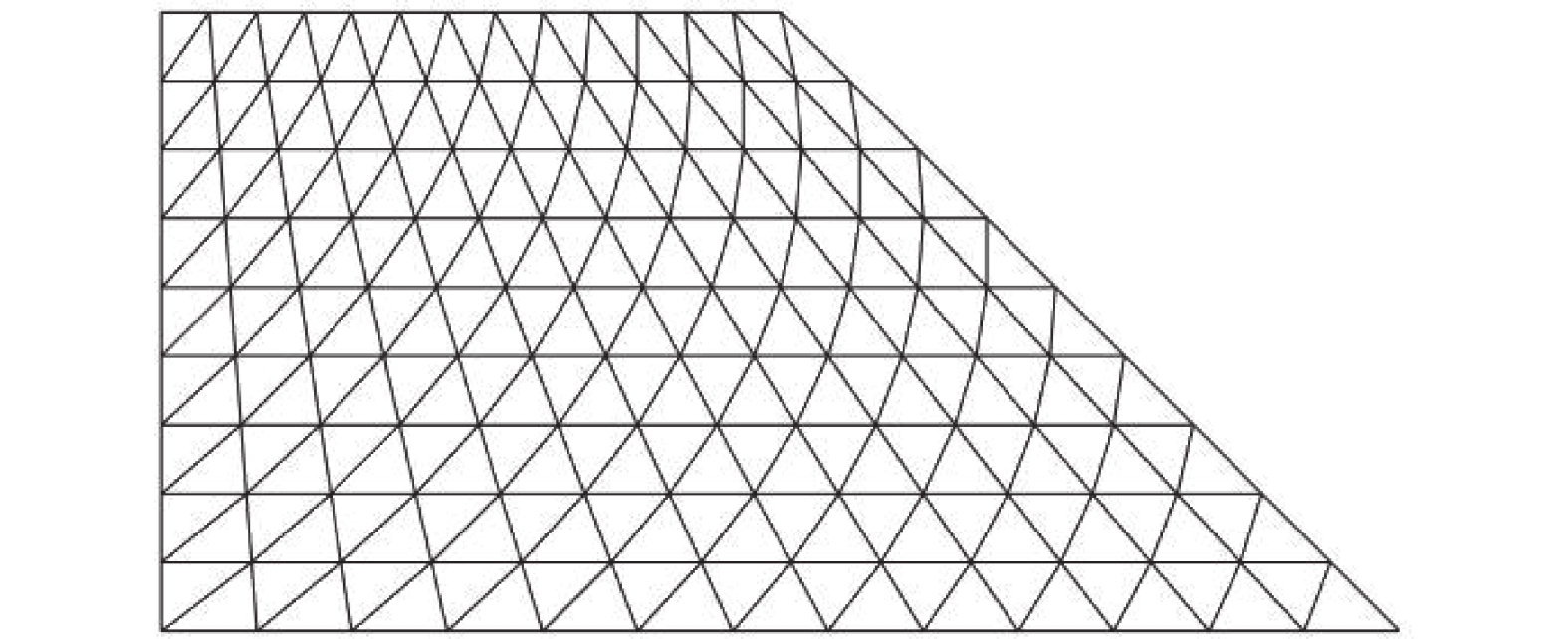
P = \frac{{{\text{2}}{\sigma _s}}}{{\sqrt {\text{3}} }}\ln \frac{b}{a} (54) 截取长h = a的一段进行计算，并且对于不同的外内径比b/a采用不同的单元划分方案。图3给出了b/a = {\text{3}}时单元划分情况。
![]()
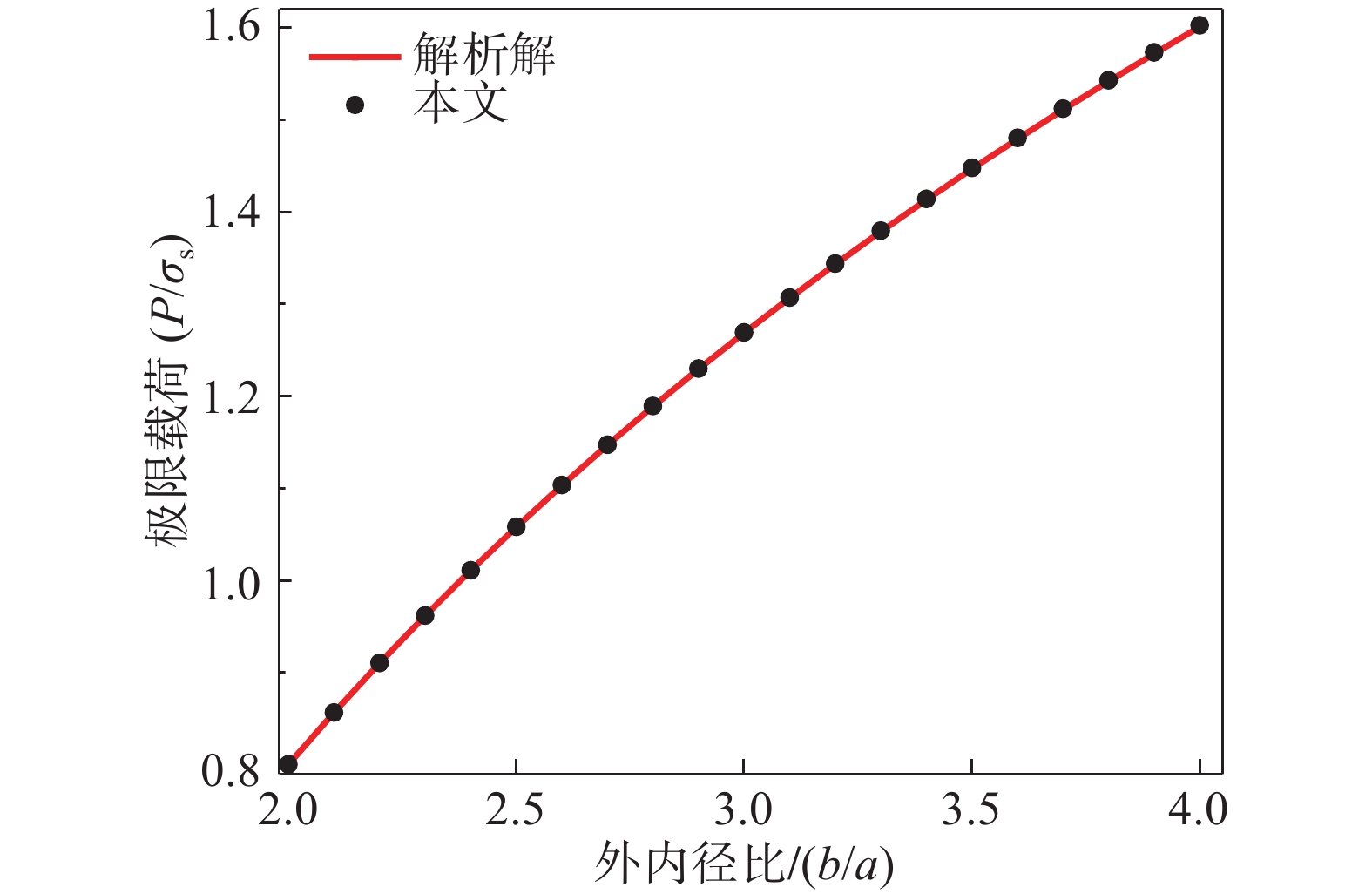
图 3 b/a = {\text{3}}时厚壁圆筒规则单元划分Figure 3. Regular elements for the thick-walled cylinder when b/a = {\text{3}}在图4中给本文的计算结果与相应的解析解进行了比较。可以发现，采用完全边光滑有限元法计算厚壁圆筒的极限载荷能取得较高的精度。
![]()
图 4 厚壁圆筒极限载荷数值解与解析解对比Figure 4. Numerical limit loads compared with analytical solutions for the thick-walled cylinder为了研究不规则单元对计算精度的影响，通过以下方法构建不规则单元：
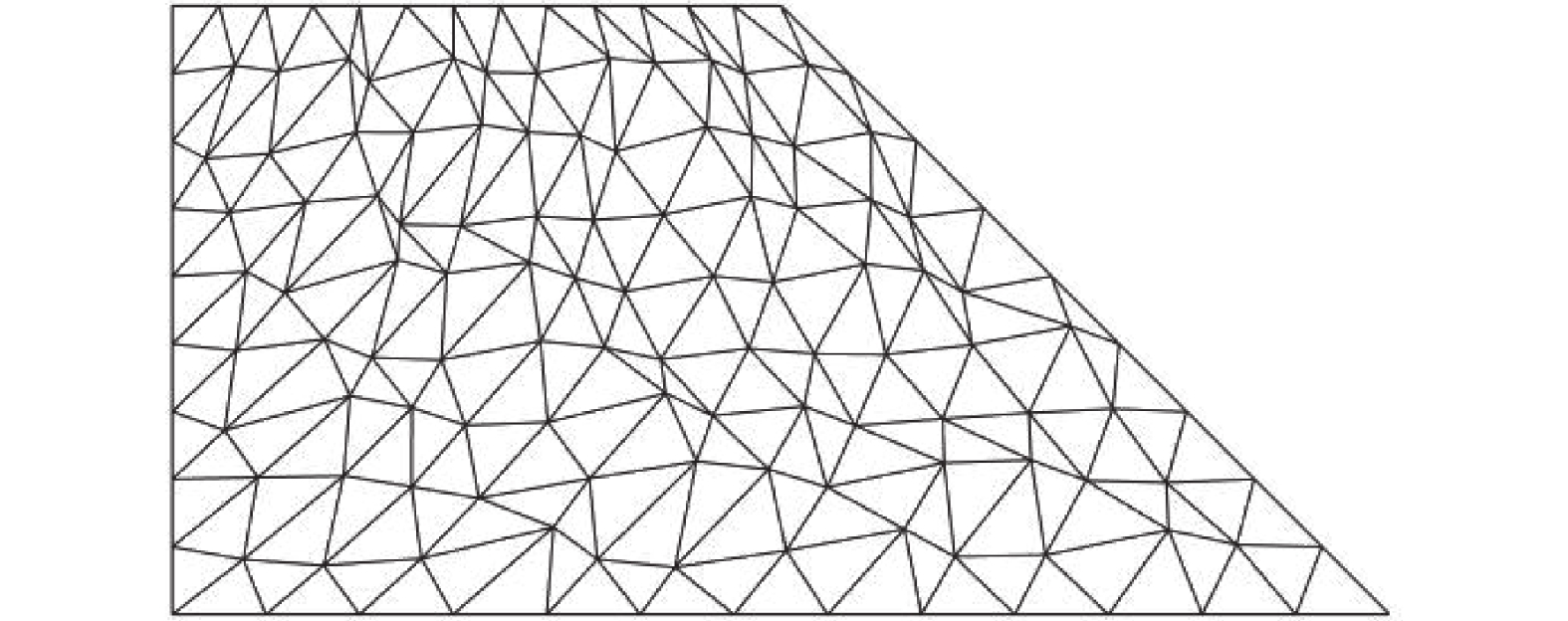
\begin{split} & {x_0} =x + \alpha \cdot r\Delta x \\& {y_0} = y + \alpha \cdot r\Delta y \end{split} (55) 式中：x和y为单元节点初始坐标；{x_0}和{y_0}为畸变后单元节点坐标；r为 - 1~1之间的随机数；\alpha 为单元不规则变形的畸变系数；\Delta x和\Delta y为初始单元长度。图5给出了畸变系数\alpha = {\text{0}}{\text{.5}}时厚壁圆筒的不规则单元划分情况。表1给出了不同畸变系数下b/a = {\text{3}}时厚壁圆筒的极限载荷，可以看出，即使采用极度不规则单元，本文计算结果与解析解的误差仍能保持在0.1%以下，进而说明本文方法具有很好的抗网格畸变能力。
![]()
图 5 \alpha = {\text{0}}{\text{.5}}时厚壁圆筒不规则单元划分Figure 5. Irregular elements for the thick-walled cylinder when \alpha = {\text{0}}{\text{.5}}表 1 不同畸变系数下b/a = {\text{3}}时厚壁圆筒的极限载荷Table 1. Limit loads of thick-walled cylinder with different irregularity factors when b/a = {\text{3}}畸变系数 解析解 本文 误差/(%) \alpha = 0.1 1.2686 1.2687 0.0079 \alpha = 0.2 1.2687 0.0079 \alpha = 0.3 1.2688 0.0158 \alpha = 0.4 1.2689 0.0236 \alpha = 0.5 1.2693 0.0552 3.2 厚壁球壳
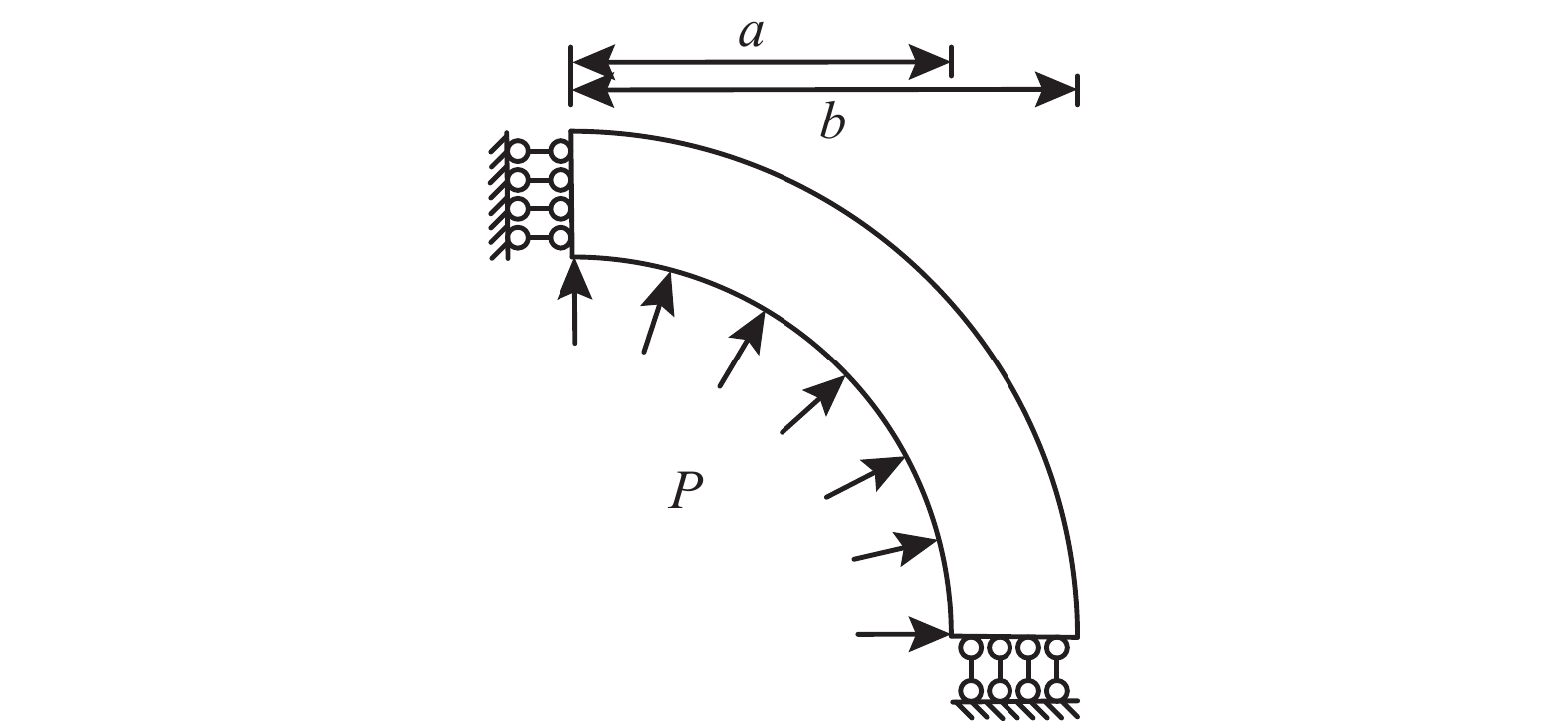
为了进一步验证本文方法的有效性，本文对图6所示厚壁球壳的极限内压P进行了计算。设球壳的内半径为a，外半径为b，则厚壁球壳的极限载荷解析解可表达为[1]：
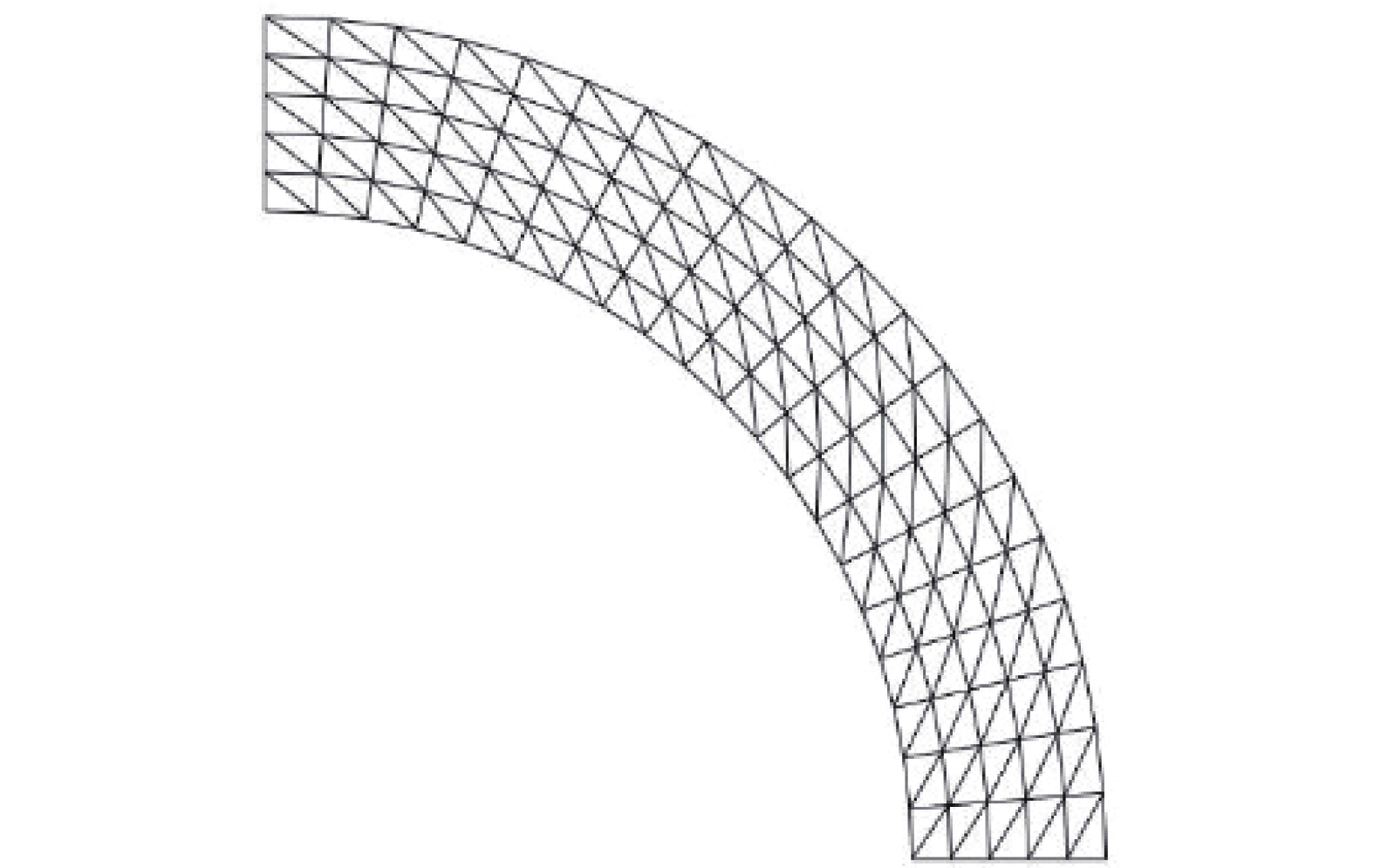
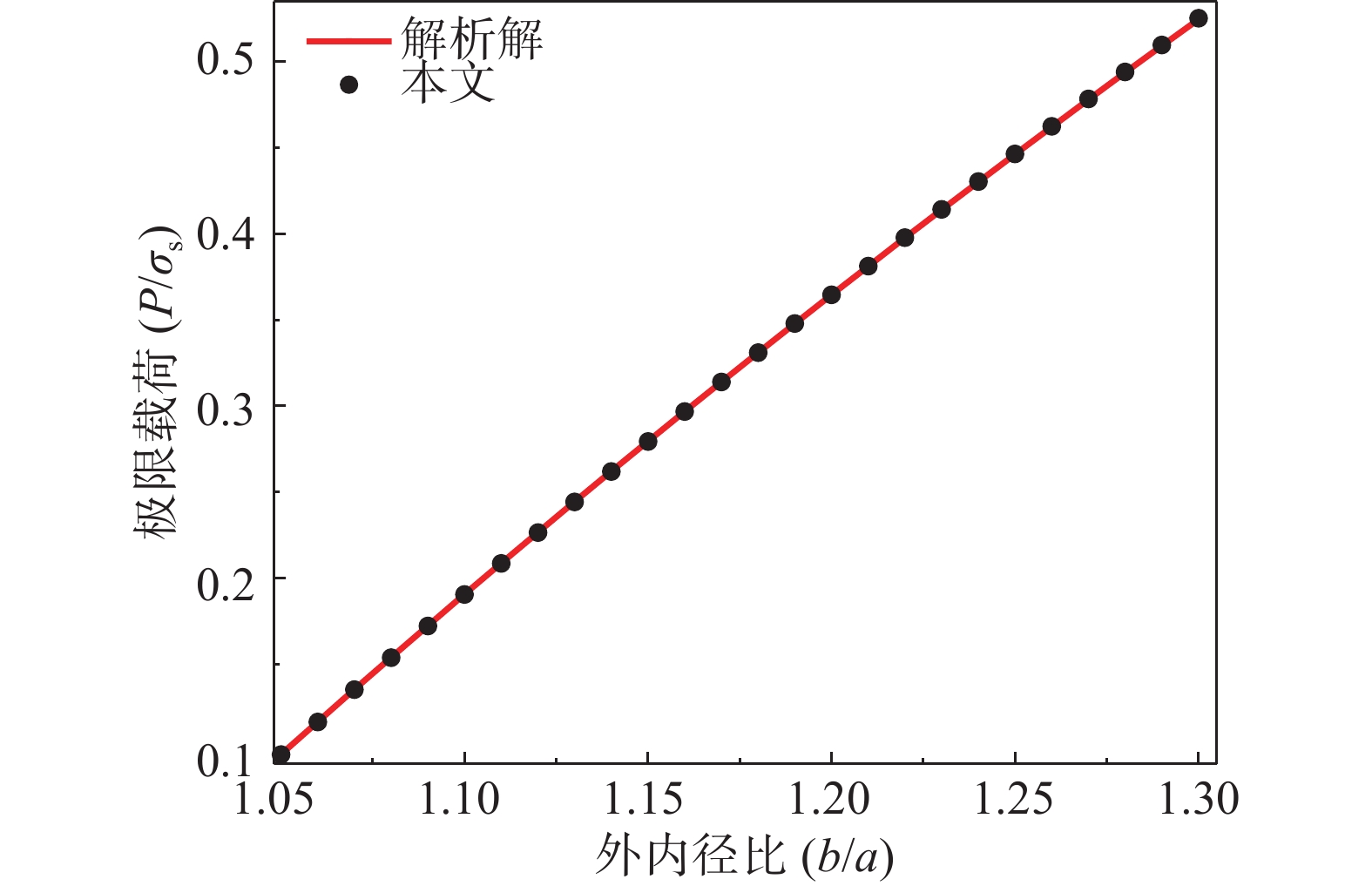
P = {\text{2}}{\sigma _s}\ln \frac{b}{a} (56) 对于不同的b/a，采用不同的单元划分方案，且图7给出了b/a = {\text{1}}{\text{.3}}时的单元划分情况。图8给出了 b/a = 1.05\sim 1.3 时本文计算的厚壁球壳极限载荷数值解与解析解的比较结果，可以看出结果吻合很好，进一步验证了本文方法的有效性。
![]()
图 7 b/a = {\text{1}}{\text{.3}}时厚壁球壳规则单元划分Figure 7. Regular elements for the thick-walled spherical shell when b/a = {\text{1}}{\text{.3}}![]()
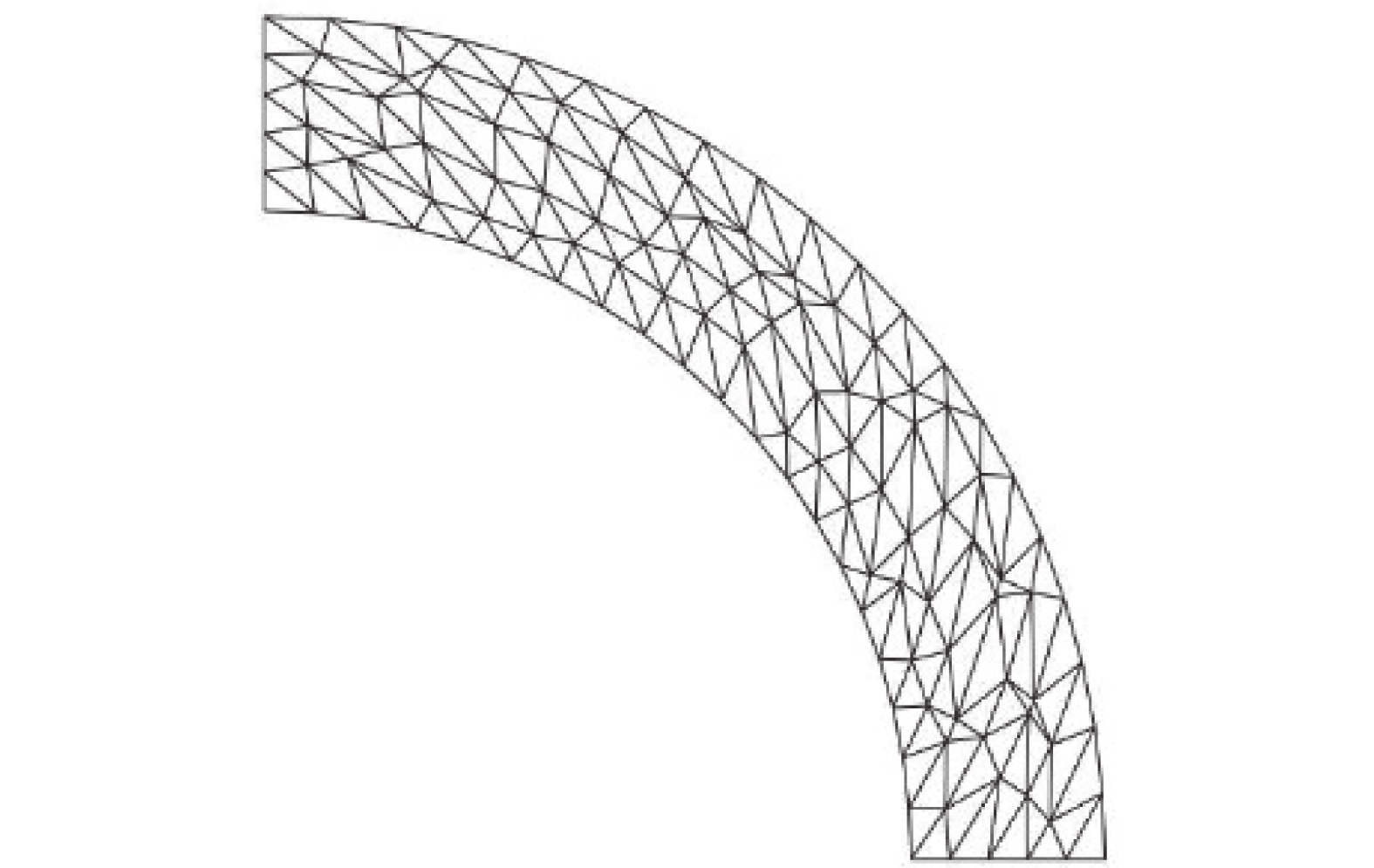
图 8 厚壁球壳极限载荷数值解与解析解对比Figure 8. Numerical limit loads compared with analytical solutions for the thick-walled spherical shell图9为畸变系数\alpha = {\text{0}}{\text{.5}}时b/a = 1.{\text{3}}的厚壁球壳不规则单元划分情况，且表2给出了不同畸变系数下b/a = 1.{\text{3}}时厚壁球壳的极限载荷数值解与解析解的对比。显然，不规则单元计算结果与解析解误差均保持在1%以下，可以验证本文方法对离散单元的质量要求较低。
![]()
图 9 \alpha = {\text{0}}{\text{.5}}时厚壁球壳不规则单元划分Figure 9. Irregular elements for the thick-walled spherical shell when \alpha = {\text{0}}{\text{.5}}表 2 不同畸变系数下b/a = 1.{\text{3}}时厚壁球壳的极限载荷Table 2. Limit loads of thick-walled spherical shell with different irregularity factors when b/a = 1.3畸变系数 解析解 本文 误差/(%) \alpha = 0.1 0.5247 0.5268 0.4002 \alpha = 0.2 0.5278 0.5908 \alpha = 0.3 0.5283 0.6861 \alpha = 0.4 0.5289 0.8005 \alpha = 0.5 0.5290 0.8195 3.3 厚壁圆台
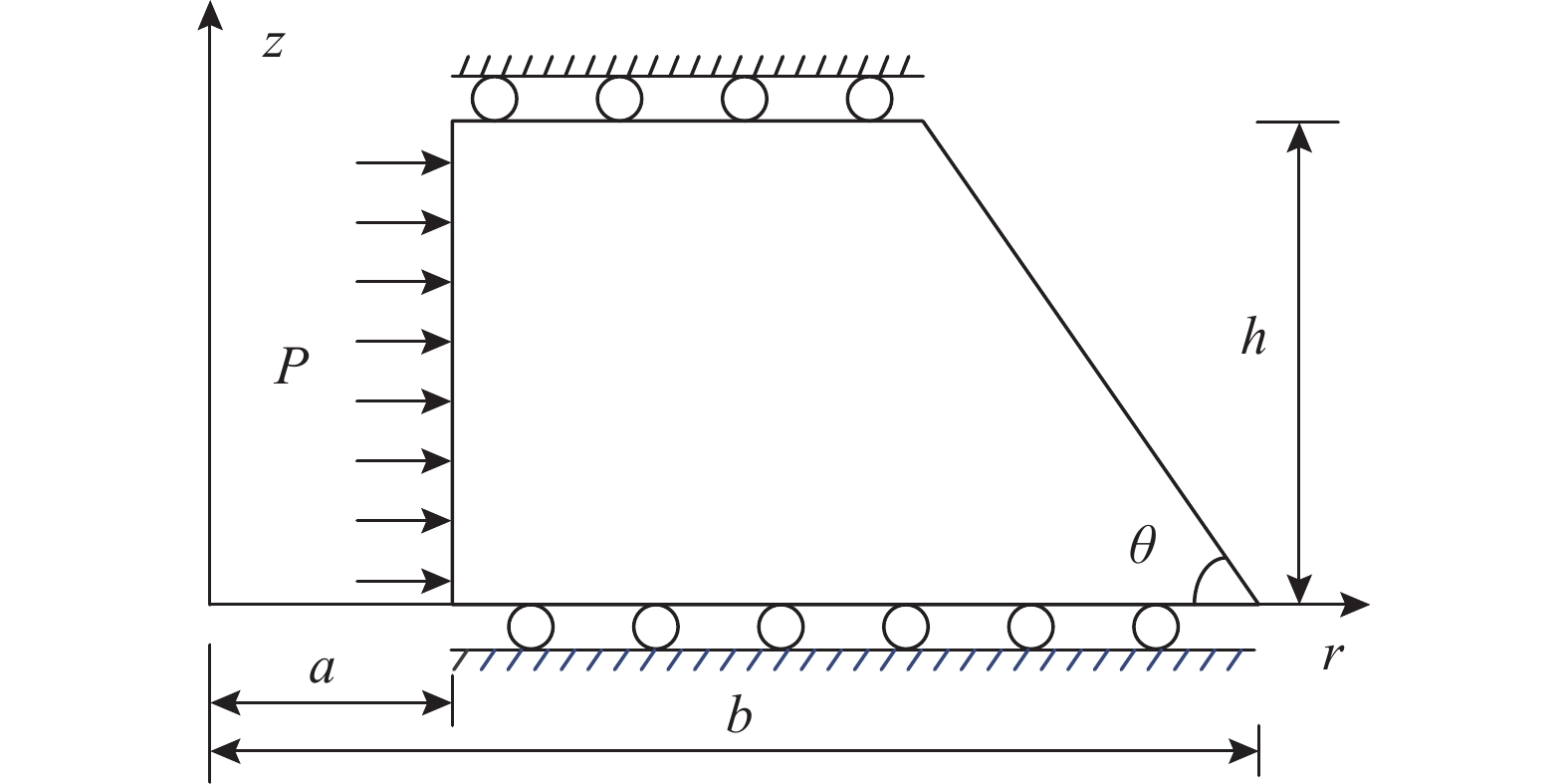
图10所示的厚壁圆台，底角为\theta ，底部内半径为a，外半径为b，且外半径与内半径之比b/a为2.0，圆台高度为h = 1.0，在内表面处作用的均布压力为P。
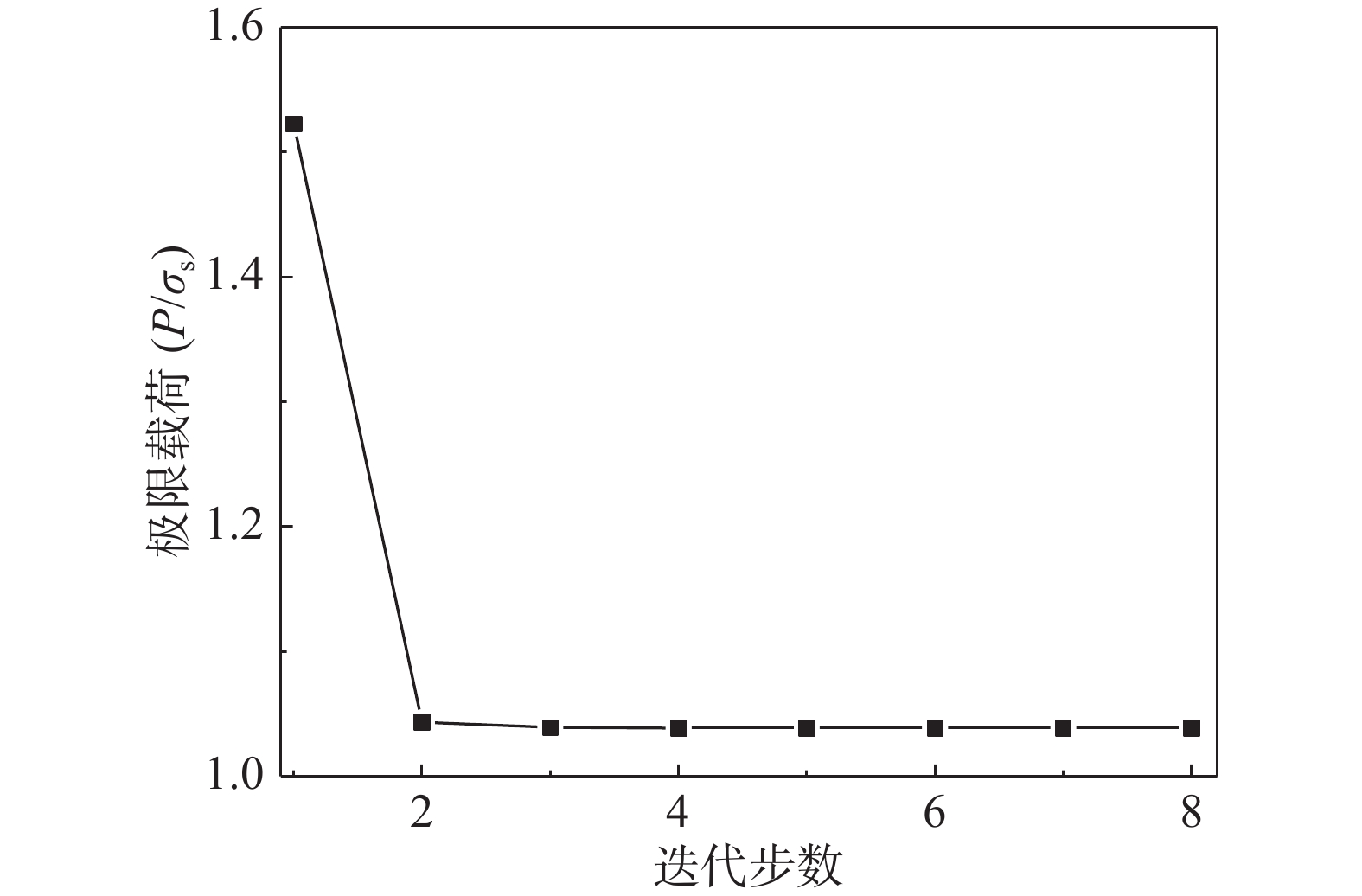
图11和图12分别给出了底角45^\circ 时厚壁圆台的规则单元和不规则单元(\alpha = 0.5)划分方案。本文分别对厚壁圆台底角\theta 取30^\circ 、45^\circ 、60^\circ 和75^\circ 时的极限载荷进行计算。图13给出了厚壁圆台在底角为45^\circ 时极限上限分析的迭代收敛示意图，可以看出，本文方法具有较好的收敛性。表3给出了不同底角厚壁圆台在不同畸变系数时极限载荷的计算结果，可以发现本文方法对网格畸变十分不敏感。
![]()
图 11 \theta = 45^\circ 时厚壁圆台规则单元划分Figure 11. Regular elements for the thick-walled round platform when \theta = 45^\circ![]()
图 12 \alpha = {\text{0}}{\text{.5}}时厚壁圆台不规则单元划分Figure 12. Irregular elements for the thick-walled round platform when \alpha = {\text{0}}{\text{.5}}![]()
图 13 \theta = 45^\circ 时厚壁圆台的极限上限分析迭代过程Figure 13. The iterative process for the upper bound limit analysis of the thick-walled round platform when \theta = 45^\circ表 3 厚壁圆台在不同底角时的极限载荷 (P/{\sigma _s})Table 3. Limit loads of the thick-walled round platform with different bottom angles (P/{\sigma _s})\theta /(°) \alpha = {\text{0}}{\text{.0}} \alpha = {\text{0}}{\text{.3}} \alpha = {\text{0}}{\text{.5}} {\text{30}} 1.176 1.176 1.178 {\text{45}} 1.038 1.038 1.041 {\text{60}} 0.950 0.950 0.953 {\text{75}} 0.879 0.879 0.882 4 结论
本文首次采用完全边光滑有限元法，建立了轴对称结构极限上限分析的求解算法。采用完全光滑技术完全避免了复杂的坐标映射和雅可比矩阵的计算，并采用直接迭代算法有效克服了目标函数非光滑导致的计算困难。由本文分析和计算结果可以看出：
(1) 完全边光滑有限元法可作为一种有效的数值方法用于轴对称结构极限上限分析。完全边光滑有限元法在光滑应变技术的基础上，运用光滑积分伪弱形式处理了形函数偏导项，将所有的光滑域的域积分都转化为光滑域的边界积分。计算结果表明该方法具有较高的计算效率和精度，且对极度不规则单元同样可获得较好的精度。
(2) 本文所采用的直接迭代算法具有较快的收敛速度，只需数次迭代就能获得指定误差容限内的极限载荷乘子，具有适用范围广、计算效率高、稳定性好等优点。
(3) 本文所提出的极限上限分析求解算法具有格式简单和易于程序实现的优点，可推广应用于求解复杂结构的极限与安定分析问题。
-
![]()
图 1 基于三角形单元的边光滑域
Figure 1. The edge-based smoothing domains based on the triangular elements
![]()
图 3 b/a = {\text{3}}时厚壁圆筒规则单元划分
Figure 3. Regular elements for the thick-walled cylinder when b/a = {\text{3}}
![]()
图 4 厚壁圆筒极限载荷数值解与解析解对比
Figure 4. Numerical limit loads compared with analytical solutions for the thick-walled cylinder
![]()
图 5 \alpha = {\text{0}}{\text{.5}}时厚壁圆筒不规则单元划分
Figure 5. Irregular elements for the thick-walled cylinder when \alpha = {\text{0}}{\text{.5}}
![]()
图 7 b/a = {\text{1}}{\text{.3}}时厚壁球壳规则单元划分
Figure 7. Regular elements for the thick-walled spherical shell when b/a = {\text{1}}{\text{.3}}
![]()
图 8 厚壁球壳极限载荷数值解与解析解对比
Figure 8. Numerical limit loads compared with analytical solutions for the thick-walled spherical shell
![]()
图 9 \alpha = {\text{0}}{\text{.5}}时厚壁球壳不规则单元划分
Figure 9. Irregular elements for the thick-walled spherical shell when \alpha = {\text{0}}{\text{.5}}
![]()
图 11 \theta = 45^\circ 时厚壁圆台规则单元划分
Figure 11. Regular elements for the thick-walled round platform when \theta = 45^\circ
![]()
图 12 \alpha = {\text{0}}{\text{.5}}时厚壁圆台不规则单元划分
Figure 12. Irregular elements for the thick-walled round platform when \alpha = {\text{0}}{\text{.5}}
![]()
图 13 \theta = 45^\circ 时厚壁圆台的极限上限分析迭代过程
Figure 13. The iterative process for the upper bound limit analysis of the thick-walled round platform when \theta = 45^\circ
表 1 不同畸变系数下b/a = {\text{3}}时厚壁圆筒的极限载荷
Table 1 Limit loads of thick-walled cylinder with different irregularity factors when b/a = {\text{3}}
畸变系数 解析解 本文 误差/(%) \alpha = 0.1 1.2686 1.2687 0.0079 \alpha = 0.2 1.2687 0.0079 \alpha = 0.3 1.2688 0.0158 \alpha = 0.4 1.2689 0.0236 \alpha = 0.5 1.2693 0.0552 
下载: 导出CSV
表 2 不同畸变系数下b/a = 1.{\text{3}}时厚壁球壳的极限载荷
Table 2 Limit loads of thick-walled spherical shell with different irregularity factors when b/a = 1.3
畸变系数 解析解 本文 误差/(%) \alpha = 0.1 0.5247 0.5268 0.4002 \alpha = 0.2 0.5278 0.5908 \alpha = 0.3 0.5283 0.6861 \alpha = 0.4 0.5289 0.8005 \alpha = 0.5 0.5290 0.8195
下载: 导出CSV
表 3 厚壁圆台在不同底角时的极限载荷 (P/{\sigma _s})
Table 3 Limit loads of the thick-walled round platform with different bottom angles (P/{\sigma _s})
\theta /(°) \alpha = {\text{0}}{\text{.0}} \alpha = {\text{0}}{\text{.3}} \alpha = {\text{0}}{\text{.5}} {\text{30}} 1.176 1.176 1.178 {\text{45}} 1.038 1.038 1.041 {\text{60}} 0.950 0.950 0.953 {\text{75}} 0.879 0.879 0.882
下载: 导出CSV
-
[1] 宋卫东. 塑性力学[M]. 北京: 科学出版社, 2017. (查阅网上资料, 未找到对应的页码信息, 请确认) . SONG Weidong. Plastic mechanics [M]. Beijing: Science Press, 2017. (in Chinese) (查阅网上资料, 未找到对应的英文翻译, 请确认) .
[2] 蒋宇洪, 杨娜. 基于极限分析的三叶墙抗压强度预测模型研究[J]. 工程力学, 2022, 39(2): 168 − 177, 188. doi: 10.6052/j.issn.1000-4750.2020.12.0941 JIANG Yuhong, YANG Na. A prediction model of the compressive strength of three-leaf walls based on limit analysis [J]. Engineering Mechanics, 2022, 39(2): 168 − 177, 188. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.12.0941
[3] CHEN S S, XU M Y, ZHU X Y. A cell-based smoothed radial point interpolation method applied to kinematic limit analysis of thin plates [J]. Engineering Analysis with Boundary Elements, 2022, 143: 710 − 718. doi: 10.1016/j.enganabound.2022.07.021
[4] 陈莘莘, 王崴. 基于自然单元法的轴对称结构极限上限分析[J]. 计算力学学报, 2020, 37(2): 159 − 164. doi: 10.7511/jslx20190121003 CHEN Shenshen, WANG Wei. Upper bound limit analysis of axisymmetric structures based on natural element method [J]. Chinese Journal of Computational Mechanics, 2020, 37(2): 159 − 164. (in Chinese) doi: 10.7511/jslx20190121003
[5] 陈莘莘, 钟雅莹, 王崴. 轴对称结构极限下限分析的自然单元法[J]. 力学季刊, 2021, 42(2): 370 − 378. CHEN Shenshen, ZHONG Yaying, WANG Wei. Lower bound limit analysis of axisymmetric structures by natural element method [J]. Chinese Quarterly of Mechanics, 2021, 42(2): 370 − 378. (in Chinese)
[6] 王崴. 轴对称结构极限分析的自然单元法研究[D]. 南昌: 华东交通大学, 2020. WANG Wei. Limit analysis of axisymmetric structures based on the natural element method [D]. Nanchang: East China Jiaotong University, 2020. (in Chinese)
[7] 傅向荣, 陈璞, 孙树立, 等. 弹性力学有限元分析中的平衡与协调理论[J]. 工程力学, 2023, 40(2): 8 − 16. doi: 10.6052/j.issn.1000-4750.2021.08.0647 FU Xiangrong, CHEN Pu, SUN Shuli, et al. Research on equilibrium and conforming theory of the finite element method in elasticity [J]. Engineering Mechanics, 2023, 40(2): 8 − 16. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.08.0647
[8] 龙驭球, 龙志飞, 岑松. 新型有限元论[M]. 北京: 清华大学出版社, 2004. (查阅网上资料, 未找到对应的页码信息, 请确认) . LONG Yuqiu, LONG Zhifei, CEN Song. New developments in finite element method [M]. Beijing: Tsinghua University Press, 2004. (in Chinese) (查阅网上资料, 未找到对应的英文翻译, 请确认) .
[9] CEN S, CHEN X M, FU X R. Quadrilateral membrane element family formulated by the quadrilateral area coordinate method [J]. Computer Methods in Applied Mechanics and Engineering, 2007, 196(41/42/43/44): 4337 − 4353.
[10] 陈万吉, 唐立民. 等参拟协调元[J]. 大连工学院学报, 1981, 20(1): 63 − 74. CHEN Wanji, TANG Limin. Isoparametric quasi-conforming element [J]. Journal of Dalian University of Technology, 1981, 20(1): 63 − 74. (in Chinese)
[11] 李勇东, 陈万吉. 精化不协调平面八节点元[J]. 计算力学学报, 1997, 14(3): 276 − 285. LI Yongdong, CHEN Wanji. Refined nonconforming 8-node plane elements [J]. Chinese Journal of Computational Mechanics, 1997, 14(3): 276 − 285. (in Chinese)
[12] 陈娟, 李崇君, 陈万吉. 四边形单元面积坐标插值的新方法[J]. 工程力学, 2010, 27(5): 45 − 52,67. CHEN Juan, LI Chongjun, CHEN Wanji. A new method of quadrilateral elements by area coordinates interpolation [J]. Engineering Mechanics, 2010, 27(5): 45 − 52,67. (in Chinese)
[13] 陈娟, 李崇君, 陈万吉. 基于面积坐标与B网方法的四边形样条单元[J]. 力学学报, 2010, 42(1): 83 − 92. CHEN Juan, LI Chongjun, CHEN Wanji. Area coordinates and B-net method for quadrilateral spline elements [J]. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(1): 83 − 92. (in Chinese)
[14] 覃霞, 刘珊珊, 吴宇, 等. 平行四边形加肋板自由振动分析的无网格法[J]. 工程力学, 2019, 36(3): 24 − 32,39. doi: 10.6052/j.issn.1000-4750.2018.01.0006 QIN Xia, LIU Shanshan, WU Yu, et al. Free vibration analysis of ribbed skew plates with a meshfree method [J]. Engineering Mechanics, 2019, 36(3): 24 − 32,39. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.01.0006
[15] 陈莘莘, 刁呈岩, 肖树聪. 线弹性断裂力学问题的扩展自然单元法[J]. 工程力学, 2020, 37(7): 1 − 7. doi: 10.6052/j.issn.1000-4750.2019.09.0502 CHEN Shenshen, DIAO Chengyan, XIAO Shucong. An extended natural element method for linear elastic fracture problems [J]. Engineering Mechanics, 2020, 37(7): 1 − 7. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.09.0502
[16] ZENG W, LIU G R. Smoothed finite element methods (S-FEM): an overview and recent developments [J]. Archives of Computational Methods in Engineering, 2018, 25(2): 397 − 435. doi: 10.1007/s11831-016-9202-3
[17] KSHIRSAGAR S, NGUYEN-XUAN H, LIU G R, et al. An SFEM abaqus UEL for nonlinear analysis of solids [J]. International Journal of Computational Methods, 2023, 20(5): 2350003. doi: 10.1142/S0219876223500032
[18] NGUYEN-THOI T, PHUNG-VAN P, THAI-HOANG C, et al. A cell-based smoothed discrete shear gap method (CS-DSG3) using triangular elements for static and free vibration analyses of shell structures [J]. International Journal of Mechanical Sciences, 2013, 74: 32 − 45. doi: 10.1016/j.ijmecsci.2013.04.005
[19] LIU G R, NGUYEN-THOI T, NGUYEN-XUAN H, et al. A node-based smoothed finite element method (NS-FEM) for upper bound solutions to solid mechanics problems [J]. Computers & Structures, 2009, 87(1/2): 14 − 26.
[20] LIU G R, NGUYEN-THOI T, LAM K Y. An edge-based smoothed finite element method (ES-FEM) for static, free and forced vibration analyses of solids [J]. Journal of Sound and Vibration, 2009, 320(4/5): 1100 − 1130.
[21] HE T. Modeling fluid–structure interaction with the edge-based smoothed finite element method [J]. Journal of Computational Physics, 2022, 460: 111171. doi: 10.1016/j.jcp.2022.111171
[22] NGUYEN-THOI T, LIU G R, LAM K Y, et al. A face-based smoothed finite element method (FS-FEM) for 3D linear and geometrically non-linear solid mechanics problems using 4-node tetrahedral elements [J]. International Journal for Numerical Methods in Engineering, 2009, 78(3): 324 − 353. doi: 10.1002/nme.2491
[23] LIU G R. The smoothed finite element method (S-FEM): a framework for the design of numerical models for desired solutions [J]. Frontiers of Structural and Civil Engineering, 2019, 13(2): 456 − 477. doi: 10.1007/s11709-019-0519-5
[24] WAN D T, HU D A, YANG G, et al. A fully smoothed finite element method for analysis of axisymmetric problems [J]. Engineering Analysis with Boundary Elements, 2016, 72: 78 − 88. doi: 10.1016/j.enganabound.2016.08.009
[25] WAN D T, HU D A, NATARAJAN S, et al. A fully smoothed XFEM for analysis of axisymmetric problems with weak discontinuities [J]. International Journal for Numerical Methods in Engineering, 2017, 110(3): 203 − 226. doi: 10.1002/nme.5352
[26] YANG G, HU D A, MA G W, et al. A novel integration scheme for solution of consistent mass matrix in free and forced vibration analysis [J]. Meccanica, 2016, 51(8): 1897 − 1911. doi: 10.1007/s11012-015-0343-5
[27] 张丕辛, 陆明万, 黄克智. 极限分析的无搜索数学规划算法[J]. 力学学报, 1991, 23(4): 433 − 442. ZHANG Pixin, LU Mingwan, HUANG Kezhi. A mathematical programming algorithm for limit analysis [J]. Acta Mechanica Sinica, 1991, 23(4): 433 − 442. (in Chinese)
[28] 胡德安, 韩旭, 万德涛. 有限元方法中的光滑积分伪弱形式[J]. 计算力学学报, 2016, 33(4): 485 − 493. HU Dean, HAN Xu, WAN Detao. A quasi weak form of smoothed integral for finite element method [J]. Chinese Journal of Computational Mechanics, 2016, 33(4): 485 − 493. (in Chinese)
[29] DASGUPTA G. Integration within polygonal finite elements [J]. Journal of Aerospace Engineering, 2003, 16(1): 9 − 18. doi: 10.1061/(ASCE)0893-1321(2003)16:1(9)
[30] 詹世革. 轴对称结构上限分析的数值方法及其应用[D]. 北京: 清华大学, 1995. ZHAN Shige. A numerical method for limit analysis of axisymmetric structures and its application [D]. Beijing: Tsinghua University, 1995. (in Chinese) (查阅网上资料, 未找到对应的英文翻译, 请确认) .
计量
- 文章访问数: 62
- HTML全文浏览量: 5
- PDF下载量: 8
