在偶然灾害性荷载作用下，结构可能因局部破坏而引发与之不成比例的大范围或整体结构的连续性倒塌。该类事故时有发生，并已成为严重威胁公共安全的重要问题^{[1 − 3]}。自20世纪60年代以来，几次重大的连续倒塌事故，如1968年英国Ronan Point公寓、1995年美国A. P. Murrah联邦办公楼、2001年美国纽约世贸双子塔、2013年孟加拉Rana广场和2021年美国迈阿密公寓倒塌事件，引起了学术界和工程界的极大关注、并开展了大量研究，取得了重要研究进展^{[1, 3]}。尽管如此，工程界对于控制连续倒塌的最切合方法尚未形成共识^[3]，相关理论、试验和数值研究均有待进一步深入^{[1 − 2]}。

连续倒塌是结构整体系统的复杂非线性动力行为。试验研究是把握该过程中动力影响的基本手段。例如，肖宇哲等^[4]研究了RC梁柱子结构连续倒塌的动力效应。师燕超等^[5]研究了五层足尺装配式框架结构顶层脚柱失效情形下的动力响应。然而，动力试验研究尚存在诸多困难，如整体上既有静、动力对比试验较少，每次动力试验仅可测得一个性能点等^[2]。鉴于此，数值模拟亦已成为研究结构抗连续倒塌性能的重要途径。例如，甘艺平等^[6]研究了不等跨RC框架的抗连续倒塌性能及定量评判指标。FENG等^[7]验证了基于OpenSees的纤维单元可很好地模拟RC结构抗连续倒塌的相关承载机制，并开展了参数重要性分析。IBRAHIM等^[8]分析了RC框剪结构抗连续倒塌的动力可靠性。限于篇幅，更多相关试验和数值研究可参见相关综述文献[1 − 3]。

拆除构件法常用于RC结构的抗连续倒塌设计^{[3, 9]}。对该类问题进行分析，除直接采用非线性动力法分析结构的动力响应外，非线性静力法因其简单且可较好地反映非线性和大变形下的结构承载机制，也常用于近似求解结构的最大动力响应，并得到了广泛应用^{[3, 9]}。然而，相关研究指出，尽管大量试验表明拟静力试验方法可以在一定程度上把握结构倒塌过程中承载机制的演变，但无法获取实际倒塌可能伴随的动态响应^[2]。实际上，在数值分析中也可能存在同样的问题，如本文研究的RC结构抗连续倒塌承载机制由压拱机制向悬索机制转换过程中，可能存在按静力分析安全而按动力分析不安全的情形。李杰^[10]指出结构静力分析中的失效准则为材料或构件的强度破坏准则，而动力分析中的失效准则一般为整体倒塌或动力失稳准则。周绪红^[11]深入讨论了强度问题和稳定(或变形、刚度)问题之间的关系。事实上，非线性静力下推分析简单实用，但所采用的位移控制方式加载本质上为静力问题，即为准静力平衡过程，对应的失效准则是材料或截面失效^{[10 − 11]}。与之不同，采用力控制加载的动力分析中失效准则一般为动力失稳准则^{[10 − 11]}。

本文以结构稳定理论为基础，首先基于相平面法揭示RC结构的动力跳跃失稳现象，然后研究动力敏感危险域与静、动力失稳之间的关系、分析重要参数对动力敏感危险域的影响规律，最后提出判断结构动力失稳及动力敏感危险域的实用方法。

1   RC结构抗连续倒塌承载机制

RC结构在拆柱后，剩余结构抗连续倒塌承载机制主要包括梁机制、压拱(梁)/压膜(板)机制、悬索(梁)/拉膜(板)机制、空腹机制等^[3]，本文针对与梁相关的承载机制(板类似)加以研究。

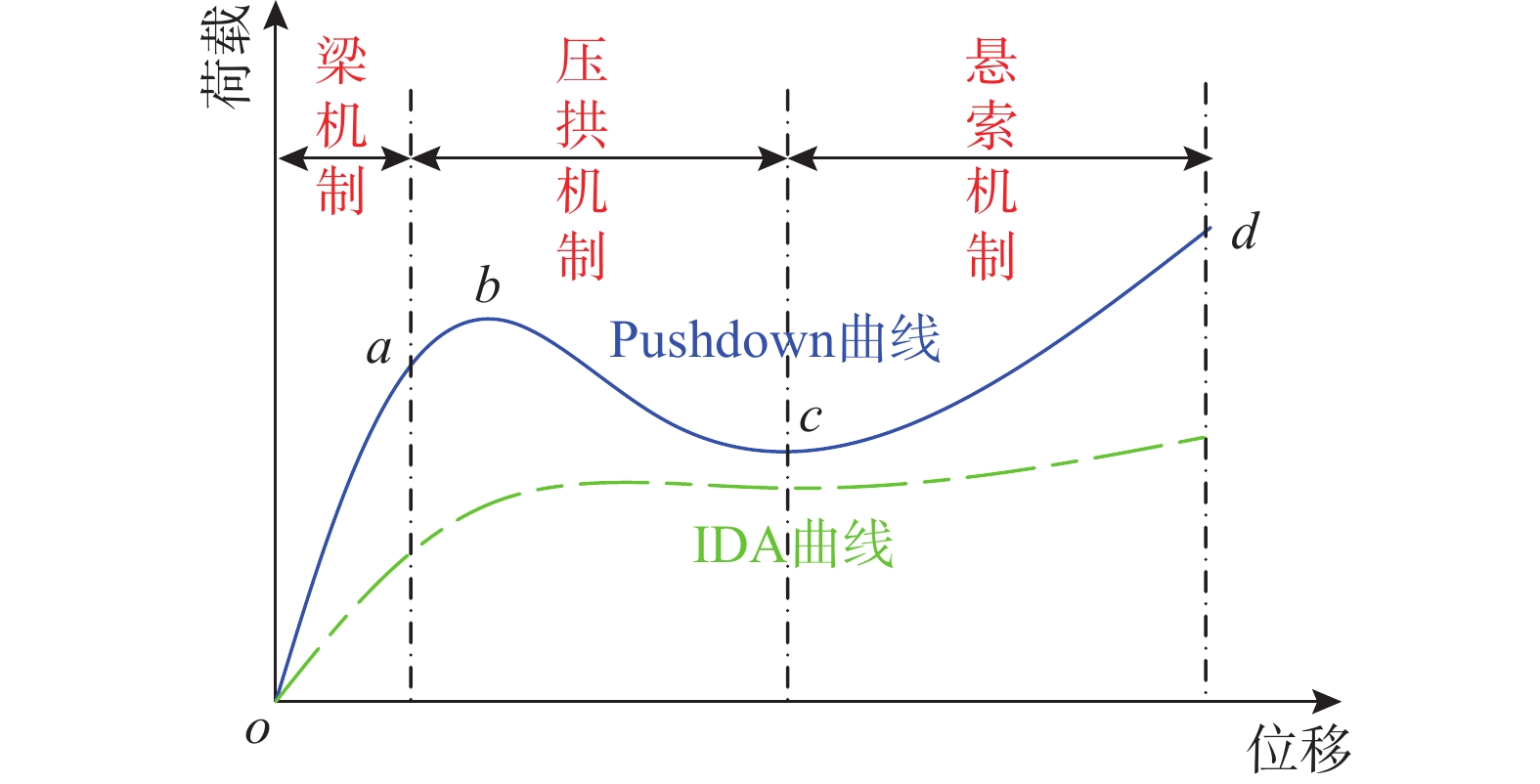
图1给出了拆柱情形下典型的静、动力承载力曲线(由静力下推分析获得Pushdown曲线、增量动力分析获得IDA曲线)及主要承载机制的演变^{[3 − 4]}。实际上，各承载机制之间存在复合与转迁。通常认为先是小变形阶段的压拱机制，被证实可提供稳定可靠的抗连续倒塌强度储备；然后是大变形阶段的悬索机制，常被当作结构抗连续倒塌的最后一道防线，但其性能与配筋情况等诸多因素相关^[9]。

图  1  典型静、动力承载力曲线

Figure  1.  Typical static and dynamic capacity curves

下载: 全尺寸图片 幻灯片

2   动力稳定分析的相平面法

相平面法是研究非线性振动的有效方法之一^[12]。以某单自由度系统自由振动为例，其动力学方程的一般形式为：

式中，x和$\dot x$分别为质点位移和速度。若取：

可得：

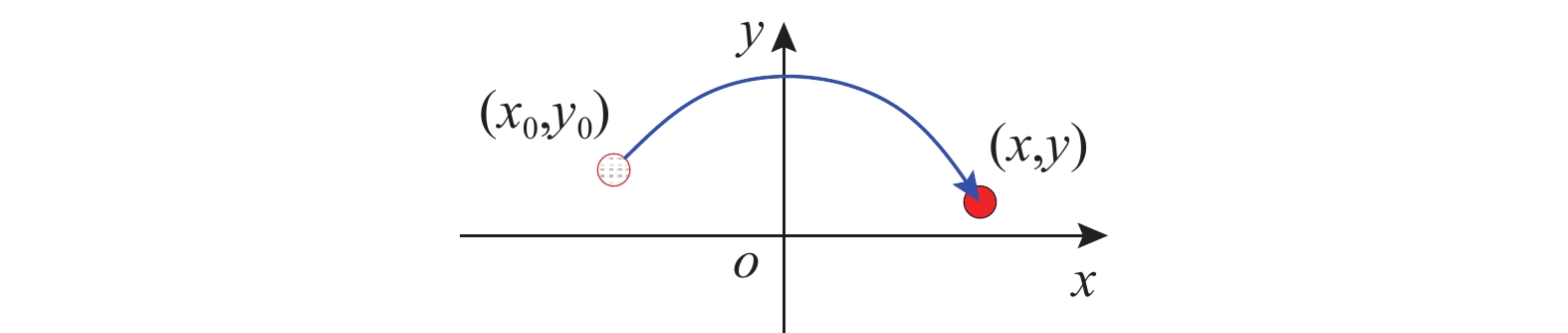
此时，若以x和y为直角坐标建立一个坐标平面Oxy(如图2)，称为系统的相平面，则系统在每一瞬间的运动状态(x，y)对应于相平面Oxy上的一个点(称为相点)。由于相平面上每个不同的点对应于系统的不同状态，因此可用一个动点(相点)在相平面上的运动表示系统运动状态的变化，相点在相平面上运动的轨迹称为相轨迹(如图2)，相平面内不同相轨迹彼此不相交。随着时间推移，在上半平面内(y > 0)相点自左向右移动；下半平面内(y < 0)则自右向左移动；相轨迹在横轴上(y = 0，dy/dx$\to \infty$)与横坐标轴正交。分析系统运动性质的关键在于相轨迹的性状，主要是其运动的方向和特性，而在进行稳定性分析时其定量变化或相点沿相迹运动的定量规律并不十分重要^[12]。因此，相平面法是一种几何或定性方法，可将振动系统一切可能的运动均表示在相平面上，给出系统运动性质的全局“图像”^[12]。

图  2  相平面：相点及相轨迹

Figure  2.  Phase point and phase trajectory in phase plane

下载: 全尺寸图片 幻灯片

相平面内使振动方程式(4)右边分子分母同时为零的特殊点称为相轨迹的奇点^[12]，故奇点都分布在横坐标(y = 0)上。在奇点处，$\dot x = \dot y = 0$表明系统的速度与加速度均为零，其物理意义是系统处于“静”平衡状态，即奇点为平衡点。奇点或系统的平衡状态可以是稳定的也可是不稳定的，如稳定的奇点有稳定焦点和中心，不稳定的奇点有鞍点^[12]。

3   基于相平面法的结构动力稳定性分析

结合现代数值分析与强大算力，相平面法为结构动力稳定性分析提供了有力工具。下面以几个实例说明。

3.1   算例1：弹性两杆桁架

图3(a)所示为一弹性非线性两杆桁架^[13]，该两杆模型由两根相同杆相连组成，可绕支座和交点自由转动，可用于研究某些典型结构系统的失稳特征，如框架、壳体等结构。

图  3  二杆结构系统

Figure  3.  Two-bar truss system

下载: 全尺寸图片 幻灯片

假设结构质量为交点处的集中质量m(单自由度系统)，质点在光滑平面内沿中心线运动方程为：

式中：m为由两杆总质量构成的集中质量，由质量密度ρ=110×10³ kg/m³计算；c为阻尼系数，本文取为零(考虑为保守系统)；f(u)为恢复力-位移函数，由下式决定^[13]：

式中：材料弹性模量E=2.2×10⁵ N/m²；截面积A=0.1 m²；l₀为单杆原始长度(l为变形后长度)，可由半跨长L=1 m与初始位置高度h = 0.5 m确定。图3(b)给出了相应的恢复力-位移曲线。在初始位置处，质点初始速度为零，突然施加给质点以恒定外力F(t) = P。本算例P取为恒定外力，其大小分别考虑为300 N、600 N和1000 N共三个工况。

图4给出了位移时程曲线和相轨迹曲线。图4(a)为300 N作用下的位移时程曲线，峰值位移小于图3(b)中1点处的位移，此时的运动为在0和1之间、以a为平衡位置(奇点)的往复周期运动，理论分析可知结构未发生失稳。图4(b)为300 N工况下的相轨迹(速度-位移)曲线，表现为由左向右、自上到下的极限环(周期运动)^[12]，与位移时程曲线上相应的特征点已采用相同符号标出。该极限环有且仅有一个中心(奇点中的稳定平衡点)^[12]，仅在与中心点对应的最高和最低两处相轨迹切线斜率为零或加速度为零，即为平衡点，相轨迹的性状在运动过程中未发生改变，即结构未发生动力失稳。

图4(c)为600 N工况下的位移时程曲线，此时结构以图3(b)中b、c和d三处为平衡位置做周期往复运动，最大位移超过了1点和2点处的位移，从理论分析可知这时存在动力失稳。与300 N工况相比，虽相轨迹仍为极限环(周期运动)，但奇点(平衡点)由一处增为三处，即图4(d)相轨迹图中自左至右的中心、鞍点(不稳定平衡点)^[12]和中心，分别对应图3(b)中的b、c和d三处。奇点处对应的相轨迹切线斜率为零，即加速度为零的平衡点。因存在鞍点，改变了相轨迹的性状，结构系统发生了动力跳跃失稳。

图4(e)和图4(f)分别给出了1000 N工况下的位移时程和相轨迹曲线。此时，结构以图3(b)中e处为平衡位置做周期往复运动，从理论分析可知二杆模型未发生失稳。图4(f)中相轨迹为单中心的极限环，与300 N工况类似，相轨迹切线斜率或加速为零仅中心点一处。此时，因仅有一处稳定平衡位置，且不存在鞍点，未出现600 N工况时的动力跳跃失稳。

图  4  位移响应时程曲线与相轨迹

Figure  4.  Time-history responses of displacement and phase trajectory

下载: 全尺寸图片 幻灯片

综上，可通过相平面法直观地判断结构是否发生动力失稳。相轨迹的性状(如奇点个数和类型)不发生改变则动力运动稳定，否则发生动力失稳且存在鞍点，注意此时不涉及结构破坏的情形。

3.2   算例2：RC梁柱子结构

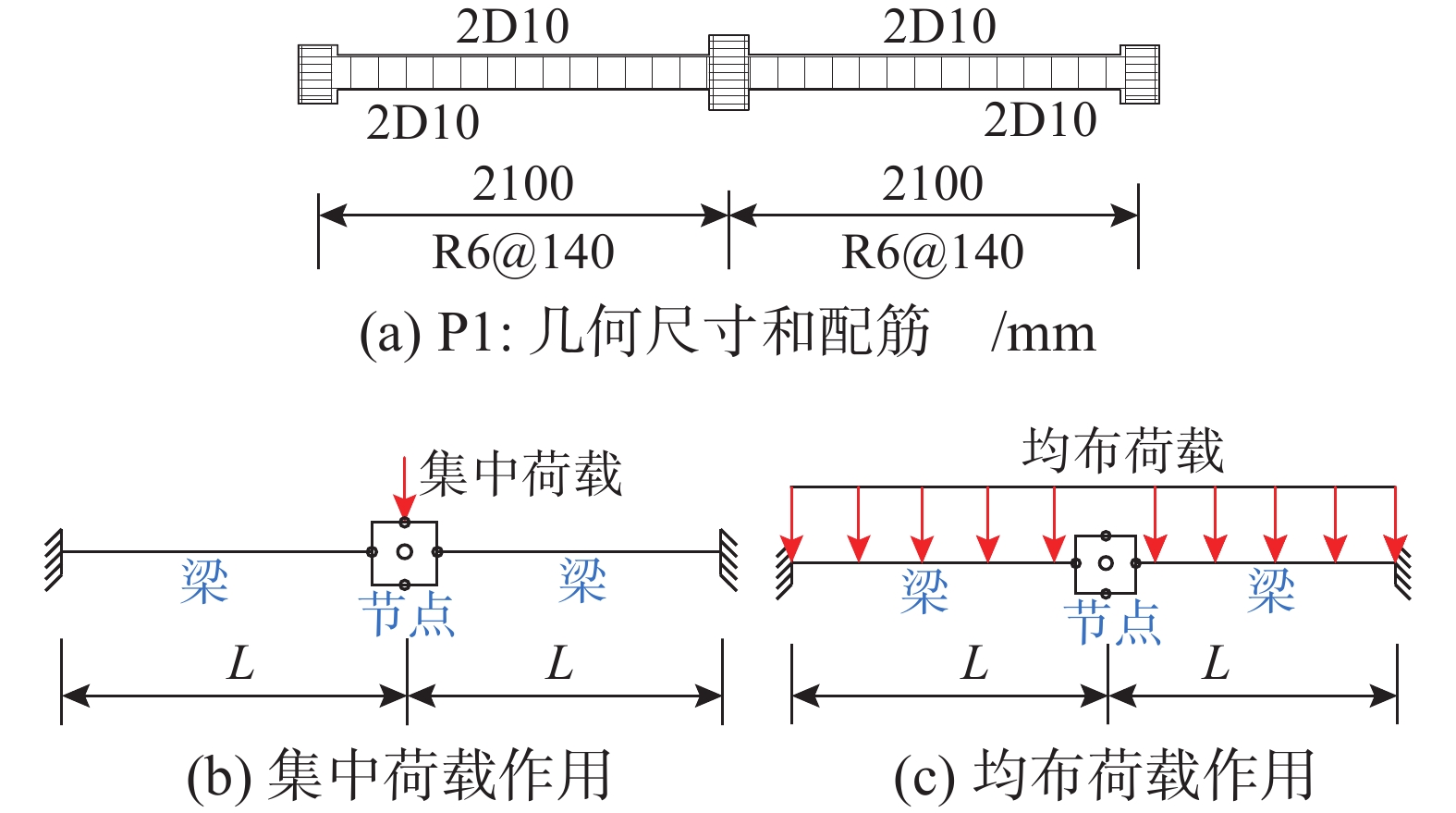
以QIAN等^[14]试验中的RC梁柱子结构P1为例，采用相平面法识别连续倒塌中的动力失稳。平面双跨梁柱子结构P1的截面尺寸和配筋信息如图5(a)，混凝土抗压强度为19.9 MPa，纵向钢筋屈服强度为437 MPa、抗拉强度为568 MPa。试验中将边柱固定，通过位移加载方式在中柱柱顶采用竖向集中荷载加载，即静力下推(Pushdown)分析，记录中柱处的荷载-位移曲线，即图6(a)中的曲线“Exp”。

采用开源有限元分析软件OpenSees^[15]建立P1的有限元模型。其中，采用Force-based纤维单元模拟梁，每个单元设置5个积分点。采用Joint2D单元模拟中柱节点，并采用修正压力场模型^[7]确定剪应力-剪应变关系；未考虑边柱节点，设为固定约束，如图5(b)。选用Co-rotational transformation考虑几何非线性。混凝土和钢筋分别采用ConcreteD和Hysteretic材料本构模型。更多详情参见文献[7, 15]。

图  5  RC梁柱子结构

Figure  5.  RC beam-column substructure

下载: 全尺寸图片 幻灯片

首先，与试验保持一致，采用位移控制方式进行竖向集中荷载加载(图5(b))。图6(a)对比了中柱处荷载-位移曲线的模拟结果(Pushdown曲线)与试验结果(Exp曲线)，虽第一个峰值(压拱效应)处二者误差为9%，但两者整体变化趋势完全一致。

进一步，采用增量动力分析(IDA)方法^[9]计算动力拆柱下结构的动力响应。每次动力时程分析中，首先在中柱底部设置竖向位移约束，然后施加集中荷载至平衡态，最后突然释放前述竖向约束以模拟动力拆柱情形并记录中柱处位移和速度时程。采用Rayleigh阻尼模型^[9]，并设定阻尼比为5%。图6(b)为IDA分析所得中柱处位移时程曲线，竖向位移首先单调增加，然后在平衡位置处往复振动，并因阻尼耗能导致振动幅值不断衰减，荷载越大其竖向位移越大，动力极限承载力为38.715 kN(采用0.005 kN分辨率)。同时，发现荷载由31.5 kN增至32 kN的过程中，竖向位移响应显著增大，且达到峰值位移所需时间较前后时程响应显著增长。这与正常现象不一致，因在该区域发生了动力跳跃失稳，接下来由相平面法识别该动力跳跃失稳。

图6(c)和图6(d)给出了图6(b)中各荷载工况对应的相轨迹，新增加了速度相的信息。图6(c)为5 kN~31.5 kN对应的相轨迹，因阻尼耗能系统为非保守系统，故每条相轨迹收敛于稳定焦点^[12]。此时，每条相轨迹每半圈上(半个振动周期)仅存在一处切线斜率或加速度为零的平衡点，结构未发生动力失稳，这与算例1中保守系统300 N对应的单中心极限环类似。图6(d)为31.5 kN~38.72 kN对应的相轨迹，在32 kN的相轨迹中首次出现了鞍点，其相轨迹的首个半圈上存在三处切线斜率或加速度为零的平衡点。其中，相轨迹上第二处切线斜率为零处对应为鞍点，改变了相轨迹的性状，结构发生了动力失稳，但并未发生倒塌破坏。在某种程度上，这与算例1中600 N对应的存在鞍点的极限环类似，奇点个数增加且出现了鞍点。后续相轨迹上均存在鞍点而存在动力失稳，直至38.72 kN结构发生倒塌破坏，其相轨迹再次出现鞍点且后续不断发散。尽管如此，相轨迹出现鞍点仅代表结构发生了动力失稳，而判断结构是否发生破坏或倒塌还需结合相关失效判据综合分析。

图  6  集中荷载作用结果

Figure  6.  Results of concentrated loading

下载: 全尺寸图片 幻灯片

在上述有限元模型基础上，改为施加更符合实际情况的梁上均布线荷载，见图5(c)，分别开展Pushdown分析和IDA分析。图7(a)~图7(c)分别为中柱处的Pushdown曲线与IDA-5%曲线、位移时程曲线和相轨迹。与图6中集中荷载结果不同之处为此时未发生动力跳跃失稳。图7(b)中的位移时程曲线的峰值响应及所需时间均随荷载增加而单调增加。除在15.32 kN/m荷载作用下因发生破坏而出现鞍点外，图7(c)中其他相轨迹的性状均未发生改变，仅存在一个奇点且收敛于稳定焦点，验证了在此情况下结构未发生动力失稳。同样，此处需说明，结构倒塌工况15.32 kN/m时出现鞍点仅说明了结构出现了动力失稳。因其相轨迹不断发散至最大变形超过了结构跨度，结构明显已发生了倒塌破坏。

图  7  均布荷载作用结果

Figure  7.  Results of uniformly distributed loading

下载: 全尺寸图片 幻灯片

3.3   算例3：RC平面框架结构

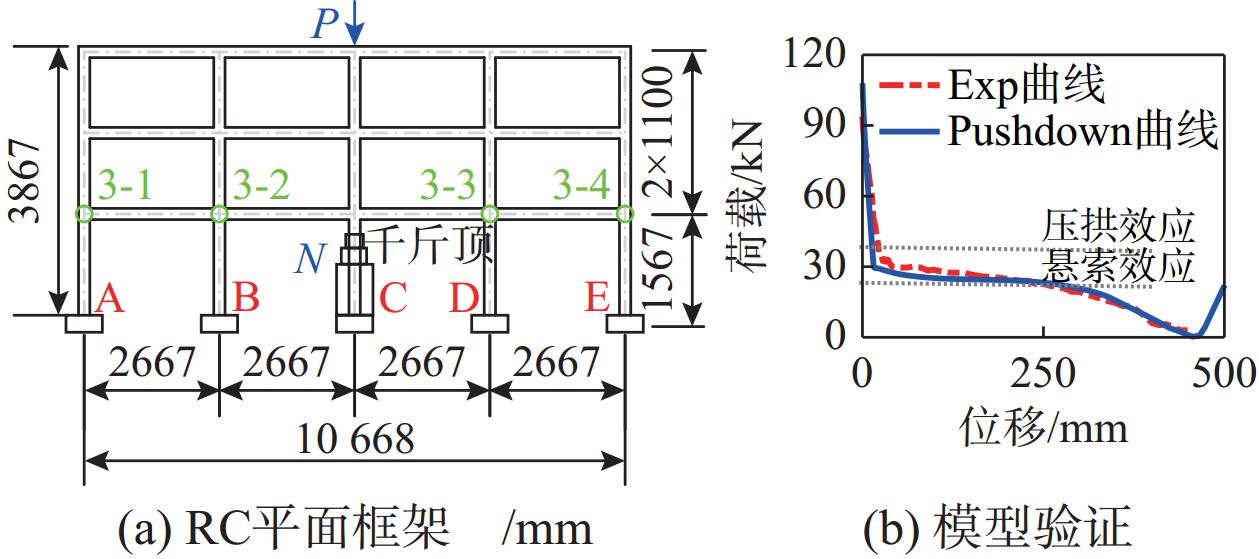
YI等^[16]对1/3缩尺的三层四跨RC平面框架开展了连续倒塌试验研究，试验布置如图8(a)。试验中，在第三层柱顶施加竖向集中荷载P，采用千斤顶逐渐卸载方式模拟底层中柱的失效并记录轴向力N，图8(b)给出了试验记录轴向力N与底层中柱顶点处竖向位移曲线“Exp”。采用OpenSees建立框架的有限元模型(参见3.2节)，相关几何和材料参数与试验保持一致，详见参考文献[16]。图8(b)对比了试验结果和模拟结果，两者吻合良好，模拟所得压拱机制和悬索机制也与试验相同。

图  8  RC平面框架

Figure  8.  RC planar frame

下载: 全尺寸图片 幻灯片

分别开展Pushdown分析和IDA分析，图9(a)~图9(c)分别为底层中柱柱顶处的Pushdown与IDA-5%曲线、位移时程曲线和相轨迹。通常因存在动力效应，动力承载曲线应在静力承载力曲线下方，否则会导致动力失稳^[17]。图9(a)中静、动力承载力曲线在200 mm~300 mm区域十分接近，实际上存在短暂动力跳跃失稳，表现为图9(b)中该位移区间的动力响应振动效应较弱、达到峰值响应所需时间为所有响应中最长。该现象与稳定性分析所采用动力法^[11]的基本原理一致，即结构在临界失稳荷载处的振动效应趋近于零、振动周期趋于无穷大。图9(c)和图9(d)中的85 kN荷载对应相轨迹亦验证了短暂动力跳跃失稳的存在，相轨迹首个半圈上存在三处位置对应的相轨迹切线斜率或加速度为零，其中第二处为鞍点，相平面法精准地识别出了该轻微的动力失稳行为。此外，除倒塌破坏工况90.06 kN外，图中其他工况均未发生动力失稳行为。

图  9  平面框架分析结果

Figure  9.  Results for the RC planar frame

下载: 全尺寸图片 幻灯片

4   RC结构抗连续倒塌承载机制的动力敏感危险域分析

4.1   动力敏感危险域

针对前述图6(b)、图7(b)和图9(b)中IDA位移时程的峰值响应与相应荷载分别画于图6(a)(情形I：RC子结构-集中荷载)、图7(a)(情形II：RC子结构-均布荷载)和图9(a)(情形III：RC框架-集中荷载)中，即动力承载力曲线或IDA-5%曲线。对比静、动力承载力曲线，即Pushdown与IDA-5%曲线，其中情形I与情形III情况基本相同，静、动力工况下结构的极限变形能力大致相同。然而，情形II与前述二者差异显著，动力承载力曲线的变形能力显著小于静力承载力曲线，两者延性差异巨大。此时，若仅采用静力分析将过度高估结构的变形能力，而在动力情形下结构远达不到该变形水平。

本文称该现象为动力敏感危险域，在此域内结构按静力分析安全而按动力分析不安全，即对动力效应敏感。同时，由于动力工况下的变形能力远小于静力工况下的变形能力(如情形II中分别位于小变形阶段的压拱机制和大变形阶段的悬索机制)，动力情形下达不到按静力工况设计的变形能力，更易于发生脆性破坏，而非延性破坏模式，这在工程实际中是十分危险的。究其原因，主要为静、动力失效准则存在差异，分别为材料或截面破坏准则(强度问题)和动力倒塌或失稳准则(变形问题)^{[10 − 11]}。静力分析中采用位移控制方式加载，而动力分析中采用力控制方式加载，正是对偶地分别对应于前述两种失效准则。

动力敏感危险域的产生既与静、动力失效准则(或静、动力失稳)存在差异有关，也与结构抗连续倒塌承载机制相关。例如，情形II(图7(a))中Pushdown曲线上第一(压拱机制)和第二(悬索机制)处峰值荷载分别为17.4 kN/m和17.9 kN/m，后者仅略微大于前者，整体静力承载力为后者。此时，静、动力分析结果变形能力差异显著，在该区域出现了动力敏感危险域。若Pushdown曲线上第二峰值显著大于第一峰值，如情形I和III，结构虽会发生短暂动力失稳，但一般仍能稳定于新的平衡位置，静、动力失稳都将恢复，二者此时变形能力大致相当，无动力敏感危险域。若后者小于前者，则将同时发生静、动力失稳。

4.2   参数分析

本小节进一步研究压拱机制和悬索机制的相对强弱关系与动力敏感危险域的关系。实际上，抗连续倒塌承载机制与诸多因素相关，如材料性能、几何尺寸、构造措施和边界条件等^{[18 − 20]}。为简化问题的复杂性，本文仅通过控制变量法的思想，分析对悬索机制影响显著的相关参数对动力敏感危险域的影响规律。在大变形阶段，若混凝土完全退出工作且梁中所有钢筋充分受拉(材料被充分利用)时，悬索机制提供的理论极限承载力(如图5(b)跨中集中外荷载为例)和梁中轴力分别为：

式中：P为跨中集中外荷载；N_B为梁中轴力；α为梁中轴力与水平轴夹角；n为梁中钢筋根数；f_u为钢筋极限强度；A为单根钢筋横截面面积。

考虑钢筋本构关系为双线性模型：

式中：E_s为钢筋弹模；ε、ε_y和ε_u分别为钢筋应变、屈服和极限应变；f_y为屈服强度；b₀为硬化率。若保持b₀相同，式(9)中钢筋极限强度则由极限应变确定。式(8)中，钢筋直径D直接决定钢筋面积A。因此，选择钢筋极限应变ε_u和直径D两个最重要变量进行参数分析，这与FENG等^[7]对悬索效应相关参数重要性分析结果一致。

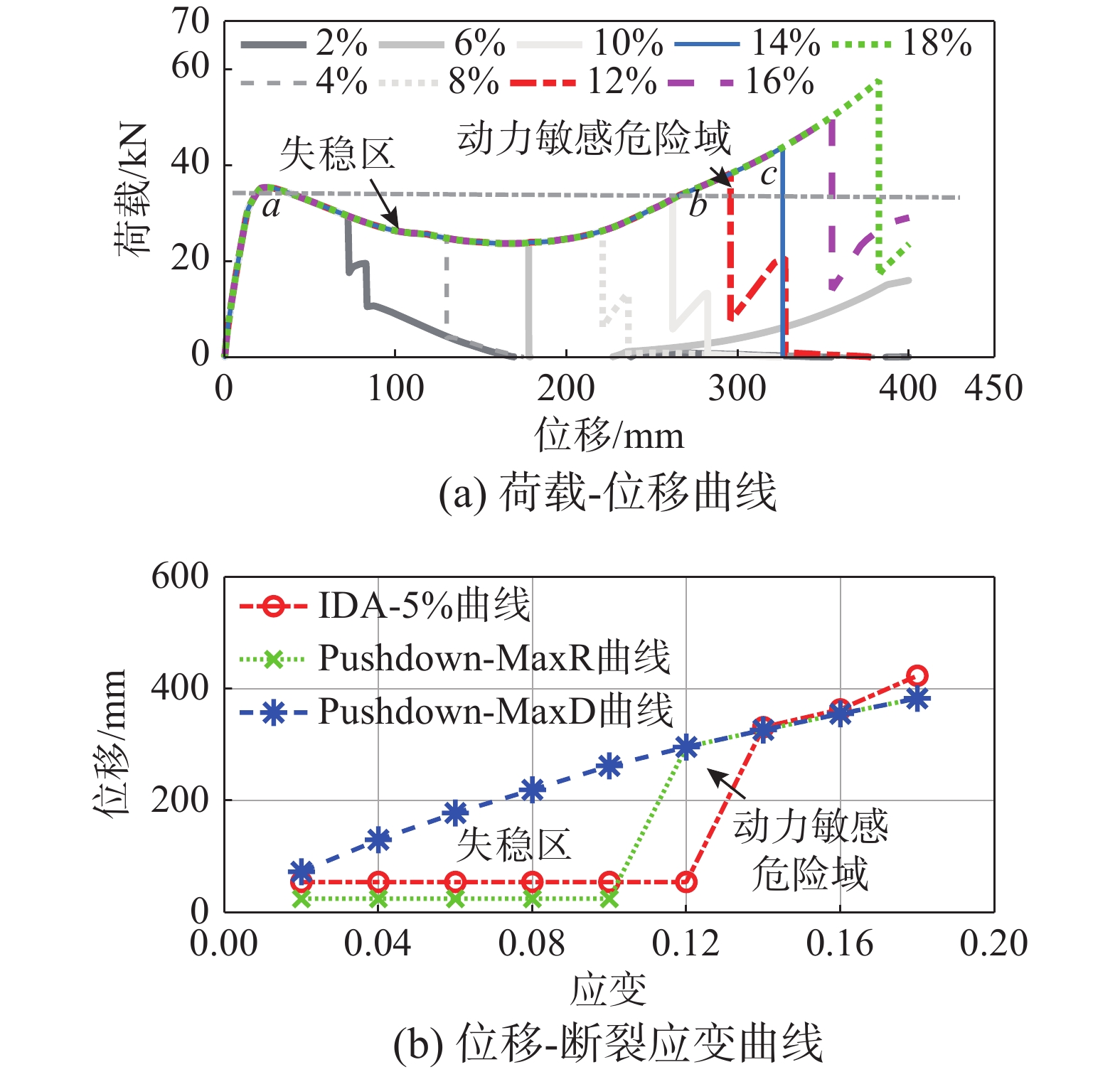
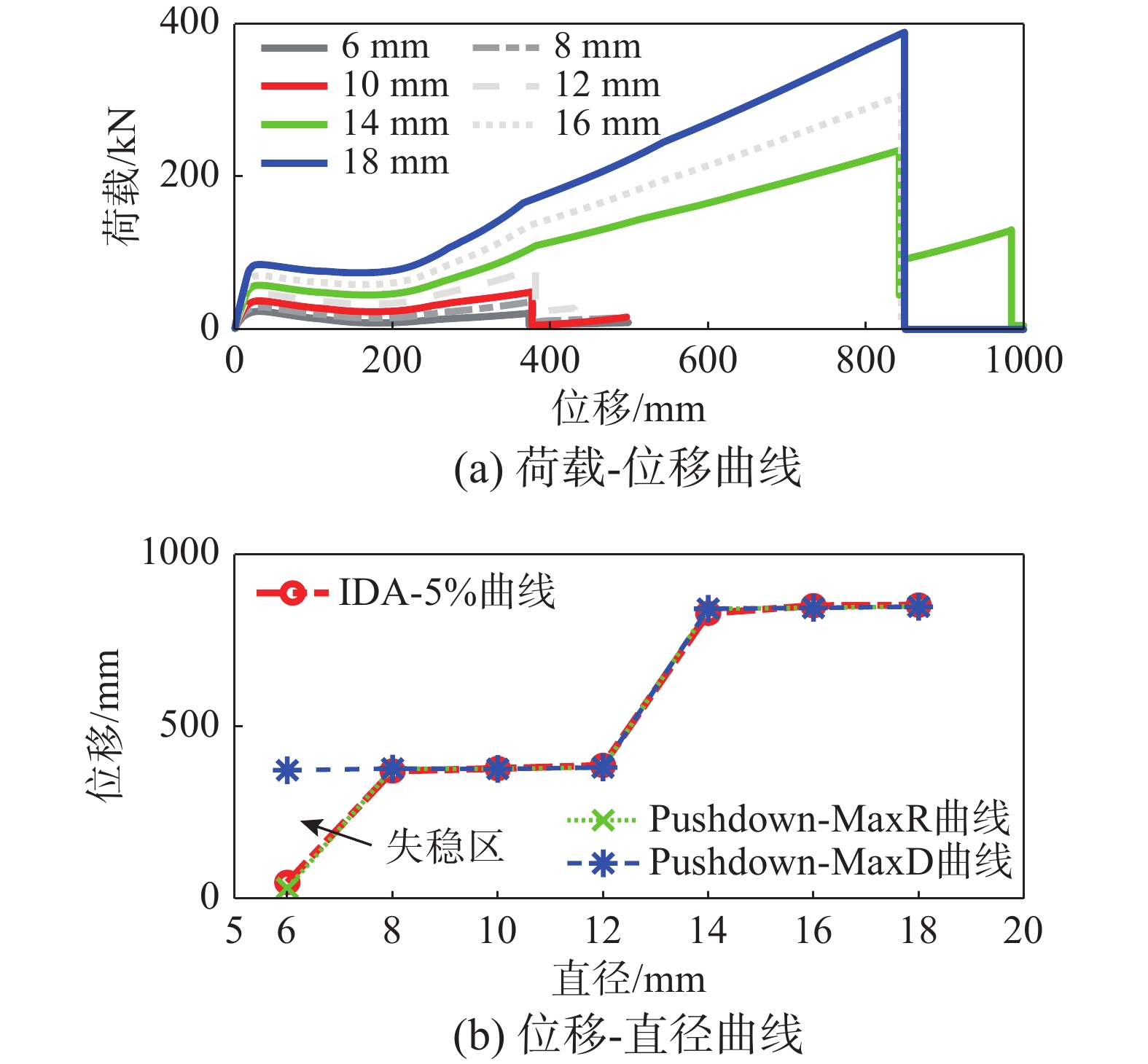
以算例2中集中荷载作用下梁柱子结构为对象(图5(b))，即情形I，首先分析钢筋极限应变ε_u对动力敏感危险域的影响规律，ε_u分别设定为2%、4%、6%、8%、10%、12%、14%、16%和18%，保持其他参数不变，分别开展Pushdown和IDA分析。图10(a)给出了不同ε_u下的Pushdown曲线，所有曲线第一个承载力峰值a点均相同，但变形能力Pushdown-MaxD随着ε_u增大而增大。在b点之前(当ε_u介于10%与12%)的工况均为静力峰值(压拱机制)后极值点失稳^[11]；但b点之后情况发生改变，曲线上全局最大承载力转移至第二个峰值(悬索机制)处，对应的全局最大承载力处位移Pushdown-MaxR见图10(b)。若Pushdown-MaxR与Pushdown-MaxD曲线不重合，则结构在承载机制转换过程中发生静力极值点失稳。

图  10  集中荷载：钢筋断裂应变

Figure  10.  Concentrated loading: rebar ultimate strain

下载: 全尺寸图片 幻灯片

图11给出了IDA和Pushdown曲线。图11(a)中，ε_u不超过10%时的IDA曲线均相同，且在IDA曲线与Pushdown曲线交点处发生了动力失稳倒塌破坏。动力极限变形大于静力承载力处的变形Pushdown-MaxR(图10(b))，即静、动力失稳对应的承载力与变形能力均不一致，两者并不同步。图11(b)给出了ε_u=12%时的静、动力承载力曲线，IDA曲线与之前相同，仍在较小位移处产生了动力失稳倒塌，但Pushdown曲线上的全局承载力由第一个峰值转移至第二个峰值处，此时两者的变形能力相差显著(图10(b))，若仅按静力情形分析设计，可能实际动力响应过程中达不到预期的变形能力，存在倒塌风险。图11(c)所示为ε_u=14%时的承载力曲线，因动力跳跃失稳后能稳定于新的平衡位置，可由图11(d)中的相轨迹验证，此时静、动力变形能力基本相同。

综上，静、动力失稳存在差异且并未协同；当仅有动力失稳而静力失稳已恢复时，存在动力敏感危险域，且为失稳区的子集，如图10中ε_u=12%附近为动力敏感危险域。

图  11  集中荷载：静、动力失稳

Figure  11.  Concentrated loading: static and dynamic instability

下载: 全尺寸图片 幻灯片

图12给出了对钢筋直径进行参数分析的结果。图12(a)为钢筋直径分别为6 mm、8 mm、10 mm、12 mm、14 mm、16 mm和18 mm工况下的Pushdown曲线。钢筋直径为6 mm时，全局承载力为第一个峰值，发生了静、动力失稳，见图12(b)。自8 mm始，全局承载力为第二峰值处，未出现动力敏感危险域。理论上，该区间存在动力敏感危险域，但因钢筋直径为确定的离散值，故仅观察到了失稳区。需特别注意的是，图12(a)中钢筋直径14 mm、16 mm和18 mm工况下对应的变形能力和极限承载力均远大于其他工况，出现该现象的原因为前者更充分地利用了钢筋的材料性能，梁中上下两层钢筋的抗拉能力被充分地利用，避免了后者中一层钢筋先于另一层钢筋过早断裂的情况或材料未最优利用，即出现了多失效模式，对此可进一步研究，这里不再赘述。不失一般性，进一步考察均布荷载作用下(图5(c))，钢筋极限应变和直径变化与动力敏感危险域的关系，结果分别如图13和图14。图13(a)和图14(a)为Pushdown曲线，其规律与集中荷载情形相似。图13(b)和图14(b)给出了失稳区和动力敏感危险域，可得出相同的结论，且动力敏感危险域更显著。

图  12  集中荷载：钢筋直径

Figure  12.  Concentrated loading: rebar diameter

下载: 全尺寸图片 幻灯片

图  13  均布荷载：钢筋断裂应变

Figure  13.  Uniformly distributed loading: rebar ultimate strain

下载: 全尺寸图片 幻灯片

图  14  均布荷载：钢筋直径

Figure  14.  Uniformly distributed loading: rebar diameter

下载: 全尺寸图片 幻灯片

5   动力失稳与动力敏感危险域近似判定方法

前文采用IDA方法分析了结构动力失稳及动力敏感危险域，本小节进一步研究基于能量法计算的伪静力承载力曲线或EBM曲线，以实现快速近似地判断是否存在动力失稳及动力敏感危险域。

前述分析中，结构动力承载力曲线由IDA分析所得。除此之外，可根据能量守恒原理，由Pushdown曲线近似计算最大动力响应或伪静力曲线，该方法已广泛应用于连续倒塌动力分析之中^{[9, 21 − 23]}。针对算例2中的集中荷载作用情形(图5(b))或情形I，图6(a)也给出了由能量法计算的伪静力EBM曲线和取阻尼比为零进行IDA分析所得IDA-0%曲线。EBM曲线为双峰值曲线，而IDA-0%曲线为单峰值，但IDA-0%上的点均落在了EBM曲线上，验证了EBM方法的有效性。同时，EBM曲线和IDA-0%曲线都低于IDA-5%曲线，因为EBM在换算过程中未考虑阻尼效应耗能。Pushdown曲线为双峰值曲线，在A点发生静力失稳、在B点恢复静力失稳，随后继续增加至最大承载力后出现破坏下降段。IDA-0%曲线在a点首次超越Pushdown曲线时发生了动力跳跃失稳，随后在b点恢复动力稳定并继续上升，最后在超越Pushdown曲线达到最大值后发生动力失稳倒塌破坏。IDA-5%曲线在31.5 kN处首次超越Pushdown曲线发生动力跳跃失稳、在32 kN处恢复动力失稳，随后单调递增超过Pushdown曲线后发生动力失稳倒塌破坏。

针对算例2中的均布荷载作用情形(图5(c))或情形II，图7(a)也给出了由能量法计算的EBM曲线和IDA-0%曲线。同样，EBM曲线与IDA-0%曲线吻合良好，EBM曲线和IDA-0%曲线都低于IDA-5%曲线。然而，虽然EBM曲线也为双峰值曲线，但第二峰值点b小于第一峰值点a，即在a点首次超越Pushdown曲线时发生了动力失稳倒塌破坏。IDA-0%曲线也在a点首次超越Pushdown曲线时发生了动力失稳倒塌破坏。IDA-5%曲线也在15.315 kN/m首次超越Pushdown曲线时发生了动力失稳倒塌破坏。Pushdown曲线也为双峰值曲线，在A点发生静力失稳、但在B点恢复静力失稳，随后继续增加至达到静力承载力峰值17.9 kN/m。

针对算例3中的集中荷载作用情形(图8(a))或情形III，图9(a)给出了由能量法计算的EBM曲线和IDA-0%曲线。同样，EBM曲线与IDA-0%曲线都为单峰值曲线且二者吻合良好，都随位移单调递增至峰值点a，并在a点首次超越Pushdown曲线时发生了动力失稳倒塌破坏。EBM曲线和IDA-0%曲线都低于IDA-5%曲线，IDA-5%曲线也单调递增至首次超越Pushdown曲线时发生了动力失稳倒塌破坏。Pushdown曲线此时也为单峰值曲线，即先单调递增至静力承载峰值，随后因损伤累积而出现下降段直至倒塌破坏。

综上，可通过IDA曲线或EBM曲线在相同位移处超越Pushdown曲线作为近似判定结构发生动力跳跃失稳或动力失稳倒塌破坏的判据。IDA曲线或EBM曲线最后一次超越Pushdown曲线时，对应动力失稳倒塌破坏；其他情况出现超越情形，则为发生动力跳跃失稳。该判据的理论依据如下，由式(5)中的运动平衡方程等号两边同时对位移进行积分，可得能量平衡方程：

式中，E_K、E_D、E_S和E_W分别为结构系统的动能、阻尼耗能、应变能和外力做功。此外，Pushdown曲线对位移积分所得面积为结构的应变能E_S，IDA曲线上任意点处动能E_K = 0。IDA-0%和EBM曲线不考虑阻尼效应，即E_D = 0；若E_W > E_S，则结构不能满足能量平衡方程而发生动力失稳，即E_K不为零。IDA-5%曲线考虑阻尼效应，若E_W − E_S > E_D，结构亦不能满足能量平衡方程，将发生动力失稳，E_K为非零值。例如，在情形III中Pushdown曲线与IDA-5%曲线无交点但仍发生了动力失稳，即为该情形，则不能采用该判据。需采用相平面法，如情形III中精准地识别出了在85 kN工况时发生了轻微动力跳跃失稳。因此，特别指出采用该判据的前提条件为静、动力承载力曲线需存在交点。

当EBM曲线为双峰值曲线时，可判断结构存在动力敏感危险域，包括以下两种情况：EBM曲线第二峰值承载力大于第一峰值处的承载力，发生动力跳跃失稳，因静力失稳恢复而动力失稳尚未恢复，导致出现动力敏感危险域，例如情形I；EBM曲线第二峰值承载力小于第一峰值处的承载力、且Pushdown曲线静力失稳已恢复，虽然直接发生动力失稳倒塌破坏，但同样因静力失稳恢复而动力失稳无法恢复而导致动力敏感危险域，例如情形II。

6   结论

本文通过数值模拟，以结构稳定分析理论为基础，基于相平面方法揭示了RC结构抗连续倒塌的动力敏感危险域，研究了结构连续倒塌相关相轨迹的特征，提出了快速近似判断动力失稳及动力敏感危险域的简便方法，得到以下结论：

(1) 结构抗连续倒塌承载机制由压拱机制转换到悬索机制的阶段，可能存在静、动力失稳，且两者可能不协同，二者可能同时出现也可能仅出现动力跳跃失稳。

(2) 动力跳跃失稳可由相平面法直观地分析。相轨迹性状不发生改变且收敛于中心点(保守系统)或稳定焦点(耗散系统)时，无动力失稳。相轨迹上存在鞍点或发散，则结构发生动力失稳。

(3) 当Pushdown曲线上全局承载力刚由压拱机制转移至悬索机制时，可能存在动力敏感危险域。此时，静力失稳恢复，动力失稳仍存在，动力极限变形能力远小于静力极限变形能力。

(4) 若动力承载力曲线与静力承载力曲线存在交点，在前者超越后者时，结构将因不满足动能为零的条件而发生动力失稳。

(5) 若Pushdown曲线为双峰值曲线且第二峰值为最大值，同时由能量法换算的伪静力曲线也为双峰值，则存在动力敏感危险域。