考虑地震动空间相关性的区域群体建筑直接经济损失评估

丁佳伟; 吕大刚; 曹正罡

doi:10.6052/j.issn.1000-4750.2023.09.0646

考虑地震动空间相关性的区域群体建筑直接经济损失评估

丁佳伟^{1, 2,},
吕大刚^{1, 2, ,},
曹正罡^{1, 2,}

1.
哈尔滨工业大学，结构工程灾变与控制教育部重点实验室，黑龙江，哈尔滨 150090
2.
哈尔滨工业大学，土木工程学院智能防灾减灾工业与信息化部重点实验室，黑龙江，哈尔滨 150090

基金项目: 国家重点研发计划项目(2021YFB2600500)；国家自然科学基金项目(52078176，52278167)

详细信息

作者简介:
丁佳伟(1995−)，男，山东人，博士生，主要从事强地面运动模拟、地震动物理模型与工程结构抗震研究(E-mail: dingjw1995@163.com)

曹正罡(1975−)，男，黑龙江人，教授，博士，博导，主要从事大跨空间结构与地震工程以及轻钢结构方面的研究(E-mail: caohit@hit.edu.cn)

通讯作者:
吕大刚(1970−)，男，黑龙江人，教授，博士，博导，主要从事土木工程安全、风险与韧性研究(E-mail: ludagang@hit.edu.cn)

中图分类号: TU375.4；P315.9
计量
- 文章访问数: 63
- HTML全文浏览量: 19
- PDF下载量: 15
出版历程
- 收稿日期: 2023-08-31
- 修回日期: 2024-01-15
- 网络出版日期: 2024-03-28

DIRECT ECONOMIC LOSS ESTIMATION FOR REGIONAL PORTFOLIO BUILDINGS CONSIDERING SPATIAL CORRELATION OF GROUND MOTIONS

DING Jia-wei^{1, 2,},
LYU Da-gang^{1, 2, ,},
CAO Zheng-gang^{1, 2,}

1.
Key Lab of Structure Dynamic Behavior and Control of China Ministry of Education, Harbin Institute of Technology, Harbin, Heilongjiang 150090, China
2.
Key Lab of Smart Prevention and Mitigation of Civil Engineering Disaster of the Ministry of Industry and Information Technology, Harbin Institute of Technology, Harbin, Heilongjiang 150090, China

摘要

摘要:
基于空间相关随机场的区域地震风险量化，需要对所有感兴趣地点的地震动强度进行联合分布建模，因此评估地面运动的空间相关性是在区域尺度上评估地震损失评估的第一步。区域群体建筑结构的数量、种类以及分布的随机性、复杂性对震前预测和震后评估都具有重要影响。该文提出了考虑地震动空间相关性和建筑结构空间分布不确定性的区域群体建筑概率损失评估框架，基于地统计学方法表征地震动强度参数(IMs)的空间相关性，采用“双层蒙特卡洛法”随机模拟地震动空间相关性影响场和区域群体建筑结构的空间分布，实现快速、高效和准确的区域地震损失评估。以一个50 km×50 km的区域为例，假定区域中心发生M_w7.2级地震情景，分别以不同的损失比为基础计算了考虑空间相关性与不考虑空间相关性以及区域建筑结构固定空间分布与随机空间分布情况下的地震直接经济损失，结果表明：考虑地震动空间相关性对区域地震直接经济损失的评估精度具有重要的影响，在考虑空间相关性的情况下，区域群体建筑结构直接经济损失的蒙特卡洛模拟统计结果呈对数正态分布，损失年超越概率在中、高直接经济损失处将明显大于未考虑空间相关性的损失年超越概率。
- 区域群体建筑 /
- 概率损失评估 /
- 直接经济损失 /
- 空间相关性 /
- 地统计学
Abstract:
Regional seismic risk quantification based on a spatial correlation random field requires the modeling of joint distributions of ground motion intensity measures at all interested sites. Therefore, the assessment of spatial correlation of ground motion is the first step to assess seismic loss at a regional scale. The quantity, type and distribution randomness and complexity of regional portfolio buildings have an important impact on pre-earthquake prediction and post-earthquake rapid assessment. This study introduces the basic theory for spatial correlation of seismic intensity parameters (IMs) using geo-statistics and the method for randomly generating a regional spatial correlation influence field using Monte Carlo simulation. A rapid loss assessment framework considering the randomness of spatial distribution of portfolio building structures is proposed. The framework uses “double-loop Monte Carlo random simulation” to simulate the spatial correlation influence field of ground motions and the spatial distribution of regional portfolio building structures, it realizes as a kind of rapid, efficient and accurate regional modeling and loss assessment. At last, taking 50 km ×50 km area as an example and, assuming that an earthquake event with Mw=7.2 occurred in the regional center, the direct economic losses of the earthquake with and without spatial correlation, fixed spatial distribution and random spatial distribution of regional building structures are calculated upon on the basis of different loss ratios. The results show that the loss ratio has an important influence on the accuracy of the assessment of the direct economic loss of regional earthquakes. Considering the spatial correlation, the Monte Carlo simulation statistics of the direct economic loss of regional portfolio building structures show a lognormal distribution, and the annual exceedance probability of the loss obtained by using Monte Carlo random simulation of the distribution of building structures is very close to the annual exceedance probability of fixed buildings on the whole. The annual exceedance probability of loss considering the spatial correlation of the ground motion influence field will be significantly greater than that of loss without considering the spatial correlation at the middle and high direct economic losses.
- regional portfolio buildings /
- probability loss estimation /
- direct economic loss /
- spatial correlation /
- geo-statistics

HTML全文

建筑物倒塌、人员伤亡和经济损失是评价历次大地震破坏的主要指标。历次地震灾害表明：建筑物倒塌造成95%以上的人员伤亡，建筑物倒塌或破坏是造成地震直接经济损失的主要因素^{[1 − 3]}。例如，1976年唐山Ms7.8级地震造成所有砖石结构建筑和绝大部分框架结构建筑物损坏，导致24.2万人死亡，直接经济损失100亿元以上。2008年汶川Ms8.0级地震造成7.9万人死亡，受灾总人口达4625.6万人，直接经济损失8451.4亿元。2010年青海玉树Ms7.1级地震造成的总经济损失为26 611.32万元，其中直接经济损失为18 114.52万元，占总损失70%以上^{[4 − 6]}。

地震经济损失评估作为地震风险分析的重要构成部分，是相关部门制定防震减灾政策的技术依据和理论基础。因此，如何精准地评估地震经济损失具有重要的理论意义和工程价值。在地震造成的损失中，建筑结构主体破坏所造成的损失最直观且量级最大。目前，地震灾害损失评估的方法主要有确定性方法和概率性方法。确定性震害评估是在假定某地区发生某种等级的地震情景下，对现时的建筑结构、生命线工程等进行直接的经济损失和人员伤亡评估；如果考虑当时的社会经济状况，还可预测出相应的间接损失。这种方法是以现在的建筑状况为分析依据，把未来可能遭遇的最大地震假设在现时发生。由于不考虑时间因素的影响，此方法更适用于实际地震发生后的地震损失评估。概率性方法假定地震的发生是一个随机事件，以设定概率的地震烈度为基础评价一个区域的地震损失，这种方法认为地震损失是评估区的地震危险性、工程结构的地震易损性和社会经济发展水平的函数，因而可以用来评价区域的地震损失风险水平，震害预测的结果可以作为选择和优化防震减灾决策的依据^[7]。

随着地震灾害和风险评估由单一结构向空间分布的建筑群落和基础设施的转变，PARK等^[8]、SOKOLOV和WENZEL^{[9 − 10]}证明了考虑空间相关性的地震动随机场在地震风险评估中的重要性。一次地震事件的激励是空间相关的，这种局部的空间相关可能会导致在一次地震事件中许多结构同时损坏的可能性增加。然而，只有当不同地点地震动强度之间的相关性已知时，才能实现对地震所造成破坏的准确量化。在该研究趋势的推动下，近年来，国内外学者分别对峰值地面加速度(PGA)、峰值地面速度(PGV)、谱加速度(S_a)^{[11 − 20]}、累积绝对速度(CAV)^[21]等地震动强度参数(Intensity Measures, IM)的事件内空间相关性(Intra-Event Spatial Correlation)进行了评估。地震动预测方程(Ground Motion Prediction Equations, GMPE)是概率地震危险性分析以及风险评估的重要工具，目前空间相关性的研究均从给定的GMPE中分离出相关残差进行空间地统计学(Geo-statistics)分析。利用地震动强度参数的空间相关性并结合GMPE模型模拟区域地震动强度参数的影响场，为区域地震损失评估提供了基础。

由于现实区域中建筑结构的种类、数量以及分布复杂，对其进行承灾体建模(Exposure Modeling)将会耗费大量的时间。本文提出一种考虑区域地震动强度空间相关性和群体建筑结构空间分布不确定性的概率损失评估框架，该框架采用地统计学方法表征地震动强度参数的空间相关性，采用“双层蒙特卡洛方法”分别模拟区域地震动的空间相关影响场和群体建筑结构的随机空间分布，可以实现高效、快速的群体建筑结构空间分布建模以及区域群体建筑结构直接经济损失评估。以某区域受到7.2级地震情景为例，对比分析考虑空间相关性与不考虑空间相关性以及群体建筑结构固定分布与随机分布情况下直接经济损失估计的差异。

1 考虑地震动空间相关性和建筑结构空间分布不确定性的区域群体建筑概率损失评估框架与流程

在我国，对于区域地震动影响场的构建，一般采用当地区域的设防烈度(GB 18306−2015中国地震动参数区划图)进行评估。通常情况下，设防烈度在指定区域范围内的峰值加速度PGA或其他地震动强度参数为一定值，没有考虑地震动强度参数在不同的空间位置间存在一定程度的空间相关性(短距离空间内，地震动强度参数的空间相关性较强)。对一个区域来讲，一个固定的地震动强度参数取值无法合理地表征地震动强度参数在空间中的变化趋势，因此，传统的方法存在低估或高估群体建筑结构地震直接经济损失的缺陷，因此构建具有空间相关性的区域地震动强度参数的随机影响场对建筑结构的损失评估更加准确，结果也更加接近现实。

通常发生地震的区域中建筑结构种类繁多、数量巨大，且分布没有规律性，如果对区域所有的建筑结构进行空间分布建模，将会耗费大量的时间与精力，使工作量徒增，因此很难采用真实的建筑结构空间分布进行精确区域建模，无法满足地震发生后的损失预测与紧急决策的需求。如图1所示，本文提出一种考虑地震动空间相关性和建筑结构空间分布不确定性的区域群体建筑直接经济损失概率评估框架，该框架包括四个模块：1)区域地震动强度参数的空间影响场构建；2)区域群体建筑结构易损性清单构建；3)区域群体建筑结构破坏状态确定；4)区域群体建筑地震直接经济损失评估。以下分别对4个模块进行简要介绍。

图 1 考虑地震动空间相关性与区域群体建筑结构空间分布不确定性的概率损失评估框架

Figure 1. Framework of probability loss estimation for regional portfolio buildings considering spatial correlation of ground motions and location uncertainties of building structures

下载: 全尺寸图片幻灯片

模块1：基于区域地震危险性分析结果^{[22 − 24]}，对区域进行网格划分，一般采用1 km×1 km或2 km×2 km的方型网格，这是因为在地震记录仪布置丰富的区域，其间隔距离一般在2 km以内。按照地统计学空间相关性的计算要求，所采用的距离步长Δh一般情况下取3 km，故可以认为在划分的网格区域范围内，地震动强度参数的空间相关性ρ = 1，即方型网格区域内不同建筑结构所受到的地震动强度参数为同一值。每次蒙特卡洛模拟将产生不同地震动强度的空间相关性随机影响场样本。

模块2：鉴于区域内建筑结构类型、分布以及设计标准的复杂性，对区域建筑结构进行分类统计，确定区域建筑结构的易损性清单。对于区域建筑结构损失的计算需要对群体建筑结构的空间分布精细建模，本文提出的评估框架仅需要提供各类建筑结构在此区域的总数量即可，对于每种不同的建筑结构在区域网格内进行空间均匀随机分布的蒙特卡洛模拟，将各种建筑结构空间分布的随机样本进行叠加，即可得到一种区域建筑结构的空间分布样本。

模块3：基于上述两个模块确定了每一个区域网格的地震动强度参数的取值，以及区域网格内所有建筑结构的类型与数量，此模块依据给定的每种建筑结构四种不同破坏状态的易损性曲线，确定区域中每一个建筑结构四种破坏状态的发生概率。

模块4：参考每种建筑结构的重置成本与四种不同破坏状态的损失比，通过计算该区域群体建筑结构地震直接经济损失值。

本评估框架采用“双层蒙特卡洛模拟”(即地震动空间影响场的模拟和区域群体建筑结构空间分布的模拟)评估区域群体建筑的地震直接经济损失，以考虑地震动强度参数影响场的不确定性以及区域群体建筑结构空间分布的不确定性对区域建筑结构损失评估的影响。概率损失评估的具体流程如图2所示，当对于不同区域进行地震损失评估时，该评估框架仅需对区域建筑结构类型及相应数量进行重新定义，从而使得评估过程简单、快速、高效地适用于各个地区的地震损失评估。具体评估流程如下：

图 2 考虑地震动空间相关性与区域群体建筑结构空间分布不确定性的概率损失评估流程图

Figure 2. Tree of probability loss estimation for regional portfolio buildings considering spatial correlation of ground motions and location uncertainties of building structures

下载: 全尺寸图片幻灯片

第一步：区域地震情景的构建，对区域进行网格划分，然后根据地统计学空间相关性随机理论，生成具有空间相关性的随机地震动影响场。每次循环将产生不同的地震动影响场，充分考虑了地震动影响场的随机性。

第二步：对区域内的建筑类型、数量、建筑规范标准等进行分类，统计各类建筑结构的数量，以及各类建筑结构四种不同破坏状态的易损性数据库清单，然后采用蒙特卡洛方法将每类建筑结构随机分布在区域空间中，最后叠加各类建筑结构的空间分布，获得一次区域建筑结构的空间样本。

第三步：根据构建的地震动影响场与建筑结构的空间分布，确定每个建筑结构在区域划分网格中发生不同破坏状态的概率，依据各类建筑结构的置换成本、损失比计算得到区域的群体建筑结构的直接经济损失。

第四步：循环上述过程10 000次，统计计算结果，进行数据分析。

2 考虑空间相关性的地震动影响场构建

2.1 地震动强度参数的空间相关性分析

地震发生时，相邻的台站所采集到的地震动观测数据通常具有明显的相关性，造成两个不同场点地震动IM具有相关性的主要原因有：1)由同一地震事件产生的地震动具有相同的断层破裂模型(震级、断层几何、震源中心、应力降、破裂速度与方向等)；2)一次地震事件的地震波通过类似的路径由震源传播到两个距离接近的场点，即具有相似的介质模型——地壳速度结构模型；3)如果断层破裂的尺寸相对于站点到震源的距离较大或较小时，则相邻的场点将远离或靠近断层破裂的凹凸体。

地震动预测方程GMPE是用来表征地震动IM随震级、距离、场地等因素变化规律的预测模型。由于缺乏明确的物理解释，预测模型中没有包含的变量会造成观察值和预测模型之间存在差异，即偶然不确定性(Aleatory Uncertainty)，通常在模型中添加额外的解释变量来表征偶然不确定性。GMPE中一般将偶然不确定性分为地震事件间(Inter-event)的不确定性(称为“事件间残差”)和同一次地震事件内(Intra-event)不同场点间的不确定性(称为“事件内残差”)，以表征地震动强度参数的随机性。事件间残差通常是由预测模型对不同的地震事件进行回归产生的偶然不确定性，反映不同地震事件发生时断层的破裂机制对地震动IM造成的差异。事件内残差反映给定事件不同地点的地震动在一定程度上发生变化的事实，主要取决于传播路径和场地条件。

在地震动预测方程GMPE中，通常假设IM服从对数正态分布。针对地震事件k，特定场点台站i的地震动强度参数的预测方程为：

$\ln ({Y_{ik}}) = \ln {\overline Y_{ik}}(M,R,\theta ) + {\eta _k} + {\varepsilon _{ik}}$

(1)

式中：Y_ik为地震事件k发生时，台站i处的地震动强度参数，通常为S_a、PGA、PGV、I_a等强度参数指标； ${\overline Y_{ik}}(M,R,\theta )$ 为在给定的震级(M)、震源距(R)以及其他参数(θ)下地震动预测方程估计该地震动强度参数的中位值；η_k为事件间残差，一般假设服从均值为0、标准差为σ_η的独立正态分布，对于给定地震事件的所有台站的地震动记录；η_k为一常数，代表不同地震事件IM均值的系统偏差；ε_ik为事件内残差，一般假设服从均值为0、标准差为σ_ε的独立正态分布。总残差的标准差可以表示为 $\sigma_{\mathrm{T}}=\left(\sigma_\eta{ }^2+\sigma_{{\mathrm{\varepsilon}}}{ }^2\right)^{1 / 2}$ 。

由于假设IM服从对数正态分布，因此对数化地震动强度参数服从正态分布：

$\ln ({Y_{ik}}) \sim {\text{N}}(\ln {\overline Y_{ik}}(M,R,\theta ),{\sigma _{\mathrm{T}}})$

(2)

对于第k次地震事件中两个距离为Δ_ij的随机台站i和台站j之间总残差，η_k(T₁)+ε_ik(T₁)与η_k(T₂)+ε_jk(T₂)的相关性可以表示为^[15]：

$\begin{split} &{\rho _{\mathrm{T}}}(\varDelta ,{T_1},{T_2}) = \\ &\frac{{{\rho _\eta }({T_1},{T_2}){\sigma _\eta }({T_1}){\sigma _\eta }({T_2}) + {\rho _{\text{ε}} }(\varDelta ,{T_1},{T_2}){\sigma _{\text{ε}} }({T_1}){\sigma _{\text{ε}} }({T_2})}}{{{\sigma _{\mathrm{T}}}({T_1}){\sigma _{\mathrm{T}}}({T_2})}} \end{split}$

(3)

式中：ρ_η(T₁, T₂)为事件间残差η_k(T₁)与η_k(T₂)之间的相关性；ρ_ε(Δ, T₁, T₂)代表着事件内残差ε_ik(T₁)与ε_jk(T₂)的相关性。其中T₁与T₂表示的是不同的谱加速度周期，当T₁=T₂时，ρ_η(T_n, T_n)=1，式(3)可以简化为：

$\begin{split} {\rho _{\mathrm{T}}}(\varDelta ,{T_n}) =& \frac{{{\sigma _\eta }{{({T_n})}^2} + {\rho _{\text{ε}} }(\varDelta ,{T_n}){\sigma _{\text{ε}} }{{({T_n})}^2}}}{{{\sigma _{\mathrm{T}}}{{({T_n})}^2}}}= \\ & {\rho _\eta }({T_n}) + {\rho _{\text{ε}} }(\varDelta ,{T_n}) \cdot \frac{{{\sigma _{\text{ε}} }{{({T_n})}^2}}}{{{\sigma _{\mathrm{T}}}{{({T_n})}^2}}} \end{split}$

(4)

式中，ρ_η(T_n)为地震动的事件间相关性，是指同一地点在不同地震期间地震动不确定性的相似性，由不确定性分量之间的关系决定：

${\rho _\eta }({T_n}) = \frac{{{\sigma _\eta }{{({T_n})}^2}}}{{{\sigma _\eta }{{({T_n})}^2} + {\sigma _{\text{ε}} }{{({T_n})}^2}}} = \frac{{{\sigma _\eta }{{({T_n})}^2}}}{{{\sigma _{\mathrm{T}}}{{({T_n})}^2}}}$

(5)

由于地震波传播过程的相似性，两个靠近的站点可能在一次地震事件中表现出地震动IM的相关性，即事件内空间相关性ρ_ε(Δ, T_n)，主要取决于站点间隔距离Δ，通常采用地统计学(Geo-statistics)方法进行计算。

2.2 基于地统计学的空间相关性计算

半变异函数是地统计学中研究空间变异性的工具函数，用来表征随机变量的空间变异结构，或空间连续性。当随机变量的均值不随位置x变化，其协方差Cov[V(x),V(y)]取决于样本点x和y之间的距离h时，满足随机变量二阶平稳假设^[25]，即：

$\left\{ {\begin{aligned} &{E\left[ {{V_i}({{{\boldsymbol{x}}}})} \right] = {m_i}},&& {\forall i \in 1,2, \ldots ,n} \\ &{E\left[ {({V_i}({{{\boldsymbol{x}}}}) - {m_i})({V_j}({{{\boldsymbol{y}}}}) - {m_j})} \right] = {C_{ij}}({{{\boldsymbol{h}}}})},&& {\forall i,j \in 1,2, \ldots ,n} \end{aligned}} \right.$

(6)

先前的研究^{[14, 18]}已经证明，地震动事件内残差的空间相关性ρ_ε并不取决于空间间距的方向，同时一般假设事件内残差空间分布的各向同性，因此可以考虑将空间间距表示为 $h = \left\| {\boldsymbol{h}} \right\|$ ，即半变异函数可以表示为：

$\begin{split} & \gamma (h) = \frac{1}{2}{{\mathrm{Var}}}\left[ {V(u + h) - V(u)} \right] =\\ &\quad\frac{1}{2}{\left[ {{\boldsymbol{E}}(V(u + h) - V(u))} \right]^2} - \frac{1}{2}{\boldsymbol{E}}[ {{{(V(u + h) - V(u))}^2}} ] \end{split}$

(7)

由于地震动的事件内残差满足二阶平稳假设，因此：

$\gamma (h) = \frac{1}{2}{\boldsymbol{E}} [ {{{(V(u + h) - V(u))}^2}} ]$

(8)

经验半变异函数 $\tilde \gamma (h)$ 可以表示为：

$\tilde \gamma (h) = \frac{1}{{2N(h)}}\sum\limits_{i = 1}^{N(h)} {{{[V({u_i} + h) - V({u_i})]}^2}}$

(9)

式中：h为空间两点间距离N(h)表示样本间所有距离为h的台站对的个数；V(u_i+h)与V(u_i)分别代表距离为h时两台站的事件内残差值。

与半变异函数类似的协方差C(h)可以表示为：

$\begin{split} C(h) = &{{\mathrm{Cov}}} (V(u),V(u + h)) = {E} [ (V(u) - {E} \left[ {V(u)} \right])\cdot\\ &(V(u + h) - {E} \left[ {V(u + h)} \right]) ] \\[-1pt] \end{split}$

(10)

同时联立式(9)与式(10)可得：

$\gamma (h) = C(0) - C(h)$

(11)

同时事件内残差的空间相关性函数ρ_ε(h)可以表示为：

${\rho _{\text{ε}} }(h) = \frac{{C(h)}}{{C(0)}}$

(12)

结合式(11)与式(12)可得：

$\gamma (h) = C(0)\left[ {1 - {\rho _{\text{ε}} }(h)} \right] = {{\mathrm{Var}}} (V)\left[ {1 - {\rho _{\text{ε}} }(h)} \right]$

(13)

从而将半变异函数γ(h)与相关性函数ρ_ε(h)进行结合，可以通过对半变异函数的估计来获得随机变量的空间相关性分布。一般将地震事件内残差的进行标准化处理，则式(13)可简化为：

${\rho _{\text{ε}} }(h) = 1 - \gamma (h)$

(14)

可以使用几个基本函数形式来近似经验半变异函数数据γ(h)，如指数函数模型、高斯函数模型、球面半变异函数模型。由于指数模型具有明显的简单性以及短距离区间内对空间相关性实现良好表征的优势，BAKER等^{[14, 20]}、ESPOSITO等^{[18 − 19]}、DU和WANG^[21]采用该模型对经验半变异函数数据γ(h)进行拟合：

$\gamma (h) = a[1 - \exp ( - 3h/b)]$

(15)

式中：a为基台(sill)；b为变程(range)。在指数模型中，一般取95%基台对应的变程b值作为空间相关距。为了保证短距离空间相关性的可靠性，通常采用加权最小二乘法进行拟合。

2.3 地震动空间影响场的构建

在给定地震事件k与场点i的情况下，地震动IM(这里为 $\ln ({Y_{ik}})$ )服从式(1)所示正态分布的随机变量，中位值 $\ln ({\overline Y_{ik}})$ 可以根据GMPE获得，同时也可以得到事件间残差标准差σ_η和事件内残差标准差σ_ε，因此需要生成服从正态分布的事件间残差η_k和事件内残差ε_ik。

由于IM不仅在给定位置呈边缘正态分布，对于i=1,2…, m，m个场点的IMs服从多元正态分布的假设。为了生成空间相关的地震动IMs总残差的m维随机场，首先生成具有总残差空间相关的标准正态随机变量，组成多元正态向量X = [X₁, X₂, …, X_m] ~N_m(0, Σ)，其中Σ为相关系数矩阵：

${\boldsymbol{\varSigma}} { = \left( {\begin{array}{*{20}{c}} 1&{{\rho _{12}}}& \cdots &{{\rho _{1m}}} \\ {{\rho _{21}}}&1& \vdots &{{\rho _{2m}}} \\ \vdots & \vdots & \vdots & \vdots \\ {{\rho _{m1}}}&{{\rho _{m2}}}& \cdots &1 \end{array}} \right)}$

(16)

式中，ρ_ij为根据式(4)计算不同场点之间的空间相关系数。为了构建空间相关的k个站点地震事件内残差随机场，采用k维高斯Copula模型的相关矩阵Σ生成随机向量X=[X₁, X₂,…, X_k](其中X_j为j台站的事件间残差与事件内残差的总和)。具体步骤为：

1)生成独立的0均值、方差为σ_ij²的正态向量U=[U₁, U₂,…, U_k]，即：U_k~N(0, σ_ij²)；

2)对相关矩阵Σ进行Cholesky分解，即Σ=BB^T；

3)采用下式获得随机向量X：

${\boldsymbol{X}} = {\boldsymbol{BU}}$

(17)

图3所示为不考虑空间相关性及考虑空间相关距为25 km的PGA的总残差空间分布图。可以看出，考虑空间相关性的残差分布变化更加均匀，这也符合真实场地强度参数的空间分布特征，不考虑空间相关性(ρ_T=0)的强度参数分布具有强随机性。

图 3 地震动强度参数的残差分布

Figure 3. Residual distribution of IMs

下载: 全尺寸图片幻灯片

3 建筑结构空间分布不确定性的模拟

区域建筑是一个复杂的系统，该系统包含建筑结构的分布位置特征、类型特征、功能特征等^[26]。对于区域群体建筑结构的地震直接经济损失评估而言，建筑结构的分布与类型尤为重要，建筑结构清单的构建可采用HAZUS提供的建筑结构分类标准，而对于区域中建筑结构的分布，并没有明确的方法。通常区域群体建筑结构总的直接经济损失可采用叠加每个建筑结构在指定位置处的直接经济损失来计算。考虑到地震动强度参数的空间相关性，以及区域中建筑结构空间分布的复杂性，需要分别单独计算特定位置处建筑结构的地震直接经济损失。因受复杂的社会和自然因素的影响，区域种建筑结构群体分布的准确建模尤为复杂，因此本文采用蒙特卡洛随机空间均匀分布的方法对区域群体建筑结构的分布进行模拟，其具体的步骤：

1) 确定区域范围内的建筑结构的类型；

2) 确定每种建筑结构的数量；

3) 基于区域划分的网格，分别对每种建筑结构进行蒙特卡洛随机空间均匀分布模拟；

4) 将每种建筑结构的空间分布进行叠加，获得建筑结构随机空间分布的一个样本。

建筑结构空间分布不确定性的模拟流程如图4所示。

图 4 蒙特卡洛随机模拟群体建筑结构分布流程图

Figure 4. Flow chart of structure distribution of group buildings by Monte Carlo random simulation

下载: 全尺寸图片幻灯片

4 区域群体建筑地震直接经济损失的概率评估

地震作用下，区域群体建筑的经济损失分为直接经济损失和间接经济损失两大类，其中评估区域地震灾害直接经济损失的方法有现场调查法、遥感识别法、易损性分类清单法等^[29]。所谓易损性分类清单法，是在一定的地震烈度作用下，对于指定的研究地域，分别预测各种结构的损失，然后相加得到总损失的评估。该方法具有相对成熟、易操作、准确度较高、建筑物调查资料可提前准备等优点，适合对城市区域进行震害预测和快速评估，是目前国际上应用最为广泛的地震损失评估方法之一^{[26 − 30]}。

易损性分类清单法包含两部分内容：1)地震强度与结构破坏程度的关系；2)结构破坏程度和经济损失的关系。通常用地震易损性函数描述地震强度与结构破坏程度的关系，即结构在不同强度地震作用下，发生某一指定破坏状态的条件超越概率：

${F_{\text{R}}}(x) = P[D {\geqslant} C|{\mathrm{IM}} = x]$

(18)

式中：F_R(x)为地震易损性函数；D≥C为结构达到或超过某种极限状态，D为地震作用下结构的需求，C为结构的抗震能力；IM为地震动强度指标Sa(T₁)/g。

地震工程中通常将结构的破坏状态(Damage State)分为五个破坏等级：基本完好(DS₀)、轻微破坏(DS₁)、中等破坏(DS₂)、严重破坏(DS₃)、完全破坏即倒塌(DS₄)。一般采用对数正态分布对处于或超过破坏状态DS_i的条件概率进行建模：

$P[{\mathrm{DS}} > {\mathrm{D{S}}_i}|{\mathrm{IM}} = x] = {F_{{{\text{R}}_i}}}(x) = \varPhi \left[ {\frac{{\ln (x/{m_{{x_i}}})}}{{{\beta _i}}}} \right]$

(19)

式中： ${m_{{x_i}}}$ 为在给定地震动的前提条件下发生破坏状态下地震动强度参数IM的中位值； ${\beta _i}$ 为相应破坏状态下的对数标准差；Φ[·]为标准正态累积分布函数。

本文以于晓辉^[31]建立的典型8层RC框架结构的地震易损性函数(如图5所示)为例，确定IM在不同取值下发生不同损伤状态的概率。该过程是地震损失评估的基础。

图 5 不同损伤状态下的易损性函数

Figure 5. Fragility function under different damage states

下载: 全尺寸图片幻灯片

根据式(19)可以获得结构在不同极限状态下的失效概率，进一步可按下式计算结构处于不同破坏状态的概率：

${F_{{\text{D}}{{\text{S}}_i}}}({\mathrm{IM}}) = P[{\text{D}}{{\text{S}}_i}|{\mathrm{IM}}] = \left\{ \begin{aligned} &{1 - {F_{{\mathrm{R}_1}}}({\mathrm{IM}})}, & & i = 0 \\ & {{F_{{\mathrm{R}_i}}}({\mathrm{IM}}) - {F_{{\mathrm{R}_{i + 1}}}}({\mathrm{IM}})} , & & i = 1,2,3\\ & {{F_{{\mathrm{R}_4}}}({\mathrm{IM}})} , & & i = 4 \end{aligned}\right.$

(20)

损失比(Loss Ratio, LR)是建筑结构处于某一损伤状态时的经济损失与其重置成本(Replacement Cost, RC)之比，用来描述结构破坏程度和经济损失的关系。如果知道某种建筑结构的重置成本以及破坏状态DS_i下的损失比(LR_i)：

${{{\mathrm{LR}}} _i} = \frac{{{{{{\mathrm{RC}}} }_{{\text{repair,}}i}}}}{{{{{{\mathrm{RC}}} }_{{\text{replacement}}}}}},\quad i = 0,1,\cdots ,4$

(21)

式中： ${{{\mathrm{RC}}} _{{\text{repair,}}i}}$ 为破坏状态DS_i下结构的修复成本； ${{{\mathrm{RC}}} _{{\text{replacement}}}}$ 为建筑结构的重置成本RC。

则可以按下式可以得到单体建筑结构的期望直接损失(Expected Direct Loss, EDL)：

${{\mathrm{EDL}}} = {{\mathrm{RC}}} \cdot \sum\limits_{{\text{D}}{{\text{S}}_i}} {{{{{\mathrm{LR}}} }_i} \times {F_{{\text{D}}{{\text{S}}_i}}}({\mathrm{IM}})}$

(22)

对于区域中不同的建筑类型以及不同数量的建筑结构来讲，区域群体建筑结构的期望直接损失EDL_PB为：

${{{\mathrm{EDL}}} _{{\text{PB}}}} = \sum\limits_{m = 1}^m {\sum\limits_{n = 1}^n {{{{{\mathrm{EDL}}} }_{m,n}}} }$

(23)

式中：m为区域中不同类型建筑结构的种类；n为区域中每种建筑结构类型的总数量；EDL_{m, n}为单体建筑结构的期望直接损失。

损失比的取值是地震损失评估中一个十分重要的环节，尤其是大震时，破坏范围大，建筑面积大，损失比取值较小的变化就会引起总损失有较大的变化。为了较为直接、客观地表征损失比的取值对损失评估的影响，通常采用期望损失比(Expected Loss Ratio, ELR)来表征，定义为在给定地震强度参数下，不同破坏状态发生概率与相应破坏状态下损失比的乘积之和：

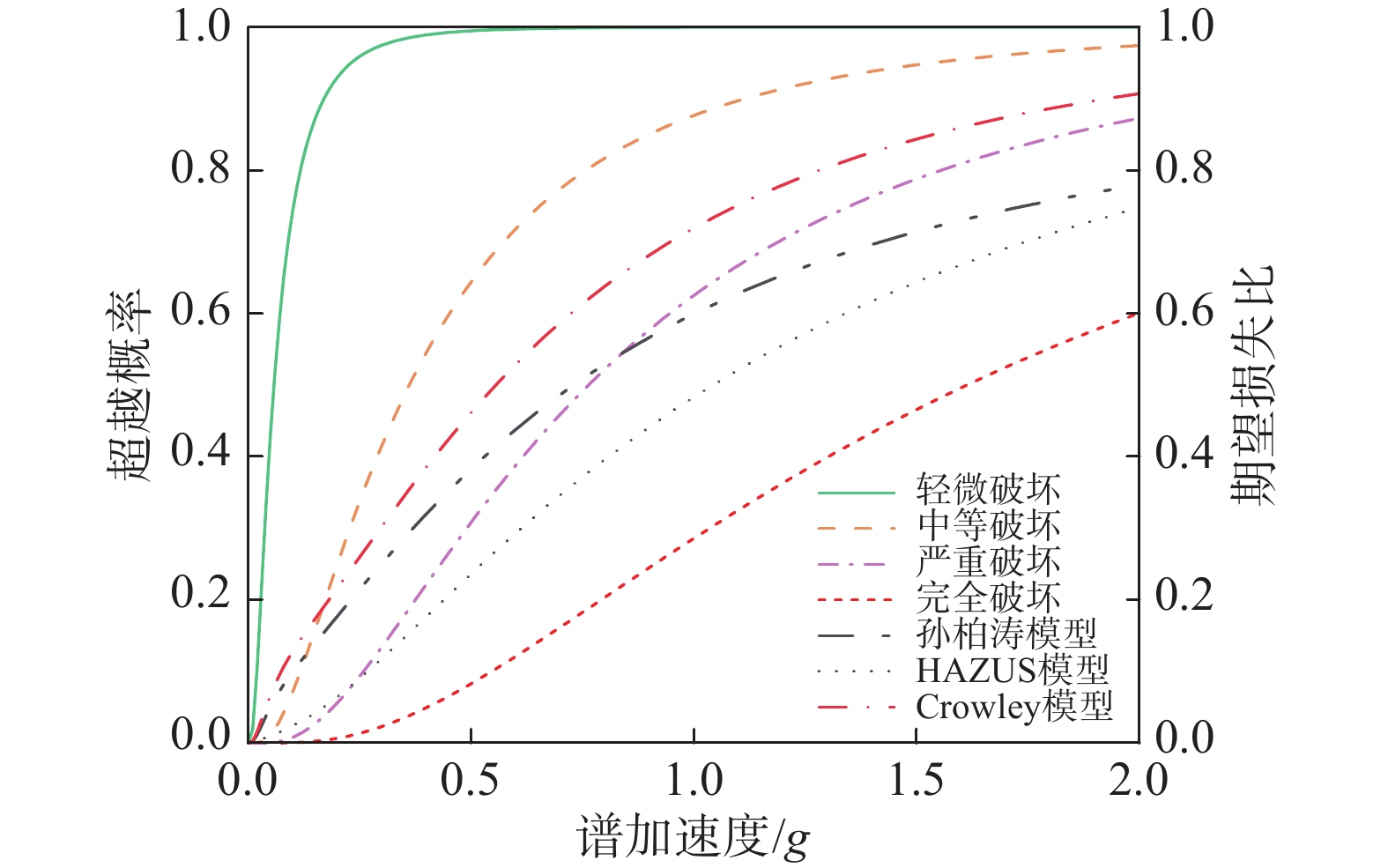
${{\mathrm{ELR}}} ({\mathrm{IM}}) = \sum\limits_{{\text{D}}{{\text{S}}_{\text{i}}}} {{{{{\mathrm{LR}}} }_i} \times {F_{{\text{D}}{{\text{S}}_i}}}({\mathrm{IM}})}$

(24)

孙柏涛等^[32]、陈洪富^[33]依据我国地震损失的真实状况，采用问卷调查方式，咨询了数十位熟悉该领域的国内专家及装饰装修公司人员，然后进行加权统计，给出了建筑破坏损失比的合理取值，但其只针对钢筋混凝土结构和砌体结构，并建议一般可取该取值范围的中值进行经济损失分析，结合地震现场工作规范^[34]要求规定：基本完好为0.03，轻微破坏为0.11，中等破坏为0.31，严重破坏为0.73，完全破坏为0.91。美国的损失评估软件HAZUS^[35]综合各类建筑并进行统计，建议损失比分别为：轻微破坏0.02、中等破坏0.1、严重破坏0.5、完全破坏1.0。而CROWLEY等^[36]则建议：轻微破坏0.15，中等破坏0.3，严重破坏和完全破坏1.0。本文以上述8层RC框架结构为例，依据孙柏涛等^[32]、HAZUS^[35]与CROWLEY等^[36]提供的损失比，进一步验证损失比对损失评估的影响，如图6所示，左侧纵坐标表示结构不同破坏状态的易损性曲线，右侧纵坐标表示不同损失比模型下该结构在不同地震动强度下的期望损失比曲线，可以发现：HAZUS^[35]提供的损失比整体小于CROWLEY等^[36]与孙柏涛等^[32]提供的损失比，导致在每一强度参数下的期望损失比存在较大的差异，因此合理的损失比取值对于精确评估地震的直接经济损失具有重要的意义。

图 6 不同损失比下的期望损失比

Figure 6. ERCR of different repair cost ratio

下载: 全尺寸图片幻灯片

5 案例分析

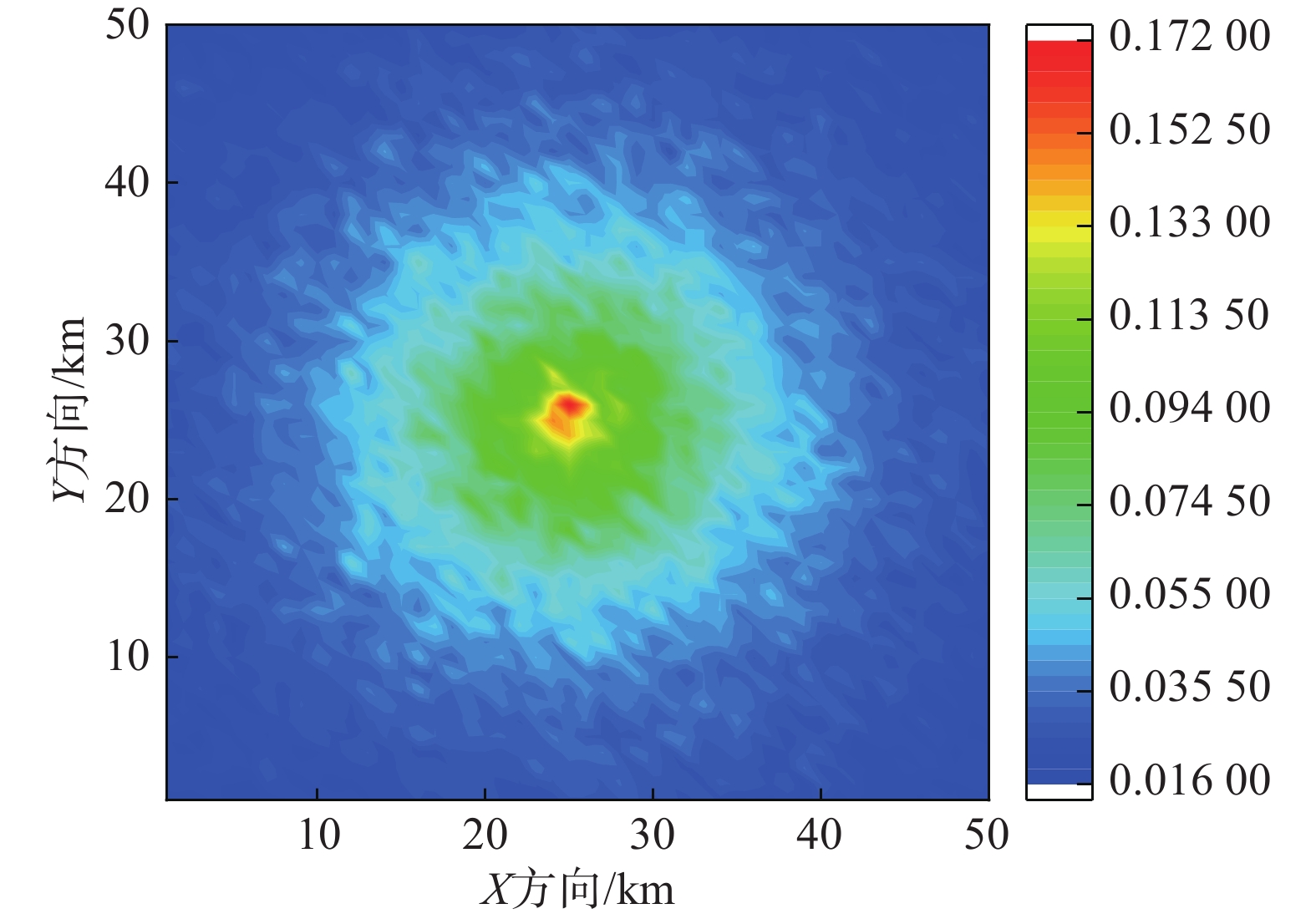
为展示本文提出的概率地震损失评估框架，假设一个50 km×50 km的区域，震源位于区域中心处，并将该区域划分为1 km×1 km的网格，假定该区域的断层为正断层，区域的平均场地条件为基岩，假设剪切波速服从均值为V_s30=600 m/s、标准差为50 m/s的正态分布。此区域仅存在一个潜在震源断层，该断层仅产生震级为M_w7.2级的地震，年平均发生率为0.01，震源深度为15 km的设定情景地震事件，假定震源中心位于区域中心处，如图7所示。通过地震动预测方程CY14^[37]来获取每一区域网格的预测地震动IM的中位值和对数标准差，图8所示为根据上述条件得到的PGA预测中位值。

图 7 情景地震震源及区域分布

Figure 7. Source and regional distribution of scenario earthquakes

下载: 全尺寸图片幻灯片

图 8 PGA的预测中位值分布图

Figure 8. Distribution of PGA predicted median

下载: 全尺寸图片幻灯片

孙柏涛等^{[32 − 33]}通过对汶川地震现场调查、收集造价资料和问卷调查的形式对我国城市典型建筑结构的类型进行了统计，结果显示，砌体结构、混凝土框架结构(带剪力墙)、钢筋混凝土结构以及钢支撑框架结构等是我国建筑结构的主要类型。本文基于多年来国内典型不同建筑结构的易损性的研究成果^{[38 − 45]}，对典型结构构建有限元模型进行非线性动力分析，得出了基于PGA的建筑结构不同破坏状态的地震易损性曲线。假定该区域共存在10 000个建筑结构，假设该区域存在5种主要的建筑结构形式：无筋砌体低层结构(URML 1层)、混凝土低层结构(CL 3层)、钢支撑低层框架结构(SL 3层)、钢筋混凝土低层结构(SRCL 5层)、钢筋混凝土中层结构(SRCM 10层)，假设建筑结构的数量比例为1∶1∶1∶1∶1。表1所示为5种建筑结构不同破坏状态易损性函数的中位值以及对数标准差β，以及重置成本。

表 1 建筑结构不同破坏状态易损性函数的中位值、对数标准差和重置成本

Table 1. Median, standard deviation and replacement cost of fragility function of structure under different damage states

建筑结构的类型	不同破坏状态的中位值PGA/g				重置成本/万元(RMB)
建筑结构的类型	轻微破坏	中等破坏	严重破坏	完全破坏	重置成本/万元(RMB)
URML	0.20	0.30	0.40	0.50	50
CL	0.28	0.45	0.55	0.65	200
SL	0.25	0.45	0.62	0.72	200
SRCL	0.35	0.55	0.65	0.75	350
SRCM	0.28	0.52	0.62	0.72	750
β	0.50	0.45	0.40	0.40	−

下载: 导出CSV

| 显示表格

假设此区域的PGA空间相关距b=25 km，根据第1节、第2节的内容，可以在此建设区域生成具有空间相关性PGA的地震动影响场分布图(ShakeMap)样本，如图9(a)所示，其中不考虑空间相关性PGA的ShakeMap样本如图9(b)所示。可以发现，具有空间相关性的PGA影响场强度分布更加均匀，更加符合地震动强度参数真实空间分布的衰减特征。如图10所示，本文预先假定了建筑结构真实固定分布的模型，并分别计算固定建筑结构分布情况与随机空间分布情况下的地震直接经济损失的差异，同时以HAZUS提供的损失比与孙柏涛提供的损失比为例，对比分析了不同损失比下地震直接经济损失的差异。

图 9 PGA分布图

Figure 9. PGA distribution

下载: 全尺寸图片幻灯片

图 10 假定建筑结构的真实固定空间分布模型

Figure 10. Fixed spatial distribution model of assumed buildings

下载: 全尺寸图片幻灯片

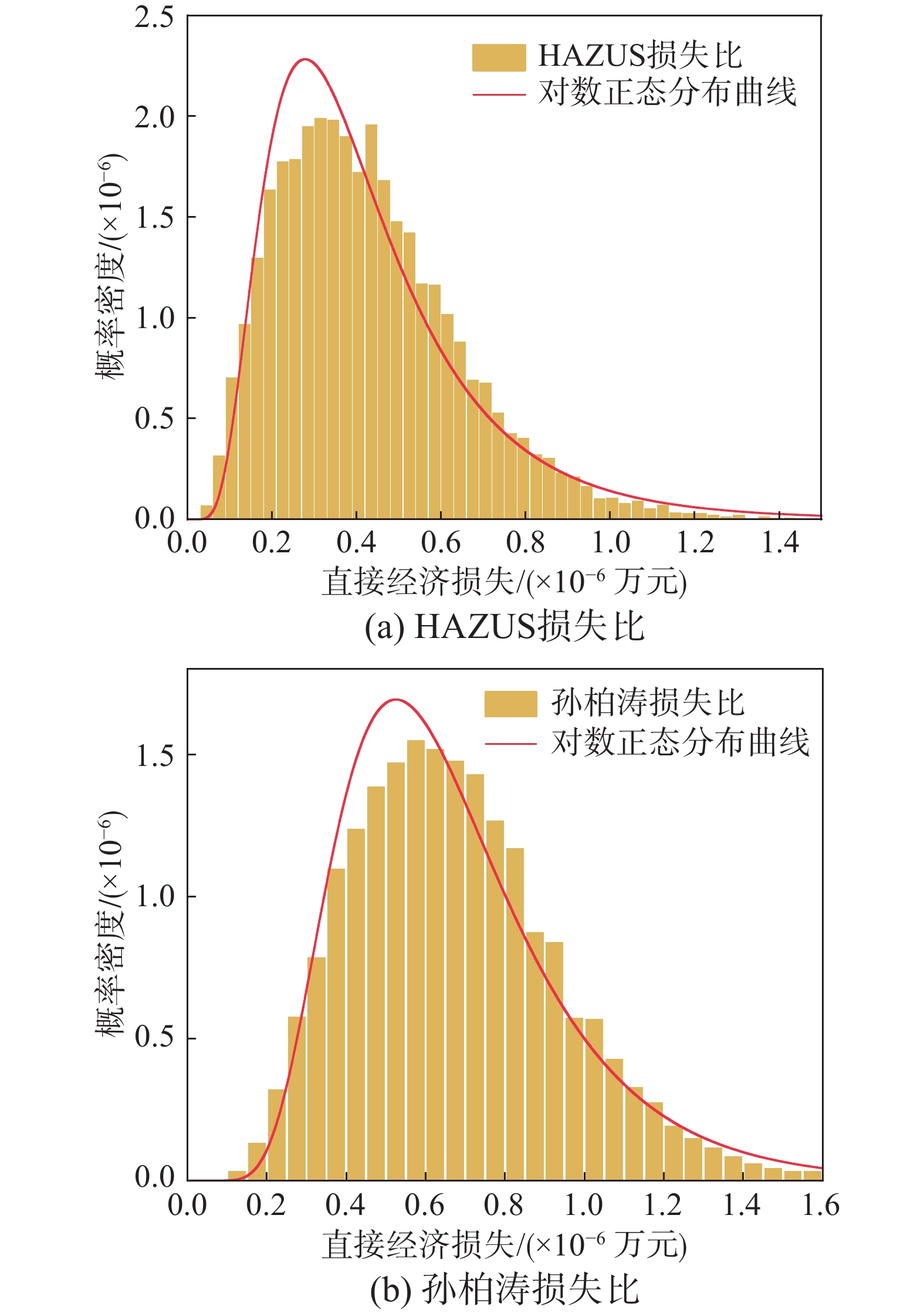
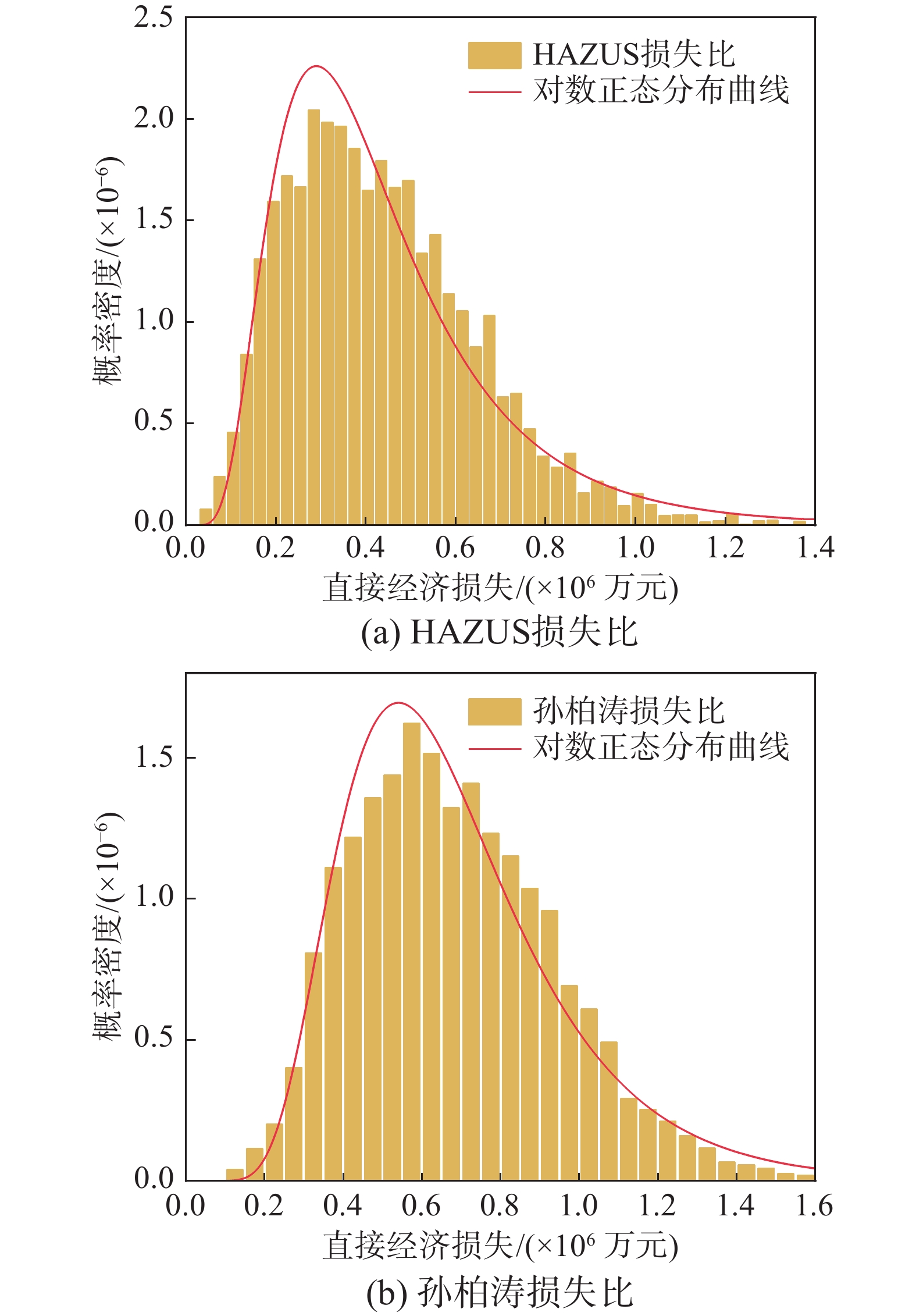
基于本文提出的区域群体建筑概率损失评估框架，计算了考虑空间相关性的情况下，建筑结构真实固定空间分布模型分别以HAZUS损失比与孙柏涛损失比为基础，模拟10 000次该区域群体建筑结构的地震直接经济损失的统计结果，如图11(a)、图11(b)所示。图12(a)、图12(b)为考虑空间相关性的情况下随机蒙特卡洛建筑结构随机空间分布模型即：“双层蒙特卡洛模拟”下直接经济损失的统计结果。图13、图14分别为不考虑地震动强度空间相关性的条件下，建筑结构真实固定空间分布与随机空间分布在不同损失比下的直接经济损失的计算结果。对比图11~图14可以发现，在考虑空间相关性影响场的条件下，无论固定分布还是随机分布的损失评估结果均服从对数正态分布，而不考虑空间相关性影响场的条件下，损失结果服从正态分布。不同损失比下的计算结果很不同，可以看出依据孙柏涛损失比计算的直接经济损失估计值相对于HAZUS损失比计算结果偏大，验证了期望损失比(ELR)对精确评估区域损失评估准确的重要性。

图 11 考虑空间相关性影响场下结构固定分布的直接经济损失模拟结果

Figure 11. Simulation results of direct economic loss of fixed buildings distribution with spatial correlation influence field

下载: 全尺寸图片幻灯片

图 12 考虑空间相关性影响场下结构随机分布的直接经济损失模拟结果

Figure 12. Simulation results of direct economic loss of stochastic buildings distribution with spatial correlation influence field

下载: 全尺寸图片幻灯片

图 13 不考虑空间相关性影响场下结构固定分布的直接经济损失模拟结果

Figure 13. Simulation results of direct economic loss of fixed buildings distribution without spatial correlation influence field

下载: 全尺寸图片幻灯片

图 14 不考虑空间相关性影响场下结构随机分布的直接经济损失模拟结果

Figure 14. Simulation results of direct economic loss of stochastic buildings distribution without spatial correlation influence field

下载: 全尺寸图片幻灯片

表2所示为不同情形下区域群体建筑的地震直接经济损失的概率统计模型及参数，可以看出在考虑地震动空间相关性随机场的条件下建筑结构随机分布的平均值均大于固定建筑分布，同时标准差更小，说明本文提出的区域群体地震概率损失评估框架可以较好地消除建筑结构空间分布随机性对损失结果的影响。当不考虑空间相关性时，建筑结构随机分布时的均值和标准差均大于固定建筑结构分布的损失结果，从而说明空间地震动影响场的随机性与建筑结构分布的随机性将会提高损失结果。

表 2 不同情形下直接经济损失的概率统计模型及参数

Table 2. Probability statistical models and parameters of direct economic losses under different cases

情形	固定建筑结构分布				随机建筑结构分布
	HAZUS损失比		孙柏涛损失比		HAZUS损失比		孙柏涛损失比
	μ	σ	μ	σ	μ	σ	μ	σ
考虑空间相关性	12.8301	0.5424	13.3409	0.4123	12.8578	0.5290	13.3619	0.4017
考虑空间相关性	对数正态分布		对数正态分布		对数正态分布		对数正态分布
不考虑空间相关性	426 520	16 458	671 770	19 068	433 740	17 071	682 190	19 643
不考虑空间相关性	正态分布		正态分布		正态分布		正态分布

下载: 导出CSV

| 显示表格

表3对比了两种不同群体建筑结构分布下的蒙特卡洛10 000次损失结果的均值、标准差、中位值以及90%和99%的分位值。图15(a)所示为8种不同情况下10 000次蒙特卡洛模拟的直接经济损失的均值，可以发现建筑结构随机空间分布的地震直接经济损失均值相对于固定分布平均偏大约1.28%，中位值整体偏大约2.17%，本文基于10 000次群体建筑结构随机空间分布蒙特卡洛模拟的结果与建筑结构真实固定分布计算得到的区域地震直接经济损失值十分接近。虽然考虑建筑结构的随机空间分布会在一定程度上轻微提高地震直接经济损失的评估结果，但此评估体系相对复杂的区域建筑结构真实固定分布建模来讲，计算、建模效率有了很大的提升。孙柏涛损失比模型具有更高的期望损失比，从而导致其在计算区域直接经济损失时明显大于依据HAZUS损失比计算的结果，偏大约57.47%。因此，损失比的估计对于区域直接经济损失的估计起到重要的作用，合理的损失比估计是精确评估区域损失重要基础。

表 3 蒙特卡洛模拟的地震直接经济损失的统计结果及参数

Table 3. Statistical results and parameters of direct economic losses of earthquakes simulated by Monte Carlo

参数	固定建筑结构分布				随机建筑结构分布
	HAZUS损失比		孙柏涛损失比		HAZUS损失比		孙柏涛损失比
	考虑空间相关性	不考虑空间相关性	考虑空间相关性	不考虑空间相关性	考虑空间相关性	不考虑空间相关性	考虑空间相关性	不考虑空间相关性
均值	426 640	426 520	673 700	671 770	435 890	433 740	685 230	682 190
标准差	212 980	16 459	261 530	19 069	212 160	17 071	258 790	19 644
变异系数	0.4992	0.0386	0.3882	0.0284	0.4867	0.0394	0.3777	0.0288
中位值	395 685	426 390	647 085	671 760	435 890	433 740	685 230	682 190
90%分位值	713 235	447 660	1 025 655	696 600	718 620	455 760	1 030 470	707 340
99%分位值	1 056 780	465 405	1 395 405	715 830	1 038 375	474 345	1 377 855	730 680

下载: 导出CSV

| 显示表格

图 15 10 000次蒙特卡洛模拟结果的参数对比

Figure 15. Parameter comparison of 10 000 Monte Carlo simulation results

下载: 全尺寸图片幻灯片

在考虑区域地震动影响场空间相关性的情况下，区域地震直接经济损失均值相比未考虑空间相关性损失的均值偏大1%左右，但是随机空间分布下地震损失结果的标准差却小于固定分布损失标准差的1.95%，无论建筑结构随机分布还是固定分布，在考虑地震动空间相关性时，计算得到的标准差明显大于未考虑空间相关性的损失结果，如图15(b)所示，进而导致90%分位值和99%分位值相比未考虑空间相关性的损失评估结果更大，从而说明考虑空间相关性将在在一定程度上提高了严重的直接经济损失概率。

图16分别以HAZUS损失比与孙柏涛损失比为基础，并依据10 000次蒙特卡洛模拟的结果，根据式(25)计算得到不同模型下的区域群体建筑直接经济损失的年超越概率(Expected Annual Loss, EAL)：

图 16 区域群体建筑直接经济损失的年超越概率

Figure 16. Annual exceedance probability of direct economic loss of regional group buildings

下载: 全尺寸图片幻灯片

${\lambda _{{{\mathrm{EAL}}} }} = {\upsilon _{{\text{earthquake}}}} \cdot P(x > {{\mathrm{loss}}} |x)$

(25)

式中：λ_EAL为直接经济损失的年超越概率；υ_earthquake为地震的发生概率；P(x>loss|x)为超过指定损失loss的超越概率，x为模拟得到的直接经济损失值。

考虑空间相关性与不考虑空间相关性得到的年超越概率具有较大的区别，在低直接经济损失时，不考虑空间相关性的年超越损失概率明显大于考虑空间相关性的计算结果，而考虑空间相关性将会造成更高年超越经济损失概率，可以发现建筑结构固定分布与建筑结构随机分布无论在考虑空间相关性或不考虑空间相关性时的年超越概率差别不大，说明本文采用的蒙特卡洛随机空间均匀模拟区域群体建筑结构分布具有一定的可靠性。

为进一步明确比较建筑结构固定分布与建筑结构随机分布分别在考虑与不考虑空间相关性时的年超越概率的区别，分别采用上述模拟得到的10 000次蒙特卡洛模拟的结果，以建筑结构随机分布并考虑空间相关性影响场为基准，分别计算不同模型下的直接经济损失年超越概率的比值，如图17所示，可以发现，损失比对其比值影响很小，建筑结构固定分布在考虑空间相关性的情况下在低、中经济损失处与随机建筑结构分布考虑空间相关性的情况基本一致，比率范围在0.9~1.1，而在高经济损失时，考虑固定建筑结构分布的经济损失与随机建筑结构分布的经济损失比率出现较大偏差，最小比率达到0.7，整体上采用蒙特卡洛随机空间均匀模拟区域群体建筑结构分布的直接经济损失年超越概率与真实固定建筑结构分布的年超越损失概率基本保持一致，而不考虑地震动强度参数的空间相关性下的区域群体建筑结构的直接经济损失在中高处存在明显的区别。

图 17 区域群体建筑的直接经济损失之间的比较

Figure 17. Comparison between direct economic losses of regional group buildings

下载: 全尺寸图片幻灯片

6 结论

本文提出了一种考虑空间相关性与群体建筑结构空间分布不确定性的区域群体建筑直接经济损失概率评估框架，该框架可以通过双层蒙特卡洛模拟，分别考虑地震动影响场的强度分布的随机性与区域群体建筑结构分布的不确定性。以一个典型的案例对该评估框架进行了初步应用，得到以下结论：

(1)考虑地震动影响场空间相关性的条件下，区域地震直接经济损失10 000次随机模拟结果呈对数正态分布，而不考虑空间相关性的条件下呈正态分布。

(2)不同的损失比模型对区域地震直接经济损失评估的结果产生很大的影响，期望损失比的大小直接影响损失评估的精度。

(3)建筑结构真实固定分布的直接经济损失均值与随机分布的结果十分接近，说明本文提出的损失评估框架可以较好地解决区域群体建筑空间分布复杂性的难题。建筑结构随机分布的直接经济损失年超越概率与建筑结构真实固定分布的直接经济损失年超越概率在整体变化趋势上保持了一致，验证了本文提出的损失评估框架的可靠性和准确性。

(4)考虑地震动空间相关性会得到更高的区域直接经济损失年超越概率，而不考虑空间相关性的将会导致更高的低经济损失年超越概率。

图 1 考虑地震动空间相关性与区域群体建筑结构空间分布不确定性的概率损失评估框架

Figure 1. Framework of probability loss estimation for regional portfolio buildings considering spatial correlation of ground motions and location uncertainties of building structures

下载: 全尺寸图片幻灯片

图 2 考虑地震动空间相关性与区域群体建筑结构空间分布不确定性的概率损失评估流程图

Figure 2. Tree of probability loss estimation for regional portfolio buildings considering spatial correlation of ground motions and location uncertainties of building structures

下载: 全尺寸图片幻灯片

图 3 地震动强度参数的残差分布

Figure 3. Residual distribution of IMs

下载: 全尺寸图片幻灯片

图 4 蒙特卡洛随机模拟群体建筑结构分布流程图

Figure 4. Flow chart of structure distribution of group buildings by Monte Carlo random simulation

下载: 全尺寸图片幻灯片

图 5 不同损伤状态下的易损性函数

Figure 5. Fragility function under different damage states

下载: 全尺寸图片幻灯片

图 6 不同损失比下的期望损失比

Figure 6. ERCR of different repair cost ratio

下载: 全尺寸图片幻灯片

图 7 情景地震震源及区域分布

Figure 7. Source and regional distribution of scenario earthquakes

下载: 全尺寸图片幻灯片

图 8 PGA的预测中位值分布图

Figure 8. Distribution of PGA predicted median

下载: 全尺寸图片幻灯片

图 9 PGA分布图

Figure 9. PGA distribution

下载: 全尺寸图片幻灯片

图 10 假定建筑结构的真实固定空间分布模型

Figure 10. Fixed spatial distribution model of assumed buildings

下载: 全尺寸图片幻灯片

图 11 考虑空间相关性影响场下结构固定分布的直接经济损失模拟结果

Figure 11. Simulation results of direct economic loss of fixed buildings distribution with spatial correlation influence field

下载: 全尺寸图片幻灯片

图 12 考虑空间相关性影响场下结构随机分布的直接经济损失模拟结果

Figure 12. Simulation results of direct economic loss of stochastic buildings distribution with spatial correlation influence field

下载: 全尺寸图片幻灯片

图 13 不考虑空间相关性影响场下结构固定分布的直接经济损失模拟结果

Figure 13. Simulation results of direct economic loss of fixed buildings distribution without spatial correlation influence field

下载: 全尺寸图片幻灯片

图 14 不考虑空间相关性影响场下结构随机分布的直接经济损失模拟结果

Figure 14. Simulation results of direct economic loss of stochastic buildings distribution without spatial correlation influence field

下载: 全尺寸图片幻灯片

图 15 10 000次蒙特卡洛模拟结果的参数对比

Figure 15. Parameter comparison of 10 000 Monte Carlo simulation results

下载: 全尺寸图片幻灯片

图 16 区域群体建筑直接经济损失的年超越概率

Figure 16. Annual exceedance probability of direct economic loss of regional group buildings

下载: 全尺寸图片幻灯片

图 17 区域群体建筑的直接经济损失之间的比较

Figure 17. Comparison between direct economic losses of regional group buildings

下载: 全尺寸图片幻灯片

表 1 建筑结构不同破坏状态易损性函数的中位值、对数标准差和重置成本

Table 1 Median, standard deviation and replacement cost of fragility function of structure under different damage states

建筑结构的类型	不同破坏状态的中位值PGA/g				重置成本/万元(RMB)
建筑结构的类型	轻微破坏	中等破坏	严重破坏	完全破坏	重置成本/万元(RMB)
URML	0.20	0.30	0.40	0.50	50
CL	0.28	0.45	0.55	0.65	200
SL	0.25	0.45	0.62	0.72	200
SRCL	0.35	0.55	0.65	0.75	350
SRCM	0.28	0.52	0.62	0.72	750
β	0.50	0.45	0.40	0.40	−

下载: 导出CSV

表 2 不同情形下直接经济损失的概率统计模型及参数

Table 2 Probability statistical models and parameters of direct economic losses under different cases

情形	固定建筑结构分布				随机建筑结构分布
	HAZUS损失比		孙柏涛损失比		HAZUS损失比		孙柏涛损失比
	μ	σ	μ	σ	μ	σ	μ	σ
考虑空间相关性	12.8301	0.5424	13.3409	0.4123	12.8578	0.5290	13.3619	0.4017
考虑空间相关性	对数正态分布		对数正态分布		对数正态分布		对数正态分布
不考虑空间相关性	426 520	16 458	671 770	19 068	433 740	17 071	682 190	19 643
不考虑空间相关性	正态分布		正态分布		正态分布		正态分布

下载: 导出CSV

表 3 蒙特卡洛模拟的地震直接经济损失的统计结果及参数

Table 3 Statistical results and parameters of direct economic losses of earthquakes simulated by Monte Carlo

参数	固定建筑结构分布				随机建筑结构分布
	HAZUS损失比		孙柏涛损失比		HAZUS损失比		孙柏涛损失比
	考虑空间相关性	不考虑空间相关性	考虑空间相关性	不考虑空间相关性	考虑空间相关性	不考虑空间相关性	考虑空间相关性	不考虑空间相关性
均值	426 640	426 520	673 700	671 770	435 890	433 740	685 230	682 190
标准差	212 980	16 459	261 530	19 069	212 160	17 071	258 790	19 644
变异系数	0.4992	0.0386	0.3882	0.0284	0.4867	0.0394	0.3777	0.0288
中位值	395 685	426 390	647 085	671 760	435 890	433 740	685 230	682 190
90%分位值	713 235	447 660	1 025 655	696 600	718 620	455 760	1 030 470	707 340
99%分位值	1 056 780	465 405	1 395 405	715 830	1 038 375	474 345	1 377 855	730 680

下载: 导出CSV

参考文献(45)

[1]	李文俊. 我国典型房屋建筑地震易损性模型研究[D]. 哈尔滨: 中国地震局工程力学研究所, 2021. LI Wenjun. Research on seismic vulnerability models of typical buildings in China [D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 2021. (in Chinese)
[2]	郑山锁, 尚志刚, 贺金川, 等. 地震灾害经济损失评估方法及应用[J]. 灾害学, 2020, 35(1): 94 − 101. doi: 10.3969/j.issn.1000-811X.2020.01.018 ZHENG Shansuo, SHANG Zhigang, HE Jinchuan, et al. Method and application of economic loss assessment for earthquake disasters [J]. Journal of Catastrophology, 2020, 35(1): 94 − 101. (in Chinese) doi: 10.3969/j.issn.1000-811X.2020.01.018
[3]	吴琼. 地震直接经济损失快速评估方法研究[D]. 西安: 西安建筑科技大学, 2015. WU Qiong. Study on the rapid assessment method of earthquake-caused direct economic loss [D]. Xi’an: Xi’an University of Architecture and Technology, 2015. (in Chinese)
[4]	林向洋, 文鑫涛, 李华玥, 等. 2019年中国大陆地震灾害损失述评[J]. 震灾防御技术, 2020, 15(3): 473 − 483. doi: 10.11899/zzfy20200301 LIN Xiangyang, WEN Xintao, LI Huayue, et al. Review of earthquake damage losses in mainland of China in 2019 [J]. Technology for Earthquake Disaster Prevention, 2020, 15(3): 473 − 483. (in Chinese) doi: 10.11899/zzfy20200301
[5]	谭婷. 中国高地震风险区基于性能的建筑直接经济损失估计[D]. 重庆: 重庆大学, 2011. TAN Ting. Performance-based direct economic loss estimation for buildings in high seismic hazard areas of China [D]. Chongqing: Chongqing University, 2011. (in Chinese)
[6]	黄孝昆. 中国大陆地震经济损失评估方法研究[D]. 哈尔滨: 中国地震局工程力学研究所, 2015. HUANG Xiaokun. Study on loss assessment methodology of earthquake disaster in mainland China [D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 2015. (in Chinese)
[7]	毕可为. 群体建筑的易损性分析和地震损失快速评估[D]. 大连: 大连理工大学, 2009. BI Kewei. Vulnerability analysis of group buildings and earthquake loss fast estimation [D]. Dalian: Dalian University of Technology, 2009. (in Chinese)
[8]	PARK J, BAZZURRO P, BAKER J W. Modeling spatial correlation of ground motion intensity measures for regional seismic hazard and portfolio loss estimation [J]. Applications of Statistics and Probability in Civil Engineering, 2007, 2: 1 − 8.
[9]	SOKOLOV V, WENZEL F. Influence of spatial correlation of strong ground motion on uncertainty in earthquake loss estimation [J]. Earthquake Engineering & Structural Dynamics, 2011, 40(9): 993 − 1009.
[10]	SOKOLOV V, WENZEL F. Influence of ground-motion correlation on probabilistic assessments of seismic hazard and loss: Sensitivity analysis [J]. Bulletin of Earthquake Engineering, 2011, 9(5): 1339 − 1360. doi: 10.1007/s10518-011-9264-4
[11]	BOORE D M, GIBBS J F, JOYNER W B, et al. Estimated ground motion from the 1994 Northridge, California, earthquake at the site of the interstate 10 and La Cienega boulevard bridge collapse, west los Angeles, California [J]. Bulletin of the Seismological Society of America, 2003, 93(6): 2737 − 2751. doi: 10.1785/0120020197
[12]	WANG M, TAKADA T. Macrospatial correlation model of seismic ground motions [J]. Earthquake Spectra, 2005, 21(4): 1137 − 1156. doi: 10.1193/1.2083887
[13]	GODA K, HONG H P. Spatial correlation of peak ground motions and response spectra [J]. Bulletin of the Seismological Society of America, 2008, 98(1): 354 − 365. doi: 10.1785/0120070078
[14]	JAYARAM N, BAKER J W. Correlation model for spatially distributed ground-motion intensities [J]. Earthquake Engineering & Structural Dynamics, 2009, 38(15): 1687 − 1708.
[15]	GODA K, ATKINSON G M. Intraevent spatial correlation of ground-motion parameters using SK-net data [J]. Bulletin of the Seismological Society of America, 2010, 100(6): 3055 − 3067. doi: 10.1785/0120100031
[16]	SOKOLOV V, WENZEL F, JEAN W Y, et al. Uncertainty and spatial correlation of earthquake ground motion in Taiwan [J]. Terrestrial Atmospheric and Oceanic Sciences, 2010, 21(6): 905 − 921. doi: 10.3319/TAO.2010.05.03.01(T)
[17]	SOKOLOV V, WENZEL F, WEN K L, et al. On the influence of site conditions and earthquake magnitude on ground-motion within-earthquake correlation: Analysis of PGA data from TSMIP (Taiwan) network [J]. Bulletin of Earthquake Engineering, 2012, 10(5): 1401 − 1429. doi: 10.1007/s10518-012-9368-5
[18]	ESPOSITO S, IERVOLINO I. PGA and PGV spatial correlation models based on European Multievent datasets [J]. Bulletin of the Seismological Society of America, 2011, 101(5): 2532 − 2541. doi: 10.1785/0120110117
[19]	ESPOSITO S, IERVOLINO I. Spatial correlation of spectral acceleration in European data [J]. Bulletin of the Seismological Society of America, 2012, 102(6): 2781 − 2788. doi: 10.1785/0120120068
[20]	CHEN Y L, BAKER J W. Spatial correlations in CyberShake physics‐based ground‐motion simulations [J]. Bulletin of the Seismological Society of America, 2019, 109(6): 2447 − 2458. doi: 10.1785/0120190065
[21]	DU W Q, WANG G. Intra-event spatial correlations for cumulative absolute velocity, arias intensity, and spectral accelerations based on regional site conditions [J]. Bulletin of the Seismological Society of America, 2013, 103(2A): 1117 − 1129. doi: 10.1785/0120120185
[22]	熊维, 王迪晋, 余鹏飞, 等. 历史强震对2017九寨沟M_W6.5地震的应力影响及区域地震危险性[J]. 地球物理学进展, 2019, 34(1): 19 − 26. doi: 10.6038/pg2019BB0562 XIONG Wei, WANG Dijin, YU Pengfei, et al. Coulomb stress impact on 2017 Jiuzhaigou M_W 6.5 earthquake induced by historical earthquakes and Regional Seismic Hazard [J]. Progress in Geophysics, 2019, 34(1): 19 − 26. (in Chinese) doi: 10.6038/pg2019BB0562
[23]	GERSTENBERGER M C, MARZOCCHI W, ALLEN T, et al. Probabilistic seismic hazard analysis at Regional and National Scales: State of the art and future challenges [J]. Reviews of Geophysics, 2020, 58(2): e2019RG000653. doi: 10.1029/2019RG000653
[24]	FÜLÖP L, MÄNTYNIEMI P, MALM M, et al. Probabilistic seismic hazard analysis in low-seismicity regions: An investigation of sensitivity with a focus on Finland [J]. Natural Hazards, 2023, 116(1): 111 − 132. doi: 10.1007/s11069-022-05666-4
[25]	GOOVAERTS P. Geostatistics for natural resources evaluation [M]. New York: Oxford University Press, 1997.
[26]	丛阳, 余丁浩, 李钢, 等. 城市综合体多层级功能损失及抗震韧性评估方法[J]. 建筑结构学报, 2023, 44(7): 1 − 14. CONG Yang, YU Dinghao, LI Gang, et al. Multi-level function loss and seismic resilience assessment method of urban complex [J]. Journal of Building Structures, 2023, 44(7): 1 − 14. (in Chinese)
[27]	陈尧, 林均岐, 刘金龙, 等. 地震直接经济损失快速评估方法研究[J]. 世界地震工程, 2017, 33(1): 188 − 193. CHEN Yao, LIN Junqi, LIU Jinlong, et al. Study on rapid assessment method of earthquake direct economic loss [J]. World Earthquake Engineering, 2017, 33(1): 188 − 193. (in Chinese)
[28]	董尧, 徐铭阳, 吕大刚. 高层RC框架-剪力墙结构地震风险与抗震韧性评估[J]. 建筑结构学报, 2022, 43(增刊1): 31 − 42. DONG Yao, XU Mingyang, LYU Dagang. Seismic risk and resilience assessment for high-rise RC frame-shear wall structures [J]. Journal of Building Structures, 2022, 43(S1): 31 − 42. (in Chinese)
[29]	许镇, 陆新征, 韩博, 等. 城市区域建筑震害高真实度模拟[J]. 土木工程学报, 2014, 47(7): 46 − 52. XU Zhen, LU Xinzheng, HAN Bo, et al. Realistic simulation for seismic damages of buildings in an urban area [J]. China Civil Engineering Journal, 2014, 47(7): 46 − 52. (in Chinese)
[30]	叶良浩, 曲哲, 孙海林, 等. 采用不同减震结构体系的医疗建筑地震经济损失评估[J]. 建筑结构学报, 2020, 41(7): 15 − 26. YE Lianghao, QU Zhe, SUN Hailin, et al. Earthquake loss evaluation of medical facility seismically retrofitted by different seismic damage control methods [J]. Journal of Building Structures, 2020, 41(7): 15 − 26. (in Chinese)
[31]	于晓辉. 钢筋混凝土框架结构的概率地震易损性与风险分析[D]. 哈尔滨: 哈尔滨工业大学, 2012. YU Xiaohui. Probabilistic seimic fragility and risk analysis of reinforced concrete frame structures [D]. Harbin: Harbin Institute of Technology, 2012. (in Chinese)
[32]	孙柏涛, 陈洪富. 计及城市房屋建筑装修破坏的地震经济损失评估方法研究[J]. 地震工程与工程振动, 2009, 29(5): 164 − 169. SUN Baitao, CHEN Hongfu. Urban building loss assessment method considering the decoration damage due to earthquake [J]. Journal of Earthquake Engineering and Engineering Vibration, 2009, 29(5): 164 − 169. (in Chinese)
[33]	陈洪富. 城市房屋建筑装修震害损失评估方法研究[D]. 哈尔滨: 中国地震局工程力学研究所, 2008. CHEN Hongfu. Study on earthquake damage loss assessment of urban buildings’ decorations [D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 2008. (in Chinese)
[34]	GB/T 18208.4−2011, 地震现场工作第4部分: 灾害直接损失评估[S]. 北京: 中国标准出版社, 2012. GB/T 18208.4−2011, Post-earthquake field works—Part 4: Assessment of direct loss [S]. Beijing: Standards Press of China, 2012. (in Chinese)
[35]	Federal Emergency Management Agency. Multi-hazard loss estimation methodology. Earthquake model [R]. Washington, DC: HAZUS-MH MR1 Technical Manual, 2003.
[36]	CROWLEY H, BOMMER J J, PINHO R, et al. The impact of epistemic uncertainty on an earthquake loss model [J]. Earthquake Engineering & Structural Dynamics, 2005, 34(14): 1653 − 1685.
[37]	CHIOU B S J, YOUNGS R R. Update of the Chiou and Youngs NGA model for the average horizontal component of peak ground motion and response spectra [J]. Earthquake Spectra, 2014, 30(3): 1117 − 1153. doi: 10.1193/072813EQS219M
[38]	于晓辉, 吕大刚. HAZUS相容的钢筋混凝土框架结构地震易损性分析[J]. 工程力学, 2016, 33(3): 152 − 160. doi: 10.6052/j.issn.1000-4750.2014.08.0685 YU Xiaohui, LYU Dagang. HAZUS-compatible seismic fragility analysis for RC frame structures [J]. Engineering Mechanics, 2016, 33(3): 152 − 160. (in Chinese) doi: 10.6052/j.issn.1000-4750.2014.08.0685
[39]	于晓辉, 吕大刚, 范峰. 基于易损性指数的钢筋混凝土框架结构地震损伤评估[J]. 工程力学, 2017, 34(1): 69 − 75,100. doi: 10.6052/j.issn.1000-4750.2015.09.0731 YU Xiaohui, LYU Dagang, FAN Feng. Seismic damage assessment of RC frame structures based on vulnerabilty index [J]. Engineering Mechanics, 2017, 34(1): 69 − 75,100. (in Chinese) doi: 10.6052/j.issn.1000-4750.2015.09.0731
[40]	于晓辉, 李越然, 宋鹏彦, 等. 极限状态模糊性对地震易损性分析的影响研究: 以钢筋混凝土框架结构为例[J]. 工程力学, 2021, 38(9): 89 − 99,109. doi: 10.6052/j.issn.1000-4750.2020.08.0604 YU Xiaohui, LI Yueran, SONG Pengyan, et al. Effect of fussiness at limit states on seismic fragility analysis: Reinforced concrete frame cases [J]. Engineering Mechanics, 2021, 38(9): 89 − 99,109. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.08.0604
[41]	于晓辉, 李雁军, 吕大刚, 等. 基于易损性的RC框架填充墙结构概率地震安全评估[J]. 土木工程学报, 2014, 47(增刊2): 260 − 265. YU Xiaohui, LI Yanjun, LYU Dagang, et al. Fragility-based probabilistic seismic safety assessment of RC frame structures with infilled masonry walls [J]. China Civil Engineering Journal, 2014, 47(Suppl 2): 260 − 265. (in Chinese)
[42]	郑晓伟, 李宏男, 张营营, 等. 基于概率的高层建筑地震需求模型与风险评估[J]. 工程力学, 2022, 39(9): 31 − 39. doi: 10.6052/j.issn.1000-4750.2021.05.0329 ZHENG Xiaowei, LI Hongnan, ZHANG Yingying, et al. Probabilistic seismic demand models and risk assessment for high-rise buildings [J]. Engineering Mechanics, 2022, 39(9): 31 − 39. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.05.0329
[43]	蒋亦庞, 苏亮, 黄鑫. 考虑参数不确定性的无筋砌体结构地震易损性分析[J]. 工程力学, 2020, 37(1): 159 − 167. doi: 10.6052/j.issn.1000-4750.2019.01.0068 JIANG Yipang, SU Liang, HUANG Xin. Seismic fragility analysis of unreinforced masonry structures considering parameter uncertainties [J]. Engineering Mechanics, 2020, 37(1): 159 − 167. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.01.0068
[44]	石运东, 卫旺旺, 丁阳, 等. 三维隔震钢框架结构及内部非结构构件地震易损性研究[J]. 工程力学, 2024, 41(1): 149 − 159. doi: 10.6052/j.issn.1000-4750.2022.03.0227 SHI Yundong, WEI Wangwang, DING Yang, et al. Seismic fragility study of three-dimensional isolated steel frame structure and non-structural components [J]. Engineering Mechanics, 2024, 41(1): 149 − 159. (in Chinese) doi: 10.6052/j.issn.1000-4750.2022.03.0227
[45]	张永群, 蒋利学, 王卓琳. 基于性能的多层砌体结构地震易损性分析[J]. 建筑结构学报, 2021, 42(5): 64 − 71. ZHANG Yongqun, JIANG Lixue, WANG Zhuolin. Performance-based seismic vulnerability analysis of multi-story masonry structures [J]. Journal of Building Structures, 2021, 42(5): 64 − 71. (in Chinese)