钢-混凝土组合梁桥通过剪力连接件将普通混凝土(normal concrete，NC)和钢材结合，充分发挥混凝土抗压、钢材抗拉的优势，具有构件高度小、刚度大、适用性好等特点^{[1 − 2]}。在传统工字钢-NC组合板梁桥中，其钢梁布置大量加劲肋以增强稳定性，从而钢构件数量多且焊接疲劳效应显著。波形钢腹板由于其波折式的结构特征，相比于平钢腹板具有较高的稳定性，采用其替代传统工字钢的平钢腹板可显著减少钢构件数量，增加钢主梁的横向刚度而进一步增大主梁间距，降低钢材用量，更有利于提高制作工业化效率^{[3 − 4]}。然而，在长期处于复杂环境的运营过程中，桥面板易出现铺装损坏和疲劳开裂等长期困扰桥梁工程界的耐久性问题，严重危及桥梁安全使用性能，同时桥面板自重大、负弯矩区易开裂等问题制约组合梁跨径进一步发展^{[5 − 6]}。

超高性能混凝土(ultra high performance concrete, UHPC)的研发为高性能桥梁体系建设带来了根本性突破。UHPC材料由普通硅酸盐水泥、硅灰、钢纤维等多种材料组成，是一种高韧性，高抗压、拉强度和耐久性能良好，徐变、收缩小的新型水泥基复合材料^[7]。波形钢腹板-NC组合板梁桥构造简便、便于施工，而UHPC具有优异的力学和耐久性能，这两者的结合可以实现组合梁桥的高性能化，波形钢腹板的褶皱效应可充分发挥UHPC高强度特点，还有效避免传统装配施工钢-混组合板梁桥负弯矩区开裂及耐久性等难题，并且还可以减小桥面板厚度，从而达到提高桥梁跨径的目的。目前，国外近十余年来已建成多座UHPC桥梁，国内外学者已对UHPC结构体系从局部到整体开展系统研究工作，并取得了较好的研究进展。石雪飞等^[8]、戚家南等^[9]将UHPC材料应用于预制拼装桥面板接缝，研究不同设计参数对接缝受力性能的影响。朱劲松等^[10]、童乐为等^[11]研究了钢-UHPC组合梁抗剪连接件的抗拔、抗剪和疲劳性能，分析了栓钉设计参数对此新型界面连接力学性能的影响。樊健生等^[12]、刘君平^[13]、ZHANG等^[14]对钢-UHPC组合箱型桥和工字型组合梁桥开展抗弯性能试验，展示了钢-UHPC组合梁典型弯曲破坏形态。邵旭东等^{[15 − 16]}提出钢-UHPC轻型组合桥面体系，通过开展试验研究了其抗弯性能和开裂特征，并给出合理构造设计建议。张清华等^[17]、GHASEMI等^[18]引入UHPC华夫板替代NC桥面板，分析了华夫板设计参数对组合梁力学性能的影响规律。

综上可知，UHPC桥面板与NC桥面板相比，不仅耐久性和疲劳性能优异，厚度更薄，从而提升桥梁的跨越能力。但是，UHPC板同时带来的还有相较于NC板数十倍的建设成本，使其在实际应用过程中受到限制。朱经纬等^[19]开展了钢-UHPC-NC组合梁受弯性能试验，充分发挥UHPC材料优势的同时减少了UHPC用量，提高经济性。LIU等^[20]通过开展试验将钢-UHPC-NC组合梁与钢-NC、钢-UHPC组合梁作对比，分析了桥面板设计参数对抗弯性能的影响。然而，迄今少有文献研究波形钢腹板-UHPC-NC组合梁的抗弯性能。本文通过开展两组波形钢腹板工字钢组合梁试验，研究波形钢腹板-UHPC-NC组合梁与波形钢腹板-NC组合梁受力性能的差别，并通过数值模拟给出合理构造参数设计建议。

1   试验概况

1.1   试验梁设计与制作

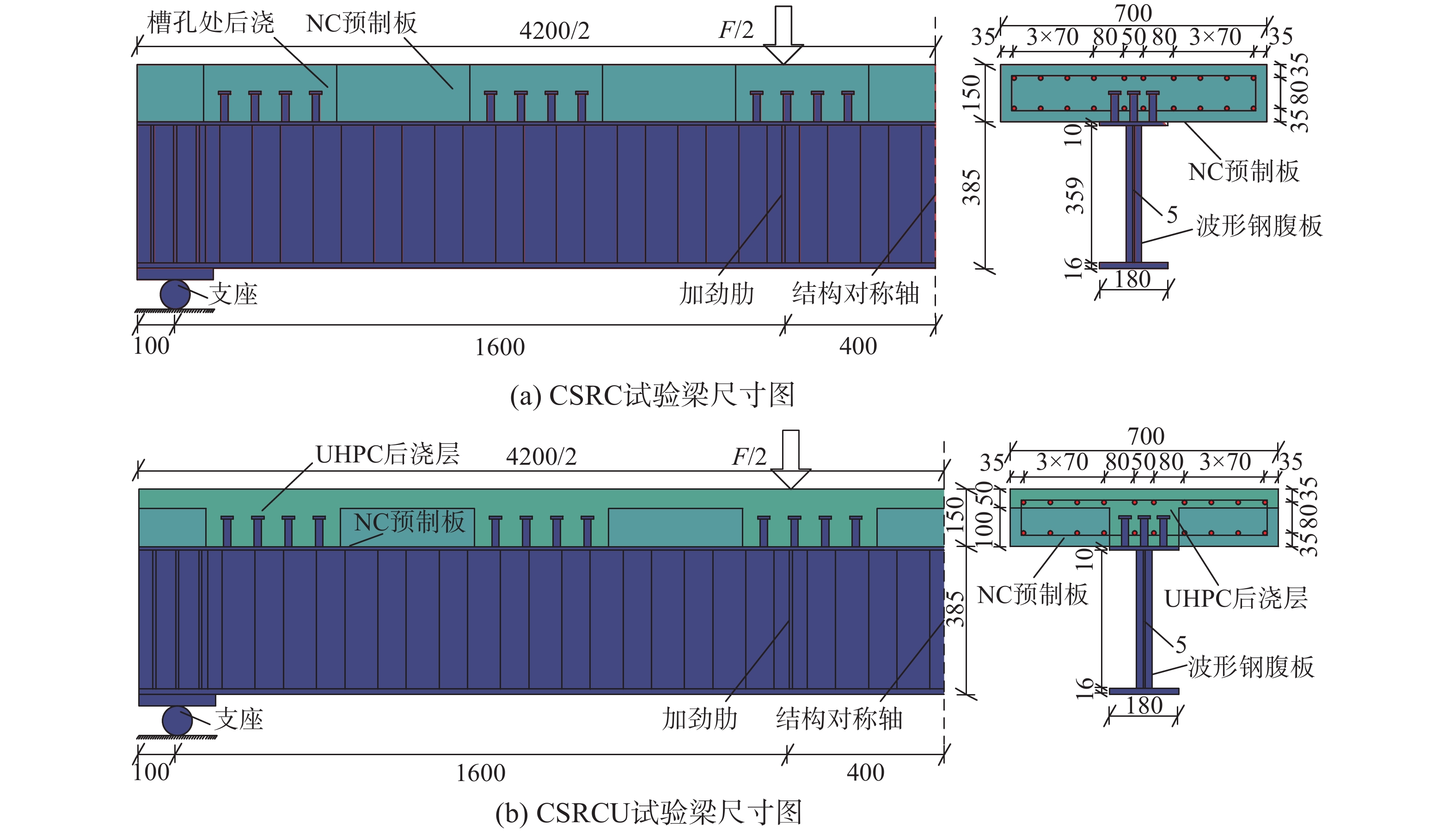
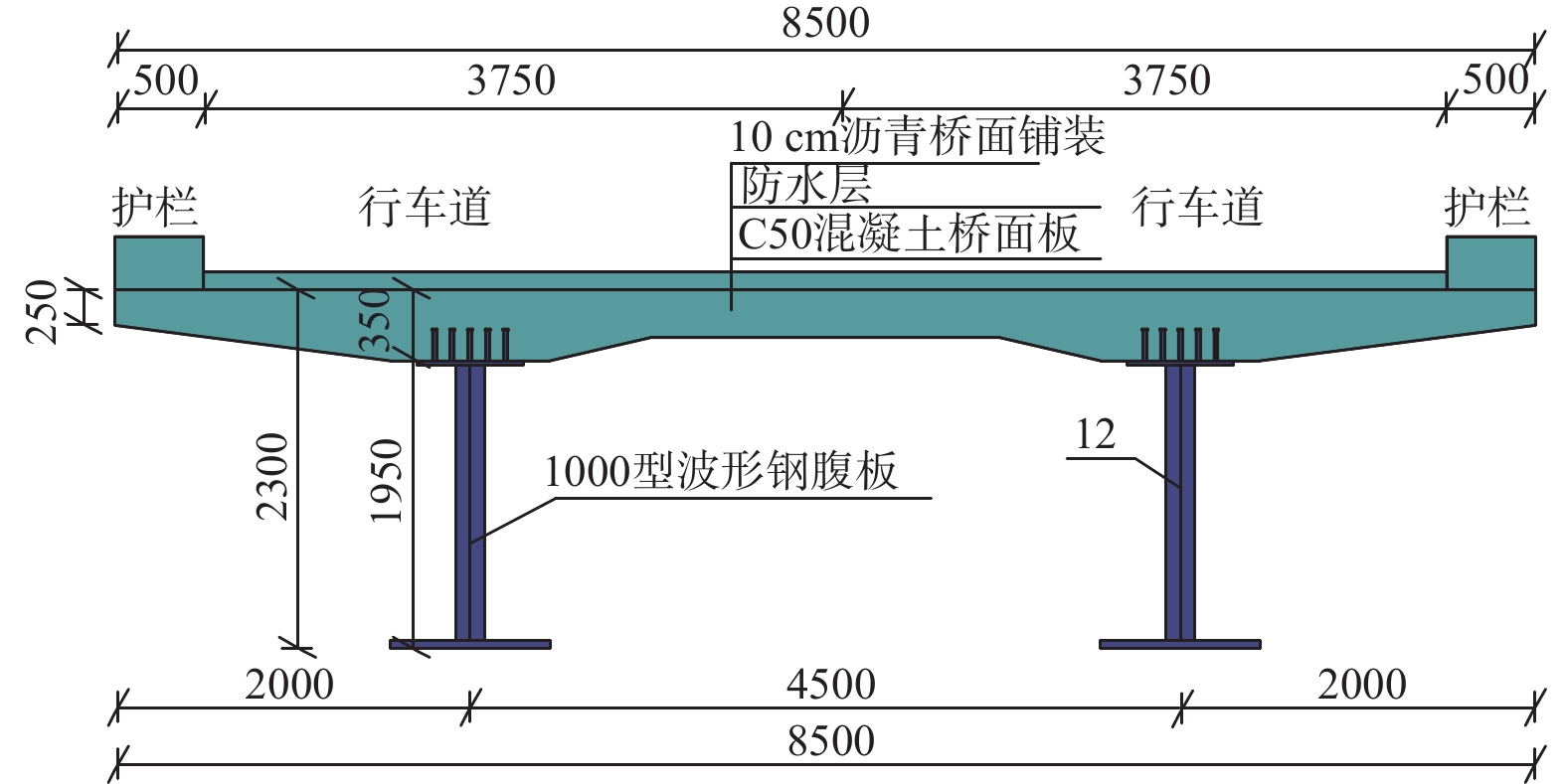
山东九龙东枢纽天桥为25 m+45 m+25 m三跨连续双主梁波形钢腹板工字钢-混组合板梁桥，主梁高2.3 m，外侧悬挑2 m。其中，桥面宽8.5 m，板厚350 mm；钢梁高1950 mm，采用Q355C钢材；上翼缘板宽800 mm，板厚25 mm；波形钢腹板采用1000型，腹板高1893 mm，板厚为12 mm；下翼缘板宽900 mm，板厚36 mm。预制桥面板通过集簇式栓钉与钢梁连接为整体，如图1所示。试验梁以此实桥为工程背景，遵循刚度等效以及中性轴相对位置不变的原则对其进行1/5缩尺。由此设计得到的两根试验梁整体尺寸一致，如表1所示，试验梁长为4200 mm，桥面板宽700 mm，厚度为150 mm，钢梁高385 mm，钢梁在支座及加载位置处布置加劲肋以增强截面稳定性。其中，桥面板内设有两层钢筋，直径为12 mm；钢梁上下翼缘板宽均为180 mm，厚度分别为10 mm、16 mm；上翼缘布置集簇式栓钉，栓钉横向间距50 mm，纵向间距80 mm，栓钉规格为Φ19×80；波形钢腹板高359 mm，厚度为5 mm。两组试验梁不同之处在于第1根试验梁(编号为CSRC)采用预制NC桥面板，槽孔处后浇混凝土与钢梁连接，第2根试验梁(编号为CSRCU)采用叠层桥面板，桥面板下层采用预制NC桥面板，上表面进行凿毛处理，上层及槽孔处后浇UHPC与钢梁连接，如图2所示。其中，常温养护型UHPC浇筑完成后，暴露于空气的部位需立即用养生薄膜覆盖进行持续3天以上的保湿养护，48小时后方可拆除模板。

试验所用UHPC为水泥、硅灰、粉煤灰、石英粉、石英砂、水和减水剂组成，其配合比为水泥∶硅灰∶粉煤灰∶石英粉∶石英砂∶水∶减水剂=1.00∶0.25∶0.10∶0.25∶1.10∶0.24∶0.027。实测C50混凝土立方体抗压强度f_cu为60.8 MPa；UHPC立方体抗压强度f_cu为141.5 MPa；钢材屈服强度f_y为385 MPa，极限强度f_u为551 MPa；HRB400钢筋屈服强度f_y为448 MPa，极限强度f_u为614 MPa。

图  1  标准尺寸图 　/mm

Figure  1.  Standard dimensions

下载: 全尺寸图片 幻灯片

表  1  试验梁构造参数

Table  1.  Test beam construction parameters

构件名称	钢梁尺寸/mm							桥面板尺寸/mm
	腹板 高	腹板 厚	上翼缘			下翼缘
			宽	厚		宽	厚	宽	厚
CSRC	359	5	180	10		180	16	700	150(NC混凝土)
CSRCU	359	5	180	10		180	16	700	150=上层50(UHPC)+ 下层100(NC混凝土)

下载: 导出CSV 

| 显示表格

图  2  试验梁构造图 　/mm

Figure  2.  Test beam structure diagram

下载: 全尺寸图片 幻灯片

1.2   试验梁加载及测试

试验采用200T油压千斤顶置于试验梁正上方，通过分配梁对组合梁跨中桥面板两点对称加载，纯弯段长800 mm。试验测试内容主要包括:荷载挠度关系、混凝土板和钢梁应变等。在组合梁支点、加载点和跨中正下方布置位移测点，并沿纵向分别布置应变测点于桥面板和钢筋笼，如图3所示。在跨中截面布置一圈应变片，用以测试加载过程中跨中桥面板和钢梁的应变分布情况。试验数据由TDS-530静态数据采集仪进行采集。先对梁施加30 kN的预加载力，检查传感器是否正常工作及试验装置安全性。正式加载由0 kN开始，传感器进行初读数；之后每30 kN为一个加载等级，持荷5 min，采集传感器数据。按荷载控制逐级加载至加载力不再上升后，改为位移控制，每2 mm为一级，直至试件完全破坏。

图  3  试验梁加载及测点布置

Figure  3.  Test beam loading and measuring point arrangement

下载: 全尺寸图片 幻灯片

2   试验结果与分析

2.1   试验过程及破坏特征

混凝土极限压应变按我国《混凝土结构设计规范》(GB 50010−2010)^[21]规定取值为3300 με；UHPC极限压应变参照《活性粉末混凝土结构技术规程》(DBJ43/T 325−2017)^[22]规定取值为4080 με，考虑钢材延展性要求，规定钢材极限拉应变ε_u=15 ε_y^[23]。钢材实测屈服强度f_y=385 MPa，弹性模量E为206 000 MPa，故钢材屈服应变ε_y约为1800 με，钢材极限拉应变ε_u为27 000 με。

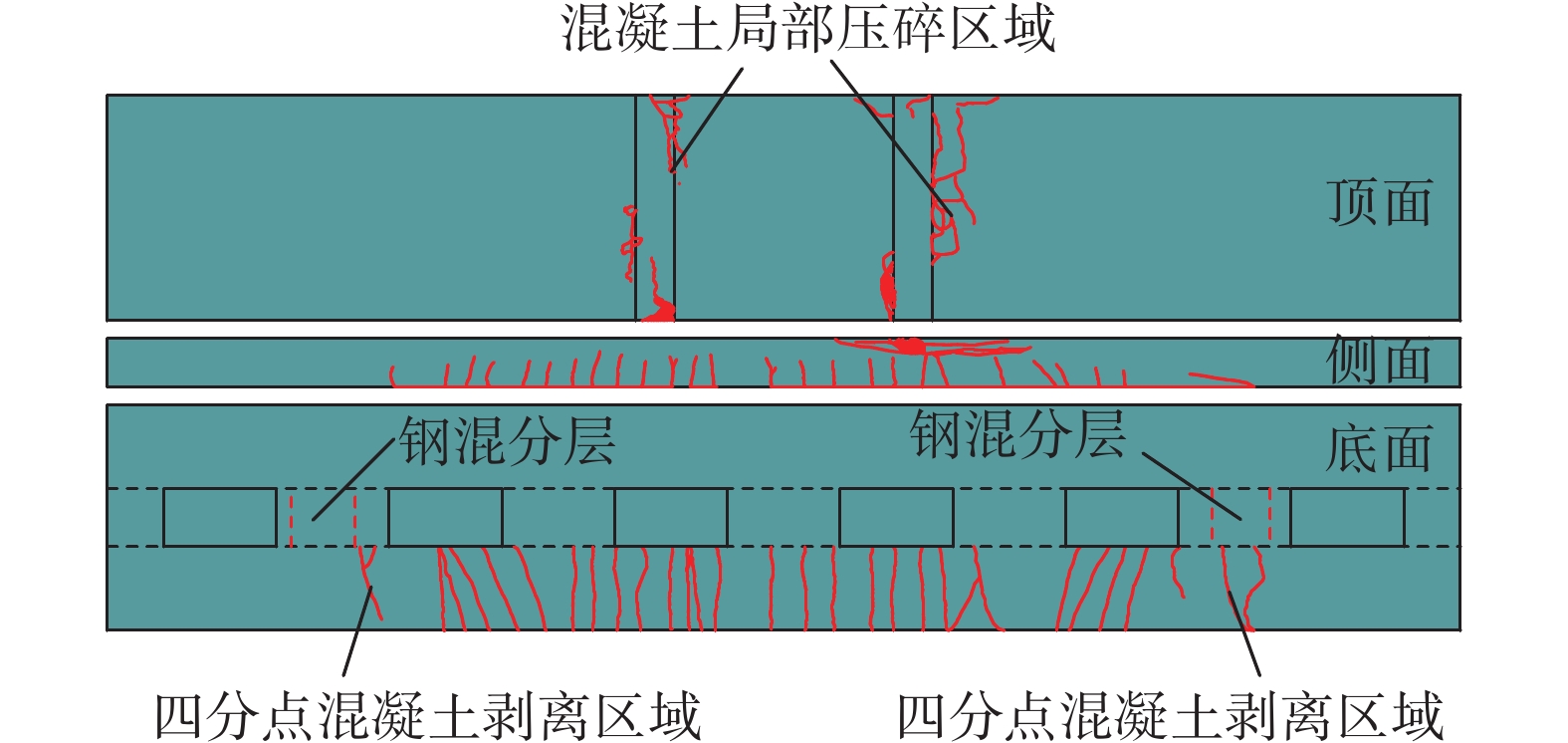
在加载初始阶段，钢梁与桥面板整体性良好，CSRC组合梁和CSRCU组合梁在荷载分别达到660 kN和720 kN时，钢梁下翼缘屈服。随着荷载的增加，跨中桥面板底部出现裂缝，挠度明显增加。当荷载加至1020 kN时，两组组合梁纯弯段桥面板底面横向裂缝延伸至侧面，CSRC组合梁四分点区段桥面板底面在从前后两槽孔中点位置处，混凝土小面积斜向剥离开裂，而CSRCU组合梁此处出现裂缝，但并未剥离。当荷载增至1116 kN时，CSRC组合梁钢梁下翼缘达到极限强度，加载端内侧桥面板顶面出现裂缝，且桥面板侧面边缘混凝土呈扇形压溃，荷载变化幅度较小并随后减小，此时试验梁已达到极限承载状态，停止加载。CSRCU组合梁在荷载加至1234 kN时，钢梁下翼缘达到极限强度，此时桥面板底面裂缝均发展至侧面，加载端桥面板顶面压裂。随后位移继续增加，但荷载变化幅度较小，当达到1250 kN后下降，此时加载端桥面板顶面及边缘UHPC层压溃，此时试验梁已达到极限承载状态，停止加载。两组试验梁桥面板与钢梁之间未发生掀起与错动，破坏及裂缝分布分别如图4和图5所示。

图  4  CSRC组合梁破坏形态

Figure  4.  Failure form of CSRC composite beam

下载: 全尺寸图片 幻灯片

图  5  CSRCU组合梁破坏形态

Figure  5.  Failure form of CSRCU composite beam

下载: 全尺寸图片 幻灯片

如图6、图7所示，两组试验梁都在跨中纯弯部分的侧面和底面出现了多条平行的裂缝，由于中性轴在混凝土板内，板侧面竖向裂缝并没有贯通，板底面横向裂缝均已贯通，桥面板顶面加载位置和侧面混凝土均被压碎，跨中挠度明显。波形钢腹板底部受力变形，虽然具有手风琴效应，但底部一定高度范围内依旧受纵向应力影响较大。与CSRC组合梁相比，CSRCU组合梁桥面板破坏范围小，剪跨区四分点槽孔间混凝土开裂但并未发生剥离现象，桥面板与钢梁并未分层。由于UHPC具有较高的抗压强度，以及内部钢纤维具有一定的阻裂作用，使得组合梁延性具有大幅度的提高，跨中波形钢腹板的变形范围更大。

图  6  CSRC组合梁试验破坏形态

Figure  6.  Test failure mode of CSRC composite beam

下载: 全尺寸图片 幻灯片

图  7  CSRCU组合梁试验破坏形态

Figure  7.  Test failure mode of CSRCU composite beam

下载: 全尺寸图片 幻灯片

2.2   荷载-位移曲线

图8为两组试验梁加载过程中的荷载-位移曲线，P_y、P_u分别为试验梁的屈服荷载和极限荷载，δ_y和δ_u分别为钢梁下翼缘屈服和试验梁达到极限状态时对应的位移。从图8中可以看出，两组试验梁的荷载-挠度曲线变化趋势基本相同，从开始受力到钢梁开始产生塑性变形，试验梁从弹性阶段转入弹塑性阶段，随后桥面板开裂标志着试验梁进入破坏阶段，直至桥面板压溃或钢梁下翼缘达到极限强度。

图  8  荷载-位移曲线

Figure  8.  Load-displacement curve

下载: 全尺寸图片 幻灯片

在弹性阶段，两组试验荷载-位移曲线都近似为直线，如表2所示，CSRC试验梁的屈服荷载为660 kN(约0.60 P_u)，对应挠度为11.7 mm，弹性刚度为56.4 kN/mm，CSRCU试验梁的屈服荷载为720 kN(约0.57 P_u)，对应挠度为11.3 mm，弹性刚度为63.7 kN/mm，UHPC由于弹性模量较大，对弹性阶段组合梁的刚度具有约13%的提升。在弹塑性阶段，钢梁达到屈服强度导致试验梁刚度下降，相同荷载下，CSRC试验梁挠度增长速度大于CSRCU试验梁。在破坏阶段，桥面板局部压溃，组合梁挠度增加较快，钢梁下翼缘达到极限强度，CSRC试验梁的极限承载力为1106 kN，对应挠度为82.2 mm，CSRCU试验梁的极限承载力为1254 kN，对应挠度为94.7 mm，与CSRC试验梁相比，承载力提高了13.4%。由极限承载力对应的挠度δ_u与屈服强度挠度δ_y比值可以发现CSRCU试验梁的延性较好。

表  2  试验结果对比

Table  2.  Comparison of test results

编号	屈服挠度 δy/mm	屈服荷载/ kN	极限挠度 δu/mm	极限荷载/ kN	延性系数 (δu/δy)
CSRC	11.7	660	82.2	1106	7.0
CSRCU	11.3	720	94.7	1254	8.4

下载: 导出CSV 

| 显示表格

2.3   荷载-应变曲线

2.3.1   桥面板应变

图9给出了两组组合梁桥面板的荷载-应变曲线。从图9中可以看出，桥面板受压区纵向应变增长幅度随着距离支点的距离的增加而逐渐变大，在纯弯段处的桥面板纵向应变随着荷载的增加先是呈线性缓慢增长，当钢梁下翼缘达到屈服强度后，增长速率迅速增加。从图9中可以看出，两组组合梁桥面板底面受拉应变随着荷载的增加逐步增长，两者均在钢梁下翼缘达到屈服强度后，桥面板底面混凝土开裂，混凝土受拉区退出工作。CSRC组合梁在极限荷载1106 kN的作用下，跨中混凝土纵向应变达极限压应变3300 με。CSRCU组合梁在极限荷载1254 kN作用下，压应变为3725 με，接近UHPC板极限压应变4080 με。

图  9  桥面板荷载-应变曲线

Figure  9.  Bridge deck load-strain curve

下载: 全尺寸图片 幻灯片

2.3.2   钢梁应变

图10 为两组试验梁钢梁的荷载-应变曲线，沿着跨中截面高度由上至下，纵向应变逐步增长。CSRC组合梁跨中钢梁截面高度130 mm(占腹板总高37%)范围内均达到屈服强度，CSRCU组合梁跨中钢梁全截面达到屈服强度，在各自极限荷载下，钢梁上翼缘纵向应变达到屈服应变，钢梁下翼缘均几乎达到极限拉应变27 000 με，钢材强化效应明显。

图  10  钢梁荷载-应变曲线

Figure  10.  Steel beam load-strain curve

下载: 全尺寸图片 幻灯片

总体来说，CSRC试验梁在极限承载力下，NC桥面板和钢梁下翼缘几乎都达到极限强度，CSRCU试验梁钢梁下翼缘达到极限状态，而UHPC叠合板还未达到极限强度，呈现出“UHPC叠合板强、钢梁弱”的特征，所以UHPC叠合板厚度不宜取太厚。

2.4   极限状态下跨中截面纵向应变

如图11所示，两组试验梁跨中截面纵向应变沿高度由上往下，由受压到受拉。CSRC、CSRCU组合梁波形钢腹板处于弹性阶段(0.6 P_u之前)时，受手风琴效应影响，靠近混凝土桥面板一定高度范围内波形钢腹板纵向应变非常小，只有接近下翼缘处波形钢腹板应变较大，但也远小于受拉钢翼缘板的应变，因此，弹性阶段忽略波形钢腹板的抗弯贡献。在极限荷载下，CSRC试验梁波形钢腹板顶端应变仍然较小，但腹板底端纵向应变达到6437 με，接近50%腹板高度范围内达到屈服应变，CSRCU试验梁腹板顶端纵向应变为1842 με，底端应变达到8207 με，沿腹板高度范围内均达到屈服应变，因此，波形钢腹板组合梁极限承载力不可忽略腹板的抗弯贡献。

图  11  跨中纵向应变沿截面高度分布

Figure  11.  Distribution of mid-span longitudinal strain along section height

下载: 全尺寸图片 幻灯片

3   有限元参数分析

3.1   模拟方式

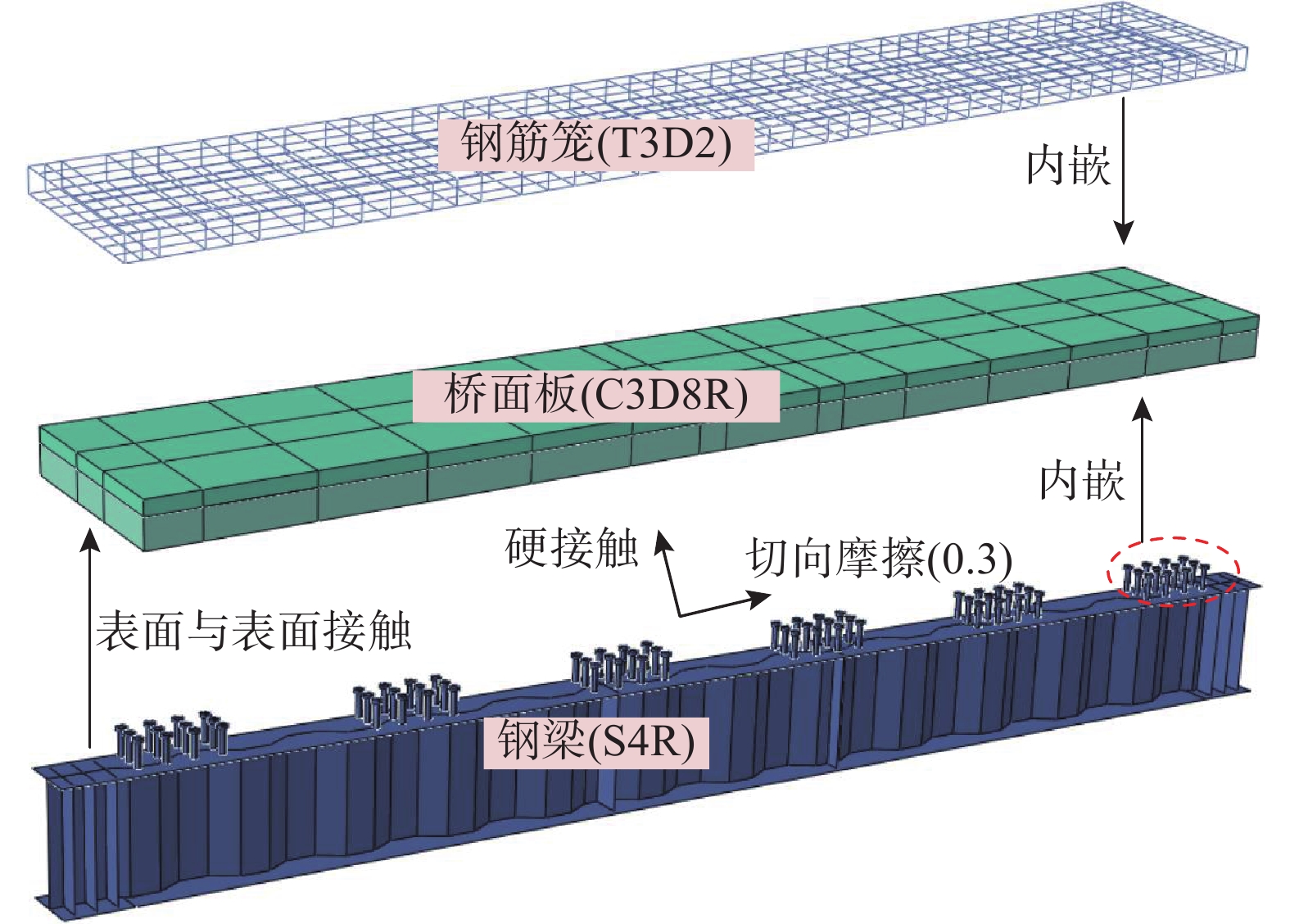
为分析组合梁在弹性至极限荷载作用下梁体的非线性行为，应考虑材料非线性、几何非线性等，采用有限元软件ABAQUS对模型梁的组成部分用不同单元进行模拟。其中桥面板、栓钉采用实体单元C3D8R模拟，钢梁采用壳单元S4R模拟，钢筋采用桁架单元T3D2模拟。在梁一端支座位置限制竖向自由度，另一端支座限制竖向自由度和水平自由度。钢梁与预制桥面板之间接触采用法向硬接触，切向无摩擦，而槽孔处的后浇混凝土与钢梁之间除硬接触外还需设置切向摩擦，摩擦系数取为0.3；普通钢筋和栓钉通过内嵌方式，实现与桥面板的连接；由于在试验加工过程中，UHPC叠层桥面板下层普通混凝土层表面进行凿毛，且上层和槽孔处全部后浇UHPC，极大地提高了UHPC层与NC层的粘结性，使两者成为一体，不会出现掀起错动的情况，因此有限元模型中对桥面板进行分割，根据材料不同赋予桥面板单元不同的材料属性，如图12所示。混凝土采用《混凝土结构设计规范》(GB 50010−2010)^[21]中的本构模型。UHPC的受压本构关系由式(1)~式(5)可得，受拉本构关系由式(6)~式(7)可得^[22]。钢材采用双线性随动强化材料模型^[23]，塑性阶段钢材刚度取初始刚度1/100，各材料参数均按实测值取值。

图  12  有限元模型

Figure  12.  Finite element model

下载: 全尺寸图片 幻灯片

式中：σ_c为压应变为ε_c时的压应力；f_c为轴心抗压强度设计值；f_cu,k为立方体抗压强度标准值；ε₀为UHPC峰值应力f_c对应的压应变；ε_cu为极限压应变。

式中：σ_t为拉应变为ε_t时的拉应力；f_t为轴心抗拉强度设计值；ε_t0为拉应力达到f_t时的拉应变；ε_tu为极限拉应变，可取1000 με。

3.2   模型验证

为验证有限元计算结果的准确性，按照上述建模方法与两组试验梁进行对比验证。如图13(a)所示，CSRC有限元与试验结果相比，极限荷载下跨中桥面板压应变为3425 με，达到极限强度,与试验梁桥面板压溃现象一致，屈服荷载和极限荷载相差分别为5%和2%，弹性阶段和塑性阶段刚度相差不大。如图13(b)所示，CSRCU有限元与试验结果相比，极限荷载下下翼缘拉应变为27 660 με，达到极限强度，屈服荷载和极限荷载相差分别为4%和1%，弹性阶段刚度几乎相同，塑性阶段有限元刚度略小。两组模型与试验梁破坏形式一致，有限元计算结果可以真实反应试验梁的受力状态。

图  13  数值模拟与试验结果对比

Figure  13.  Comparison of numerical simulation and experimental results

下载: 全尺寸图片 幻灯片

3.3   剪力连接度

从上述2.3节试验梁跨中截面纵向应变沿高度分布可知，在极限状态下，CSRC试验梁腹板接近50%高度范围内达到屈服强度，CSRCU试验梁腹板沿高度范围内均达到屈服强度。我国《钢-混凝土组合桥梁设计规范》(GB 50917−2013)^[24]规定各剪跨区段内剪力连接件的数目${n_{\text{f}}}$应达到以下要求：

式中：V_s为剪跨区桥面板与钢梁之间的纵向剪力；$N_{\text{v}}^{\text{c}}$为单个连接件抗剪承载力设计值；A_s为钢梁截面面积；f_d为钢材抗拉强度设计值；A_c为桥面板截面面积；f_cd为混凝土抗压强度设计值。

对于波形钢腹板工字钢组合梁而言，由于波形钢腹板的手风琴效应，设计时往往忽略波形钢腹板，使得钢梁相对于桥面板较弱，各剪跨区内钢梁与混凝土板之间的剪力由钢梁决定，若钢梁面积忽略波形钢腹板截面面积则会导致剪力连接件数量不足，从而使得设计偏于不安全。从上述2.3节试验梁跨中截面纵向应变沿高度分布可知，在极限状态下，CSRC试验梁腹板接近50%高度范围内达到屈服强度，CSRCU试验梁腹板沿高度范围内均达到屈服强度。因此，本文提出对于波形钢腹板-NC组合梁在计算剪力连接件数量时需考虑波形钢腹板50%的截面面积，而对于波形钢腹板-UHPC-NC组合梁而言，需考虑波形钢腹板全部截面面积。桥面板与钢梁之间的连接程度由剪力连接度r表示，其计算公式为：

式中：n为剪跨区连接件数量；n_f为保证桥面板或者钢梁能够进入塑性阶段所需的连接件数量。

按照此设计方法对两组试验梁进行剪力连接度参数分析，两组试验梁各建立7组模型(r分别为0.25、0.50、0.75、0.85、1.00、1.25和1.50)。如表2、表3所示，所有模型中均是栓钉最先发生屈服，随荷载的增大，屈服的栓钉数量不断增多，CSRC组合梁在0.25≤r≤0.85范围内时，栓钉全部屈服荷载小于钢梁下翼缘屈服荷载，栓钉在钢梁发生屈服之前已全部屈服，因此r≥0.85即可保证跨中钢梁下翼缘在全部栓钉屈服之前就已进入塑性阶段，组合梁即可满足完全抗剪的设计要求。CSRCU组合梁在0.25≤r≤0.75范围内时，栓钉在钢梁下翼缘屈服之前已全部屈服，因此对于CSRCU组合梁而言，满足r≥0.75即可保证钢梁先发生屈服，满足完全抗剪的要求。如图14(a)、图14(b)所示，CSRC和CSRCU组合梁在r≥0.85和r≥0.75后的弹塑性阶段的抗弯刚度和荷载增长幅度较小，因此，建议对于CSRC和CSRCU组合梁的剪力连接度的取值范围分别在0.85~1.00和0.75~1.00，可减少连接件数量，降低预制装配施工难度和提高结构的经济性。

表  3  CSRC有限元模型剪力连接度分析

Table  3.  Analysis of shear connectivity of CSRC finite element model

剪力连 接度r	栓钉全部 屈服荷载/kN	钢梁下翼缘 屈服荷载/kN	极限荷载/ kN	破坏 形式
0.25	200	657	720	栓钉剪断
0.50	445	677	975	栓钉剪断
0.75	574	681	993	桥面板压溃
0.85	685	684	999	桥面板压溃
1.00	723	686	1001	桥面板压溃
1.25	842	687	1009	桥面板压溃
1.50	987	687	1010	桥面板压溃

下载: 导出CSV 

| 显示表格

图  14  跨中荷载-位移曲线

Figure  14.  Mid-span load-displacement curve

下载: 全尺寸图片 幻灯片

表  4  CSRCU有限元模型剪力连接度分析

Table  4.  Analysis of shear connectivity of CSRCU finite element model

剪力连 接度r	栓钉全部 屈服荷载/kN	钢梁下翼缘 屈服荷载/kN	极限荷载/ kN	破坏形式
0.25	244	668	769	栓钉剪断
0.50	469	692	1044	栓钉剪断
0.75	694	694	1118	钢梁破坏
0.85	794	699	1144	钢梁破坏
1.00	868	702	1149	钢梁破坏
1.25	1019	703	1151	钢梁破坏
1.50	1044	703	1156	钢梁破坏

下载: 导出CSV 

| 显示表格

3.4   NC板厚和UHPC板厚的影响

在保证CSRCU试验梁抗弯性能能够满足条件的情况下，提出桥面板采用叠合板的合理板厚比，既能发挥超高性能混凝土UHPC优异的抗压、抗疲劳等性能，又能减少UHPC的用量。因此，叠合板在NC板与UHPC板的合理板厚比有待研究，需对其展开参数分析。保持桥面板厚h_w不变，取NC板厚度h_NC与UHPC板厚度h_U比值分别为0.50、0.67、0.88、1.14、1.50、2.00、2.75、4.00和5.00进行分析。由图15(a)、图15(b)可知，随着h_NC/h_U数值的增加，弹性刚度以及屈服荷载变化较小。极限荷载P_u随着UHPC的厚度的减小逐渐减小，当h_NC/h_U在0.50~2.75范围内时，极限承载力下降程度较小，承载力相差不大，所以UHPC板厚度h_U无需取得太大，因此叠层板NC板与UHPC板的合理板厚比主要根据经济性考虑。而当h_NC/h_U达到2.75后极限承载力下降幅度较大，且组合梁破坏模式由钢梁破坏转为UHPC层压溃。虽然h_NC/h_U在0.50~1.50时，UHPC层较厚，组合梁呈现“UHPC强，钢梁弱”的特征，钢梁发生破坏，UHPC材料并没有利用充分，而当UHPC层的厚度太小(h_NC/h_U>4)会影响叠合板中NC板与UHPC板的组合效应，对施工造成不便。因此，基于抗弯性能相差不大及经济性考虑，建议h_NC/h_U取值在1.50~2.75范围内。

图  15  NC板厚和UHPC板厚对CSRCU组合梁的影响

Figure  15.  Influence of NC plate thickness and UHPC plate thickness on CSRCU composite beam

下载: 全尺寸图片 幻灯片

3.5   UHPC叠层等效厚度

由于CSRCU组合梁表现出较高的刚度、承载力和延性，因此保持h_NC/h_U比值为2不变，减小叠合板厚度分别为90 mm、100 mm、110 mm、120 mm和130 mm进行分析。由图16(a)、图16(b)所示，当桥面板厚度减薄到120 mm时，与桥面板厚度为150 mm的CSRC组合梁相比，极限承载力几乎相同，弹性刚度相差11%。可见对于采用UHPC的叠合梁桥面板而言，其厚度可以相比于全NC桥面板减薄20%左右，减轻桥梁自重。

图  16  叠合板等效厚度

Figure  16.  Equivalent thickness of laminated plate

下载: 全尺寸图片 幻灯片

4   结论

本文通过试验和数值分析研究了采用叠合板形式的波形钢腹板工字钢组合梁的弯曲性能，并给出了构造设计参数的合理取值建议，具体结论如下：

(1) CSRCU组合梁与CSRC组合梁破坏模式均为典型的弯曲破坏，UHPC高强度的特点使得CSRCU试验梁桥面板破坏范围较小，且槽孔处采用UHPC保证了钢混不分层，延性更好，与CSRC组合梁相比，弹性刚度和极限承载力均提高了13%左右。

(2)在极限状态下，桥面板与钢梁上下翼缘应变呈线性分布符合平截面假定，CSRCU组合梁波形钢腹板沿截面高度范围内均达到屈服强度，CSRC组合梁波形钢腹板靠近钢梁上翼缘一侧应变较小，而靠近钢梁下翼缘一侧已进入钢材强化阶段，并且腹板约50%高度范围内达到屈服强度，波形钢腹板抗弯贡献不可忽略不计。在计算组合梁剪力连接度时，CSRCU组合梁钢梁需考虑波形钢腹板全部截面面积，CSRC组合梁需考虑50%腹板截面面积，为减少连接件数量以便于施工，两者剪力连接度分别达到0.75和0.85即可满足受力要求。

(3)在保证结构受力的前提下，提高经济性，建议CSRCU组合梁NC层与UHPC层厚度比取值在1.50~2.75范围内。

(4)相比于NC桥面板，UHPC-NC叠合板厚度可以减薄20%，以减轻结构自重，提高波形钢腹板组合梁桥跨径。