RANDOM SEISMIC RESPONSE ANALYSIS OF GRAVITY DAM CONSIDERING INFLUENCE OF COMPLEX WAVEFIELD
-
摘要:
针对重力坝随机地震响应分析尚未有效考虑复杂波场影响的问题，该文提出场址波场的随机模拟方法并对重力坝的随机地震响应开展研究。为确保入射波对场地的代表性，以场地谱为目标完成复杂入射波场的生成和调整。采用非一致波动输入模型实现考虑地基辐射阻尼的复杂波场输入，并以向家坝工程左岸非溢流坝段为例给出复杂波场影响下的重力坝随机地震响应分析成果。结果显示，波场随机模拟方法可提供适合重力坝随机地震响应分析需要的波场信息。在设计峰值地震动对应的随机波场影响下，向家坝非溢流坝段的坝踵第一主应力峰值均值为1.93 MPa，均方差为0.594 MPa，变异系数0.307；下游坝面的第一主应力峰值均值为1.37 MPa，均方差为0.336 MPa，变异系数0.257。算例中坝踵第一主应力峰值的变化范围为1.02 MPa~2.95 MPa，依据正态分布得到坝踵单元受拉破坏的概率为0.281%。
Abstract:Complex wavefields are not effectively considered in the random seismic response analysis of high-gravity dams. The random wavefield method generating the incident waves at the project site is proposed and the random seismic response analysis of the gravity dam is performed in this paper. To ensure the representativeness of the wavefield to site conditions, the wave information is generated and adjusted by comparing the response spectrum of the corresponding horizontal acceleration’s response spectrum at the reference point and the target spectrum. The non-uniform wave input method is utilized to realize the input of complex wavefields and the radiation damping of the foundation. A non-overflow dam section in Xiangjiaba gravity dam is chosen as an example to perform investigations considering the complex wavefield. The results show that the random wavefield method can provide incident waves fit for random seismic response analysis of gravity dams. Under the influence of complex wavefield corresponding to the design ground acceleration, the mean peak of major principal stress at the dam heel is 1.93 MPa, with the MSE 0.594 MPa and the variation coefficient 0.307. The mean peak of major principal stress at the downstream slopeface is 1.37 MPa, with the MSE 0.336 MPa and the variation coefficient 0.257. In these cases, the peaks of major principal stress at the dam heel are from 1.02 MPa to 2.95 MPa, which indicates that the failure probability of the dam heel element is 0.281%, according to the normal distribution of peak response.
-
目前我国百米以上重力坝中30余座位于西南地区，典型工程如澜沧江流域的黄登(203 m)、雅砻江流域的官地(168 m)、金沙江流域的向家坝(162 m)等。受西南地区广泛分布的断裂带影响，重力坝建设和运行须解决的关键问题之一是确保其抗震安全。强震过程中，震源破裂过程和传播介质均存在较多不确定性因素，造成场址的地震动[1]和入射波[2]通常具有较强的随机性，从而引起重力坝结构地震响应出现变异。因此，对重力坝结构开展随机地震响应分析，了解响应的平均水准和变异情况是十分必要的。
重力坝地震响应分析通常基于振动输入[3]或波动输入[4 − 11]开展。振动输入以地面运动加速度为基础，将加速度时程转化为结构上的惯性力完成输入，此时地震动输入的随机性由加速度时程的时频域特征体现[12 − 15]。重力坝结构的随机地震响应需要数量较多的地面运动加速度时程，一般以目标谱为基础通过人工方法或筛选实测地震记录获取[16 − 17]。目前重力坝随机地震响应分析较多采用振动输入方法，如何蕴龙等[18]基于金井清谱发展考虑两向地震动的随机地震动模型，并研究重力坝随机地震响应的均值和变异系数；张社荣等[19]基于结构性能出发，从概率视角研究重力坝的随机地震响应；LUPOI和CALLARI[20]基于蒙特卡罗方法对Kasho重力坝的随机地震响应开展分析；其它相关研究数量较多[21 − 23]，不再详述。
波动输入以场址入射波和能量吸收边界为基础，将垂直或倾斜入射的地震波转化为边界节点力完成输入[24 − 25]。由于可模拟地震波的物理传播过程和地基辐射阻尼现象，波动输入更适合大型结构，尤其是大坝结构地震响应分析的使用[24 − 29]。从物理视角来看，场址强震动由复杂波场形成，因此，波动输入对随机性的表达应体现在波场信息上。在波场特征研究方面，何卫平分别从定性[30]和定量[31]角度论证了场址入射地震波为复杂波场，并拓展波动输入的入射波假定，发展出能有效表达地面运动的时间滞后、峰值变化和时程形状差异等特征的非一致波动输入模型[32 − 33]。然而，目前对场址波场信息的确定性研究仅能在理想化条件下开展，受震源破裂过程和传播介质无法定量评估影响，对具体工程场址的复杂波场信息的确定性研究仍无法实现，这也导致基于波动输入的大坝随机地震响应分析尚未有效开展。
综上，为推动波动输入在重力坝随机地震响应分析中的应用发展，本文结合大坝震损案例揭示的震源和场址特征，提出获得特定场址入射波信息的随机波场模型。为保证随机波场信息能用于重力坝结构地震响应分析，通过建立入射波与两向地面运动的联系，实现对复杂波场信息的生成和调整，使复杂波场对应的水平向地面运动的反应谱与场地谱吻合。然后，以非一致波动输入实现考虑地基辐射阻尼的复杂波场输入，并以向家坝工程典型非溢流坝段为例，开展考虑复杂波场影响的随机地震响应分析。
1 场址复杂入射波场的随机模拟
1.1 场址入射波特征分析
依据波动输入开展重力坝随机地震响应分析，须首先研究场址的入射地震波特征。
由理想条件下震源地震波的空间演化可知[31]，受传播介质复杂性影响[34 − 35]，单一震源地震波在场址形成的入射波为体波，呈现出数量庞大和信息复杂的特征。而真实的震源破裂过程可能形成极为复杂的震源地震波，由此推演，真实地震在场址形成的入射波必然是在幅值、入射角和到时等方面具备极大差异性的复杂波场。另外，不可忽视的因素是震源破裂过程和传播介质中也存在较多随机因素，将会进一步增加场址波场的复杂度，也阻碍获取场址入射波场的确定性信息。
受震源破裂过程和传播介质信息难以定量评估影响，现阶段基于确定性理论研究场址复杂波场仍面临较多限制。为满足工程结构地震响应分析对复杂波场的需求，本文从随机理论研究角度出发提出场址复杂入射波场的随机模拟方法。
1.2 场址入射波场的随机模拟
本节结合文献[31]揭示的场址入射波场特征，发展场址复杂入射波场的随机模拟方法。该方法基于以下假设：1)体波假设，该假设源于空间演化分析得到的近源场址入射波特征[31]，二维情况下默认为P波和SV波；2)平面波假设，该假设源于工程场址相对地震影响范围属小尺度[36 − 37]，即在场址范围内将入射波均视为平面波；3)均匀半无限空间假设，该假设默认场址入射波场的赋存介质为平面半无限空间，此时可依据波动理论建立入射波与两向地面运动的解析关系。基于以上先决条件，波场的随机模拟方法具体步骤如下：
1)依据目标谱生成地面运动水平分量的幅值和频率信息，其中幅值信息假定为满足区间(0, 1)的均匀分布，频率满足对数正态分布，分布参数依据目标谱调整；2)依据地面运动幅值信息结合随机方法生成入射波的性质，若水平运动分量的数值大于最大幅值的一半，将其设定为SV波，其它情况随机设定为SV波或P波；3) 假设P波和SV波的入射角满足在一定范围内均匀分布，随机生成P波和SV波的入射角，P波的入射角范围取值为5°~45°，SV波的入射角范围为0到临界角；4) 依据地震波性质、入射角和地面运动水平分量，获得入射波的幅值；5) 在到时方面，当地面运动水平分量的幅值大于最大值的一半，则假定该入射波的到时在时程的中间部分，其它情况则假定入射波的到时在全时程中均匀分布，将地震动时程设定为10.2 s，中间部分位于3 s~7 s之间。
对上述步骤得到的入射波场，叠加入射波和反射波可得到两向地面运动的解析解，具体计算公式可参考文献[32]。由于得到的水平向地面运动可能与工程需求存在偏差，因此仍需对复杂波场信息进行相应调整，该过程不再详述。
1.3 随机波场与地面运动
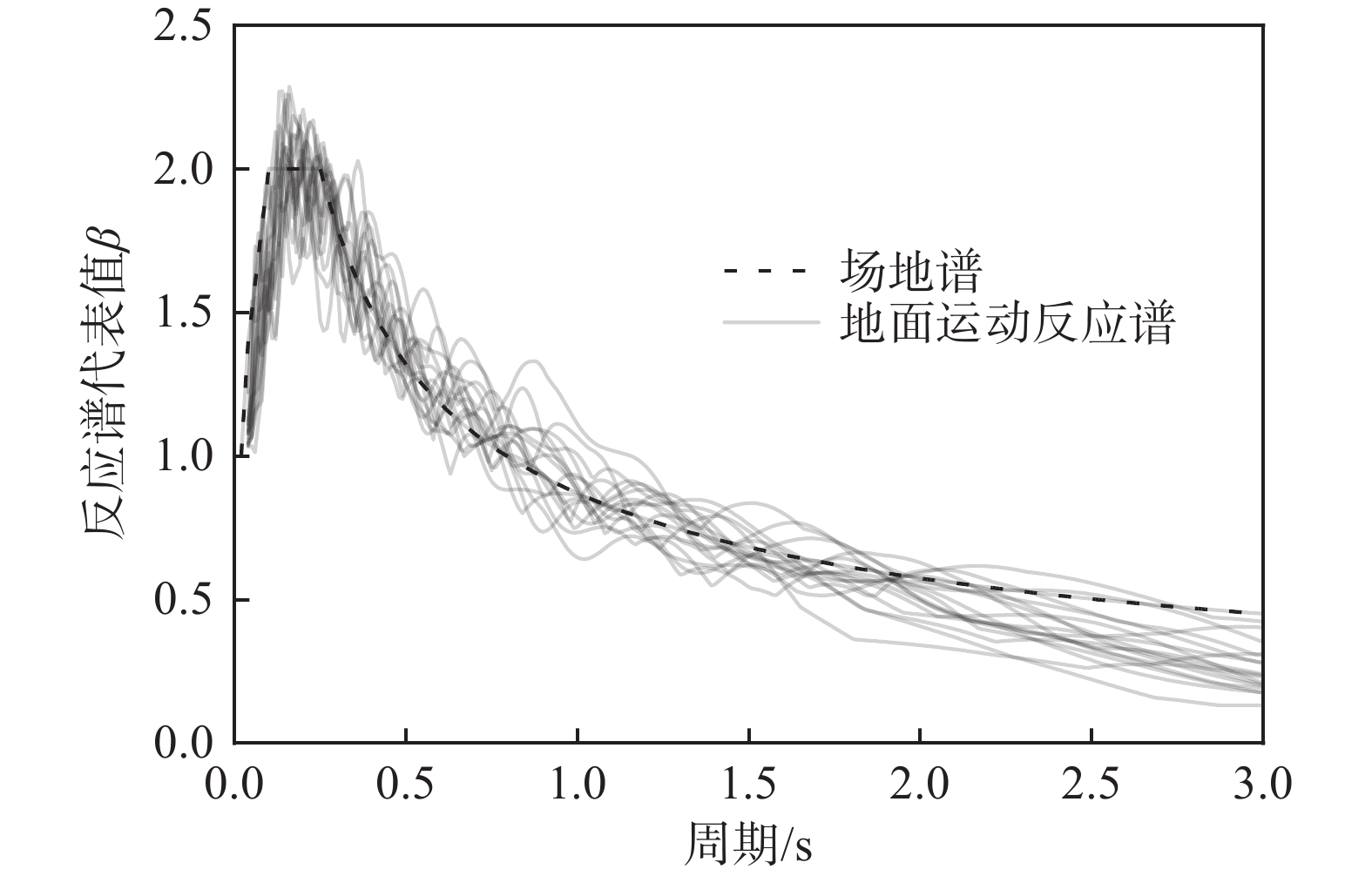
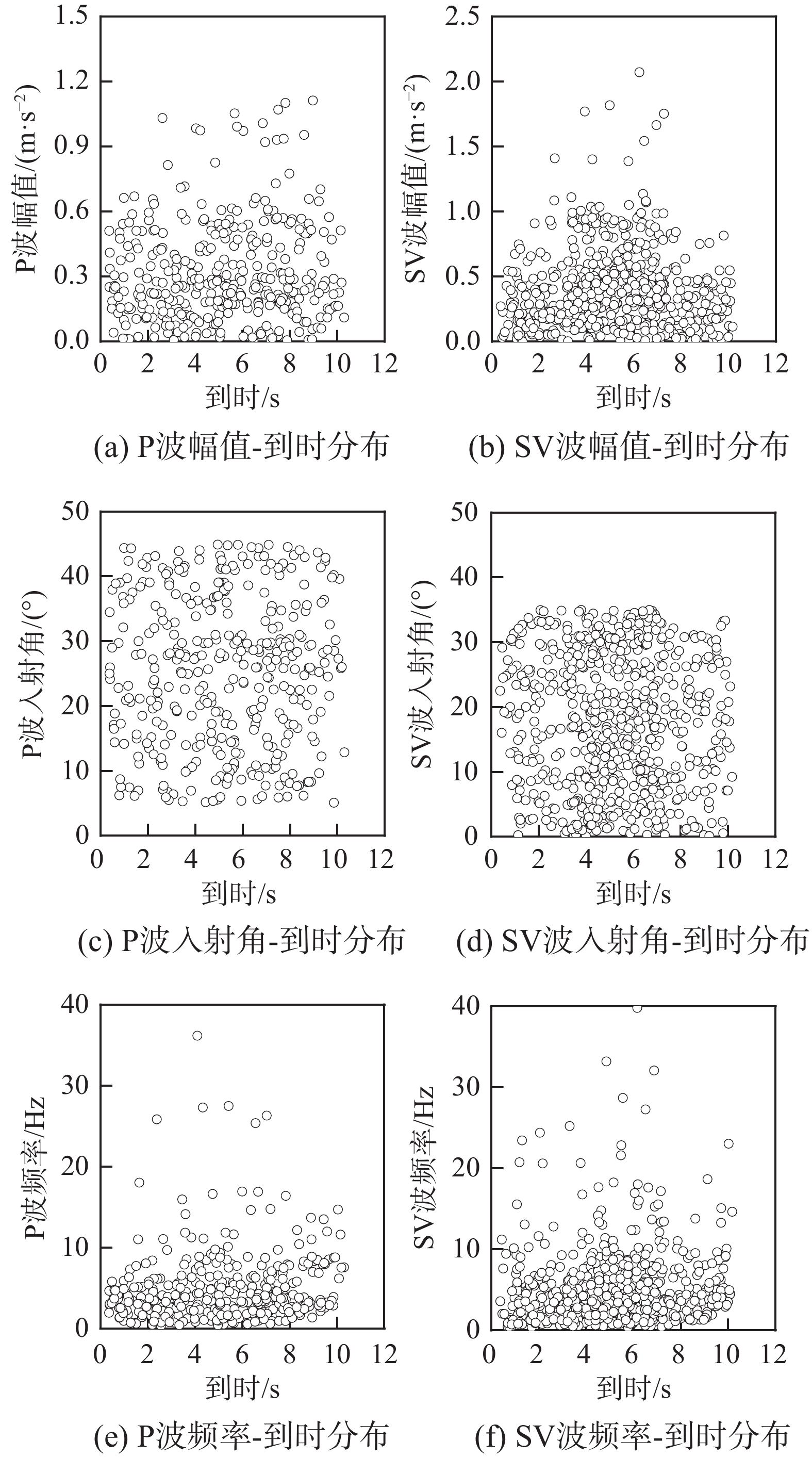
本文以向家坝工程的场地谱为目标生成随机波场，参数为T1=0.1、Tg=0.25、βmax=2.0。生成随机波场时，假设参考点水平向地面运动的频谱服从对数正态分布，其频率均值和均方差依据场地谱特征确定为5 Hz。研究中共生成18组随机波场信息，其中1例波场信息在图1显示，图中对入射P波和入射SV波分别展示，包含幅值、入射角和频率随到时的分布。
由随机波场信息可得到参考点地面运动的解析解，需要注意的是，由图1波场信息得到的参考点水平向加速度峰值与工程场址的水平向设计地震动峰值一般存在差异，此时须依据二者比值对波场幅值信息进行统一调整。1个算例参考点的两向地面运动加速度时程在图2显示。由图可知，由复杂波场得到的加速度时程的特征与实测地震动时程具备较强的相似度。在复杂波场对地面运动时程的具体影响方面，入射波的幅值和到时信息影响地面运动的峰值和时程形状，入射波的入射角影响两向地面运动的分量关系，入射波的频率影响地面运动的频谱信息。
![]()
图 2 某算例参考点两向地面运动Figure 2. Two-component ground accelerations at reference point in one case18个算例得到的参考点地面运动反应谱在图3显示，由图3可知，场址波场的随机模拟方法可有效获得场址的复杂入射波场信息，并确保参考点水平向运动的反应谱与场地谱基本一致。这说明最终得到的复杂波场信息可用于向家坝重力坝地震响应分析。
![]()
图 3 场地谱与参考点水平向加速度反应谱Figure 3. Site spectrum and response spectrums of horizontal acceleration at reference point2 复杂波场的输入实现
2.1 复杂波场的输入实现
重力坝地震响应计算中，复杂波场的输入以非一致波动输入实现[32 − 33]，该模型以粘弹性边界模拟地基辐射阻尼效应，叠加入射波及反射波在截断边界的节点力，实现复杂入射波场的输入，边界节点的平衡方程可表示为：
\begin{split} & \left[ \begin{matrix} {{{\boldsymbol{m}}_{xx}}}&0 \\ 0&{{{\boldsymbol{m}}_{{\textit{z}}{\textit{z}}}}} \end{matrix} \right]\left\{ \begin{matrix} {{{{\boldsymbol{\ddot u}}}_x}} \\ {{{{\boldsymbol{\ddot u}}}_{\textit{z}}}} \end{matrix} \right\} + \left[ \begin{matrix} {{{\boldsymbol{c}}_{xx}} + \Delta {{\boldsymbol{c}}_{xx}}}&{{{\boldsymbol{c}}_{x{\textit{z}}}}} \\ {{{\boldsymbol{c}}_{{\textit{z}}x}}}&{{{\boldsymbol{c}}_{{\textit{z}}{\textit{z}}}} + \Delta {{\boldsymbol{c}}_{{\textit{z}}{\textit{z}}}}} \end{matrix} \right]\left\{ \begin{matrix} {{{{\boldsymbol{\dot u}}}_x}} \\ {{{{\boldsymbol{\dot u}}}_{\textit{z}}}} \end{matrix} \right\}{\text{ + }} \\ &\qquad \left[ \begin{matrix} {{{\boldsymbol{k}}_{xx}} + \Delta {{\boldsymbol{k}}_{xx}}}&{{{\boldsymbol{k}}_{x{\textit{z}}}}} \\ {{{\boldsymbol{k}}_{{\textit{z}}x}}}&{{{\boldsymbol{k}}_{{\textit{z}}{\textit{z}}}} + \Delta {{\boldsymbol{k}}_{{\textit{z}}{\textit{z}}}}} \end{matrix} \right]\left\{ \begin{matrix} {{{\boldsymbol{u}}_x}} \\ {{{\boldsymbol{u}}_{\textit{z}}}} \end{matrix} \right\} = \left\{ \begin{matrix} {{{\boldsymbol{f}}_x}} \\ {{{\boldsymbol{f}}_{\textit{z}}}} \end{matrix} \right\} \\[-1pt] \end{split} (1) 式中：下标x和z为水平向和竖直向；m、c、k为边界节点的初始质量矩阵、阻尼矩阵和刚度矩阵；Δc、Δk为粘弹性边界对边界节点阻尼和刚度的修正；u、 {\boldsymbol{\dot u}} 和 {\boldsymbol{\ddot u}} 为节点运动的位移、速度和加速度向量；fx和fz为非一致波动输入对应边界节点力向量。
对于边界节点力，在侧边界为：
{{\boldsymbol{f}}_x}{\text{ = }}\sum\limits_{j = 1}^n {{\boldsymbol{\sigma A}}} + \Delta {{\boldsymbol{c}}_{\text{N}}}{{\boldsymbol{\dot w}}_x}{\text{ + }}\Delta {{\boldsymbol{k}}_{\text{N}}}{{\boldsymbol{w}}_x} (2) {{\boldsymbol{f}}_{\textit{z}}}{\text{ = }}\sum\limits_{j = 1}^n {{\boldsymbol{\tau A}}} + \Delta {{\boldsymbol{c}}_{\text{T}}}{{\boldsymbol{\dot w}}_{\textit{z}}}{\text{ + }}\Delta {{\boldsymbol{k}}_{\text{T}}}{{\boldsymbol{w}}_{\textit{z}}} (3) 在底边界为：
{{\boldsymbol{f}}_x}{\text{ = }}\sum\limits_{j = 1}^n {{\boldsymbol{\tau A}}} + \Delta {{\boldsymbol{c}}_{\text{T}}}{{\boldsymbol{\dot w}}_x}{\text{ + }}\Delta {{\boldsymbol{k}}_{\text{T}}}{{\boldsymbol{w}}_x} (4) {{\boldsymbol{f}}_{\textit{z}}}{\text{ = }}\sum\limits_{j = 1}^n {{\boldsymbol{\sigma A}}} + \Delta {{\boldsymbol{c}}_{\text{N}}}{{\boldsymbol{\dot w}}_{\textit{z}}}{\text{ + }}\Delta {{\boldsymbol{k}}_{\text{N}}}{{\boldsymbol{w}}_{\textit{z}}} (5) 式中：A为边界节点的影响范围；w和 {\boldsymbol{\dot w}} 为自由场条件下单个地震波引起边界节点的位移和速度；σ和τ为自由场条件下单个地震波在边界节点引起的法向应力和切向应力，计算公式可参阅文献[32]；n为复杂波场中入射地震波的数量；j为复杂波场中入射地震波的编号；ΔcN和ΔcT为粘弹性边界在法向和切向的阻尼修正；ΔkN和ΔkT为粘弹性边界在法向和切向的刚度修正，可参阅文献[38]取值。
2.2 非一致波动输入误差
为展示非一致波动输入对复杂入射波场的表达，将得到的参考点两向运动与解析解对比示于图4。图4显示，非一致波动输入得到的参考点加速度、速度和位移时程均与解析解保持一致。在加速度峰值方面，参考点解析解的两向运动峰值分别为−2.1778 m/s2和−1.8091 m/s2，非一致波动输入得到的峰值分别为−2.2595 m/s2和−1.8086 m/s2，误差分别为3.75%和0.03%。在速度峰值方面，参考点解析解的两向运动峰值分别为21.43 cm/s和20.07 cm/s，非一致波动输入得到的峰值分别为21.59 cm/s和19.75 cm/s，误差分别为0.75%和1.59%。在位移峰值方面，参考点解析解的两向运动峰值分别为−8.749 cm和−6.066 cm，非一致波动输入得到的峰值分别为−8.750 cm和−6.065 cm，误差分别为0.01%和0.02%。
![]()
图 4 非一致波动输入参考点地面运动Figure 4. Ground motion at the reference point by non-uniform wave input method由误差数据分析可知，非一致波动输入在模拟地面运动方面具备较高的精度，加速度的最大误差为3.75%，速度的最大误差为1.59%，位移的最大误差为0.02%。该现象的原因是特定尺寸的有限元网格在模拟低频运动时精度较高，在模拟高频运动时精度较低，而运动中的频率由低到高为位移、速度和加速度，因此模拟结果中位移的误差最小，速度稍大，加速度最大。总体而言，数值模拟中地面运动的误差均小于5%，说明非一致波动输入可在保证地面运动精度前提下实现场址复杂入射波场的输入。其余算例的参考点运动情况类似，此处不再展示。
3 重力坝随机地震响应评估
3.1 重力坝有限元模型和材料参数
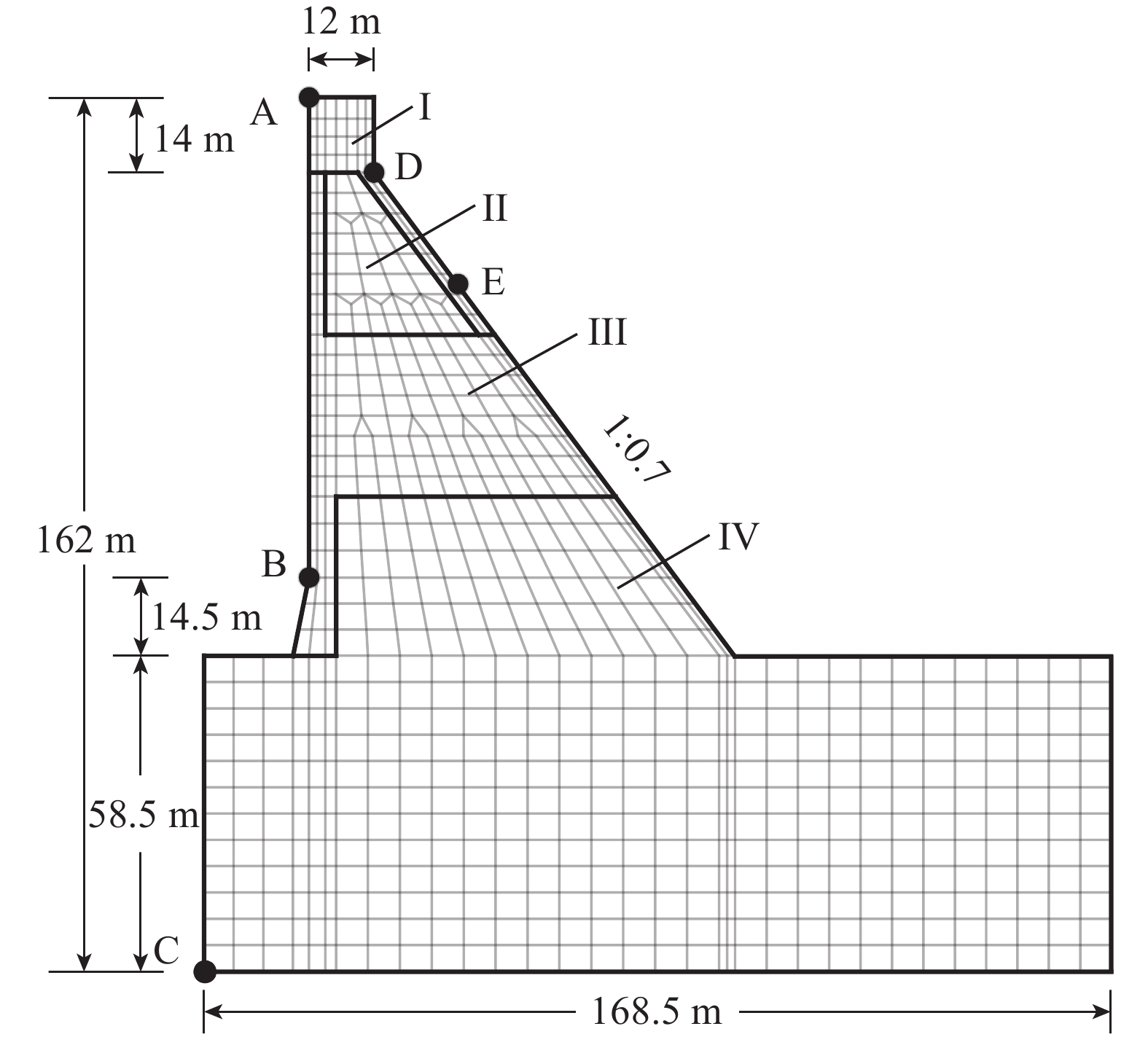
考虑复杂波场影响的重力坝随机地震响应分析以向家坝工程为例开展研究，该工程位于金沙江流域，控制流域面积45.88万km2，电站装机容量775 万kW，场址水平向设计地震加速度峰值为0.222 g。工程由左岸至右岸分别包含左岸非溢流坝段、冲沙坝段、厂房坝段、溢流坝段、右岸非溢流坝段。研究选定左岸非溢流坝段3#，坝段高度162 m，正常蓄水位水深158 m。工程建设过程中，为满足施工度汛泄洪需求，对该坝段建基面以上38 m处设计导流底孔，建成后对底孔进行封堵，最终形成底部为方形基座的非溢流坝段(图5)。
![]()
图 5 向家坝非溢流坝段有限元模型Figure 5. Finite element model of non-overflow monolith in Xiangjiaba gravity dam依据坝段信息建立的有限元模型中，坝体采用平面应力单元模拟，网格在图5显示。图中坝顶(A)、上游折坡(B)、坝踵(C)、下游折坡(D)和下游坝面(E)是研究关注的5个特征位置。地基采用平面应变单元模拟，在上下游和底部均取为2倍坝高。
坝体的材料分区在图5显示，坝体和地基的材料参数在表1显示。采用Rayleigh阻尼模型，阻尼系数以模型前2阶自振频率和阻尼比0.05确定。
表 1 坝体和地基材料参数Table 1. Parameters of dam concrete and foundation材料区域 弹性模量/GPa 泊松比 密度/(kg·m−3) 坝体 I区 42.00 0.167 2550 II区 26.25 0.167 2550 III区 38.25 0.167 2550 IV区 42.00 0.167 2550 地基 12.00 0.250 2600 计算中考虑的荷载包含坝体自重、上下游面静水压力、扬压力、动水压力和地震荷载。动水压力采用Westguarrd附加质量表示，计算公式为：
{m_i} = 0.875\rho {A_i}\sqrt {{H_0}{y_i}} (6) 式中：m为坝体上游面节点的附加质量；ρ为水体密度，取为1000 kg/m3；A为坝体上游面节点的影响范围；y为坝体上游面节点对应的深度；H0为上游库水深度；i为坝体上游面的节点编号。
3.2 重力坝响应均值分布
以波场随机模拟方法生成的18例波场为基础，计算向家坝典型非溢流坝段的随机地震响应。
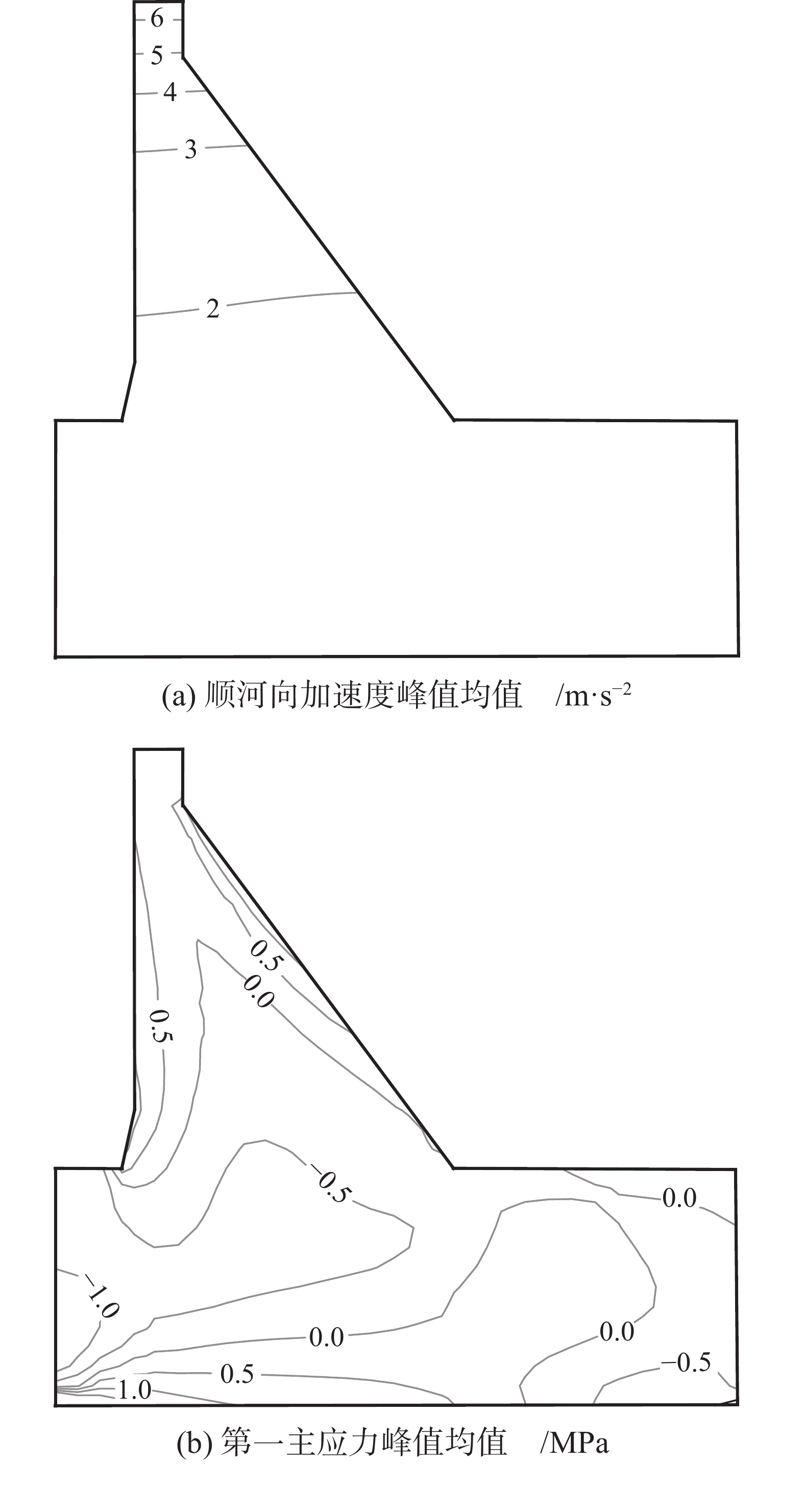
图6为坝体顺河向加速度和第一主应力响应的峰值均值分布。坝体顺河向加速度等值线呈水平分布，加速度的峰值均值从坝底向坝顶逐渐增加，受鞭梢效应影响在坝顶部位达到最大。在具体数值方面，坝踵加速度的峰值均值为1.58 m/s2，坝顶加速度的峰值均值为6.56 m/s2。坝顶顺河向加速度峰值均值相对水平向设计地震动峰值放大约3.0倍。
坝体在上游面折坡及以上部位、坝踵、下游面折坡及以下部位的第一主应力峰值均值较大。受上游面水荷载和地震往复荷载的共同作用影响，在坝踵处的第一主应力数值最大，特征位置C的第一主应力峰值均值为1.93 MPa。在上游坝面折坡部位，第一主应力稍小于坝踵，特征位置B的第一主应力峰值均值为1.08 MPa。在下游面折坡部位，由于坝头较小导致的振动效应不显著，该部位的第一主应力峰值为0.84 MPa，小于临近的下游坝面，即在下游折坡部位向下约20 m高程的E位置，第一主应力峰值均值为1.37 MPa。
3.3 特征部位响应的变异性
本部分展示坝体特征位置地震响应的随机特征，主要响应量包含坝顶(A)的加速度和相对位移，上游折坡B、坝踵C、下游面折坡D和下游坝面E(图3)的第一主应力，其中坝顶的相对位移以坝顶节点位移减去坝踵位移获得，相关成果在表2显示。
表 2 重力坝特征位置的随机地震响应Table 2. Random response of gravity dam at chosen poisitons响应量 位置 最大值 最小值 均值 均方差 变异系数 水平向加速度
峰值/(m·s−2)A 7.94 5.57 6.56 0.672 0.103 相对位移峰值/cm A 6.40 4.33 5.07 0.660 0.130 第一主应力
峰值/MPaB 1.71 0.63 1.08 0.345 0.319 C 2.95 1.02 1.93 0.594 0.307 D 1.21 0.48 0.84 0.216 0.257 E 1.94 0.86 1.37 0.336 0.245 坝顶加速度峰值的范围在5.57 m/s2和7.94 m/s2之间，均值为6.56 m/s2，均方差为0.672 m/s2。坝顶相对位移峰值的范围在4.33 cm和6.40 cm之间，均值为5.07 cm，均方差为0.660 cm。
在坝体应力方面，受水荷载和地震往复荷载共同影响，坝踵的第一主应力峰值较大，峰值范围在1.02 MPa和2.95 MPa之间，均值为1.93 MPa，均方差为0.594 MPa。上游折坡处的第一主应力峰值稍小，峰值范围在 0.63 MPa和1.71 MPa之间，均值为1.08 MPa，均方差为0.345 MPa。下游坝面的第一主应力峰值比下游面折坡处稍大，具体数据见表2。
总体而言，坝顶加速度和相对位移峰值的变异性稍低，变异系数分别为0.103和0.130，说明坝顶加速度和相对位移在随机波场影响下出现的变化较小。坝体特征部位第一主应力响应的变异性稍大，变异系数在0.257和0.319之间，说明坝体特征部位的第一主应力峰值在随机波场影响下的变异性稍大于坝顶加速度和相对位移。
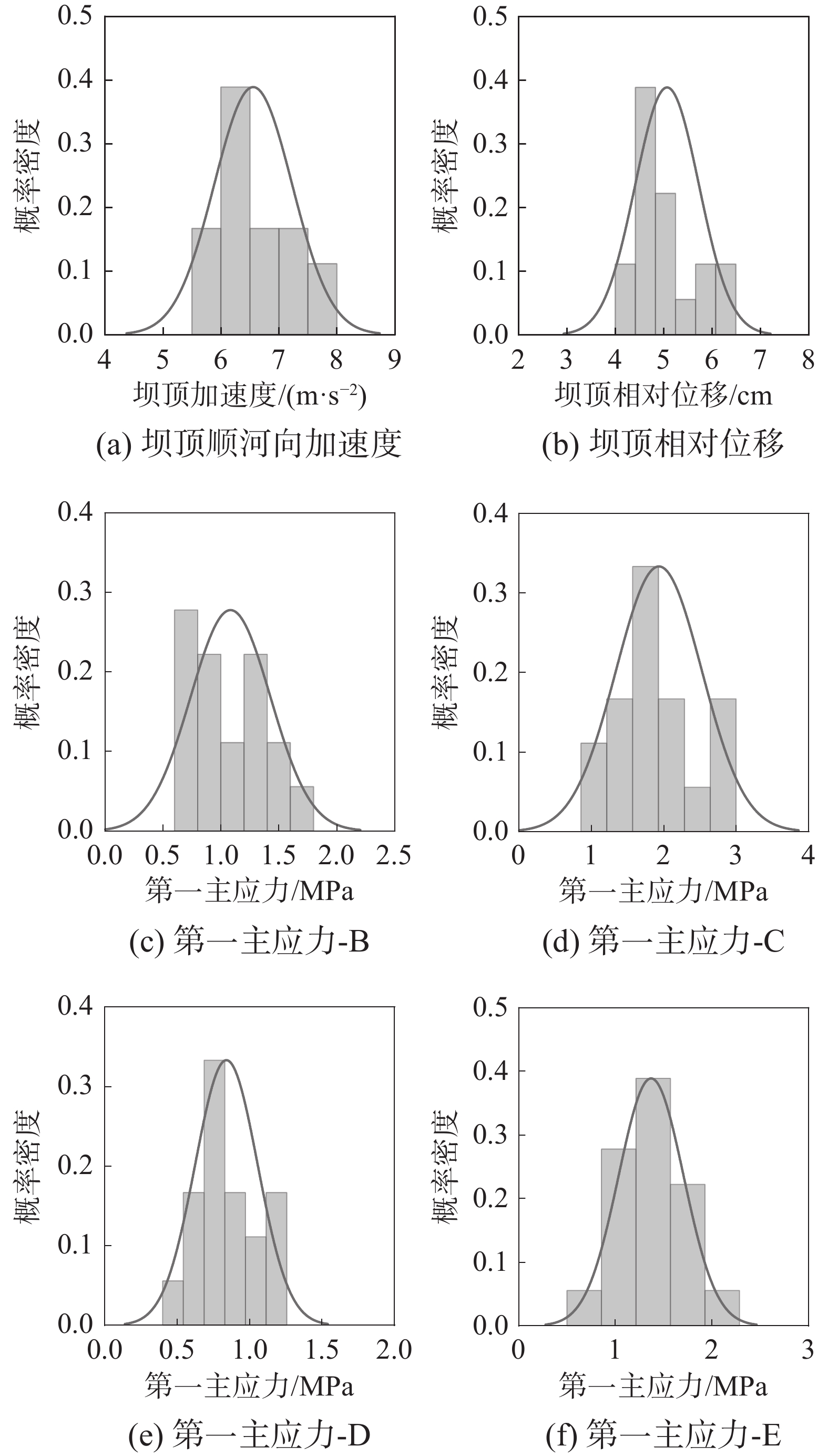
为显示特征部位峰值响应的分布特征，将坝顶加速度、坝顶相对位移和4个部位第一主应力的直方分布在图7显示，图7中分布曲线为由表2数据得到的正态分布区曲线。由图7可知，特征位置峰值响应大致服从正态分布。
3.4 特征部位响应时程与坝踵单元破坏分析
图8给出坝顶的加速度和相对位移、坝踵第一主应力的时程变化情况，包含峰值最大和峰值最小方案。
由图8可知，计算方案中结构响应时程形状存在显著差异，且峰值出现时间也不相同，这是由非一致波动输入能模拟不同地震波的复杂叠加情况引起。图8中显示的最大峰值和最小峰值方案中，顺河向加速度时程峰值出现时间分别为5.13 s和5.42 s，坝顶顺河向相对位移时程的峰值出现时间分别为7.15 s和8.34 s，坝踵第一主应力峰值的出现时间分别为5.53 s和6.98 s。
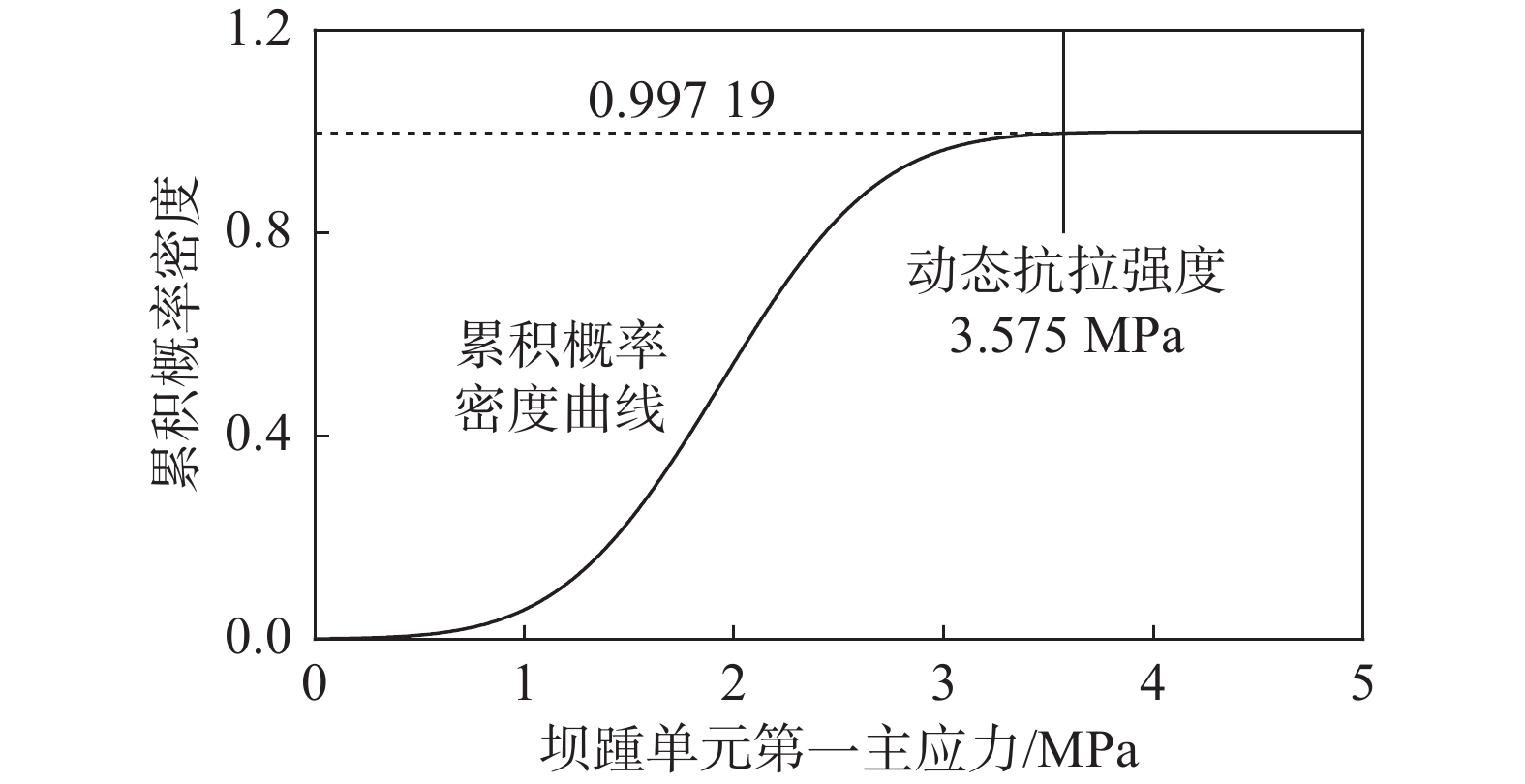
以随机地震响应分析结果考察坝踵单元第一主应力峰值超过抗拉强度的概率。由前文结果可知，坝踵第一主应力响应大致服从正态分布，以正态分布和18个算例结果计算累积概率密度，在图9显示。参考已有文献[39]，向家坝工程坝踵部位混凝土的静态抗拉强度为2.75 MPa，动态抗拉强度按1.3倍计算为3.575 MPa。依据考虑复杂波场影响得到的重力坝随机地震响应分析结果，坝踵单元第一主应力峰值小于动态抗拉强度的累积概率密度为0.99719。由此可知，坝踵单元第一主应力峰值结果超过抗拉强度的概率，即坝踵单元受拉破坏的概率为0.281%。
4 结论
针对重力坝随机地震响应分析尚未有效考虑复杂波场的影响，本文提出获得场址入射波信息的随机波场模型，并结合非一致波动输入对向家坝工程非溢流坝段的随机地震响应开展分析，得出以下结论。
(1) 以重力坝场地谱为目标，随机波场模型可在确保参考点水平向运动反应谱与场地谱一致前提下，有效获取匹配重力坝场址的复杂入射波场信息。以复杂入射波场信息构建的非一致波动输入能够精确模拟地面运动，选定算例中得到的参考点运动加速度、速度和位移的最大误差分别为3.75%、1.59%和0.02%，证实非一致波动输入可用于重力坝结构的随机地震响应分析。
(2) 复杂波场影响下，选定坝段的顺河向加速度的峰值均值随坝高增加逐渐增大，在坝踵峰值均值为1.58 m/s2，在坝顶峰值均值为6.56 m/s2，坝顶的加速度峰值均值相对水平向设计地震动峰值放大约3.0。该坝段第一主应力峰值表现为受拉区域主要分布在上游折坡及以上部位、坝踵、下游折坡及以下部位，三个区域第一主应力峰值均值在上游折坡处为1.08 MPa，在坝踵为1.93 MPa，在下游坝面为1.37 MPa。该坝段的坝头偏小，鞭梢效应并不显著，因此在下游折坡处的第一主应力峰值均值较小，为0.84 MPa。
(3) 该坝段的坝顶加速度和相对位移峰值在随机波场影响下的变异性较低，变异系数分别为0.103和0.130。坝体特征部位拉应力响应在随机波场影响下变异性稍大，变异系数在0.245和0.319之间。受复杂波场间叠加效果的影响，坝体特征部位响应除峰值不同外，也存在显著的峰值时刻和时程形状差异。本文算例中，考虑复杂波场影响下重力坝坝踵第一主应力峰值区间为1.02~2.95 MPa，依据正态分布得到的坝踵单元受拉破坏概率为0.281%，说明该坝段在设计峰值地震动对应的复杂波场影响下具备较强的抗震安全性。
-
![]()
图 2 某算例参考点两向地面运动
Figure 2. Two-component ground accelerations at reference point in one case
![]()
图 3 场地谱与参考点水平向加速度反应谱
Figure 3. Site spectrum and response spectrums of horizontal acceleration at reference point
![]()
图 4 非一致波动输入参考点地面运动
Figure 4. Ground motion at the reference point by non-uniform wave input method
![]()
图 5 向家坝非溢流坝段有限元模型
Figure 5. Finite element model of non-overflow monolith in Xiangjiaba gravity dam
表 1 坝体和地基材料参数
Table 1 Parameters of dam concrete and foundation
材料区域 弹性模量/GPa 泊松比 密度/(kg·m−3) 坝体 I区 42.00 0.167 2550 II区 26.25 0.167 2550 III区 38.25 0.167 2550 IV区 42.00 0.167 2550 地基 12.00 0.250 2600 
下载: 导出CSV
表 2 重力坝特征位置的随机地震响应
Table 2 Random response of gravity dam at chosen poisitons
响应量 位置 最大值 最小值 均值 均方差 变异系数 水平向加速度
峰值/(m·s−2)A 7.94 5.57 6.56 0.672 0.103 相对位移峰值/cm A 6.40 4.33 5.07 0.660 0.130 第一主应力
峰值/MPaB 1.71 0.63 1.08 0.345 0.319 C 2.95 1.02 1.93 0.594 0.307 D 1.21 0.48 0.84 0.216 0.257 E 1.94 0.86 1.37 0.336 0.245
下载: 导出CSV
-
[1] ZERVA A. Spatial variation of seismic ground motions: Modeling and engineering applications [M]. Boca Raton: CRC Press, 2009: 9 − 64.
[2] 何卫平, 熊堃, 卢晓春. 确定性地震动空间差异对重力坝地震响应影响研究[J]. 水利学报, 2019, 50(8): 913 − 924. HE Weiping, XIONG Kun, LU Xiaochun. Influence of deterministic spatial variation of motions on seismic response of gravity dam [J]. Journal of Hydraulic Engineering, 2019, 50(8): 913 − 924. (in Chinese)
[3] CLOUGH R W, PENZIEN J. Dynamics of structures [M]. 3nd ed. Berkeley: Computers & Structures, Inc., 1996: 15 − 32.
[4] JOYNER W B, CHEN A T F. Calculation of nonlinear ground response in earthquakes [J]. Bulletin of the Seismological Society of America, 1975, 65(5): 1315 − 1336.
[5] 廖振鹏. 工程波动理论导论[M]. 2版. 北京: 科学出版社, 2002: 136 − 285. LIAO Zhenpeng. Introduction to wave motion theories in engineering [M]. 2nd ed. Beijing: Science Press, 2002: 136 − 285. (in Chinese)
[6] 刘晶波, 吕彦东. 结构-地基动力相互作用问题分析的一种直接方法[J]. 土木工程学报, 1998, 31(3): 55 − 64. LIU Jingbo, LYU Yandong. A direct method for analysis of dynamic soil-structure interaction [J]. China Civil Engineering Journal, 1998, 31(3): 55 − 64. (in Chinese)
[7] 杜修力. 工程波动理论与方法[M]. 北京: 科学出版社, 2009: 367 − 431. DU Xiuli. Theories and methods of wave motion for engineering [M]. Beijing: Science Press, 2009: 367 − 431. (in Chinese)
[8] 孔宪京, 屈永倩, 邹德高, 等. 强震作用下面板堆石坝跨尺度面板开裂演化分析[J]. 岩土工程学报, 2020, 42(6): 989 − 996. doi: 10.11779/CJGE202006001 KONG Xianjing, QU Yongqian, ZOU Degao, et al. Cross-scale crack evolution analysis for face slab in concrete faced rockfill dams under strong earthquake [J]. Chinese Journal of Geotechnical Engineering, 2020, 42(6): 989 − 996. (in Chinese) doi: 10.11779/CJGE202006001
[9] 赵密. 近场波动有限元模拟的应力型时域人工边界条件及其应用[D]. 北京: 北京工业大学, 2009. ZHAO Mi. Stress-type time domain artificial boundary condition for finite-element simulation of near-field wave motion and its engineering application [D]. Beijing: Beijing University of Technology, 2009. (in Chinese)
[10] TASAKETH I, CEN W J, LIU B, et al. Nonlinear seismic response of SV wave incident angle and direction to concrete gravity dam [J]. International Journal of Civil Engineering, 2022, 20(12): 1479 − 1494. doi: 10.1007/s40999-022-00756-7
[11] XU S T, XU Q, CHEN J Y, et al. Seismic performance analysis of gravity dam system under arbitrary oblique incidence of near-fault SV ground motions [J]. International Journal of Geomechanics, 2022, 22(12): 04022240. doi: 10.1061/(ASCE)GM.1943-5622.0002599
[12] 康昊, 郭子雄, 刘洋, 等. 基于CNN的考虑地震波时频特征影响选波方法研究[J]. 工程力学, 2023, 40: 1 − 13, doi: 10.6052/j.issn.1000-4750.2023.05.0348. KANG Hao, GUO Zixiong, LIU Yang, et al. Research on ground motion selection method considering the impact of time and frequency characteristics of ground motions based on CNN [J]. Engineering Mechanics, 2023, 40: 1 − 13, doi: 10.6052/j.issn.1000-4750.2023.05.0348. (in Chinese)
[13] 张锐, 王东升, 孙治国, 等. 以结构反应均值估计为目标的时程分析输入地震波选择研究[J]. 工程力学, 2022, 39(12): 74 − 86. doi: 10.6052/j.issn.1000-4750.2021.07.0521 ZHANG Rui, WANG Dongsheng, SUN Zhiguo, et al. Selection and scaling of ground motions in time-history analysis for estimates of mean structural responses [J]. Engineering Mechanics, 2022, 39(12): 74 − 86. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.07.0521
[14] 王晓磊, 赵紫旭, 阎卫东, 等. 基于中国场地向量型条件谱的水平和竖向地震动联合选取研究[J]. 工程力学, 2023, 41: 1 − 17, doi: 10.6052/j.issn.1000-4750.2023.06.0446. WANG Xiaolei, ZHAO Zixu, YAN Weidong, et al. Study on joint selection of horizontal and vertical ground motions based on vector conditional spectra of Chinese sites [J]. Engineering Mechanics, 2023, 41: 1 − 17, doi: 10.6052/j.issn.1000-4750.2023.06.0446. (in Chinese)
[15] 俞瑞芳, 张翠然, 张冬锋, 等. 基于近场发震构造最大可信地震的坝址设计参数综合评价[J]. 土木工程学报, 2022, 55(3): 117 − 128. YU Ruifang, ZHANG Cuiran, ZHANG Dongfeng, et al. Study on design parameters for dam site based on maximum credible earthquake of near-field seismogenic structure [J]. China Civil Engineering Journal, 2022, 55(3): 117 − 128. (in Chinese)
[16] WANG G H, WANG Y X, LU W B, et al. Damage demand assessment of mainshock-damaged concrete gravity dams subjected to aftershocks [J]. Soil Dynamics and Earthquake Engineering, 2017, 98: 141 − 154. doi: 10.1016/j.soildyn.2017.03.034
[17] GORAI S, MAITY D. Seismic response of concrete gravity dams under near field and far field ground motions [J]. Engineering Structures, 2019, 196: 109292. doi: 10.1016/j.engstruct.2019.109292
[18] 何蕴龙, 陆述远. 重力坝随机地震动力分析方法研究[J]. 水利学报, 2000(1): 35 − 41. doi: 10.3321/j.issn:0559-9350.2000.01.007 HE Yunlong, LU Shuyuan. Study on random seismic analysis method for gravity dam [J]. Journal Of Hydraulic Engineering, 2000(1): 35 − 41. (in Chinese) doi: 10.3321/j.issn:0559-9350.2000.01.007
[19] 张社荣, 王超, 孙博. 基于性能的重力坝随机地震反应概率特征[J]. 天津大学学报(自然科学与工程技术版), 2013, 46(7): 603 − 610. ZHANG Sherong, WANG Chao, SUN Bo. Probabilistic characteristics of the performance-based seismic response of concrete gravity dams [J]. Journal of Tianjin University (Science and Technology), 2013, 46(7): 603 − 610. (in Chinese)
[20] LUPOI A, CALLARI C. A probabilistic method for the seismic assessment of existing concrete gravity dams [J]. Structure and Infrastructure Engineering, 2012, 8(10): 986 − 998.
[21] 刘章军, 曾波, 周宜红, 等. 地震动过程的概率模型及在重力坝抗震可靠度分析中的应用[J]. 水利学报, 2014, 45(9): 1066 − 1074. LIU Zhangjun, ZENG Bo, ZHOU Yihong, et al. Probabilistic model of ground motion processes and seismic dynamic reliability analysis of the gravity dam [J]. Journal of Hydraulic Engineering, 2014, 45(9): 1066 − 1074. (in Chinese)
[22] DE ARAÚJO J, AWRUCH A M. Probabilistic finite element analysis of concrete gravity dams [J]. Advances in Engineering Software, 1998, 29(2): 97 − 104. doi: 10.1016/S0965-9978(98)00052-0
[23] HUANG J J. Earthquake damage analysis of concrete gravity dams: Modeling and behavior under near-fault seismic excitations [J]. Journal of Earthquake Engineering, 2015, 19(7): 1037 − 1085. doi: 10.1080/13632469.2015.1027019
[24] 张季, 谭灿星, 叶国涛, 等. SV波超临界角斜入射时层状地基地震动输入在ABAQUS中的实现[J]. 工程力学, 2021, 38(4): 200 − 210. doi: 10.6052/j.issn.1000-4750.2020.06.0378 ZHANG Ji, TAN Canxing, YE Guotao, et al. Realization of ground motion input in ABAQUS for layered foundation under SV wave of oblique incidence over critical angle [J]. Engineering Mechanics, 2021, 38(4): 200 − 210. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.06.0378
[25] 章旭斌, 谢志南. 波动谱元模拟中透射边界稳定性分析[J]. 工程力学, 2022, 39(10): 26 − 35. doi: 10.6052/j.issn.1000-4750.2021.06.0428 ZHANG Xubin, XIE Zhinan. Stability analysis of transmitting boundary in wave spectral element simulation [J]. Engineering Mechanics, 2022, 39(10): 26 − 35. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.06.0428
[26] 李明超, 张佳文, 张梦溪, 等. 地震波斜入射下混凝土重力坝的塑性损伤响应分析[J]. 水利学报, 2019, 50(11): 1326 − 1338,1349. LI Mingchao, ZHANG Jiawen, ZHANG Mengxi, et al. Plastic damage response analysis of concrete gravity dam due to obliquely incident seismic waves [J]. Journal of Hydraulic Engineering, 2019, 50(11): 1326 − 1338,1349. (in Chinese)
[27] 余翔, 孔宪京, 邹德高, 等. 覆盖层上土石坝非线性动力响应分析的地震波动输入方法[J]. 岩土力学, 2018, 39(5): 1858 − 1866, 1876. YU Xiang, KONG Xianjing, ZOU Degao, et al. Seismic wave input method for nonlinear dynamic analysis of earth dam built on overburden [J]. Rock and Soil Mechanics, 2018, 39(5): 1858 − 1866, 1876. (in Chinese)
[28] HUANG J Q, ZHAO M, DU X L. Non-linear seismic responses of tunnels within normal fault ground under obliquely incident P waves [J]. Tunnelling and Underground Space Technology, 2017, 61: 26 − 39. doi: 10.1016/j.tust.2016.09.006
[29] 宝鑫, 刘晶波, 李述涛, 等. 土-结构相互作用对储液结构动力反应的影响研究[J]. 工程力学, 2021, 38(增刊1): 125 − 132. doi: 10.6052/j.issn.1000-4750.2020.06.S022 BAO Xin, LIU Jingbo, LI Shutao, et al. Influence analysis of soil-structure interaction on the dynamic response of storage tanks [J]. Engineering Mechanics, 2021, 38(Suppl 1): 125 − 132. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.06.S022
[30] 何卫平. 考虑波传播特点的地震动场及工程应用[D]. 武汉: 武汉大学, 2015. HE Weiping. Seismic motion field considering propagation character of wave and application in engineering [D]. Wuhan: Wuhan University, 2015. (in Chinese)
[31] 何卫平. 重大工程场址复杂入射波场信息的确定性评估方法[R]. 北京: 北京工业大学, 2021. HE Weiping. Deterministic assessment of site wave field in major project site [R]. Beijing: Beijing University of Technology, 2021. (in Chinese)
[32] 何卫平, 杜修力, 陈平, 等. 基于场址复杂入射波场的非一致波动输入模型[J]. 工程力学, 2023, 40: 1 − 10, doi: 10.6052/j.issn.1000-4750.2022.08.0688. HE Weiping, DU Xiuli, CHEN Ping, et al. A non-uniform wave input model based on complex incident site waves [J]. Engineering Mechanics, 2023, 40: 1 − 10, doi: 10.6052/j.issn.1000-4750.2022.08.0688. (in Chinese)
[33] HE W P, DU X L, YUE M K, et al. A random non-uniform wave input method based on complex incident site waves [J]. Computers & Structures, 2023, 288: 107145.
[34] 陈运泰. 多层弹性半空间中的地震波(一)[J]. 地球物理学报, 1974, 17(1): 20 − 43. CHEN Yuntai. Seismic waves in multilayered elastic half-space (I) [J]. Acta Geophysica Sinica, 1974, 17(1): 20 − 43. (in Chinese)
[35] POURSARTIP B, FATHI A, TASSOULAS J L. Large-scale simulation of seismic wave motion: A review [J]. Soil Dynamics and Earthquake Engineering, 2020, 129: 105909. doi: 10.1016/j.soildyn.2019.105909
[36] AKI K, RICHARDS P G. Quantitative seismology [M]. 2nd ed. Sausalito: University Science Books, 2002: 119 − 188.
[37] 万永革. 地震学导论[M]. 北京: 科学出版社, 2016: 83 − 113. WAN Yongge. Introduction to seismology [M]. Beijing: Science Press, 2016: 83 − 113. (in Chinese)
[38] 杜修力, 赵密, 王进廷. 近场波动模拟的人工应力边界条件[J]. 力学学报, 2006, 38(1): 49 − 56. doi: 10.3321/j.issn:0459-1879.2006.01.007 DU Xiuli, ZHAO Mi, WANG Jinting. A stress artificial boundary in FEA for near-field wave problem [J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(1): 49 − 56. (in Chinese) doi: 10.3321/j.issn:0459-1879.2006.01.007
[39] 王振. 基于参数非均质性的重力坝渗流-应力-损伤耦合分析[D]. 天津: 天津大学, 2018. WANG Zhen. Seepage-stress-damage coupling analysis of gravity dam based on parameter heterogeneity [D]. Tianjin University, 2018.
计量
- 文章访问数: 31
- HTML全文浏览量: 13
- PDF下载量: 9
