STUDY ON THE METHOD OF STRUCTURAL SEISMIC DAMAGE PREDICTION BASED ON KRIGING SURROGATE MODEL
-
摘要:
提出了针对泸定县某博物馆多层框架结构的基于Kriging模型的结构震害预估方法，并根据在2022年9月5日发生的泸定6.8级地震中该多层框架结构出现的震害，对提出的震害预估方法进行了验证。基于Kriging模型的结构震害预估方法具体流程方法如下：建立结构的有限元模型；选用能够代表结构所在场地特性的近断层地震动记录进行弹塑性时程分析；根据时程分析得到的基底剪力、位移数据训练Kriging模型，并得到结构的抗震能力曲线；根据时程分析输入的多元地震动参数和基底剪力、位移数据训练Kriging模型，并结合LASSO正则化方法和K-means聚类算法得到结构的抗震需求Kriging模型；基于抗震能力曲线定义结构的震害评价标准，根据抗震需求Kriging模型和潜在地震的地震动参数对结构进行震害预估。研究结果表明：当采用300个训练数据时，基于Kriging模型的震害预估方法能够满足工程需求，可以作为HAZUS法改进的参考；在数据有限的情况下，特征选择方法可以提高Kriging模型的准确性，但K-means聚类算法并不能有效的提高结果的准确性；训练数据获取成本较高是Kriging模型在结构抗震领域应用的限制因素。
Abstract:A structural damage prediction method based on the Kriging surrogate model was proposed for a multi-storey frame structure of a museum in Luding. The method proposed was validated upon the seismic damage of the multi-storey frame structure in the Luding Ms6.8 earthquake that occurred on September 5, 2022. The specific process and method of structural seismic damage prediction based on the Kriging surrogate model are as follows: Establishing a finite element model of the structure; Selecting near-fault seismic motion records that can represent the characteristics of the site where the structure is located for elastic-plastic time history analysis; Training the Kriging surrogate model by the base shear and by displacement data obtained from time-history analysis to obtain the seismic capacity curve of the structure; Combining with LASSO regularization method and K-means clustering algorithm, and training the Kriging surrogate model by the input multiple seismic parameters, by the base shear and, by the displacement data from time-history analysis to obtain the seismic demand Kriging surrogate model of the structure; According to the seismic capacity curve, defining the seismic damage evaluation criteria for the structure, and estimating the seismic damage of the structure based on the seismic demand Kriging surrogate model and, on potential seismic motion parameters. The research results indicate that: When using 300 sets of training data, the earthquake damage prediction method based on the Kriging surrogate model can meet engineering requirements and serve as a reference for improving the HAZUS method; In the case of limited data, feature selection methods can improve the accuracy of the Kriging surrogate model, but the K-means clustering algorithm cannot effectively improve the accuracy of the results; The high cost of obtaining training data is a limiting factor for the application of Kriging surrogate models in the field of structural seismic analysis.
-
我国是世界大陆地震活动最强烈的国家之一，同时地震对于我国经济和社会发展有重大影响[1 − 3]。在地震发生前，对结构可能出现的震害进行预估，并制定相应的措施可以进一步保证震后救援行动的成功。美国联邦应急管理署(FEMA)开发的HAZUS软件，用于灾后社会经济损失估计、灾前紧急情况预警以及用于灾害恢复的多灾害损失估计[4 − 5]。HAZUS软件采用了基于能力谱法的地震损失预估方法(以下简称HAZUS法)，HAZUS法的震害预估流程为[5 − 7]：1)根据结构的类型、建成时间和设防规范将结构分类；2)对于每一类型的结构分别建立能力曲线和概率性抗震需求曲线；3)根据能力曲线和需求曲线的交点得到某一类型结构的性能点，再根据性能先来判断结构的破坏情况。然而，HAZUS法属于半解析半数值法，计算中需要对问题进行一定的简化，结果导致了HAZUS法存在的以下缺陷：1)能力曲线和需求曲线均是代表某一类型结构的平均曲线，针对性不足；2)能力曲线和需求曲线均根据单一参数建立，对地震动的复杂性考虑不足；3)需求曲线是对时程分析结果进行回归得到的，而在时程分析中，地震动选取存在随机性，最终的需求曲线不能完全客观的反映结构的抗震需求；4)能力曲线是通过非线性静力分析得到的，无法考虑结构的动力特性和地震动的特点，造成了结果的不准确[8]。
相比HAZUS法中所采用的半解析法，数值方法具有前置条件少，精度高，理论简单等优点。近年来随着代理模型的发展，结构数值模拟的计算量得到了有效降低，为基于数值方法的震害预估奠定了基础。Kriging模型作为一种代理模型，能够较好的处理计算效率和准确性之间的权衡问题，在结构优化、风险预估、敏感性分析等计算量较大的问题上得到了广泛应用。BERNARDINI等[9]提出了基于Kriging模型的改进算法对高层结构和大跨度桥梁的气动外形进行了优化；GIDARIS等[10]，采用Kriging模型和K-means聚类算法建立了一种有效的地震预估风险计算流程，提供了结构响应与地震动参数之间的近似关系；JIA等[11]结合特征选择方法，采用Kriging模型对沿海地区的飓风、风暴风险进行了预估；LI等[12]采用主成分分析方法和Kriging模型，提出了一种高效的敏感性分析方法，并将其应用在了复杂系统敏感性分析问题上，取得了很好的效果；KYPRIOTI等[13]将Kriging模型应用于地震风险评估中，很好的解决了由于地震的随机性所产生的问题。此外，Kriging模型具备良好的稳定性，在航空航天领域中的复杂问题上也有着广泛的应用[14 − 16]。Kriging模型能够很好地解决非线性较高和存在局部响应突变的问题，适用于结构的抗震分析。Kriging模型可以实现地震动的多元参数输入，从根本上消除了HAZUS法采用单参数进行评估所带来的偏差；同时，由于能够考虑结构的动力特性，Kriging模型可以更准确的分析结构的抗震能力，但是对于训练数据量不足的情况，需要采用一定的方法提高Kriging模型的训练效率。
综上，本文提出一种基于Kriging模型的震害预估方法，采用LASSO正则化方法作为特征选择方法，并结合K-means聚类算法，提高Kriging模型的训练效率和准确性，针对位于泸定县磨西镇的某博物馆多层框架，采用弹塑性时程分析结果训练Kriging模型，对该结构震害进行预估，并根据该结构在地震中的实际破坏情况，对基于Kriging模型的震害预估方法进行验证。
1 Kriging模型与加强方法
1.1 Kriging模型
本文提出的震害预估方法以Kriging模型为基础，采用地震动参数与结构响应数据对Kriging模型进行训练，通过训练后的Kriging模型分别得到结构的抗震能力和抗震需求，从而对结构在潜在地震作用下产生的震害进行预估。Kriging模型是一个参数化的“输入-输出”系统，可以取代有限元模型，实现抗震需求分析中地震动的参数化输入。对于系统y(X)=g(X)，Kriging模型的数学表达式可写为[16]：
g(X)=fT(X)β+z(X) (1) 式中：y(X)为输出参数；g(X)为待训练的Kriging模型；fT(X)=[f1(X),f2(X),⋯,fp(X)]为输入变量X的基函数，p为基函数的个数；β=[β1,β2,⋯,βp]T为待定参数，根据训练集进行估计；z(X)为Kriging模型局部偏差的随机过程，期望为0，方差为σ2k。
式(1)中z(X)的协方差可写为：
{{\mathrm{cov}}} \left[ {{\textit{z}}\left( {{{\boldsymbol{x}}_v}} \right),{\textit{z}}\left( {{{\boldsymbol{x}}_w}} \right)} \right] = \sigma _k^2\left[ {{R}\left( {\varTheta ,{{\boldsymbol{x}}_v},{{\boldsymbol{x}}_w}} \right)} \right] (2) 式中： R\left( {\varTheta ,{{\boldsymbol{x}}_v},{{\boldsymbol{x}}_w}} \right) 为样本点 {{\boldsymbol{x}}_v}, 和 {{\boldsymbol{x}}_w} 的相关函数； v, w=1, 2, …, m，m为训练集的样本个数； \varTheta 为模型的超参数， \varTheta = {\left[ {{\theta _1}, \cdots ,{\theta _i}, \cdots ,{\theta _l}} \right]^{\rm T}} ，l是输入参数X特征数量。
本文选取Matern型作为相关函数的形式，则 R\left( {\varTheta ,{{\boldsymbol{x}}_v},{{\boldsymbol{x}}_w}} \right) 可表示为：
\begin{split} & R\left( {\varTheta ,{x_v},{x_w}} \right) = \\& \frac{1}{{\varGamma (v){2^{v - 1}}}}{\left( {\frac{{\sqrt {2v} }}{\theta }\parallel {x_v} - {x_w}\parallel } \right)^v}{K_v}\left( {\frac{{\sqrt {2v} }}{\theta }\parallel {x_v} - {x_w}\parallel } \right) \end{split} (3) 式中： \parallel {{\boldsymbol{x}}_v} - {{\boldsymbol{x}}_w}\parallel 为欧几里得距离； {K}_{v}(\cdot ) 为修正Bessel函数； \varGamma (\cdot ) 为Gamma函数；参数 v 控制相关函数的平滑度，本文取值为1.5；参数 \varTheta 是特征长度尺度参数，特征长度尺度越小代表样本间的相关性越高。为提高Kriging模型的鲁棒性，可将 \varTheta 作为模型参数进行优化[13]。
式(1)中的待定参数 \beta 的估计值 \hat \beta 可表示为：
\hat \beta = {( {{F^{\rm T}}{R^{ - 1}}F} )^{ - 1}}F{R^{ - 1}}Y (4) 式中：R为对应于m个训练样本的相关函数矩阵；F为由p个基函数在全部m个训练样本点处的值组成的 m \times p 阶矩阵；Y为全部训练集样本输出值组成的列向量。
{\textit{z}}(X) 的方差 \sigma _k^2 的估计值 \hat \sigma _k^2 ，可根据最小二乘理论，按下式进行估计：
\hat \sigma _k^2 = \frac{1}{m}(Y - F\hat \beta ){R^{ - 1}}(Y - F\hat \beta ) (5) 本文通过极大似然估计得到超参数 \varTheta = [ {\theta _1}, \cdots , {\theta _i}, \cdots ,{\theta _l} ]^{\rm T} ，计算公式为：
\underset{\varTheta > 0}{\mathrm{min}}(Y-F\hat{\beta }){R}^{-1}(Y-F\hat{\beta })+\mathrm{det}(R) (6) 式中， \det {\text{(}} \cdot {\text{)}} 代表矩阵行列式。
Kriging模型的训练过程即是对超参数 \varTheta 的求解过程，由于 \varTheta 没有解析解，需要采用无梯度算法进行计算，如拟牛顿法、等梯度算法或遗传算法等[13]，其具体训练方法应根据数据特点进行选择。Kriging模型训练完成后，对于未知样本 x' ， {\textit{z}}(x') 可根据下式计算：
{\textit{z}}\left( {x'} \right) = {r^{\rm T}}\left( {x'} \right){R^{ - 1}}(Y - F\hat \beta ) (7) 式中， {r^{\rm T}}\left( {x'} \right) 为单个样本与训练样本的相关性， {r^{\rm T}}\left( {x'} \right) = {\left[ {R\left( {x',{x_1}} \right),R\left( {x',{x_2}} \right), \cdots ,R\left( {x',{x_m}} \right)} \right]^{\rm T}} 。
根据式(1)和式(7)，可得Kriging模型对未知样本 x' 的输出结果的最优无偏估计 \hat g\left( {x'} \right) ， \hat g\left( {x'} \right) 可写为：
\hat g\left( {x'} \right) = {f^{\rm T}}\left( {x'} \right)\hat \beta + {r^{\rm T}}\left( {x'} \right){R^{ - 1}}(Y - F\hat \beta ) (8) 对于训练后的Kriging模型，采用确定系数R2作为其模拟结果准确性的评价指标，当R2越接近1时，表示Kriging模型结果参考价值越高，确定系数R2的表达式为：
{R}^{2}=1-\frac{\displaystyle\sum _{k=1}^{m}{[\hat{g}\left({x}_{k}\right)-\overline{y}]}^{2}}{\displaystyle\sum _{k=1}^{m}{[y\left({x}_{k}\right)-\overline{y}]}^{2}} (9) 式中： y\left( {{x_k}} \right) 为样本 {x_k} 对应的实际输出结果； \overline y 为实际输出结果的平均值。
1.2 LASSO正则化方法
Kriging模型的准确性会受到输入参数数量的影响，因此需要对输入的地震动参数进行筛选，确保筛选后的地震动参数能够很好的反映地震动的特性，同时也能够准确模拟结构的地震响应。根据已有研究[17]，本文选用LASSO(least absolute shrinkage and selection operator)正则化方法对输入地震动参数进行筛选。LASSO正则化方法通过最小化数据拟合误差的平方和正则化项的和，实现数据的特征选择。本文以结构的基底剪力和最大层间位移作为因变量，地震动参数作为自变量，采用LASSO正则化方法对地震动参数进行筛选。LASSO正则化方法的具体算法通过公式可以表示为[17]：
\gamma = \mathop {{\mathrm{argmin}}}\limits_\gamma [ {{{( {| {C - {\gamma ^{\text{T}}}x} |} )}^2} + \lambda {W^{\text{T}}}\gamma } ] (10) 式中： \gamma 为回归系数向量， \gamma = {\left[ {{\gamma _1},{\gamma _2}, \cdots ,{\gamma _n}} \right]^{\text{T}}} ；C为结构基底剪力或最大层间位移；x为地震动参数的向量， x = {\left[ {{x_1},{x_2}, \cdots ,{x_n}} \right]^{\text{T}}} ； {W^{\text{T}}}\gamma 为惩罚函数； {W^{\text{T}}} 是各项数值为±1的向量，每一项与 \gamma 向量中对应项同号； \lambda 为正则化系数，用于控制回归系数压缩的程度。
\gamma 向量中的各项是地震动参数重要性的量化指标：对应的 \gamma 为正值，说明该地震动参数与结构响应正相关，反之为负相关， \gamma 的绝对值越大表明该地震动参数对结构响应的影响越大。
1.3 K-means聚类算法
本文采用K-means聚类算法提高Kriging模型的训练效率。作为应用最为广泛的聚类算法之一，K-means聚类算法具有简单、高效的优点。对于一个具有s个特征，d维数据点的数据集： H = \left\{ {{h_1},{h_2},{h_3}, \cdots ,{h_i}, \cdots ,{h_s}} \right\} ，其中 {h_i} \in {R^d} ，K-means聚类算法是将数据集H划分为K类，重新划分后的数据集 H = \left\{ {{C_k},k = 1,2, \cdots ,K} \right\} 。每一类数据集 {C_k} 具有一个聚类中心 {\mu _k} ，聚类中心 {\mu _k} 为每一类数据集 {C_k} 各数据点的平均值，根据欧几里得距离计算该类数据集各点到聚类中心 {\mu _k} 的距离平方和可根据下式计算[18]：
J\left({C}_{k}\right)=\sum _{{h}_{i}\in {C}_{k}}{\left|{h}_{i}-{\mu }_{k}\right|}^{2} (11) 聚类的目标是使得各类数据集的距离平方和 J(H)=\displaystyle\sum _{k=1}^{K}J\cdot \left({C}_{k}\right) 最小，因为 J(H) 会随着簇数K的增加而减小，而K值过大会导致聚类之间差异很小，反之，则会导致聚类之间差异很大。因此实施K-means聚类算法时，应找出最优的簇数K后，再通过求解 J(H) 的最小值来建立数据集 {C_k} 。
本文采用K-means聚类算法对原始数据进行分类处理，以提高训练后Kriging模型的准确性。具体流程如下：1)采用K-means聚类算法将所有数据分类；2)计算预测数据距离各聚类中心的距离，选择距离最近的簇作为训练数据；3)将训练数据按比例划分为训练集和测试集，对Kriging模型进行训练。
2 震害预估方法的建立
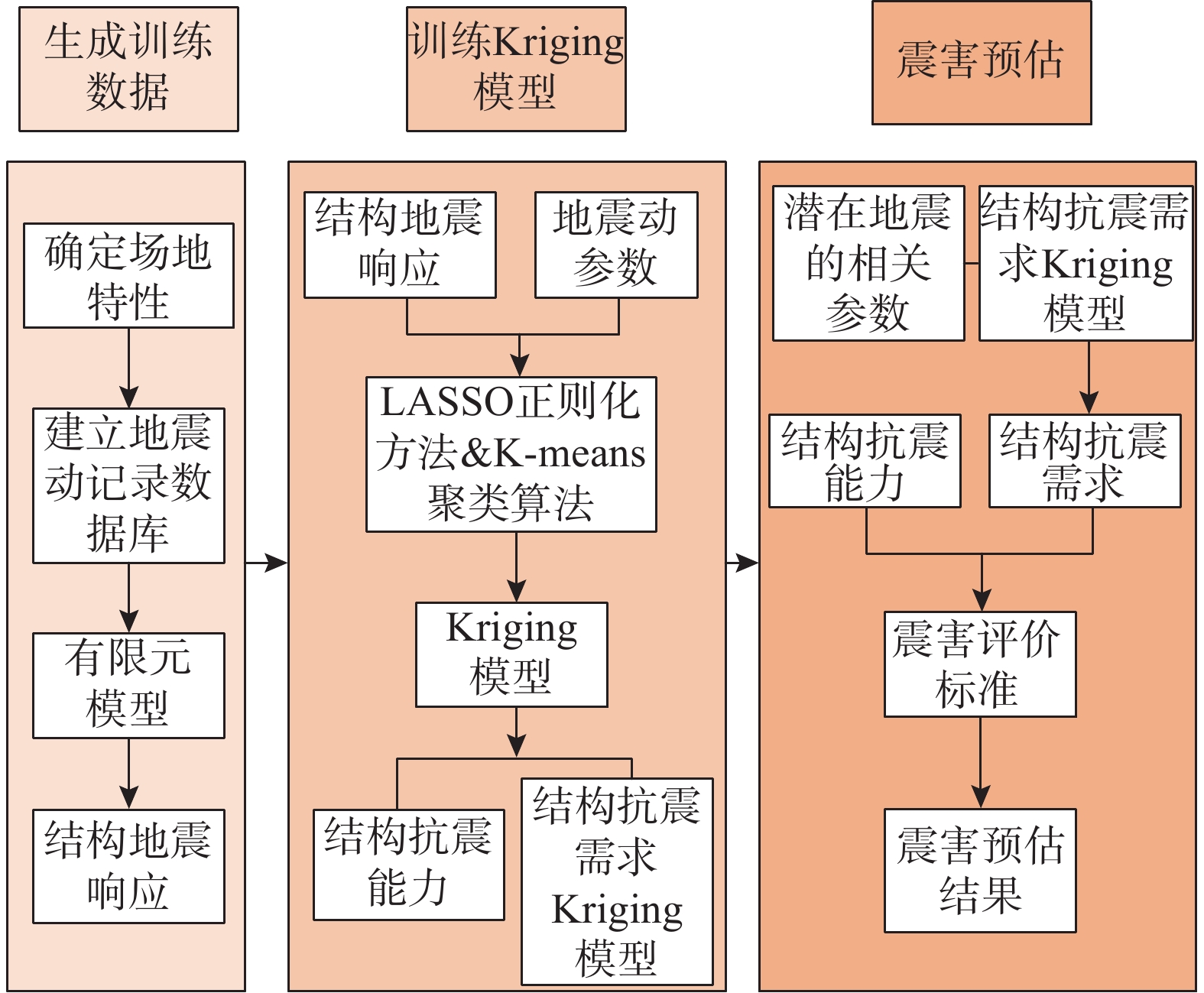
本文在能力谱法的基础上，建立针对指定结构的基于Kriging模型的震害预估方法，具体流程方法如下：1)建立结构的有限元模型；2)选用能够代表结构所在场地特性的地震动记录进行弹塑性时程分析；3)根据时程分析得到的基底剪力、位移数据训练Kriging模型，并得到结构的抗震能力曲线；4)根据时程分析输入的地震动参数和基底剪力、位移数据训练Kriging模型，得到结构的抗震需求Kriging模型；5)定义结构的震害评价标准，根据抗震需求Kriging模型和潜在地震的地震动参数对该结构进行震害预估。基于Kriging模型的震害预估方法的流程见图1。
![]()
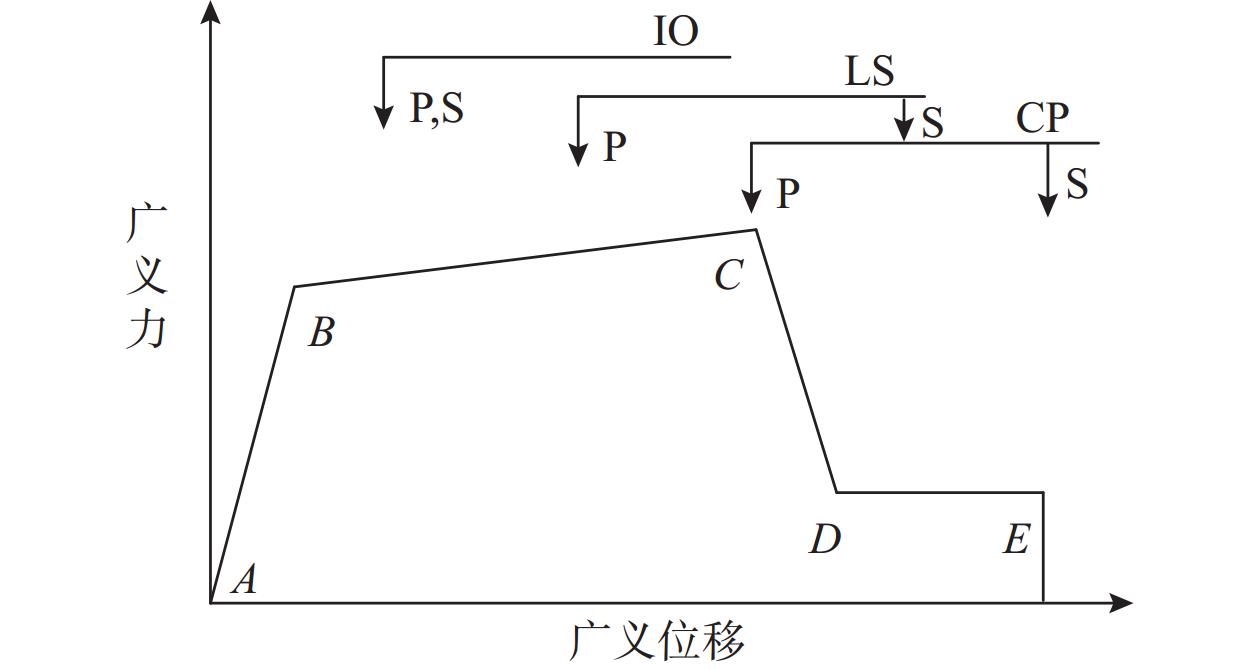
图 1 基于Kriging模型的震害预估流程图Figure 1. Flow chart of seismic damage prediction based on Kriging surrogate modelFEMA356[2]将结构分为主要结构(Primary, P)和次要结构(Secondary, S)两种类型，根据变形将结构的地震性能划分为OP (Operational)、IO (Immediate Occupancy)、LS (Life Safety)、CP (Collapse Prevention)四个等级，在本文中对应四个震害等级。其中，OP代表结构几乎没有损伤；IO代表结构处于安全状态，仅需要微小的维修；LS代表结构保持着一定的承载力，有害的非结构破坏在可控的范围内；CP代表结构虽然能够直立，但已经达到临界状态，除了人的生命，任何其它损失都是可能出现的[19]。本文参考FEMA356中的能力曲线，根据结构的刚度和变形建立震害分级标准。FEMA356中结构典型的抗震能力曲线见图2。
![]()
图 2 FEMA356抗震能力曲线示意[17]Figure 2. Schematic diagram of seismic capacity curve in FEMA356本文将结构整体刚度下降至初始刚度90%时，所对应的最大层间位移角定义为结构的屈服层间位移角[20]；将结构整体刚度下降至初始刚度70%时，所对应的最大层间位移角定义为结构的弹塑性层间位移角[20]；将结构整体刚度下降至初始刚度20%时，所对应的最大层间位移角定义为结构的极限层间位移角[20]；将结构所能达到的最大层间位移角限值定义为结构的临界位移角，当最大层间位移角超出此限值，结构将出现垮塌。根据所定义的三个最大层间位移角限值，可将结构的能力曲线分为五个区段：1)初始状态—屈服状态，对应的震害等级为“无损伤”(OP)；2)屈服状态—弹塑性状态，对应的震害等级为“轻度损伤”(IO)；3)弹塑性状态—极限状态，对应的震害等级为“中度损伤”(LS)；4)极限状态—临界状态，对应的震害等级为“严重损伤”(CP)；5)超过临界状态后结构出现局部或整体垮塌。
相比HAUZS法中采用Push-over分析得到的抗震能力曲线的做法，基于Kriging模型的抗震能力曲线能够反映结构在动力作用下的抗震能力，更接近结构实际的抗震能力。此外，抗震需求 Kriging模型考虑了结构的多自由度振动和地震动多元参数的影响，准确性同样高于HAUZS法中概率性的抗震需求曲线。相比直接采用有限元分析，基于Kriging模型的震害预估方法可以实现地震动参数化输入，在地震发生前，可以通过对该地区可能出现的地震的重要地震动参数进行预测，进而实现震害预估，不需要依赖地震动记录；同时基于Kriging模型的震害预估方法的计算效率更高，也可以用于震后震害的快速评估。
3 算例
3.1 有限元模型
位于泸定县摩西台地的某博物馆在 2022年9月5日发生的泸定6.8级地震中遭到严重破坏[21]，本文选用该博物馆中震害最具代表性的框架W2进行分析，并对提出的震害预估方法进行验证，博物馆详细信息见文献[21]。框架W2为二层框架结构，首层、二层高分别为4.8 m，4.2 m，典型柱网跨度为7.8 m；框架W2平面布置呈“L”形，短边的长宽比超过规范规定的限值，属于平面布置不规则结构[21]。框架W2在梁端设置了 “仿雀替”，“仿雀替”增大了梁端抗弯承载力，不利于梁柱节点在地震中实现“梁铰”机制，也削弱了结构的变形能力。 “仿雀替”构造及详细尺寸见文献[21]。
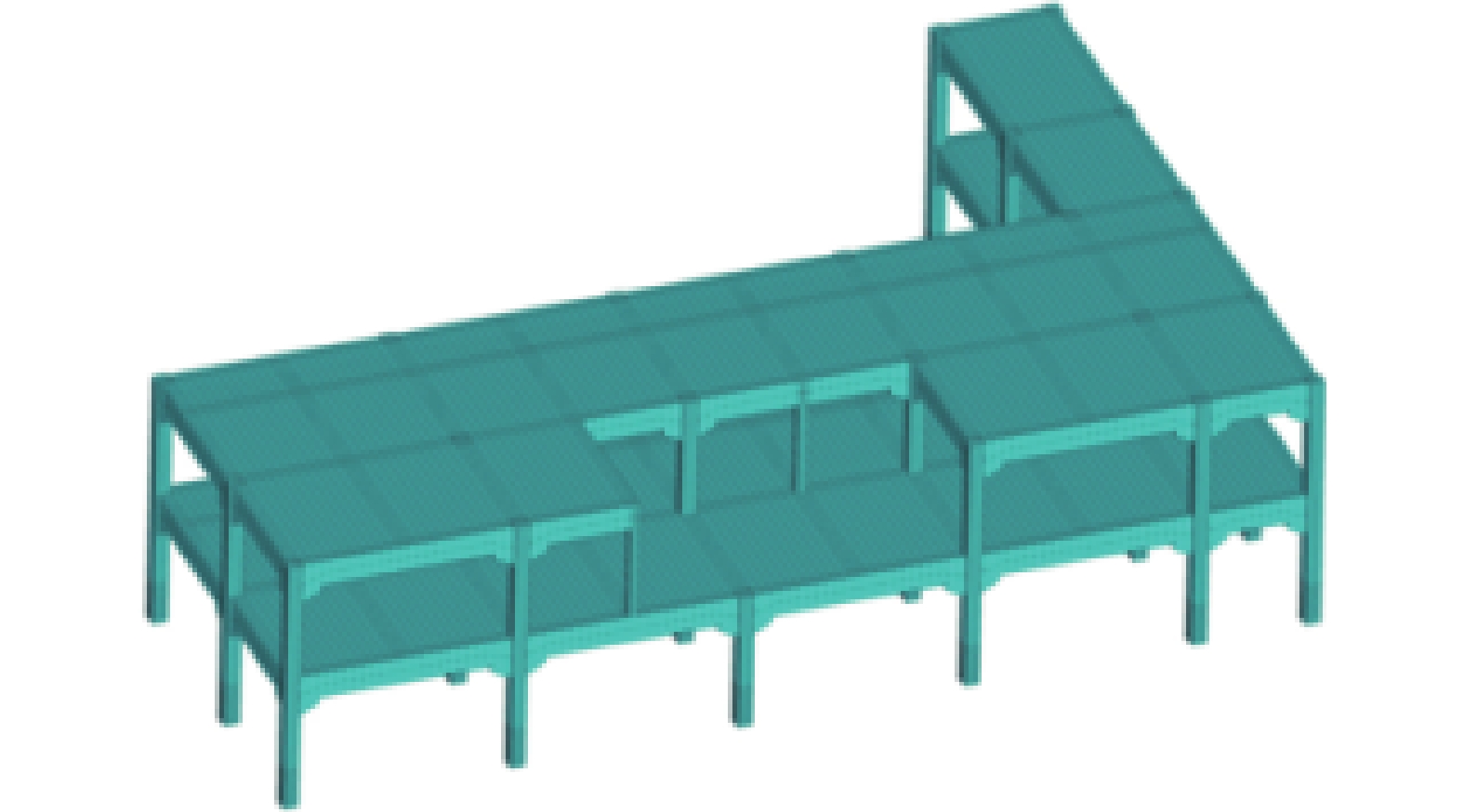
采用通用有限元软件ANSYS对框架W2进行精细化建模，有限元模型的参数设定见文献[21]，框架W2的有限元模型见图3。该有限元模型较准确的模拟了泸定地震中框架W2出现的震害[21]，本文中将其作为高保真度模型生成Kriging模型的训练数据。弹塑性时程分析中，地震动记录从南北、东西和竖直三个方向采用一致激励输入；根据泸定6.8级地震的实际情况，输入方向与框架W2主轴的夹角为47°。文中的弹塑性时程分析在国家超级计算天津中心的“天河一号”上完成。
3.2 地震动与地震动参数
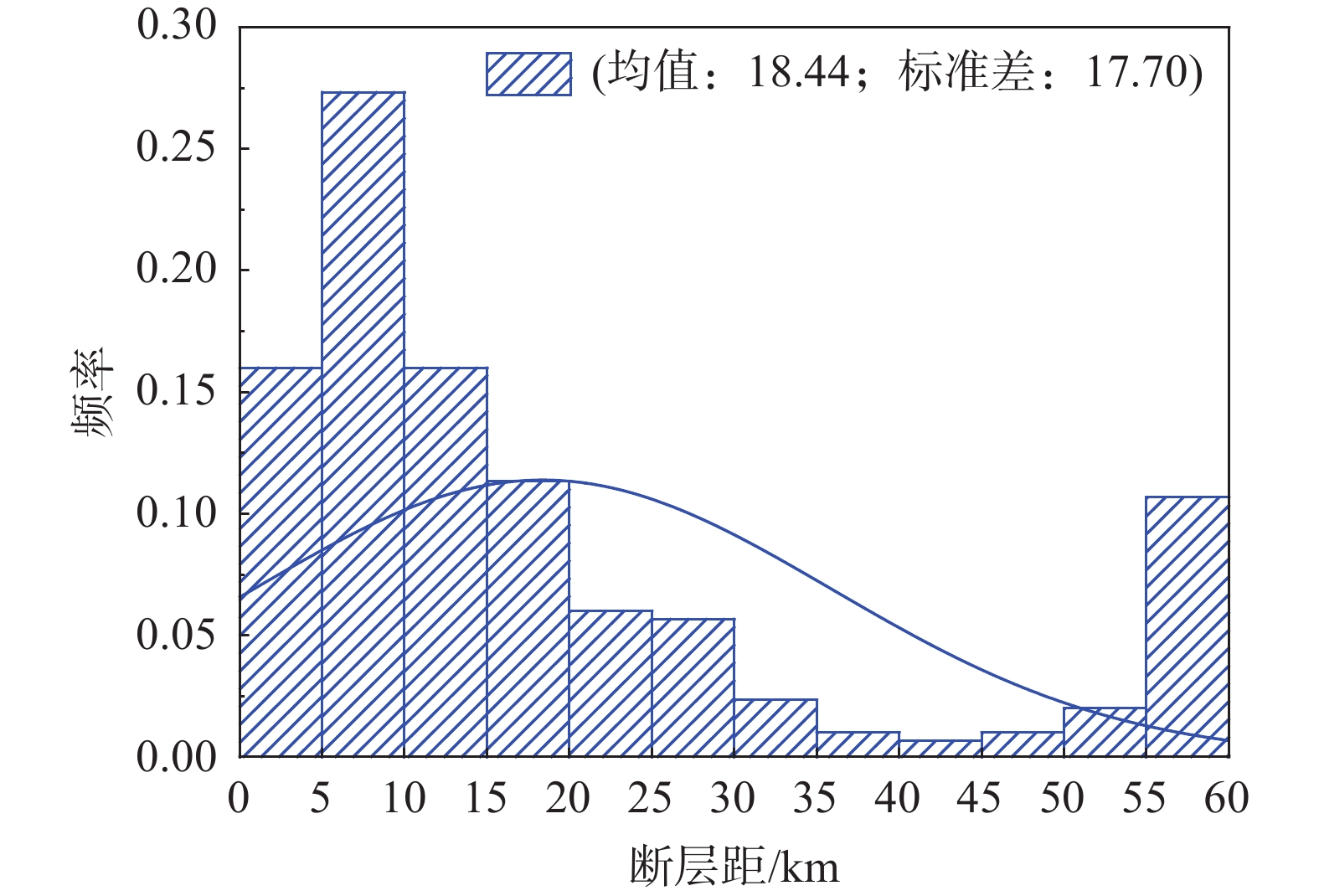
由于泸定县属于近断层地震高发区，距离磨西台地最近的鲜水河断裂带曾发生过多次强震。四川地震局的数据显示，1700年−2022年之间，鲜水河断裂带共发生了59次5.0以上地震，其中，6.0级~6.9级地震17次(含本次泸定地震)，7.0级~7.9级地震10次。该博物馆距离鲜水河断裂带不足5 km，为了更好地反映框架W2可能出现的震害，本文从the Pacific Earthquake Engineering Research (PEER) ground motion database选用300余组断层距不大于60 km的地震动记录(不包含本次泸定地震动记录)进行弹塑性时程分析，所选用地震记录的断层距的统计结果见图4。
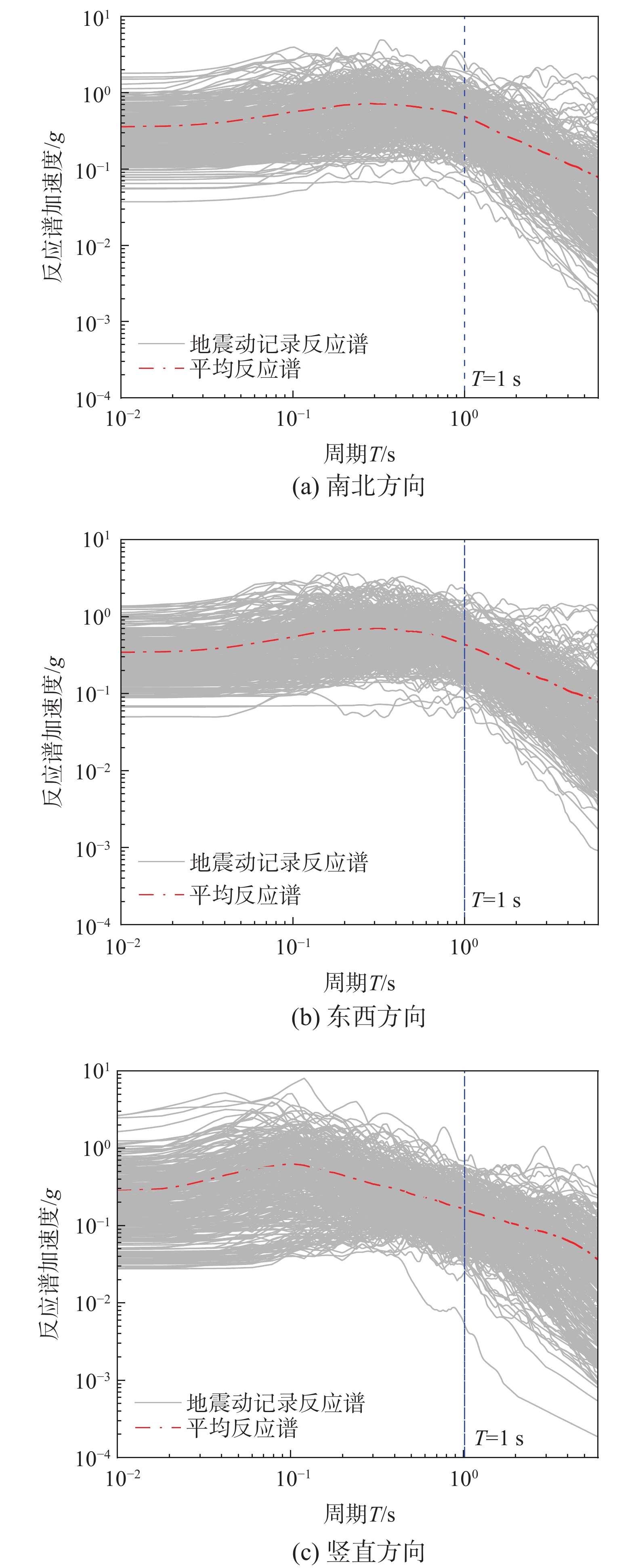
如图4所示，超过一半的地震动记录的断层距小于20 km，根据已有研究[22]，有90条地震动记录属于脉冲型地震，占比达到30%。本文所采用的地震动记录具备近断层地震的特性，能够代表框架W2所在场地潜在地震的特点。地震动记录各方向的反应谱和平均反应谱见图5。
本文考虑多元地震动参数对结构抗震能力和抗震需求的影响。根据已有研究[23 − 29]，地震动参数大体可分为三类：1)加速度相关参数；2)速度相关参数；3)位移相关参数。为考虑地震记录中可能出现的脉冲型地震的影响，同时考虑到框架W2的基本自振周期为0.43 s，属于中短周期结构，对位移相关参数不敏感。因此，本文选用三类地震动参数：脉冲相关参数，加速度相关参数和速度相关参数，共计17个常用的地震动参数作为抗震需求Kriging模型的输入参数。地震动多元参数及计算方法见表1。
表 1 地震动多元参数及计算方法Table 1. Multi-parameters of ground motion and the corresponding calculation methods编号 名称 符号 计算方法 脉冲相关参数 1 脉冲周期/s TP 采用文献[30]中的计算方法 2 脉冲因子 PI {[ {1 + \exp ( { - 23.3 + 14.6{\rm PG{V}_{{\text{ratio}}}} + 20.5{E_{{\text{ratio}}}}} )} ]^{ - 1}} 3 脉冲幅值/(cm/s) Ap \max | {{{\dot u}_g}(t)} | 加速度相关参数 1 地震动峰值加速度/g PGA \max | {{{\ddot u}_g}(t)} | 2 第一阶周期谱加速度/g Sa(T1) | {{S_{\rm{a}}}( {{T_1}} )} | 3 加速度反应谱峰值/g Sa,max \max | {{S_{\rm{a}}}( {{T_1}} )} | 4 有效峰值加速度/g EPA \dfrac{{{S_{\rm{a}}}(T = 0.2\;{\rm s})}}{{2.5}} 5 Riddell指标 Ia {\rm PGV}{( {{t_{95}} - {t_5}} )^{1/3}} 6 Housner强度/g2 Pa \dfrac{1}{t_{95}-t_5}\displaystyle\int_{t_5}^{t_{95}}[\ddot{u}_g(t)]^2\mathrm{d}t 7 Arias强度/(cm/s) IA \dfrac{\pi}{2g}\displaystyle\int_0^{T_{\rm f}}[\ddot{u}_g(t)]^2\mathrm{d}t 8 Park-Ang指标 IC P_{\rm{a}}^{0.75}{( {{t_{95}} - {t_5}} )^{0.5}} 速度相关参数 1 最大正负速度峰值差/(cm/s) PPV \max ( {{{\dot u}_g}(t)} ) - \min ( {{{\dot u}_g}(t)} ) 2 速度反应谱峰值/(cm/s) Sv,max \max | {{S_{\mathrm{v}}}(T)} | 3 Housner强度/(cm2/s2) Pv \dfrac{1}{t_{95}-t_5}\displaystyle\int_{t_5}^{t_{95}}[\dot{u}_g(t)]^2\mathrm{d}t 4 修正的Arias强度/(cm·s) Imia {I_{\mathrm{A}}}/{v_{0}^2} 5 Riddell指标 Iv {\rm PG{V}^{2/3}}{( {{t_{95}} - {t_5}} )^{1/3}} 6 Faifar指标 IF {\rm PG{V}^{2/3}}{( {{t_{95}} - {t_5}} )^{1/4}} 注：PGVratio为提取出脉冲信号后剩余波形信号与原记录PGV之比；Eratio为剩余波形信号的能量与原始记录能量的比值，该比值大于0.85时为脉冲型，小于0.15时为非脉冲型； {\ddot u_g}(t) 和 {\dot u_g}(t) 分别为地震动记录的加速度与速度时程； {S_{\rm{a}}} 和 {S_{\mathrm{v}}} 分别为地震动记录的反应谱加速度与速度；T为结构自振周期；t5和t95分别为计算所得Arias强度分别占整个地震结束时刻计算所得Arias强度的5%和95%的对应时刻；Tf为地震动总持时；v0为地震动加速度曲线在单位时间内通过零点的次数。 3.3 地震动参数重要性分析
根据有限元弹塑性时程分析结果，采用LASSO正则化方法对地震动参数进行分析，并采用归一化后的回归系数向量 \text{γ} 作为地震动参数重要性的量化指标。水平和竖直三个方向(南北方向为X向，东西方向为Y向，竖直方向为Z向)上17个地震动参数对于框架W2首层、二层最大层间位移角和基底剪力的重要性分析结果见图6。
![]()
图 6 地震动参数重要性分析结果Figure 6. Analysis results of the importance of ground motion parameters如图6所示，从整体上看，地震动参数与结构响应均呈正相关，且速度相关参数的影响最大。其中，影响框架W2最大层间位移角的主要参数是水平方向的反应谱速度；影响框架W2基底剪力的地震动参数较多，竖直方向的Riddell指标对框架W2的基底剪力产生的影响最大，除了与速度相关的地震动参数，脉冲周期和有效加速度对基底剪力也产生了较大影响。
3.4 训练数据
本文对抗震能力Kriging模型和抗震需求Kriging模型分别进行训练：抗震能力Kriging模型用来建立结构的能力曲线，输入输出参数分别为框架W2的基底剪力和最大层间位移角；抗震需求Kriging模型用来模拟地震作用下结构的响应，输入地震动参数，输出框架W2的基底剪力和最大层间位移角。由于离群数据对K-means聚类算法的聚类效果影响较大[18]，本文从300余组地震动参数数据中剔除离群数据，用于训练Kriging模型的地震动参数频率分布直方图和最大层间位移角、基底剪力的频率分布直方图见图7~图10。
![]()
图 7 脉冲相关参数频率分布直方图Figure 7. Histogram of pulse-related parameter frequency distributions如图7~图10所示，从整体上看，地震动参数和结构地震响应的波动性比较大，地震动的竖向分量较为显著，但各强度指标仍小于水平方向的各强度指标，统计结果与近断层地震的特点相符[21]。在选用的地震动作用下，框架W2最大层间位移角超过1/550的情况，占比多于最大层间位移角小于等于1/550的情况，框架W2最大层间位移角的最大值达到了1/79，训练数据覆盖了结构从弹性到弹塑性状态的响应。
![]()
图 8 加速度相关参数频率分布直方图Figure 8. Histogram of acceleration-related parameter frequency distributions![]()
图 9 速度相关参数频率分布直方图Figure 9. Histogram of speed-related parameter frequency distributions![]()
图 10 最大层间位移角和基底剪力频率分布直方图Figure 10. Histograms of maximum interstorey displacement angle and base shear frequency distribution4 Kriging模型的训练
4.1 抗震能力曲线
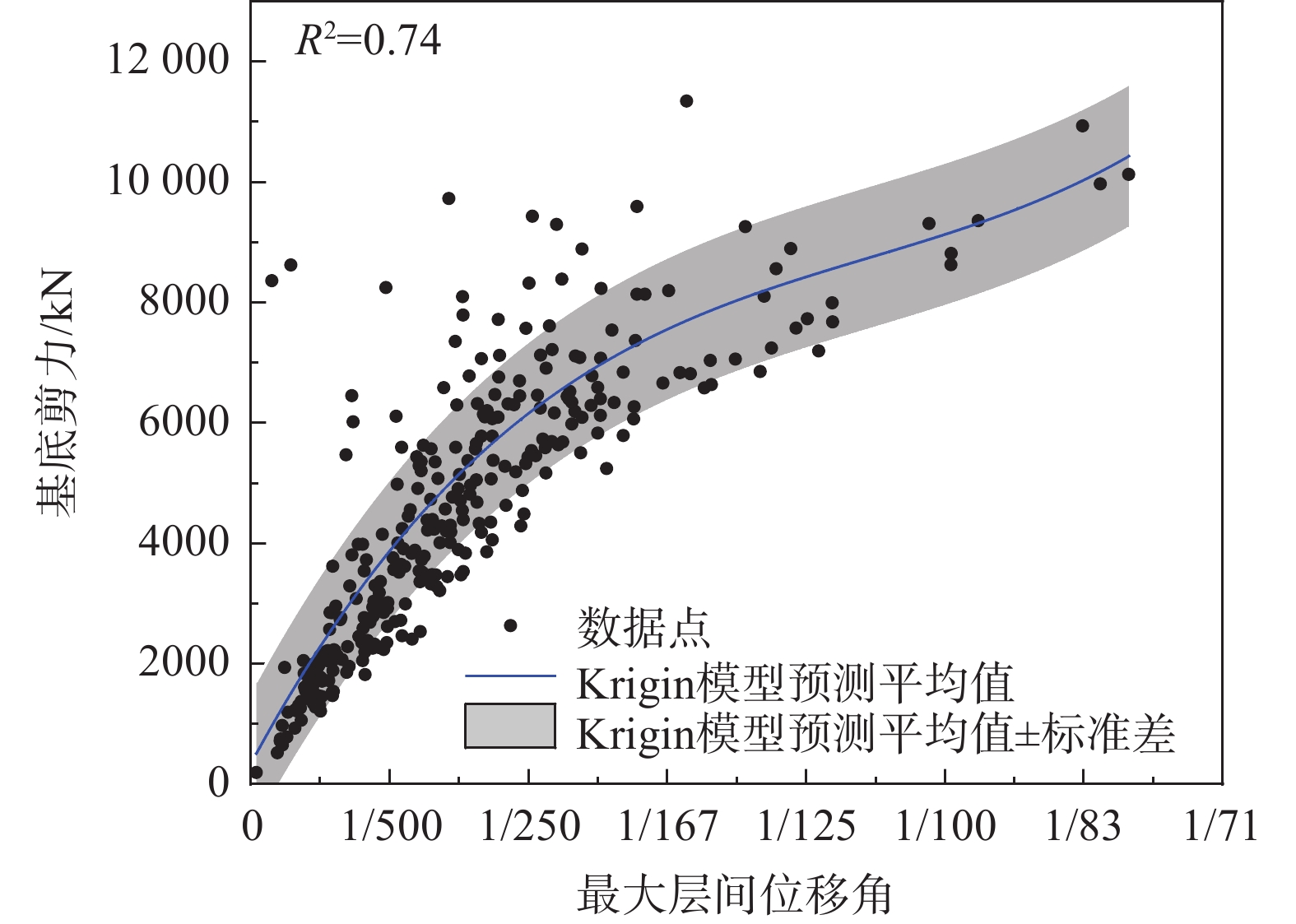
根据第2节所述，采用从弹塑性时程分析得到的300组基底剪力-最大层间位移角的数据训练Kriging模型，并拟合生成框架W2的抗震能力曲线。训练中数据进行归一化处理，均值函数设为三次多项式，相关函数采用Matern函数。相比采用传统的对数据进行拟合求解抗震能力方程的方法，由于不需要假定能力曲线的方程形式，根据抗震能力Kriging模型得到的抗震能力曲线更准确。框架W2的抗震能力曲线见图11。如图所示，框架W2的抗震能力曲线可分为：线性段—斜率下降段—斜率上升段，三个阶段。斜率上升是由于结构变形过大，计算结果不收敛造成的，本文中斜率开始上升对应的最大层间位移角定义为失效状态的最大层间位移角临界值，三个阶段分别对应结构的弹性，弹塑性和失效状态。根据本文第2节中的震害分级标准，可得框架W2震害等级对应的最大层间位移角限值，见表2。
平面布置不规则，梁柱节点设计不合理，框架柱截面尺寸偏小，框架W2的柱底箍筋加密区的箍筋配置不足等因素[21]，导致了框架W2变形能力较差。如表2所示，框架W2的屈服最大层间位移角小于规范规定的一般框架结构弹性层间位移角限值1/550，同时极限层间位移角也要小于一般框架结构弹塑性层间位移角的限值1/50。鉴于框架W2各个震害等级的限值的波动性较小，尤其当震害等级达到LS后，三条曲线对应的层间位移角限值趋于一致，因此本文采用抗震能力曲线的均值作为框架W2最终的抗震能力曲线。
表 2 框架W2各震害等级对应的层间位移角限值Table 2. Displacement angle limits for frame W2 damage levels抗震能力曲线 层间位移角限值 OP IO LS CP (μ-σ)曲线 1/1489 1/477 1/136 1/112 μ曲线 1/1605 1/481 1/136 1/112 (μ+σ)曲线 1/1100 1/455 1/133 1/112 注：μ和σ分别为抗震能力曲线的均值和标准差。 4.2 抗震需求Kriging模型
本文将弹塑性时程分析数据按80%∶20%的比例分为训练集和测试集，采用四种不同方式分别对Kriging模型进行训练。模型1：仅将图6中的重要地震动参数(采用的重要地震动参数为：Sv,max, PPV, Iv, Tp, IF)作为数据的特征，训练得到抗震需求Kriging模型；模型2：将表1中的全部地震动参数作为数据的特征，训练得到抗震需求Kriging模型；模型3：采用K-means聚类算法将全部数据分为两簇后，选出与泸定地震动参数最为接近的数据，并且仅将图6中的重要地震动参数作为数据的特征，训练得到抗震需求Kriging模型；模型4：采用K-means聚类算法将全部数据分为两簇后，选出与泸定地震动参数最为接近的数据，并且将表1中的全部地震动参数作为数据的特征，训练得到抗震需求Kriging模型。训练四个Kriging模型时，将数据进行归一化处理，均值函数设为常数0，相关函数采用Matern函数。另外，同样将300组时程分析的结果，按80%∶20%的比例分为训练集和测试集，采用HAZUS法中的概率抗震需求分析方法[2]，以结构主方向的第一周期谱加速度作为地震动强度表征参数，计算得到PSDM(Probabilistic seismic demand model)。四个抗震需求Kriging模型和PSDM计算出的均值的准确性见表3。
近断层地震的地震动参数的不确定性较大导致抗震需求计算结果不确定性增大，进而使得四个抗震需求Kriging模型和PSDM均值的准确率降低。如表3所示，模型1和模型2的模拟准确性较为接近，模型1的偏差率更小，LASSO正则化方法能够提高Kriging模型的准确性。相比之下，由于模型3和模型4训练数据量较少，分类后可用于训练的数据不足，模型3和模型4的准确性稍差，同时确定系数R2数值也较小，但四个模型的平均偏差率均小于50%。PSDM计算出的首层、二层最大层间位移角的平均偏差分别比模型1大33%和32.5%，准确性低于四个抗震需求Kriging模型，且确定系数R2数值最小。 由于每一次训练会随机划分训练集与测试集，模型1~模型4的模拟结果存在一定的波动性，但整体波动范围在5%以内，不影响最终抗震预估结果。
表 3 不同抗震需求模型的偏差率Table 3. Deviation rate of different seismic demand models抗震需求
模型首层最大层间位移角 二层最大层间位移角 基底剪力 平均偏差/
(%)R2 平均偏差/
(%)R2 平均偏差/
(%)R2 模型1 45 0.58 43 0.57 33 0.49 模型2 46 0.57 45 0.56 33 0.66 模型3 48 0.36 45 0.36 44 0.43 模型4 46 0.36 44 0.38 42 0.44 PSDM 60 0.25 57 0.25 40 0.33 注：平均偏差是与有限元模型结果偏差的平均值。 5 震害预估方法的验证
5.1 框架W2的实际震害
由于台地效应和竖向地震显著等不利因素的影响，再加之框架W2的平面布置不规则，在本次泸定地震中，框架W2出现了严重破坏[21]：首层大量梁柱节点出现塑性铰，首层框架柱下端出现弯剪、受压破坏，首层和二层楼板发生了整体倾斜，产生的高差达到了38 cm左右。专家对框架W2进行调查后，将其认定为不安全，震害等级超过了CP，即结构出现垮塌。框架W2的典型震害见图12~图14。
![]()
图 12 框架W2首层梁柱节点典型震害(拍摄：潘毅)Figure 12. Typical seismic damage of beam-column joints in the first floor of frame W2![]()
图 13 框架W2首层框架柱柱底典型震害(拍摄：潘毅)Figure 13. Typical seismic damage at the bottom of columns in the first floor of frame W25.2 SC.V2204台站地震动记录参数
本文采用泸定SC.V2204台站的地震动记录对本文中的震害预估方法进行验证，并考虑台地效应对地震动的放大作用[21]，地震动记录的具体调整方法详文献[21]。SC.V2204台站的地震动记录具有较强的近断层脉冲属性[21]，地震动记录的三个方向的加速度时程曲线及详细信息见文献[21]。放大后的泸定SC.V2204台站的归一化地震动参数，见图15。如图所示，放大后的SC.V2204台站的地震动参数的各强度指标数值均处于训练数据的最大值和最小值之间，训练数据能够将需要预测地震的地震动参数包络，抗震需求Kriging模型的预测结果具备可信性。
![]()
图 15 训练数据分布区间与放大后的SC.V2204台站地震动记录参数Figure 15. Training data range and amplified ground motion parameters of SC.V2204 station5.3 震害预估结果与实际震害的对比
本文将SC.V2204台站地震动记录按实际地形影响放大后，分别将地震动参数输入抗震需求Kriging模型和PSDM，计算框架W2的抗震需求；采用放大后的地震动记录进行时程分析，并将有限元分析结果作为结构抗震需求的真实值。在放大后的SC.V2204台站地震动记录作用下，框架W2整体结构的最大层间位移角出现在首层。框架W2的抗震需求结果见表4。
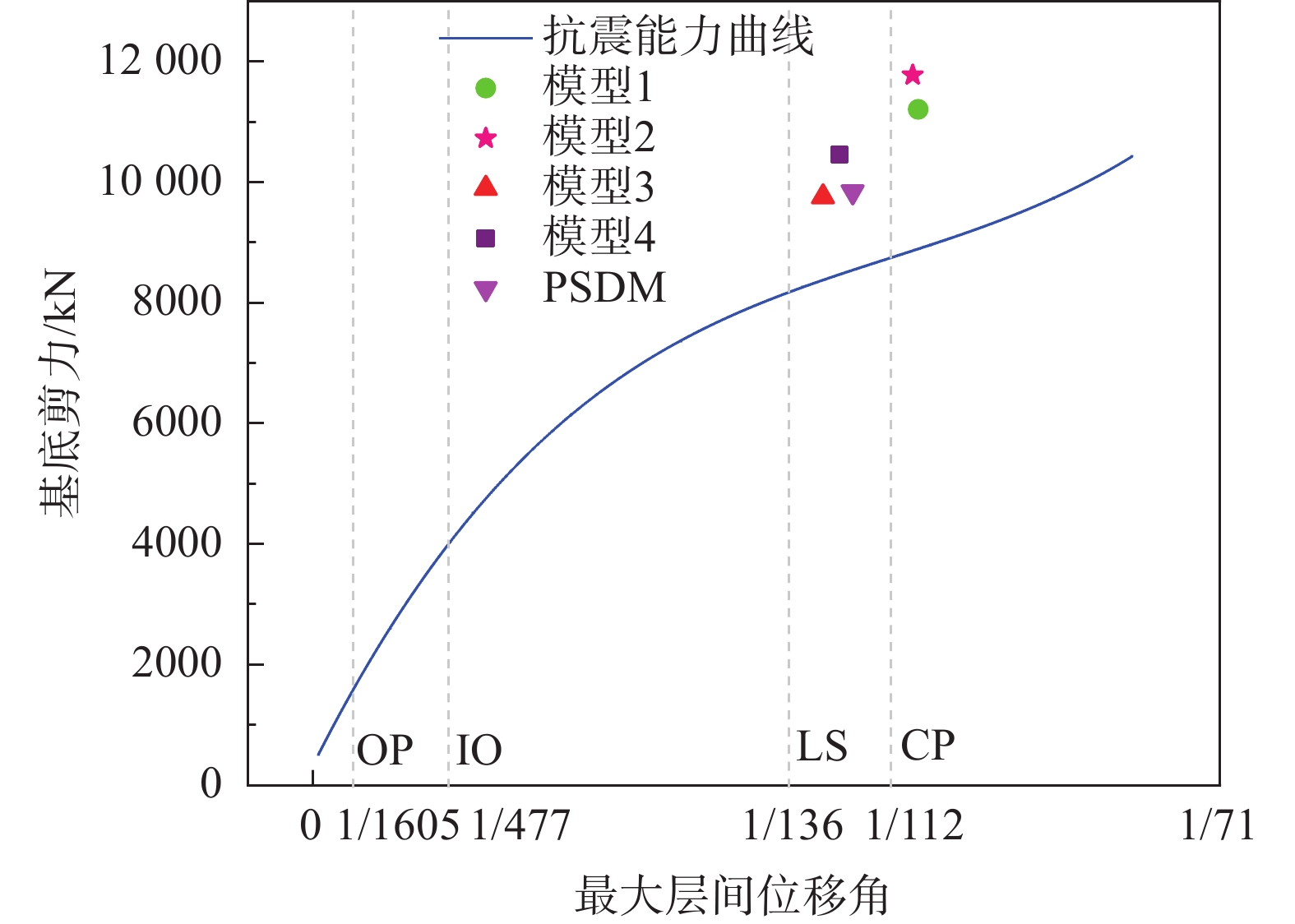
表 4 框架W2的抗震需求计算结果Table 4. Prediction results of seismic demand of frame W2抗震需求模型 最大层间位移角 基底剪力 μ σ COV μ/kN σ/kN COV 模型1 1/229 1/403 0.57 4542.27 3334.20 0.73 模型2 1/231 1/403 0.57 5946.98 2916.72 0.49 模型3 1/213 1/619 0.34 6072.18 1844.37 0.30 模型4 1/262 1/467 0.56 5109.30 2673.94 0.58 PSDM 1/223 1/516 0.43 5938.50 1950.47 0.33 注：μ和σ分别为抗震需求的均值和标准差；COV为变异系数。 如表4所示，对于最大层间位移角，四个抗震需求Kriging模型的计算结果的标准差与训练数据的最大层间位移角的标准差处于同一水平，见图10。同时四个模型计算出的最大层间位移角的变异系数均处于0.3~0.6，波动性与已有研究结论[31 − 32]相符。此外，四个抗震需求Kriging模型的标准差均大于PSDM计算出的标准差，当采用多元参数进行结构抗震需求计算时，由于考虑了各多参数的不确定性，导致最终抗震需求结果的不确定性增大。对于基底剪力，除模型1以外，其余模型计算结果的变异系数同样处于0.3~0.6。为计入结构地震响应的不确定性，本文采用具有95%保证率的最大层间位移角和基底剪力作为抗震需求的标准值。框架W2在泸定地震中震害的预估结果见图16。
如图16所示，模型1和模型2的结果与实际震害相符，均能准确预估结构在地震中会出现垮塌；模型3和模型4的结果准确性较差，低估了实际震害，可知训练数据量对Kriging模型的准确性起到了重要作用，而当数据量不足时，传统K-means聚类算法不能有效的提高结果的准确性。PSDM同样低估了实际震害，采用单参数的评估方法的准确性尚不能达到工程需求。
综上，当采用300个训练数据时，本文中基于Kriging模型的抗震预估方法能够准确的预估框架W2在地震中出现的震害。相比HAZUS法，基于Kriging模型的抗震预估方法从概念上更为直接，同时准确性也更能得到保证。对于地震救援任务较为复杂的山区中的一些重点结构，例如，学校、政府机构等，可以将训练好的Kriging模型与结构设计图纸共同交付相关部门，以便震后快速、针对性的开展救援活动。
6 结论
本文建立了基于Kriging模型的震害预估方法：采用300余组地震动记录的时程分析结果对Kriging模型进行训练，并采用LASSO正则化方法作为特征选择方法，结合K-means聚类算法，提高Kriging模型的训练效率和准确性。最后根据位于泸定县摩西台地某博物馆的多层框架结构的实际震害对提出的方法进行了验证。根据本文的研究结果，可以得到以下三点结论：
(1)采用泸定县某多层框架结构的实际震害对基于Kriging模型的震害预估方法进行了验证，当采用300个训练数据时，基于Kriging模型的震害预估方法能够满足工程需求，可以作为HAZUS法改进的参考；
(2)训练数据量对Kriging模型的准确性起到了重要作用。在数据有限的情况下，特征选择方法可以提高Kriging模型的准确性，但K-means聚类算法并不能有效的提高结果的准确性；
(3)地震动参数对结构响应的影响较为复杂，因此对数据量的需求较大，训练数据获取成本较高是Kriging模型在结构抗震领域应用的限制因素。
-
![]()
图 1 基于Kriging模型的震害预估流程图
Figure 1. Flow chart of seismic damage prediction based on Kriging surrogate model
![]()
图 2 FEMA356抗震能力曲线示意[17]
Figure 2. Schematic diagram of seismic capacity curve in FEMA356
![]()
图 6 地震动参数重要性分析结果
Figure 6. Analysis results of the importance of ground motion parameters
![]()
图 7 脉冲相关参数频率分布直方图
Figure 7. Histogram of pulse-related parameter frequency distributions
![]()
图 8 加速度相关参数频率分布直方图
Figure 8. Histogram of acceleration-related parameter frequency distributions
![]()
图 9 速度相关参数频率分布直方图
Figure 9. Histogram of speed-related parameter frequency distributions
![]()
图 10 最大层间位移角和基底剪力频率分布直方图
Figure 10. Histograms of maximum interstorey displacement angle and base shear frequency distribution
![]()
图 12 框架W2首层梁柱节点典型震害(拍摄：潘毅)
Figure 12. Typical seismic damage of beam-column joints in the first floor of frame W2
![]()
图 13 框架W2首层框架柱柱底典型震害(拍摄：潘毅)
Figure 13. Typical seismic damage at the bottom of columns in the first floor of frame W2
![]()
图 15 训练数据分布区间与放大后的SC.V2204台站地震动记录参数
Figure 15. Training data range and amplified ground motion parameters of SC.V2204 station
表 1 地震动多元参数及计算方法
Table 1 Multi-parameters of ground motion and the corresponding calculation methods
编号 名称 符号 计算方法 脉冲相关参数 1 脉冲周期/s TP 采用文献[30]中的计算方法 2 脉冲因子 PI {[ {1 + \exp ( { - 23.3 + 14.6{\rm PG{V}_{{\text{ratio}}}} + 20.5{E_{{\text{ratio}}}}} )} ]^{ - 1}} 3 脉冲幅值/(cm/s) Ap \max | {{{\dot u}_g}(t)} | 加速度相关参数 1 地震动峰值加速度/g PGA \max | {{{\ddot u}_g}(t)} | 2 第一阶周期谱加速度/g Sa(T1) | {{S_{\rm{a}}}( {{T_1}} )} | 3 加速度反应谱峰值/g Sa,max \max | {{S_{\rm{a}}}( {{T_1}} )} | 4 有效峰值加速度/g EPA \dfrac{{{S_{\rm{a}}}(T = 0.2\;{\rm s})}}{{2.5}} 5 Riddell指标 Ia {\rm PGV}{( {{t_{95}} - {t_5}} )^{1/3}} 6 Housner强度/g2 Pa \dfrac{1}{t_{95}-t_5}\displaystyle\int_{t_5}^{t_{95}}[\ddot{u}_g(t)]^2\mathrm{d}t 7 Arias强度/(cm/s) IA \dfrac{\pi}{2g}\displaystyle\int_0^{T_{\rm f}}[\ddot{u}_g(t)]^2\mathrm{d}t 8 Park-Ang指标 IC P_{\rm{a}}^{0.75}{( {{t_{95}} - {t_5}} )^{0.5}} 速度相关参数 1 最大正负速度峰值差/(cm/s) PPV \max ( {{{\dot u}_g}(t)} ) - \min ( {{{\dot u}_g}(t)} ) 2 速度反应谱峰值/(cm/s) Sv,max \max | {{S_{\mathrm{v}}}(T)} | 3 Housner强度/(cm2/s2) Pv \dfrac{1}{t_{95}-t_5}\displaystyle\int_{t_5}^{t_{95}}[\dot{u}_g(t)]^2\mathrm{d}t 4 修正的Arias强度/(cm·s) Imia {I_{\mathrm{A}}}/{v_{0}^2} 5 Riddell指标 Iv {\rm PG{V}^{2/3}}{( {{t_{95}} - {t_5}} )^{1/3}} 6 Faifar指标 IF {\rm PG{V}^{2/3}}{( {{t_{95}} - {t_5}} )^{1/4}} 注：PGVratio为提取出脉冲信号后剩余波形信号与原记录PGV之比；Eratio为剩余波形信号的能量与原始记录能量的比值，该比值大于0.85时为脉冲型，小于0.15时为非脉冲型； {\ddot u_g}(t) 和 {\dot u_g}(t) 分别为地震动记录的加速度与速度时程； {S_{\rm{a}}} 和 {S_{\mathrm{v}}} 分别为地震动记录的反应谱加速度与速度；T为结构自振周期；t5和t95分别为计算所得Arias强度分别占整个地震结束时刻计算所得Arias强度的5%和95%的对应时刻；Tf为地震动总持时；v0为地震动加速度曲线在单位时间内通过零点的次数。 
下载: 导出CSV
表 2 框架W2各震害等级对应的层间位移角限值
Table 2 Displacement angle limits for frame W2 damage levels
抗震能力曲线 层间位移角限值 OP IO LS CP (μ-σ)曲线 1/1489 1/477 1/136 1/112 μ曲线 1/1605 1/481 1/136 1/112 (μ+σ)曲线 1/1100 1/455 1/133 1/112 注：μ和σ分别为抗震能力曲线的均值和标准差。
下载: 导出CSV
表 3 不同抗震需求模型的偏差率
Table 3 Deviation rate of different seismic demand models
抗震需求
模型首层最大层间位移角 二层最大层间位移角 基底剪力 平均偏差/
(%)R2 平均偏差/
(%)R2 平均偏差/
(%)R2 模型1 45 0.58 43 0.57 33 0.49 模型2 46 0.57 45 0.56 33 0.66 模型3 48 0.36 45 0.36 44 0.43 模型4 46 0.36 44 0.38 42 0.44 PSDM 60 0.25 57 0.25 40 0.33 注：平均偏差是与有限元模型结果偏差的平均值。
下载: 导出CSV
表 4 框架W2的抗震需求计算结果
Table 4 Prediction results of seismic demand of frame W2
抗震需求模型 最大层间位移角 基底剪力 μ σ COV μ/kN σ/kN COV 模型1 1/229 1/403 0.57 4542.27 3334.20 0.73 模型2 1/231 1/403 0.57 5946.98 2916.72 0.49 模型3 1/213 1/619 0.34 6072.18 1844.37 0.30 模型4 1/262 1/467 0.56 5109.30 2673.94 0.58 PSDM 1/223 1/516 0.43 5938.50 1950.47 0.33 注：μ和σ分别为抗震需求的均值和标准差；COV为变异系数。
下载: 导出CSV
-
[1] 潘毅, 范元青, 任宇, 等. 芦山6.1级地震山区典型震害调查与分析[J]. 土木工程学报, 2023, 56(12): 35 − 48. PAN Yi, FAN Yuanqing, REN Yu, et al. Typical seismic damage investigation and analysis in Mountain area after MS6.1 Lushan earthquake [J]. China Civil Engineering Journal, 2023, 56(12): 35 − 48. (in Chinese)
[2] 陈颙, 陈运泰, 张国民, 等. “十一·五”期间中国重大地震灾害预测预警和防治对策[J]. 灾害学, 2005, 20(1): 1 − 14. doi: 10.3969/j.issn.1000-811X.2005.01.001 CHEN Yong, CHEN Yuntai, ZHANG Guomin, et al. Forecast and early-warning and preparedness measures for great earthquake disasters in China during the period of the 11th Five-year Plan [J]. Journal of Catastrophology, 2005, 20(1): 1 − 14. (in Chinese) doi: 10.3969/j.issn.1000-811X.2005.01.001
[3] 潘毅, 袁家聪, 林拥军, 等. 泸定6.8级地震农村居住建筑震害调查与分析[J]. 防灾减灾工程学报, 2023, 43(6): 1200 − 1214. PAN Yi, YUAN Jiacong, LIN Yongjun, et al. Seismic damage investigation and analysis of rural residential buildings in MS6.8 Luding earthquake [J]. Journal of Disaster Prevention and Mitigation Engineering, 2023, 43(6): 1200 − 1214. (in Chinese)
[4] FEMA. Multi-hazard loss estimation methodology, earthquake model (HAZUS-MHMR4) [R]. Washington DC: Federal Emergency Management Agency, 2003.
[5] 于晓辉, 吕大刚. HAZUS相容的钢筋混凝土框架结构地震易损性分析[J]. 工程力学, 2016, 33(3): 152 − 160. doi: 10.6052/j.issn.1000-4750.2014.08.0685 YU Xiaohui, LYU Dagang. HAZUS-compatible seismic fragility analysis for rc frame structures [J]. Engineering Mechanics, 2016, 33(3): 152 − 160. (in Chinese) doi: 10.6052/j.issn.1000-4750.2014.08.0685
[6] 林世镔, 谢礼立, 公茂盛, 等. 城市建筑物抗震能力评估方法[J]. 自然灾害学报, 2011, 20(4): 31 − 37. LIN Shibin, XIE Lili, GONG Maosheng, et al. Methodology for estimating seismic capacity of city building [J]. Journal of Natural Disasters, 2011, 20(4): 31 − 37. (in Chinese)
[7] 陈洪富, 孙柏涛, 陈相兆, 等. HAZ-China地震灾害损失评估系统研究[J]. 土木工程学报, 2013, 46(增刊2): 294 − 300. CHEN Hongfu, SUN Baitao, CHEN Xiangzhao, et al. HAZ-China earthquake disaster loss estimation system [J]. China Civil Engineering Journal, 2013, 46(Suppl 2): 294 − 300. (in Chinese)
[8] 程庆乐, 曾翔, 熊琛, 等. 区域建筑震害模拟方法分析对比[J]. 工程力学, 2017, 34(增刊1): 105 − 110, 128. doi: 10.6052/j.issn.1000-4750.2016.03.S014 CHENG Qingle, ZENG Xiang, XIONG Chen, et al. Comparison of seismic damage simulation methods for different regional buildings [J]. Engineering Mechanics, 2017, 34(Suppl 1): 105 − 110, 128. (in Chinese) doi: 10.6052/j.issn.1000-4750.2016.03.S014
[9] BERNARDINI E, SPENCE S M J, WEI D, et al. Aerodynamic shape optimization of civil structures: A CFD-enabled Kriging-based approach [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 144: 154 − 164. doi: 10.1016/j.jweia.2015.03.011
[10] GIDARIS I, TAFLANIDIS A A, MAVROEIDIS G P. Kriging metamodeling in seismic risk assessment based on stochastic ground motion models [J]. Earthquake Engineering & Structural Dynamics, 2015, 44(14): 2377 − 2399.
[11] JIA G F, TAFLANIDIS A A. Kriging metamodeling for approximation of high-dimensional wave and surge responses in real-time storm/hurricane risk assessment [J]. Computer Methods in Applied Mechanics and Engineering, 2013, 261/262: 24 − 38. doi: 10.1016/j.cma.2013.03.012
[12] LI M, WANG R Q, JIA G F. Efficient dimension reduction and surrogate-based sensitivity analysis for expensive models with high-dimensional outputs [J]. Reliability Engineering & System Safety, 2020, 195: 106725.
[13] KYPRIOTI A P, TAFLANIDIS A A. Kriging metamodeling for seismic response distribution estimation [J]. Earthquake Engineering & Structural Dynamics, 2021, 50(13): 3550 − 3576.
[14] 韩忠华. Kriging模型及代理优化算法研究进展[J]. 航空学报, 2016, 37(11): 3197 − 3225. HAN Zhonghua. Kriging surrogate model and its application to design optimization: A review of recent progress [J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(11): 3197 − 3225. (in Chinese)
[15] 常泽明, 李璐祎. 基于NARX和Kriging的时变可靠性分析双层代理模型[J]. 北京航空航天大学学报, 2023, 49(7): 1802 − 1812. CHANG Zeming, LI Luyi. Double-loop surrogate model for time-dependent reliability analysis based on NARX and Kriging models [J]. Journal of Beijing University of Aeronautics and Astronautics, 2023, 49(7): 1802 − 1812. (in Chinese)
[16] 赵海龙, 岳珠峰, 刘伟. 矩独立重要性分析的Kriging代理模型方法[J]. 航空学报, 2016, 37(7): 2234 − 2241. ZHAO Hailong, YUE Zhufeng, LIU Wei. A Kriging surrogate model method for moment-independent importance analysis [J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(7): 2234 − 2241. (in Chinese)
[17] 任靖哲, 黄细军, 曾晗, 等. Y型铸钢节点抗压承载力设计方法研究[J]. 工业建筑, 2024, 54(4): 81 − 89. doi: 10.3724/j.gyjzG21110904 REN Jingzhe, HUANG Xijun, ZENG Han, et al. Research on the design method of compressive bearing capacity of Y-type cast steel joints [J]. Industrial Construction, 2024, 54(4): 81 − 89. (in Chinese) doi: 10.3724/j.gyjzG21110904
[18] HARTIGAN J A, WONG M A. Algorithm AS 136: A K-means clustering algorithm [J]. Journal of the Royal Statistical Society, 1979, 28(1): 100 − 108.
[19] American Society of Civil Engineers. Prestandard and commentary for the seismic rehabilitation of buildings [S]. Washington DC: American Society of Civil Engineers, 2000.
[20] 汪梦甫, 周锡元. 高层建筑结构抗震弹塑性分析方法及抗震性能评估的研究[J]. 土木工程学报, 2003, 36(11): 44 − 49. doi: 10.3321/j.issn:1000-131X.2003.11.009 WANG Mengfu, ZHOU Xiyuan. Modified pushover analysis and seismic performance evaluation for tall building [J]. China Civil Engineering Journal, 2003, 36(11): 44 − 49. (in Chinese) doi: 10.3321/j.issn:1000-131X.2003.11.009
[21] 潘毅, 任靖哲, 任宇, 等. 考虑台地效应的泸定6.8级地震某框架结构震害调查与分析[J/OL]. 土木工程学报, 2023: 1 − 16. https://doi.org/10.15951/j.tmgcxb.23050358, 2023-07-24. PAN Yi, REN Jingzhe, REN Yu, et al. Seismic damage investigation and analysis of a frame structure in the Luding MS6.8 earthquake with platform effect [J/OL]. China Civil Engineering Journal, 2023: 1 − 16. https://doi.org/10.15951/j.tmgcxb.23050358, 2023-07-24. (in Chinese)
[22] BAKER J W. Quantitative classification of near-fault ground motions using wavelet analysis [J]. Bulletin of the Seismological Society of America, 2007, 97(5): 1486 − 1501. doi: 10.1785/0120060255
[23] 翟长海, 谢礼立. 估计和比较地震动潜在破坏势的综合评述[J]. 地震工程与工程振动, 2002, 22(5): 1 − 7. doi: 10.3969/j.issn.1000-1301.2002.05.001 ZHAI Changhai, XIE Lili. A comprehensive method for estimating and comparing the damage potential of strong ground motion [J]. Earthquake Engineering and Engineering Vibration, 2002, 22(5): 1 − 7. (in Chinese) doi: 10.3969/j.issn.1000-1301.2002.05.001
[24] 朱瑞广, 吕大刚. 基于Copula函数的主余震地震动强度参数相关性分析[J]. 工程力学, 2019, 36(2): 114 − 123. doi: 10.6052/j.issn.1000-4750.2017.12.0921 ZHU Ruiguang, LYU Dagang. Copula-based correlation analysis of intensity measures of mainshock-aftershock ground motions [J]. Engineering Mechanics, 2019, 36(2): 114 − 123. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.12.0921
[25] 刘亭亭, 于晓辉, 吕大刚. 地震动多元强度参数主成分与结构损伤的相关性分析[J]. 工程力学, 2018, 35(8): 122 − 129, 137. doi: 10.6052/j.issn.1000-4750.2017.04.0289 LIU Tingting, YU Xiaohui, LYU Dagang. Analysis of correlation between principal components of multivariate earthquake intensity measures and structural damage [J]. Engineering Mechanics, 2018, 35(8): 122 − 129, 137. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.04.0289
[26] 赵晓芬, 温增平, 陈波, 等. 适用于全周期结构的速度脉冲型地震动强度表征参数研究[J]. 地震学报, 2019, 41(4): 536 − 547. doi: 10.11939/jass.20190002 ZHAO Xiaofen, WEN Zengping, CHEN Bo, et al. Intensity measures of pulse-like ground motions in the full periods [J]. Acta Seismologica Sinica, 2019, 41(4): 536 − 547. (in Chinese) doi: 10.11939/jass.20190002
[27] 郑志, 王勇, 温卫平, 等. 基于机器学习的核电厂震后损伤评估及响应预测方法[J/OL]. 工程力学, 2024: 1 − 13. http://kns.cnki.net/kcms/detail/11.2595.O3.20230731.1144.012.html, 2024-05-06. ZHENG Zhi, WANG Yong, WEN Weiping, et al. A machine learning-based approach to post-earthquake damage assessment and response prediction for nuclear power plants [J/OL]. Engineering Mechanics, 2024: 1 − 13[2024-05-06]. http://kns.cnki.net/kcms/detail/11.2595.O3.20230731.1144.012.html, 2024-05-06. (in Chinese)
[28] 王晓磊, 王浠铭, 阎卫东, 等. 基于Copula函数的水平和竖向地震动强度参数相关性分析[J]. 工程力学, 2023, 40(5): 79 − 92. doi: 10.6052/j.issn.1000-4750.2021.10.0812 WANG Xiaolei, WANG Ximing, YAN Weidong, et al. Correlation analysis of intensity measures of horizontal and vertical ground motions based on copula function [J]. Engineering Mechanics, 2023, 40(5): 79 − 92. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.10.0812
[29] KAZAZ İ, BILGE İ H, GÜRBÜZ M. Near-fault ground motion characteristics and its effects on a collapsed reinforced concrete structure in Hatay during the February 6, 2023 MW7.8 Kahramanmaraş earthquake [J]. Engineering Structures, 2024, 298: 117067. doi: 10.1016/j.engstruct.2023.117067
[30] 常志旺, 翟长海, 李爽, 等. 近场地震动速度脉冲周期的确定[J]. 土木工程学报, 2013, 46(增刊2): 130 − 134. CHANG Zhiwang, ZHAI Changhai, LI Shuang, et al. Determination of the pulse period for near-fault pulse-like ground motions [J]. China Civil Engineering Journal, 2013, 46(Suppl 2): 130 − 134. (in Chinese)
[31] Applied Technology Council. Quantification of building seismic performance factors[M]. US Department of Homeland Security, FEMA, 2009.
[32] RODRIGUEZ D, PERRONE D, FILIATRAULT A. Seismic demand on non‐structural elements for quantifying seismic performance factors [J]. Earthquake Engineering & Structural Dynamics, 2023, 52(4): 1016 − 1039.
计量
- 文章访问数: 51
- HTML全文浏览量: 21
- PDF下载量: 8
