黄土高填方区常常因地基不均匀沉降诱导建筑物产生倾斜、开裂现象^{[1 − 2]}，多采用微型钢管桩基础托换处理，但普通静压微型钢管桩钢管外侧直接与土体接触，受土体内盐分腐蚀严重。基于此，朱彦鹏等^[3]提出了一种高压注浆微型钢管桩，利用孔底高压返浆工艺形成钢管外侧保护层，其耐久性好，适合狭小空间施工，已在多项建筑基础托换工程中成功应用^{[4 − 5]}。然而，在黄土高填方场地中，微型钢管桩桩端需穿越较厚填土层后嵌入坚硬持力层，桩长一般较大，当填筑土体质量较差或遇水饱和时，桩体侧向约束较弱，具有极大的长细比，导致微型钢管桩的破坏模式除桩端土体局部剪切破坏以外，还容易发生桩体屈曲破坏。因此，有必要对该桩型在黄土高填方场地中的屈曲稳定性进行研究。

20世纪初，FORSESLL和GRANHOLM等分析认为：设置在极软弱地基中的细长桩应考虑其屈曲问题^[6]。之后，国内外学者开展了大量研究并给出了屈曲临界荷载的计算方法^{[7 − 9]}。赵明华等^[10]、杨健等^[11]、邹新军等^[12]分析表明桩侧正摩阻力对基桩屈曲稳定性的影响是极微的。范浩等^[13]给出了等截面压弯构件二阶效应的屈曲模态级数解。NADEEM等^[14]采用有限元方法分析了几何非线性与材料非线性对轴向荷载下端承桩屈曲特性的影响。HE等^[15]研究表明，屈曲破坏是深水软土地基中超长桩的一种破坏模式。

与大直径细长桩相比，黄土高填方场地建筑基础托换工程中的微型钢管桩桩体强度较高，长细比更大。对于完全嵌入的细长桩，其相对屈曲长度随桩体强度的增大而增大、长细比的增大而减小^[16]，并且桩侧土抗力与桩体刚度对屈曲挠曲线存在显著影响^[17]。因此，需对微型钢管桩的屈曲特性进一步研究。张小兵等^[18]通过黄土地区现场试验表明，超大长细比微型钢管桩容易发生屈曲破坏。SHIELDS^[19]指出，软弱地基中微型桩屈曲破坏已成为一个设计控制因素。VOGT等^[20]建议，通过现场桩基静载试验来确定微型桩屈曲破坏所对应的荷载设计值。朱彦鹏等^[21]以Winkler弹性地基梁理论为基础，给出了微型钢管桩屈曲临界荷载表达式。

上述研究对微型桩的屈曲破坏进行了深入分析。然而，目前基桩屈曲临界荷载计算方法均将桩侧土抗力按Winkler弹性地基梁处理，未考虑桩侧土体受力变形的连续性，即未考虑桩侧相邻土体间的剪切作用，因此计算结果与实际情况存在一定的差异。另外，在黄土高填方区，填筑土体固结沉降、湿陷变形及蠕变变形等会使微型桩桩侧产生负摩阻力，仍需讨论负摩阻力对其屈曲特性的影响。

基于此，本文针对黄土高填方区高压注浆微型钢管桩屈曲特性进行研究，以Pasternak双参数地基梁法为基础，试图给出考虑桩-土相互作用的微型钢管桩屈曲临界荷载计算方法，并讨论桩侧负摩阻力的影响，为其在建筑基础托换工程中的屈曲分析提供理论依据。

1   屈曲临界荷载的计算

1.1   高压注浆微型钢管桩简述

普通静压微型钢管桩仅钢管内填筑细石混凝土，钢管外壁直接与土体接触，受土壤内各种盐分腐蚀严重，且钢管外壁光滑，桩侧摩阻力较小，承载力较低。基于此，朱彦鹏等^[3]提出了一种高压注浆微型钢管桩及其施工方法，钢管由多根长度为1 m~1.5 m的钢管节利用自带螺纹连接而成，并利用孔底高压返浆工艺形成水泥砂浆保护层，可以有效避免钢管外壁受土体的腐蚀作用，提高其耐久性，如图1所示。

图  1  高压注浆微型钢管桩

Figure  1.  Threaded micro steel pipe pile with circular grouting at high pressure

下载: 全尺寸图片 幻灯片

高压注浆微型钢管桩施工步骤为：① 确定桩位，采用锚杆静压或坑式静压的方式将钢管逐节压入，其中第一桩节桩端设有桩尖、钢环箍及出浆孔，钢管压入后形成的桩孔大于钢管外径，间隙为15 mm~20 mm；② 待桩端到达设计深度后，将水泥砂浆加压后从钢管内部注入，经桩底出浆孔从桩底位置沿钢管外侧返流至桩顶设计标高；③ 将注浆管缓慢拔出，并将钢管内填满水泥砂浆，再对钢管外侧进行补浆。此时钢管内、外两侧完全被水泥砂浆包裹，达到设计强度后施工完毕。

该微型钢管桩成桩工艺对施工空间要求较低，且可以避免钢管与土体直接接触，有效提高桩体防腐性能与桩侧摩阻力，很好地满足了建筑基础托换工程的需求。然而，在黄土高填方场地，当微型钢管桩穿越较厚填土层且填土填筑不密实时，桩体具有极大的长细比，容易发生屈曲破坏。另外，在增大正摩阻力的同时，因桩侧土体沉降产生的负摩阻力也要显著大于普通微型钢管桩，对桩体屈曲稳定性不利。因此，需对该桩型在黄土高填方地基中的屈曲特性进行研究。

1.2   微型钢管桩屈曲特性分析

微型钢管桩由于施工误差存在初弯曲与初偏心，且材料存在不均匀性。在桩顶轴心荷载作用下，桩体除了发生轴向压缩变形，还会发生附加弯曲变形。随着轴心荷载增加，桩体弯曲变形逐渐加剧，当超过桩体与桩侧土体抵抗弯曲的变形能力时，桩体会发生突然的屈曲破坏，其失稳类型与无侧向约束的压杆相同。对压杆的轴心受压屈曲临界荷载计算时，通常将压杆抽象为弹性、均质且轴向压力与桩体轴线重合的“理想轴心受压直杆”，再利用施加在压杆上假想的微小横向力代替初弯曲与材料不均匀性的影响，使压杆产生弯曲变形。当轴向力不大时，撤去横向力压杆轴线将恢复为原来的直线平衡形态，压杆保持稳定；当轴向力增大到界限值时，撤去横向力桩体轴线将保持弯曲平衡形态，此时压杆处于临界屈曲状态，压杆端部轴向荷载即为屈曲临界荷载。

微型钢管桩一般与建筑筏板或承台相连，桩体全部埋入土层中。但对于黄土高填方场地，施工完毕后，后续使用过程中，地基仍可能产生湿陷变形或填筑土体蠕变变形，导致建筑局部筏板或承台下产生空穴，使得微型钢管桩桩顶裸露于土层之上，缺少土体约束作用。因此，需考虑桩顶自由段对其屈曲稳定性的影响。

另外，在考虑桩侧土体约束作用时，由于微型钢管桩刚度较小，与大直径基桩相比，荷载作用下桩体屈曲时挠曲线斜率更大，相应的桩侧土体水平变形的变化率较大，使得桩侧土体受力连续性，即桩侧土体间的相互剪切作用对微型钢管桩屈曲特性的影响进一步增强。

因此，本文以压杆的轴心受压屈曲临界荷载计算方法为基础，考虑桩侧土体受力变形连续性对土体水平抗力的贡献，计算桩侧土体约束作用下的微型钢管桩屈曲临界荷载，并讨论桩侧负摩阻力的影响。

1.3   基本假设

1)微型钢管桩为均质弹性体，且轴线为直线，桩顶轴向荷载与轴线重合；

2)桩土接触紧密，无空隙，桩土协调变形；

3)正摩阻力对屈曲临界荷载影响较小^{[10 − 12]}，且有利，故忽略正摩阻力的影响；

4)钢管外侧水泥砂浆保护层施工质量难以保证，且受弯易开裂，故不考虑其抗弯刚度。

1.4   计算模型的建立

当轴心受压微型钢管桩处于屈曲临界状态时，桩身保持弯曲形态。微型钢管桩刚度较小，在土体水平抗力作用下，桩身挠曲线为多个半波曲线^[17]，且最大横向位移发生在桩体上半段^[22]。此时，桩顶承受轴心荷载F_cr，桩顶自由段无侧向约束，桩体嵌固端按中性点a位置分为2个部分，中性点以上桩体受到桩侧土体的水平抗力p_k与负摩阻力${\tau _{\text{s}}}$作用，中性点以下桩体仅受桩侧土体的水平抗力p_k作用。中性点位置根据文献[23]确定。在黄土高填方场地，要求微型桩桩底嵌入坚硬持力层，桩底可视为固定端。对于桩顶边界条件，当采用锚杆静压方式施工时，微型钢管桩需穿透建筑筏板或承台，桩顶利用法兰盘或其他可靠措施与筏板或承台顶面相连，此时桩顶可视为固定端；当采用坑式静压方法施工时，微型钢管桩桩顶仅通过简单植筋与筏板或承台底面相连，此时桩顶可视为铰接。计算模型如图2所示，L₁为自由段长度(m)；L₂为受负摩阻力作用的嵌固段长度(m)；L₃为不受负摩阻力作用的嵌固段长度(m)。

图  2  轴心荷载下微型钢管桩屈曲临界荷载计算简图

Figure  2.  Calculation diagram the critical load for buckling of the micro steel pipe piles under axial load

下载: 全尺寸图片 幻灯片

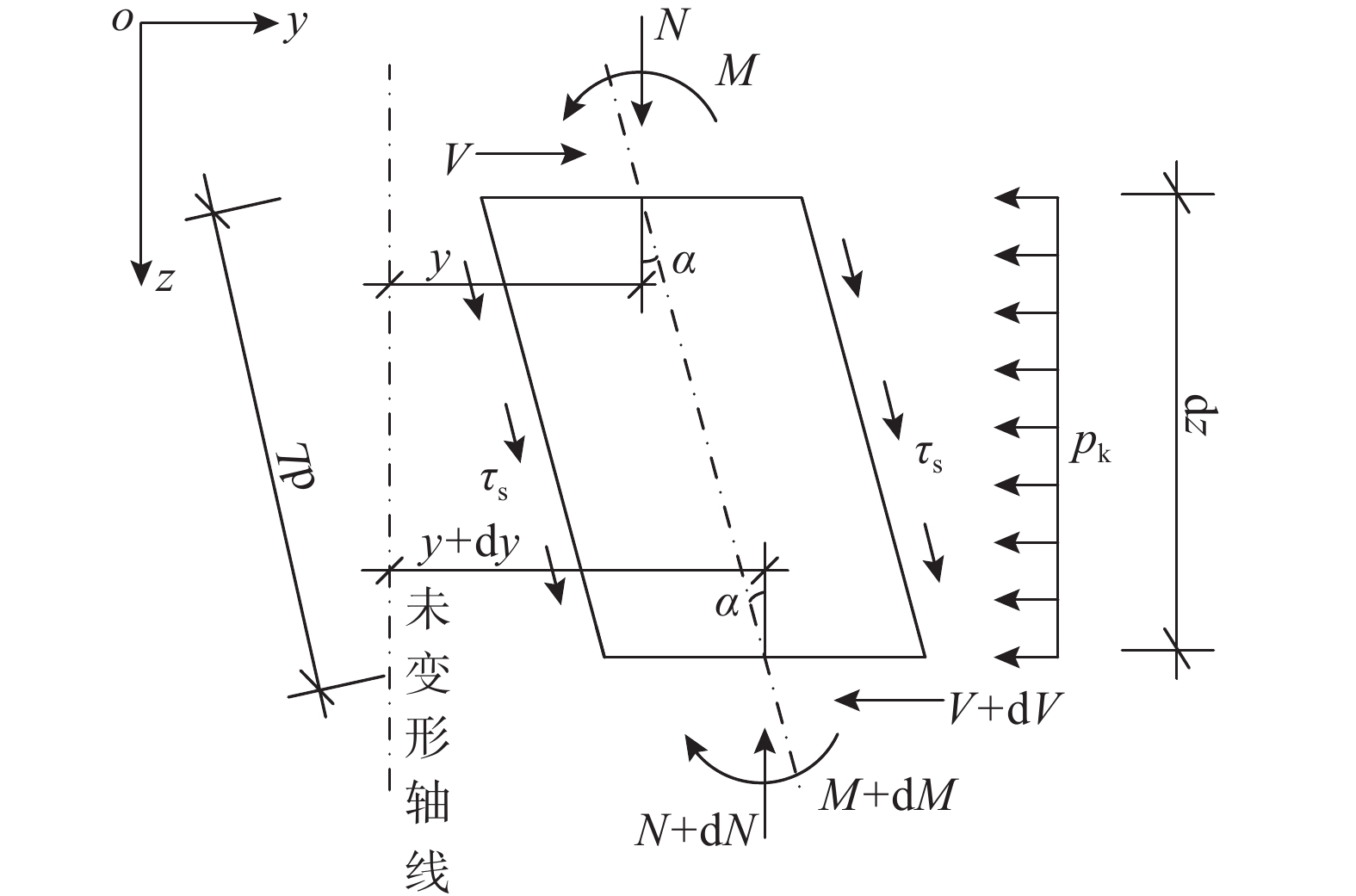
1.5   微分方程的建立

首先，对受负摩阻力作用的嵌固段进行分析，其某微元段受力分析如图3所示。y为桩体轴线的水平位移(m)，以向右为正；$\alpha$为变形后桩体轴线与z轴的夹角，以逆时针转动为正；N为桩体轴力(kN)，以受压为正；V为截面剪力(kN)，以顺时针转动为正；M为截面弯矩(kN·m)，以左侧受拉为正。该微元段长度为dL，沿z轴投影长度为dz。特别指出：在微元段受力分析时，根据压杆屈曲机理，需考虑轴力引起的二阶效应，即考虑夹角$\alpha$的影响，则${\text{d}}L = {\text{d}}{\textit{z}}/\cos \alpha$；当建立桩体微分方程后，式中${\textit{z}} = L(\cos \alpha )$，与夹角$\alpha$的余弦值相关，计算复杂，由于桩体变形属于为弹性小变形，桩身轴线与z轴的夹角$\alpha$较小，可取$\cos \alpha \approx 1$，此时z=L，仅使桩长略微增大，不影响屈曲分析。

图  3  桩体微元段受力分析

Figure  3.  Force analysis of differential section of pile

下载: 全尺寸图片 幻灯片

对该微元段受力分析，负摩阻力${\tau _{\rm{s}}}$采用文献[23]推荐的方法计算。

式中：${\xi _n}$为负摩阻力系数；$\sigma '$为z深度处土体的竖向有效应力；$\gamma$为土体重度，地下水位以下取浮重度。

由$\sum {{F_{\text{z}}}} {\text{ = }}0$得：

式中；d为桩径(m)。

由$\sum {{F_y}} = 0$得：

式中：${b_0}$/m为桩身计算宽度；$\tan \alpha = {\text{d}}y/{\text{d}}{\textit{z}}$。

由$\sum M = 0$得：

将式(4)对z求一阶导，得：

将式(1)、式(3)代入式(5)得：

由材料力学公式$M = EIy''$得：

式中，EI为微型钢管桩的弹性受弯刚度，可根据下式计算^[24]：

式中：${E_{{\text{scm}}}}$、${I_{{\text{sc}}}}$为钢管混凝土构件弹性受弯模量(kPa)与截面惯性矩(m⁴)；${E_{\rm{sc}}}$为钢管混凝土构件的弹性模量(kPa)；${k_E}$为钢管混凝土轴压弹性模量换算系数；${f_{\rm{sc}}}$为钢管混凝土抗压强度设计值(kPa)；${\alpha _{\rm{sc}}}$为钢管混凝土构件的含钢率；${E_{\rm{c}}}$、${E_{\rm{s}}}$为钢材与混凝土的弹性模量(kPa)；${I_{\rm{s}}}$、${I_{\rm{c}}}$为钢管与混凝土部分的惯性矩(m⁴)。

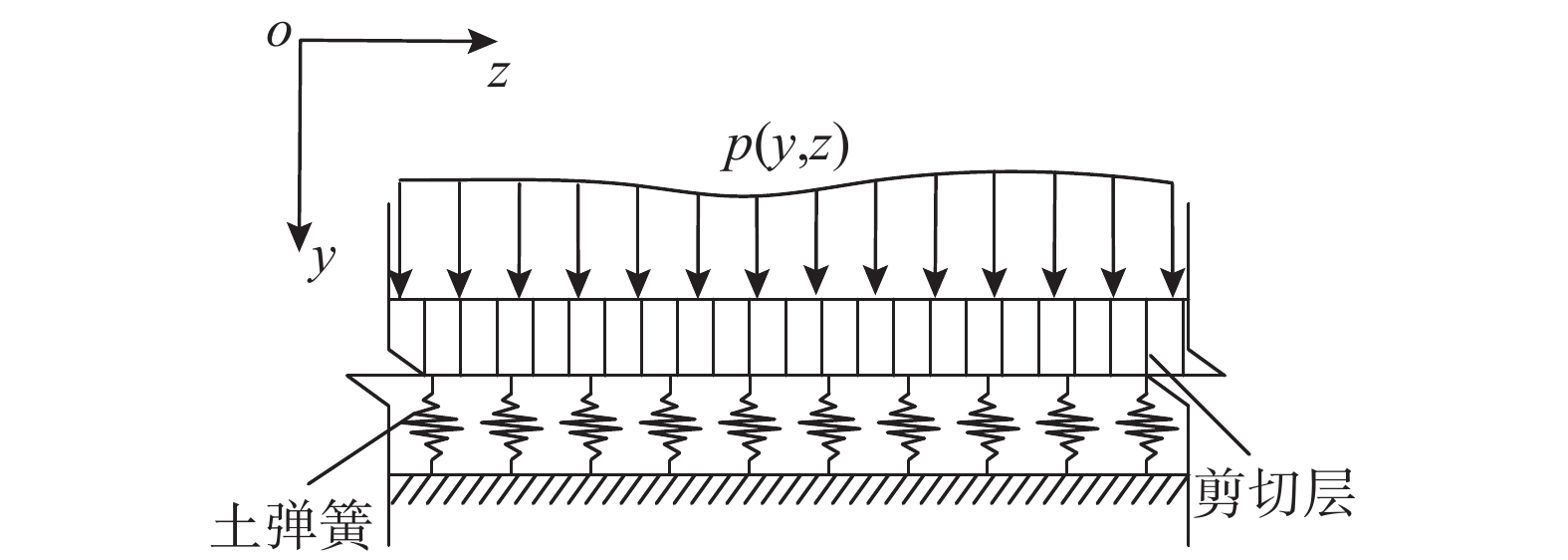
目前，考虑桩侧土体受力变形连续性的地基梁模型中最常用的为Pasternak双参数模型^{[25 − 26]}。该模型以Winkler单参数弹性地基梁模型为基础，在离散弹簧单元上设置一层可产生剪切变形而不可压缩的剪切层，反映受力土体间的剪切作用，从而考虑土体受力变形的连续性，如图4所示。

图  4  Pasternak双参数地基梁模型

Figure  4.  Pasternak double-parameter foundation model

下载: 全尺寸图片 幻灯片

Pasternak双参数地基梁模型地基反力为：

式中：k为桩侧土的水平抗力系数(kN/m³)，可采用c法计算，$k = c{( {\textit{z}} - {L_1})^{0.5}}$，c为地基水平抗力系数的比例系数(kN/m^3.5)，可根据表1取值；${G_{\rm p}}$为剪切层的剪切模量(kPa)，可采用Tanahashi^[27]提出的经验公式计算：

式中：E_s为土体弹性模量(kPa)；ν为土体泊松比；t为剪切层厚度(m)，可近似取11d ^[28]。

表  1  地基水平抗力系数的比例系数c值^[29]

Table  1.  The scale coefficient c value of the horizontal resistance coefficient of the foundation

序号	地基土类型	c/(MN/m3.5)
1	${I_{\text{L}}} {\geqslant} 1$的流塑性黏性土	4~8
2	$1 > {I_{\text{L}}} {\geqslant} 0.5$的软塑性黏土，粉砂	8~15
3	$0.5 > {I_{\text{L}}} {\geqslant} 0$的硬塑性粘性土，细砂，中砂	15~30
4	半干硬性粘性土、粗砂	30~50
5	砾砂、角砾砂、砾石土、碎石土、卵石土	50~80
6	块石土、漂石夹砂土	80~120

下载: 导出CSV 

| 显示表格

将式(2)、式(8)代入式(7)，得：

式中，${T_{\rm s}}$为深度z以上桩体受到的负摩阻力之和，${T_{\rm s}} = {\xi _n}\gamma {( {\textit{z}} - {L_1})^2}\pi d/2$。

式(9)即为轴心荷载下微型钢管桩受负摩阻力作用的嵌固段的平衡微分方程。同理可得桩体自由段、不受负摩阻力作用的嵌固端的平衡微分方程为：

式中，${T_{\rm e}}$为中性点以上桩体受到的负摩阻力之和，${T_{\rm e}} = {\xi _n}\gamma {L_2}^2\pi d/2$。

1.6   屈曲临界荷载的求解

上述建立的微分方程中包含4阶变系数微分方程，故采用有限差分法求解。

1.6.1   差分方程的建立

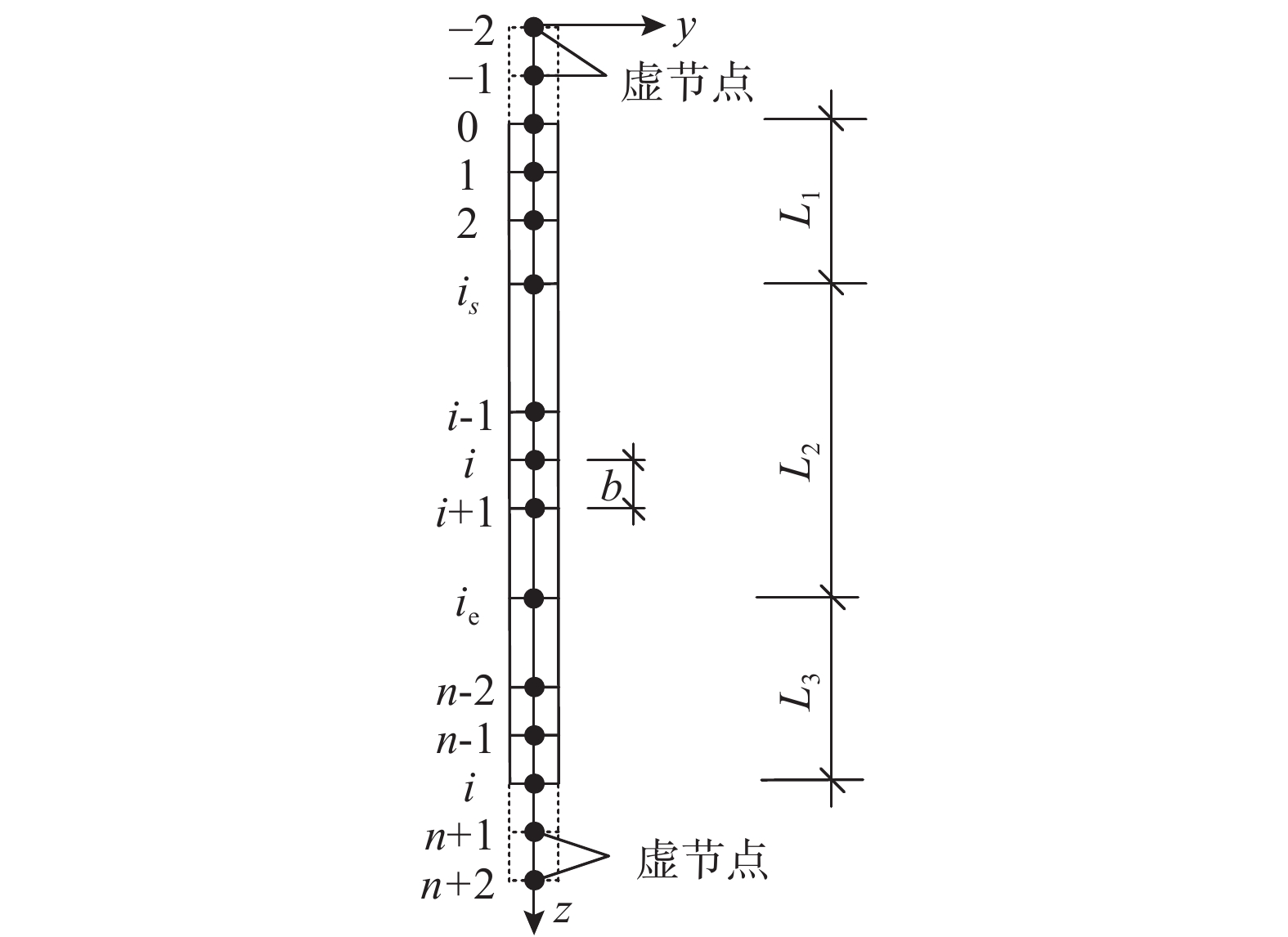
将微型钢管桩沿长度方向划分为n个单元，分段长度为b，并在桩顶与桩底各增设2个虚单元，划分过程中使地面处、土体分层处及中性点处拥有节点。记i节点处，桩体水平位移、截面轴力、弯矩、剪力为y_i、N_i、M_i、V_i，对于受负摩阻力作用的嵌固段，该节点以上负摩阻力之和为T_s,i，对于不受负摩阻力作用的嵌固段，该节点以上负摩阻力之和为T_e,i；i_s为地面处的桩体节点，${i_{\rm{s}}} = {L_1}/b$，i_e为中性点处的桩节节点，${i_{\rm{e}}} = ({L_1} + {L_2})/b$，如图5所示。

图  5  有限差分法计算简图

Figure  5.  Calculation diagram of finite difference method

下载: 全尺寸图片 幻灯片

一维中心差分公式为：

式(9)中深度z以上桩体受到的负摩阻力之和${T_{\rm{s}}}$为连续函数，但实际工程中往往存在多种土层，需分段考虑。根据有限差分法的离散化方式，将负摩阻力${\tau _{\rm{s}}}$按照分段长度b离散处理，深度z_i对应的分层土体所产生的负摩阻力之和为：

将深度z_i以上土体所产生的负摩阻力叠加，可以得到深度z_i以上负摩阻力之和为：

将式(12)、式(13)代入式(9)~式(11)，得：

式中：

1.6.2   边界条件

桩体每个实节点均能写出上述线性方程式，共n+1个方程、n+5个未知水平位移，需考虑桩顶与桩底边界条件作为补充方程。

1) 桩顶边界条件

微型钢管桩桩顶与建筑筏板或承台的连接形式主要有铰接与刚接两种，其边界条件表达式为：

根据材料力学公式：

将式(12)、式(19)代入式(17)、式(18)，得：

2)桩底边界条件

微型钢管桩桩底需嵌入风化岩层，可视为固定端，其边界条件表达式为：

将式(12)、式(19)代入式(22)，得：

1.6.3   屈曲临界荷载的求解

当桩体处于屈曲临界状态时，桩身将保持弯曲形态，水平位移应不全为0。因此，桩体水平位移非零解对应的桩顶荷载最小值即为屈曲临界荷载。

当桩顶边界条件为铰接时，由式(14)~式(16)、式(20)、式(23)组成的线性方程组共n+5个方程，n+5个未知水平位移，其矩阵形式为：

式中：${\boldsymbol{y}} = \left\{ {{y_{ - 2}},{y_{ - 1}},{y_0}, \cdots ,{y_{i - 1}},{y_i},{y_{i + 1}}, \cdots ,{y_n},{y_{n + 1}},{y_{n + 2}}} \right\}$，

当式(24)存在非零解时，其系数矩阵的行列式应等于0：

将式(25)展开可得到F_cr的n+1次方程，求解得到的最小根F_cr,min即为微型钢管桩的屈曲临界荷载。

当桩顶边界条件为刚接时，可由式(14)~式(16)、式(21)、式(23)组成线性方程组。同理，可根据该方程组系数矩阵行列式为0，求解其最小根，得到微型钢管桩的屈曲临界荷载。

2   试验验证

2.1   室内模型试验

文献[30]开展了微型桩竖向荷载下单桩承载力室内模型试验。微型桩桩径为30 mm，桩长为1.5 m，用有机玻璃制作，弹性模量为$2.0 \times {10^3}$ MPa，桩身用环氧树脂固化剂均匀粘贴细砂，模拟桩侧粗糙度。为方便桩顶加载，以及避免桩端土体发生局部剪切破坏，微型桩桩顶和桩底均设置有承台，桩体嵌入承台30 mm。模型箱底部填筑碎石土作为持力层，上部填筑饱和黄土，如图6所示。土体物理参数见表2。加载制度为慢速维持荷载法。

图  6  试验示意图　/mm

Figure  6.  Schematic diagram of the test

下载: 全尺寸图片 幻灯片

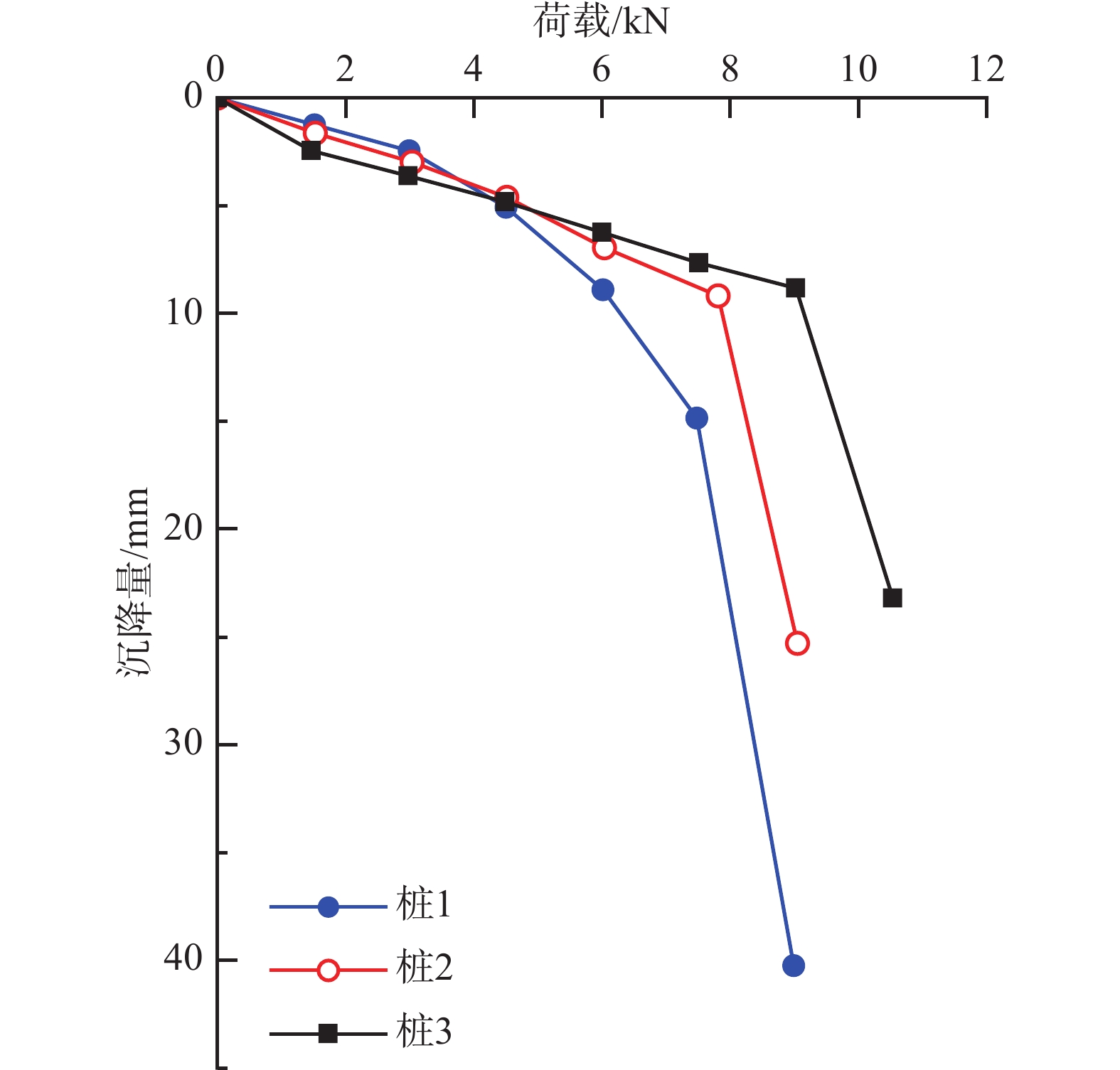
表  2  土体物理参数

Table  2.  Physical parameters of soil

	含水率/(%)	塑限/(%)	液限/(%)	弹性模量Es/MPa	泊松比v
黄土	30.80	14.50	30.80	2.0	0.42

下载: 导出CSV 

| 显示表格

试验得到的桩顶荷载-沉降(Q-s)曲线见图7。三次试验所得Q-s曲线均为陡降型，且经验算桩端土体发生局部剪切破坏时桩顶荷载值至少需大于130 kN，可以判定桩体发生了屈曲破坏，桩顶沉降陡增点处的荷载为屈曲临界荷载。

图  7  桩顶荷载-沉降(Q-s)曲线

Figure  7.  Load-settlement (Q-s) curve of pile top

下载: 全尺寸图片 幻灯片

文献[30]中饱和黄土层c值取4 MN/m^3.5，k值取5 MN/m³，桩体抗弯刚度EI=0.0795 ${\text{kN}} \cdot {{\text{m}}^{\text{2}}}$，桩顶与桩底均视为固定端。利用该参数对试验中桩体的屈曲临界荷载进行计算，考虑到土体为饱和状态填筑，且经过分层压实，对桩体基本不产生负摩阻力，故不考虑负摩阻力的影响。本文方法、文献[30]方法、文献[31]方法及文献[30]试验得到的屈曲临界荷载见表3。

表  3  屈曲临界荷载

Table  3.  The buckling critical load /kN

试验结果[30]					理论计算结果
桩1	桩2	桩3	平均值		文献[30]方法	文献[31]方法	本文方法
7.90	8.00	8.40	8.10		8.05	7.05	8.69

下载: 导出CSV 

| 显示表格

由表3可以看出，文献[31]方法得到的屈曲临界荷载与试验结果、本文计算方法结果的误差分别为13.0%、12.4%，而本文方法计算得到的屈曲临界荷载与文献[30]的试验、理论计算结果更为接近，误差分别为7.28%，8.0%，误差较小，可以一定程度说明本文方法的正确性。另外，文献[30]的理论方法仅适用于桩体全部嵌入土层、且桩周为均质土层的情况，而本文方法能够应用于复杂土层、且桩顶存在自由段的屈曲临界荷载计算。因此，与文献[30]的理论方法相比，本文方法应用工况更为广泛。

2.2   现场试验

兰州某住宅楼地基土为自重湿陷性黄土，因管道漏水，导致地基产生不均匀沉降，采用坑式静压钢管桩托换处理。钢管直径为168 mm，壁厚6.5 mm，屈服强度为400 MPa，弹性模量为$2.06 \times {10^5}$ MPa，每节长度为1 m，通过钢管自带螺纹连接。桩长24 m，桩底嵌入风化岩层。5 m深度范围内桩周土体为饱和湿陷性黄土层，弹性模量E_s为5 MPa，泊松比v为0.36；其余深度为非饱和湿陷性黄土层，弹性模量E_s为9 MPa，泊松比v为0.33。

为测试微型钢管桩的屈曲临界荷载，通过楼体底板提供反力，对未注浆的空心钢管桩施加轴向荷载。微型钢管桩桩顶1.5 m范围内裸露于土层之上，土层深度约0.5 m范围内桩体与土体间存在间隙，可视桩顶自由段长度L₁为2 m。加载过程中，桩顶荷载达到1800 kN后陡降至1600 kN，并维持稳定。卸载后，钢管桩有明显的回弹现象，桩顶回弹量为8 cm，明显超过钢管桩弹性变形导致的桩顶沉降量。因此，可以判定钢管桩发生了屈曲破坏，屈曲临界荷载为1800 kN。

利用本文方法对该试验进行计算，桩顶受楼体底板约束，可视为铰接，桩底嵌入风化岩层，可视为固定端。根据表1选取桩侧土体水平抗力系数的比例系数c值，考虑到桩体水平位移较大，c值应适当降低，故选取饱和黄土层与非饱和黄土层地基c值分别为4.0 MN/m^3.5、8.0 MN/m^3.5；另外，微型钢管桩桩底达到设计深度后即刻加载，还未受到桩侧负摩阻力作用，计算时，与实际情况一致，不考虑负摩阻力作用。将钢管桩沿桩长划分为48个单元，分段长度b=0.5 m，计算得到桩体屈曲临界荷载为1743.5 kN，与试验结果误差较小，一定程度上验证了本文方法的正确性。

3   工程实例分析

3.1   工程概况

兰州市某小区两栋高层住宅楼发生倾斜，该场地为黄土高填方区，故采用高压注浆微型钢管桩进行基础托换处理。为确定微型钢管桩的极限承载力，需进行现场单桩竖向静载试验。试验加载采用压重平台反力装置，如图8所示，加载制度为慢速维持荷载法。土层与微型钢管桩参数见表4、表5。

图  8  微型钢管桩单桩竖向静载试验

Figure  8.  Test of vertical static load of single pile of micro steel pipe pile

下载: 全尺寸图片 幻灯片

表  4  土层物理参数

Table  4.  Physical parameters of soil

土层	厚度/ m	重度$\gamma$/ (kN/m3)	粘聚力 c/kPa	内摩擦角 $\varphi$/(°)	弹性模量 Es/MPa	泊松比 v
粉土(回填土)	3.5	18.1	6	11.0	3.5	0.36
饱和粉土(回填土)	25.7	18.8	10	13.5	4.5	0.35
砂岩	4.2	19.7	28	30.0	25.0	0.25

下载: 导出CSV 

| 显示表格

表  5  微型钢管桩物理参数

Table  5.  Physical parameters of micro steel pipe pile

桩径/m	桩长/m	钢管			混凝土弹性模量 Ec/MPa
		直径/m	壁厚/mm	弹性模量Es/MPa
0.198	33	0.168	8	$2.06 \times {10^5}$	$2.95 \times {10^4}$

下载: 导出CSV 

| 显示表格

3.2   本文计算模型

选取桩侧土体水平抗力系数的比例系数c值时，考虑到桩体水平位移较大，且桩周土层均为填土，c值应将其适当降低，故根据表1选取粉土层与饱和粉土层c值依次为3.0 MN/m^3.5，4.0 MN/m^3.5。桩顶自由段长度L₁=0 m，填土层下即为风化岩层，根据文献[23]确定中性点深度为29.2 m，即桩体受负摩阻力作用的嵌固端长度L₂=29.2 m。对桩体抗弯刚度EI计算时，钢管混凝土轴压弹性模量换算系数${k_E}$取626.9，钢管混凝土构件的含钢率${\alpha _{\rm sc}}$为10.25%，钢管混凝土抗压强度设计值${f_{\rm{sc}}}$为55.5 MPa，钢管与混凝土部分的惯性矩${I_{\rm s}}$、${I_{\rm c}}$分别为$6.933 \times {10^{ - 6}}$ m⁴、$3.217 \times {10^{ - 5}}$ m⁴，计算得到桩体抗弯刚度EI为1771.4 ${\text{kN}} \cdot {{\text{m}}^{\text{2}}}$。

砂岩水平抗力极高，可视饱和粉土层与砂岩界面处即为桩底固定端；桩顶处受压重平台约束，可视为铰接。利用上述建立的计算方法对该试验中的微型钢管桩屈曲临界荷载进行计算，将微型钢管桩沿桩长划分为73个单元，分段长度为b=0.4 m。计算得到桩体屈曲临界荷载为4114.1 kN。

3.3   数值模拟

采用ABAQUS有限元软件对该实例进行三维数值模拟，将微型钢管桩简化为均质弹性体，土体与微型钢管桩均采用8节点实体单元，土体本构采用Mohr-Coulomb模型，桩土接触面法向采用“硬”接触，切向采用摩擦接触。模型尺寸及计算结果如图9所示。

图  9  有限元模型尺寸与计算结果　/m

Figure  9.  The dimensions of the finite element model and its calculation results

下载: 全尺寸图片 幻灯片

将本文方法、文献[31]方法及数值模拟的结果对比分析。按照选取c值时的降低程度，粉土层与饱和粉土层k值依次取为3.75 MN/m³、5 MN/m³，计算结果见表6。本文计算方法与数值模拟的结果更为接近，误差为3.70%，而文献[31]方法误差较大，为17.1%，其原因为该方法利用Winkler弹性地基梁法考虑桩侧土抗力，将桩侧土体简化为离散弹簧，未考虑相邻土体间的剪切作用，其结果与本文方法中不考虑桩侧土剪切作用计算结果相近，误差为5.0%。另外，在该工况下，考虑桩侧土剪切作用使屈曲临界荷载提升了10.4%，影响较大，而负摩阻力仅使屈曲临界荷载略微降低。

表  6  两种方法与数值模拟得到的屈曲临界荷载

Table  6.  The critical loads of buckling obtained by the two methods and numerical simulations /kN

本文计算方法			数值模拟	文献[31]
考虑桩侧土剪切作用 与负摩阻力	不考虑桩侧土 剪切作用	不考虑 负摩阻力
4114.1	3725.6	4120.6	4272.0	3540.7

下载: 导出CSV 

| 显示表格

对微型钢管桩处于屈曲临界状态时的桩身挠曲线进行分析。在轴心荷载作用下，只能得到挠曲线的形状，其具体水平位移无法确定，故规定挠曲线的最大水平位移为$\delta$，桩身挠曲线如图10所示。三种方法得到的挠曲线的极值均随深度的增加逐渐减小，减小速率从大到小依次为本文方法、数值模拟、文献[31]方法。三种方法得到的桩身挠曲线均表现出：桩体上半段的水平位移远远大于其余部分，尤其是从地面到桩身挠曲线第二个拐点之间桩体水平位移明显较大。可以得出，桩体的屈曲临界荷载主要由桩体上半段决定，从地面到桩身挠曲线第二个拐点之间的影响尤为重要。

图  10  屈曲临界荷载下的桩身挠曲线

Figure  10.  The deflection line of the pile under the critical loads of buckling

下载: 全尺寸图片 幻灯片

对三种方法得到桩体上半段桩身挠曲线对比分析，对于桩身最大正水平位移，三种方法得到的深度均为1.6 m；对于桩身最大负水平位移，本文方法与数值模拟的结果分别为−0.291$\delta$、−0.330$\delta$，误差为11.8%，而文献[31]方法结果为−0.576$\delta$，误差较大，并且三者深度分别为4.4 m、4.2 m、4.8 m，本文方法与数值模拟结果更为接近。因此可以说明，从地面到桩身挠曲线第二个拐点之间，本文方法得到的桩身挠曲线与数值模拟结果更为接近。

在10 m以下深度范围内，三种方法得到的桩身水平位移差别较大，这是桩侧土水平抗力系数计算方法的局限性导致的。常数法和c法中的土体水平抗力系数的参数，均是根据现场桩基水平静载试验的荷载-位移曲线得到的，首先选取试验中桩体地面处水平位移为一定值时的桩顶荷载值，然后不断假定土体水平抗力系数的参数，并按照弹性桩方法计算桩体水平位移，直至桩体地面处水平位移为该定值为止，即得到了该工况下土体水平抗力系数的参数^[32]。可见，在土体水平抗力系数的参数确定过程中，并没有考虑深层处桩体的水平位移是否符合实际情况。本文采用c法计算桩侧土体水平抗力系数k，其假设k值随深度的增加呈抛物线增大，深度越大，桩侧土体水平抗力系数k越大，桩侧土体水平约束作用越强，使得桩体下半段水平位移小于数值模拟的结果；而文献[31]方法采用常数法，假设地基水平抗力系数沿深度不变，使得桩体下半段水平约束作用较弱，桩体下半段水平位移大于数值模拟的结果。

综上所述，两者计算得到的深层处桩身挠曲线均与数值模拟存在一定差距，但本文方法得到的挠曲线在桩顶以下一定深度范围内与数值模拟结果更为接近。结合微型钢管桩的屈曲临界荷载由桩体上半段决定的性质，可以反映出，本文方法对微型钢管桩屈曲分析更为适用。

3.4   参数分析

为了进一步明确微型钢管桩的屈曲特性，以上述工程实例为基础，分析桩侧土抗力、负摩阻力、桩体刚度及桩顶自由段长度对微型钢管桩屈曲临界荷载的影响。

3.4.1   桩侧土抗力

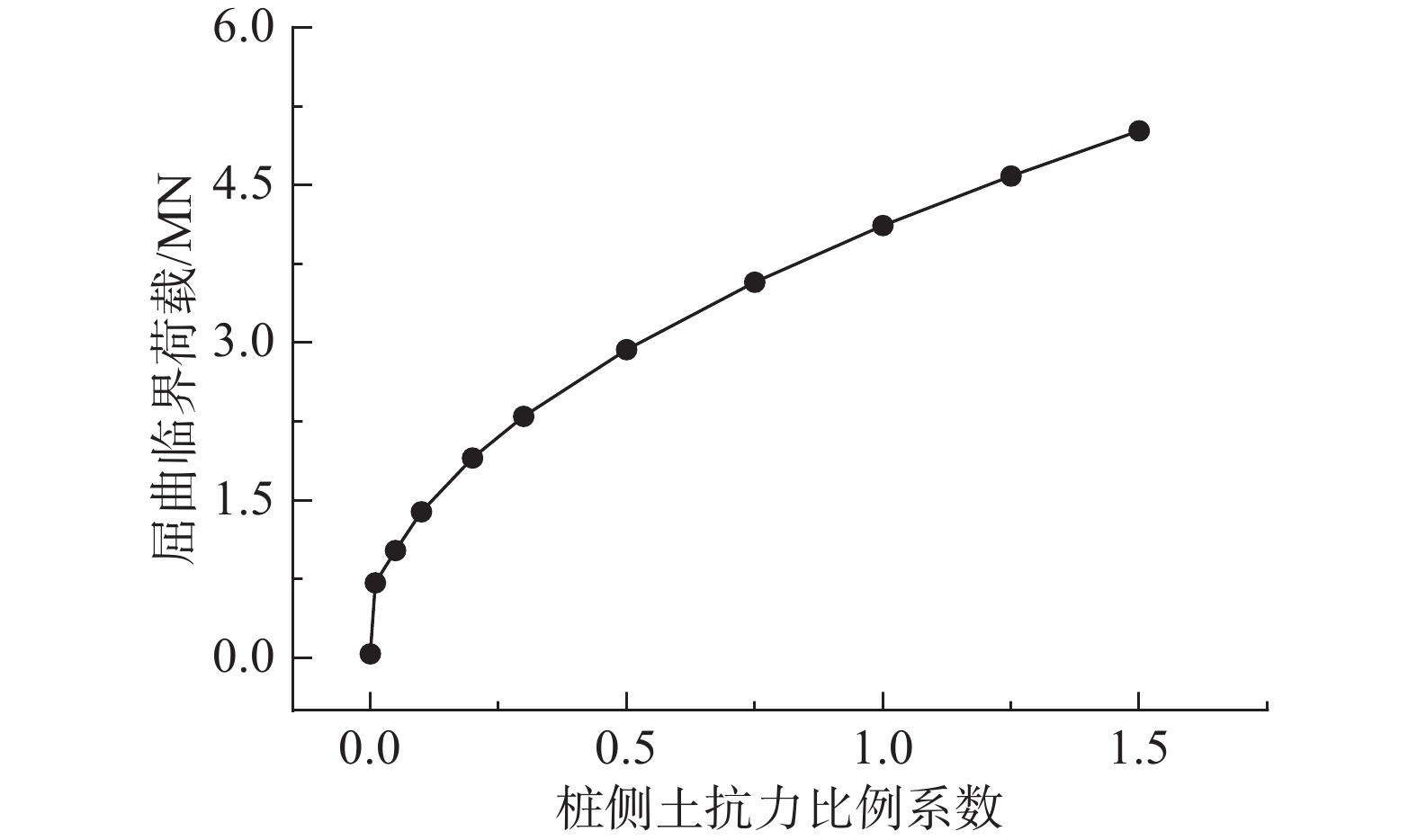
桩侧土抗力计算主要由桩侧土水平抗力系数的比例系数c及土体剪切刚度G_p决定的。以上述工程实例中的参数为基准，按0~1.5的比例计算这两个参数，考虑不同桩侧土抗力对微型钢管桩屈曲临界荷载的影响，如图11~图12所示。

图  11  不同桩侧土抗力下的屈曲临界荷载

Figure  11.  Buckling critical loads under different soil resistance at pile side

下载: 全尺寸图片 幻灯片

图  12  不同桩侧土抗力下的桩身挠曲线

Figure  12.  The deflection line of the pile under different pile side soil resistance

下载: 全尺寸图片 幻灯片

由图11可知，随着桩侧土抗力的增加，微型钢管桩的屈曲临界荷载呈非线性增长。当桩侧土抗力比例系数为0.5与1.5时，屈曲临界荷载分别减小了28.6%与增大了22.0%，可见，桩侧土抗力对屈曲临界荷载影响较大。另外，当桩侧土抗力比例系数为0时，即不受桩侧土的约束作用时，桩体屈曲临界荷载为41.9 kN，与欧拉公式计算结果一致。

由图12可知，随着桩侧土抗力的增加，桩身挠曲线逐渐变得复杂。当桩侧土抗力的比例系数为0时，桩身挠曲线近似正弦曲线，存在一个拐点；随着桩侧土抗力的增大，拐点数逐渐增多，不再是简单的正弦或余弦曲线，且桩身上半段水平位移与其余部分的差距逐渐增大，桩体屈曲类型由整体屈曲向桩身上半段屈曲过渡。这表明，桩身挠曲线与桩侧土抗力显著相关，若采用假设桩身挠曲线的方法求解屈曲临界荷载，必须考虑桩侧土抗力对桩身挠曲线的影响。

3.4.2   负摩阻力

在其他条件不变的情况下，以上述工程实例为基础，分析不同桩侧土抗力下不同程度的负摩阻力对桩体屈曲临界荷载的降低程度。桩侧土抗力降低系数按0.25、0.5、1.0的比例取值，负摩阻力按0~4的比例取值。计算结果见表7。从表中可以看出，随着负摩阻力的增大，桩体屈曲临界荷载的降低程度逐渐增大，且当桩侧土抗力越小时，负摩阻力的影响程度相对越明显。

表  7  不同土抗力下负摩阻力对屈曲临界荷载的降低程度

Table  7.  The reduction degree of negative friction to buckling critical load under different soil resistance

桩侧土抗力降低系数	负摩阻力比例系数/(%)
	1	2	3	4
0.25	0.60	1.23	1.90	2.60
0.50	0.31	0.62	0.95	1.28
1.00	0.16	0.32	0.48	0.65

下载: 导出CSV 

| 显示表格

为了进一步分析不同桩侧土抗力下，负摩阻力对桩体屈曲临界荷载的影响机理。选取中性点深度分别为4 m、8 m、12 m及桩底处，改变负摩阻力的作用长度，计算相应的屈曲临界荷载，计算结果见表8。从表中可以看出，不同桩侧土抗力下，当中性点由第一拐点深度附近增加到第二拐点深度附近时，负摩阻力对桩体屈曲临界荷载的影响程度相对有较大的增加，而当中性点深度大于第二拐点深度后，随着中性点深度的增加，负摩阻力对桩体屈曲临界荷载的影响程度基本不变；并且，当桩侧土抗力较小时，第二拐点深度相对较大，负摩阻力对屈曲临界荷载的影响也相对较大。因此，负摩阻力对桩体屈曲的影响主要作用在第二拐点以上深度，从而可以解释，桩侧土抗力越小，负摩阻力的影响程度相对越明显的现象，同时也证明了，桩体屈曲属于桩体上半段的局部屈曲破坏。

表  8  不同中性点深度负摩阻力对屈曲临界荷载的降低程度

Table  8.  The reduction of critical buckling load by negative friction resistance at different neutral point depths

桩侧土抗力 降低系数	拐点深度/m	中性点 深度/m	负摩阻力比例系数/(%)
			1	2	3	4
0.25	第一拐点：4.54 第二拐点：8.42	4	0.27	0.54	0.81	1.09
		8	0.54	1.09	1.65	2.24
		12	0.59	1.22	1.86	2.55
		全长	0.60	1.23	1.90	2.60
0.5	第一拐点：3.93 第二拐点：7.27	4	0.14	0.29	0.44	0.59
		8	0.29	0.59	0.89	1.20
		12	0.31	0.62	0.94	1.28
		全长	0.31	0.62	0.95	1.28
1.0	第一拐点：3.34 第二拐点：6.21	4	0.11	0.21	0.32	0.43
		8	0.16	0.32	0.48	0.64
		12	0.16	0.32	0.48	0.64
		全长	0.16	0.32	0.48	0.65

下载: 导出CSV 

| 显示表格

对上述不同工况下负摩阻力对桩体屈曲临界荷载的影响程度进行统计发现，负摩阻力对桩体屈曲临界荷载的降低程度均未超过3%。其原因为：负摩阻力对桩体屈曲的影响主要作用在第二拐点以上深度，作用长度较短，且负摩阻力的大小与土体自重相关，深度较小时，负摩阻力有限，因此其对桩体屈曲临界荷载的影响相应较小。另外，微型钢管桩侧面积较小，使负摩阻力作用面相应较小，进一步减小了负摩阻力对屈曲临界荷载的影响。基于以上分析，为简化计算，可忽略负摩阻力对屈曲临界荷载的影响。

3.4.3   桩体刚度

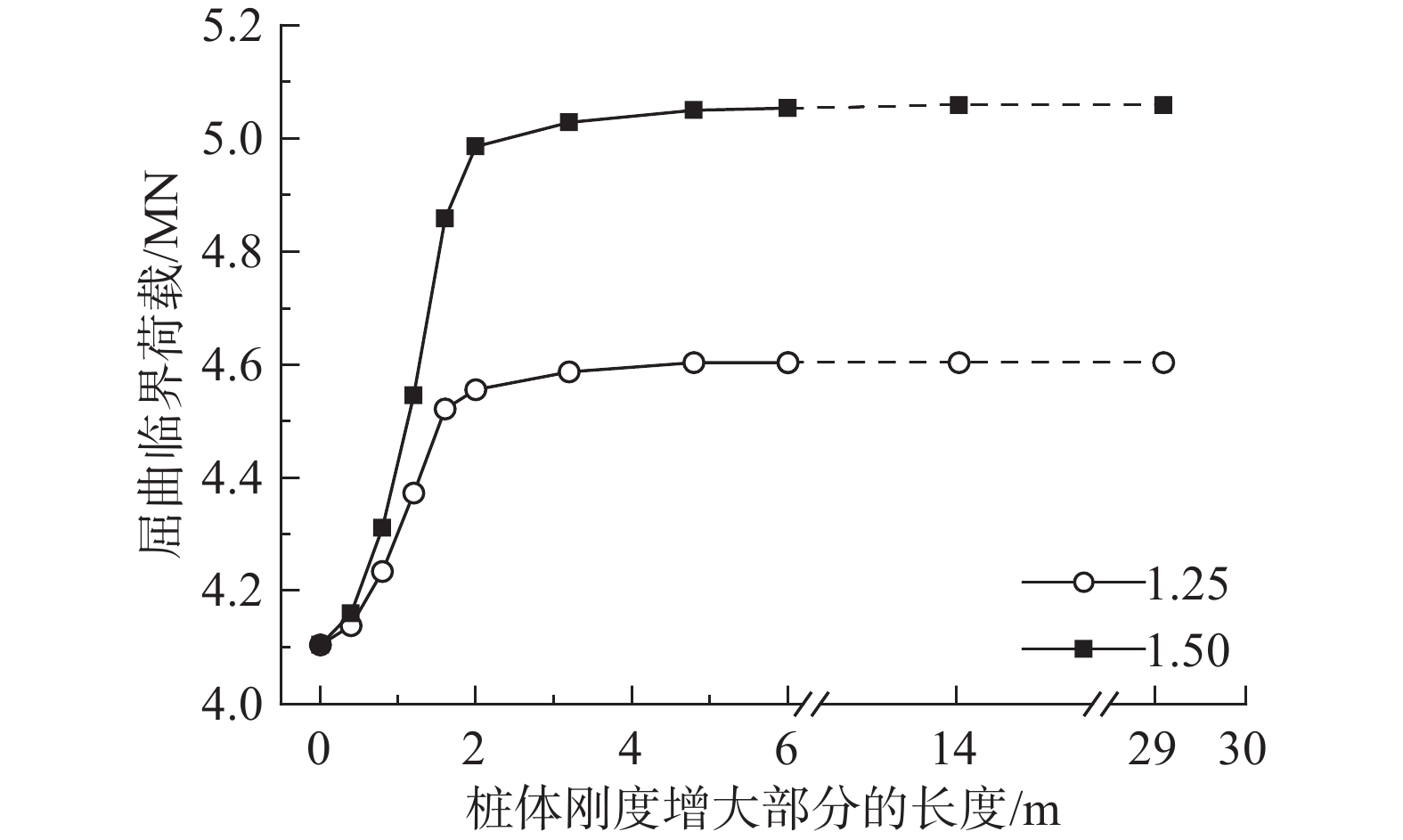
增大桩体刚度是提高微型钢管桩屈曲临界荷载的有效措施，且桩体屈曲类型为桩体上半段的局部屈曲，故以上述工程实例为基础，选取桩体刚度增大系数为1.25、1.5，分析从桩顶开始增大不同长度的桩体刚度对屈曲临界荷载的影响，如图13所示。

图  13  增大不同长度桩体的刚度下的屈曲临界荷载

Figure  13.  Buckling critical loads for increasing stiffness of piles with different lengths

下载: 全尺寸图片 幻灯片

由图13可知，当桩体刚度增大部分的长度小于2 m时，屈曲临界荷载随长度的增加显著增大；当长度为2 m时，与未增强桩体刚度相比，两个桩体刚度增大系数下的屈曲临界荷载分别增大了11.0%、21.5%。当长度大于6 m后，屈曲临界荷载基本不再随长度的增加而改变。当桩体全长范围内桩体刚度增大时，与未增强桩体刚度相比，两种桩体刚度增大系数下的屈曲临界荷载分别增大了12.2%、23.2%，仅略大于长度为2 m时的增大幅度。因此，在微型钢管桩设计时，可通过增大桩顶附近的桩体刚度，有效提高屈曲临界荷载。

3.4.4   桩顶自由段长度

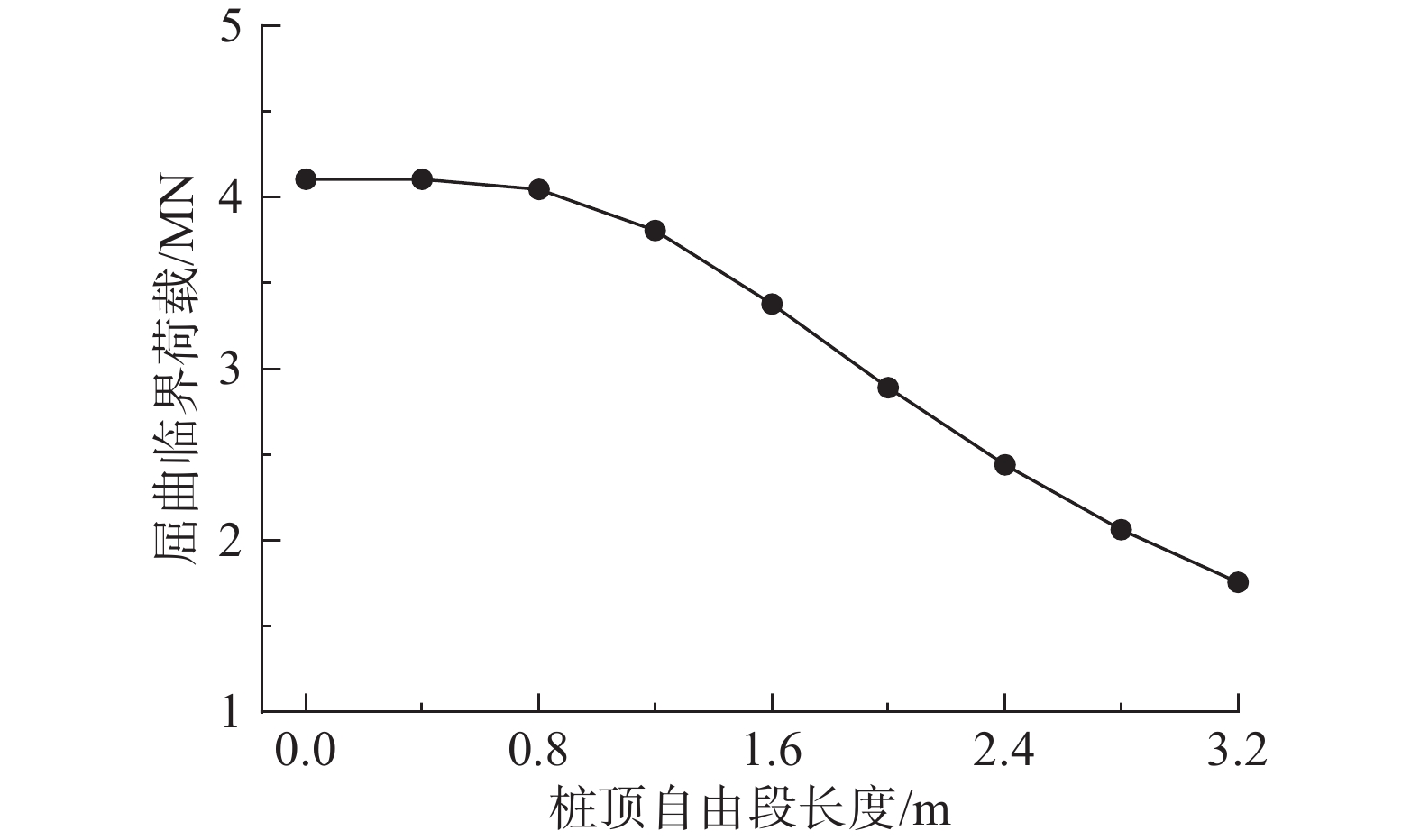
施工完毕后，建筑后续使用过程中地基仍可能因黄土遇水湿陷变形或填筑土体蠕变变形导致建筑局部筏板或承台下产生空穴，使微型桩桩顶产生自由段，其长度一般较短。故以上述工程实例参数为基准，选取桩顶自由段长度为0 m~3.2 m，分析其对微型钢管桩屈曲临界荷载的影响，如图13所示。

从图14可知，微型钢管桩屈曲临界荷载随桩顶自由段长度的增加呈非线性减小，减小速率逐渐增大。当自由段长度小于等于0.8 m时，屈曲临界荷载基本不变；当该长度大于0.8 m后，屈曲临界荷载开始急速降低；当该长度为2.0 m时，降低为无桩顶自由段情况下屈曲临界荷载的70.4%；当该长度为3.2 m时，降低为无桩顶自由段情况下屈曲临界荷载的42.8%。结合桩身挠曲线对屈曲临界荷载急速降低的原因进行分析，当自由段长度为1.2 m时，桩身最大水平位移正好位于土层顶面处，其后桩身最大水平位移均出现在地面以上桩体范围内，屈曲临界荷载从由地面以下桩体控制逐渐向由地面以上桩体控制过渡，相应的，屈曲临界荷载开始急速降低。因此，在黄土高填方区采用微型钢管桩纠倾加固时，需密切关注桩周土体是否产生较大沉降，导致桩体出现露出地面的情况，并及时采取相应措施。

图  14  不同桩顶自由段长度下的屈曲临界荷载

Figure  14.  Buckling critical load for different lengths of free section of pile

下载: 全尺寸图片 幻灯片

4   结 论

本文基于静力平衡法，提出了轴心荷载下微型钢管桩屈曲临界荷载计算方法，利用试验及数值模拟结果验证其合理性，并针对重要参数进行分析，得到以下几点结论：

(1) 桩侧土体间的剪切作用对桩体屈曲临界荷载存在较大影响，表明了考虑桩侧土体受力变形连续性的重要性。

(2) 处于屈曲临界状态时，桩体挠曲线为多个半波曲线，且极值均随深度的增加逐渐减小，减小速率与桩侧土抗力显著相关。当存在有效桩侧土体约束时，桩体上半段的水平位移远远大于其余部分，其屈曲特性由桩体上半段决定。

(3) 负摩阻力主要在桩体屈曲长度范围内发挥作用，当桩侧土抗力越小时，屈曲长度越大，负摩阻力对屈曲临界荷载的降低程度相对越明显，但仍处于较低水平，为简化计算，可忽略负摩阻力的影响。