STUDY ON CROSS-SECTIONAL RESISTANCE OF LASER-WELDED STAINLESS STEEL T-SECTION STUB COLUMNS UNDER AXIAL COMPRESSION
-
摘要:
该文针对激光焊接不锈钢T形截面构件的残余应力和轴压截面承载力进行研究，试验部分开展了不锈钢材性试验、6个试件的纵向残余应力测定以及21个短柱试件的轴压试验，提出了构件的纵向残余应力简化分布模型，得出了短柱试件轴压的局部屈曲模态和截面承载力。利用ABAQUS建立短柱试件轴压有限元模型，基于试验结果验证有限元模拟加载的准确性，进而对219个短柱构件进行数值分析。结合试验和有限元模拟结果，对我国现行《不锈钢结构技术规程》CECS410：2015中构件轴压截面承载力设计方法针对激光焊接T形截面的适用性进行评估，表明现行规范设计方法计算结果偏于保守。通过引入应变硬化系数和调整有效宽度折减系数，对原有公式进行修正，修正后的设计公式适用于预测激光焊接不锈钢T形截面构件的轴压截面承载力。
Abstract:It presents experimental and numerical studies on the residual stress and cross-sectional compression resistance of laser-welded stainless steel T-section stub columns. The material testing, 6 membrane residual stress measurements and 21 stub column tests were carried out in the testing program. A simplified distribution model for membrane residual stresses in laser-welded stainless steel T-section was proposed, and the local buckling mode and cross-sectional resistance of stub column under axial compression were obtained. The finite-element models of the tested stub column specimens were developed by ABAQUS, and the accuracy of the FE models was verified based on the test results. Then, parametric analysis was performed to analyze 219 FE models of laser-welded stainless steel T-section stub columns. Based on the test and parametric analysis results, the applicability of the design formulas of the cross-sectional compression resistance of stub columns in current Chinese code ‘Technical Specification for Stainless Steel Structures’ – CECS410:2015’ to laser-welded stainless steel T-section was evaluated. The evaluation shows that the design results of current Chinese specification are conservative. Through the introduction of strain hardening coefficient and adjusting the effective width reduction coefficient, the existing specification is modified. The modified design formulas can accurately predict the cross-sectional compression resistance of laser-welded stainless steel T-section stub columns.
-
采用耐腐蚀性强的不锈钢取代碳钢和低合金钢，是解决钢结构腐蚀影响[1 − 2]的有效途径之一。不锈钢构件结构性能研究可为此类构件在建筑、桥梁及海洋结构中的应用奠定基础[3 − 7]。相较传统焊接工艺，激光焊接(LW)过程输入热量低、热影响区集中，焊接残余应力峰值低，近年来已大量应用于工程建造领域[8 − 9]。不锈钢材料价格高是影响其结构推广应用的重要因素，提高结构设计效率是解决这一问题的手段之一。基于以上原因，有必要对激光焊接不锈钢构件结构性能进行研究，评估已有设计方法的设计效率，提出准确的设计方法。
国内外学者对激光焊接不锈钢构件焊接残余应力、截面承载力及稳定承载力均有较深入探索。在残余应力方面，GARDNER等[10]和FILIPOVIĆ等[11]分别对H形截面和角钢截面构件的焊接残余应力进行测定，表明激光焊接残余应力峰值低于传统焊接，并提出截面残余应力简化分布模型。在截面承载力方面，GARDNER等[10]深入研究了H形截面短柱的轴压性能，RAN等[12 − 13]对其试验结果进行补充并开展短柱压弯性能研究。BU等[14]探讨了H形截面构件的截面抗弯承载能力，FILIPOVIĆ等[11]和LIANG等[15]分别对角钢短柱的轴压性能和槽钢短柱的压弯性能开展了研究工作。在稳定承载力方面，GARDNER[10]、FILIPOVIĆ等[11]和RAN等[12]分别研究了H形截面构件和角钢截面构件在轴压下的稳定性能，RAN等[16 − 17]和BU等[18]通过对H形截面构件的压弯性能进行试验研究及数值分析，进一步探讨了构件在复合加载情况下的性能。THEOFANOUS等[19]填补了角钢和槽钢构件弯矩作用下整体稳定性能的试验数据空白。以上学者通过试验研究和数值分析方法，对现行不锈钢结构欧洲规范EN1993-1-4[20]、美国规范AISC Design Guide 27[21]及连续强度法[22]截面和稳定承载力设计方法，针对激光焊接不锈钢构件的设计效率进行评估，并在此基础上对已有设计方法进行改进，改进方法提高了设计效率。
T形截面钢构件制造简单、安装便捷，能够适应不同的受力要求和空间限制，且相比其他截面形式，能够在提供相同刚度和承载力的情况下减少材料用量，进而降低成本，广泛应用于梁、柱、支撑及桁架等构件。然而对此类截面构件结构性能的研究尚存在欠缺，本文对激光焊接不锈钢T形截面构件截面承载性能进行研究，以期为此类构件的结构应用提供试验数据及理论基础。
为探究激光焊接不锈钢T形截面短柱的轴压截面承载力，对6个试件进行残余应力测定，提出残余应力简化分布模型；对21个短柱试件进行轴压试验，得出试件的局部屈曲模态和截面承载力。基于试验结果，验证有限元模拟加载的准确性，分析残余应力对截面承载力的影响；利用数值分析，得到更多截面尺寸短柱构件的截面承载力数据；进而对现行《不锈钢结构技术规程》CECS410：2015[23](以下简称CECS410)中构件轴压截面承载力设计方法，针对激光焊接T形截面的适用性进行评估及改进。本文中部分试验数据在文献[24]中用于评估欧洲和美国现行不锈钢结构设计规范及连续强度法对激光焊接不锈钢T形截面构件轴压截面承载力的设计效率，可供读者参考。
1 试验研究
1.1 试件设计
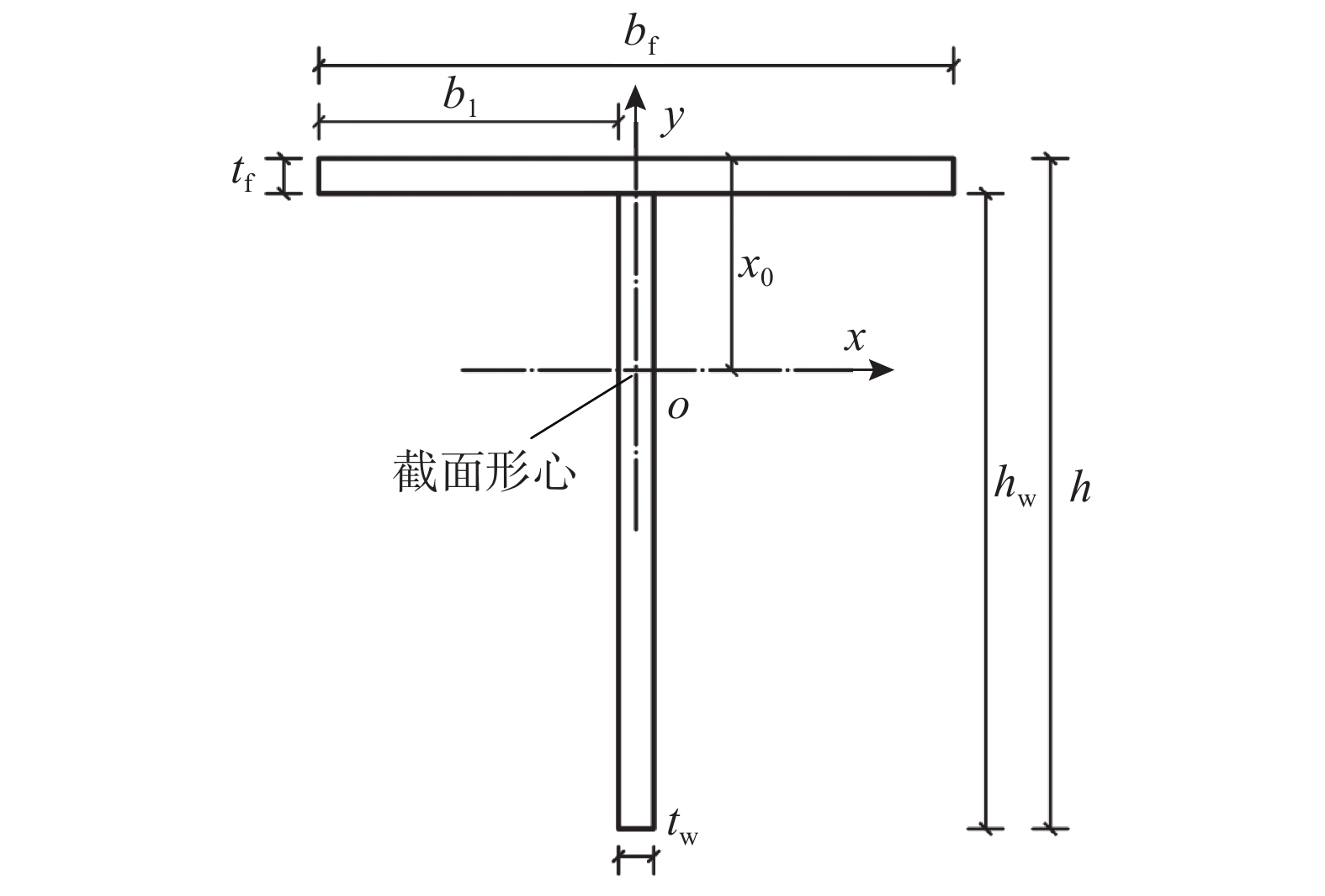
为提高试验数据的代表性，所用试件采用5种截面轮廓尺寸，以高×宽表示分别为60 mm×60 mm、60 mm×90 mm、60 mm×120 mm、90 mm×90 mm、120 mm×120 mm，翼缘和腹板的板件名义厚度选择3 mm、5 mm、8 mm 3种厚度，共计15种截面尺寸，通过S30408不锈钢板激光焊接而成，截面尺寸符号如图1所示。本文中试件编号代表试件截面名义尺寸，例如“T60-90-3”，代表截面名义高度和宽度分别为60 mm和90 mm，腹板和翼缘名义厚度为3 mm，后缀“-1，-2”表示重复试件(下同)。
共计21个短柱试件，长度满足ZIEMIAN[25]建议的min (2d+250 mm, 3d)≤L≤max(20ry, 5d)。其中，d是构件截面轮廓较大值，ry是截面绕强轴的回转半径，确保短柱试件发生板件局部屈曲的强度破坏，本文中短柱试件的设计长度取截面高度的3倍(L=3h)。CECS410在构件截面承载力设计中，通过对组成构件各板件宽厚比限值的方式区分了构件截面类型：各板件宽厚比均小于限值时为全截面有效构件，即承载极限可达到全截面名义屈服强度；宽厚比大于限值板件存在时为部分截面有效构件，即承载极限达不到全截面名义屈服强度，根据有效截面计算截面承载力。板件宽厚比限值与构件的受力状态、成型方式及组成板件的钢材型号、支承类型有关，本文将宽厚比小于限值的板件记为紧凑型，反之记为薄柔型。T形截面腹板和翼缘均属于非加劲板件，S30408不锈钢板焊接成型的构件在轴压时对非加劲板件的宽厚比限值为11，由此来判断构件的板件类型，进而对构件截面进行分类。当构件各组成板件均为紧凑型时，记为紧凑截面；当构件含有薄柔型板件时，记为薄柔截面。加工时，对短柱试件两端采用线切割工艺切平处理，以保证端部平整度；取距两端25 mm的两个截面和中部截面测量值的均值，作为短柱试件实际几何尺寸；板件宽厚比及类型、试件截面类型以及实测几何尺寸见表1。
表 1 短柱试件实测几何尺寸Table 1. Measured geometric dimensions of stub column specimens试件编号 截面高度
h/mm截面宽度
bf/mm板件厚度
t/mm试件长度
L/mm形心位置
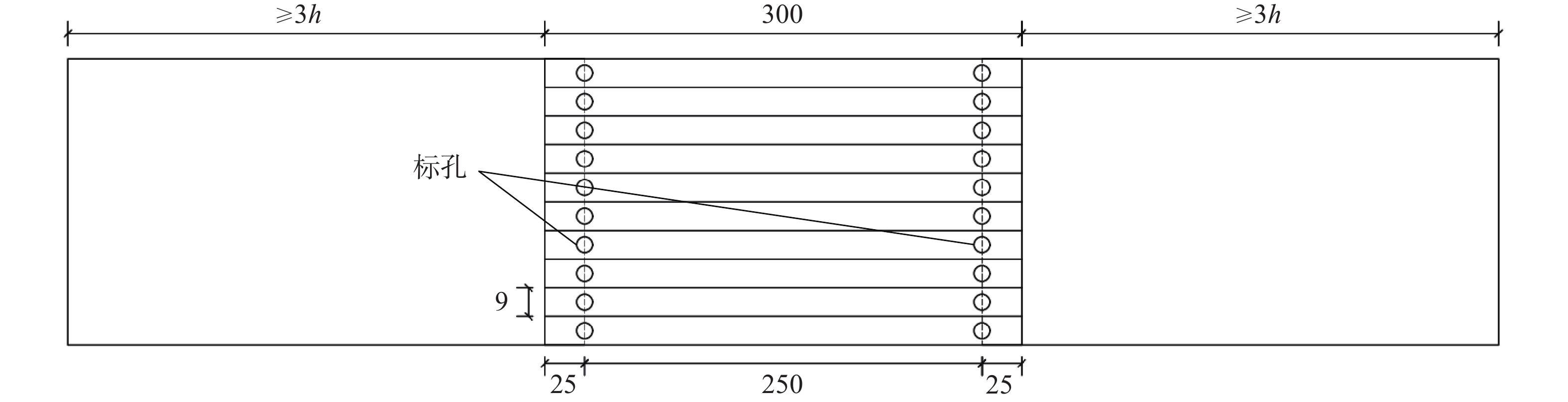
x0/mm腹板翼缘宽厚比及板件类型 试件截面类型 翼缘宽厚比b1/tf 翼缘类型 腹板宽厚比hw/tw 腹板类型 T60-60-3 62.42 59.81 2.89 179.49 17.2 9.85 紧凑型 20.67 薄柔型 薄柔截面 T60-60-5 64.49 60.89 4.74 179.42 18.6 5.92 紧凑型 12.63 薄柔型 薄柔截面 T60-60-8-1 67.39 60.69 7.62 179.41 20.7 3.48 紧凑型 7.85 紧凑型 紧凑截面 T60-60-8-2 67.32 60.73 7.63 179.41 20.7 3.48 紧凑型 7.83 紧凑型 紧凑截面 T60-90-3 62.52 89.59 2.89 269.42 14.0 14.95 薄柔型 20.71 薄柔型 薄柔截面 T60-90-5 64.53 89.58 4.73 269.48 15.5 8.95 紧凑型 12.67 薄柔型 薄柔截面 T60-90-8-1 67.82 89.52 7.64 269.43 17.3 5.38 紧凑型 7.90 紧凑型 紧凑截面 T60-90-8-2 67.84 89.54 7.64 269.47 17.3 5.37 紧凑型 7.88 紧凑型 紧凑截面 T60-120-3 62.68 119.83 2.89 359.12 11.9 20.30 薄柔型 20.68 薄柔型 薄柔截面 T60-120-5-1 64.42 119.88 4.74 359.52 13.2 12.17 薄柔型 12.60 薄柔型 薄柔截面 T60-120-5-2 64.43 119.77 4.73 359.48 13.2 12.16 薄柔型 12.62 薄柔型 薄柔截面 T60-120-8 67.11 119.76 7.63 359.37 15.1 7.35 紧凑型 7.83 紧凑型 紧凑截面 T90-90-3-1 92.72 89.63 2.87 269.82 24.7 15.06 薄柔型 31.41 薄柔型 薄柔截面 T90-90-3-2 92.68 89.62 2.88 269.77 24.7 15.04 薄柔型 31.17 薄柔型 薄柔截面 T90-90-5 94.33 89.61 4.73 269.92 26.0 8.97 紧凑型 18.95 薄柔型 薄柔截面 T90-90-8-1 97.48 89.82 7.63 269.88 28.2 5.40 紧凑型 11.82 薄柔型 薄柔截面 T90-90-8-2 97.53 89.83 7.62 269.87 28.2 5.40 紧凑型 11.82 薄柔型 薄柔截面 T120-120-3-1 122.68 119.70 2.88 359.51 32.2 20.28 薄柔型 41.73 薄柔型 薄柔截面 T120-120-3-2 122.73 119.62 2.90 359.48 32.2 20.19 薄柔型 41.32 薄柔型 薄柔截面 T120-120-5 124.22 119.48 4.73 359.86 33.5 12.15 薄柔型 25.22 薄柔型 薄柔截面 T120-120-8 127.42 119.88 7.63 359.71 35.7 7.36 紧凑型 15.72 薄柔型 薄柔截面 采用锯割法对残余应力进行测定，将试件截面划分成若干个条带，对每个条带的两端进行标孔，而后利用线切割工艺对试件先后进行板件和条带分割，根据条带分割前后两端标孔的间距变化，可得到截面相应位置的纵向残余应力。采用YB-25手持应变仪测量标孔切割前后的间距，其标距L0=250 mm，故而残余应力试件长度取300 mm。根据ZIEMIAN[25]建议的残余应力试件取材位置，试件两端距离加工母材端部不小于1.5倍的试件截面较大尺寸，但考虑到短柱试件的加工，试件两端距离加工母材端部的长度需满足不小于3倍试件截面高度尺寸的要求。在每个条带距离端部25 mm处加工直径为2 mm的标孔，并进行深度为0.5 mm的倒角处理以清除毛刺方便测量，试件取材位置和条带切割示意图如图2所示。综合考虑标孔的应力重分布影响和准确反映截面残余应力分布，各条带切割宽度定为9 mm，进而试件截面选择T90-90，三种板件厚度的试件各取2个。
![]()
图 2 残余应力试件取材位置和条带切割示意 /mmFigure 2. Selection position and strip cutting diagram of residual stress specimens1.2 不锈钢材性试验
不锈钢拉伸材性试验在300 kN多功能试验机上进行，参考《金属材料拉伸试验 第1部分：室温试验方法》(GB/T 228.1−2010)[26]中相关要求，采用线切割工艺在3种厚度的试件同批钢材原板上沿轧制方向切取标准拉伸试件。材性试件的设计尺寸参照《钢与钢产品力学性能试验取样位置及试样制备》(GB/T 2975−2018)[27]中相关规定，在3种不同厚度的钢板上各取2个试件，按厚度分类记为T3、T5、T8，根据规范公式计算的对应原始标距分别为40 mm、50 mm、65 mm。材性试验过程如图3所示，实测试件拉伸应力-应变曲线如图4所示，试验得到的部分材性参数见表2。
表2中：E为不锈钢弹性模量；σ0.2为塑性应变为0.2%对应的应力(名义屈服强度)；σu为极限抗拉强度；εf为断后伸长率；n、m为ARRAYAGO[28]的不锈钢本构关系模型相关参数，更多材性参数详见文献[24]。材性试验结果表明，不锈钢拉伸的应力-应变曲线连续且光滑，σu约为σ0.2的2.6倍，材料表现出良好的延性和应变硬化效应。
表 2 S30408不锈钢材料性能参数Table 2. Material properties of S30408 stainless steel plates厚度 E/GPa σ0.2/MPa σu/MPa εf/(%) n m T3 191.8 274 754 62 6.33 2.02 T5 192.3 286 774 59 6.81 2.04 T8 186.8 281 715 62 7.58 2.09 注：E为弹性模量；σ0.2为0.2%塑性应变对应的应力(名义屈服强度)；σu为极限抗拉强度；εf为断后伸长率；n、m为ARRAYAGO[28]不锈钢本构模型相关参数。 1.3 残余应力测定与拟合
为考虑试验过程中温度变化所造成的温度应力对残余应力测量结果的影响，制作一个和试件相同材质的不锈钢板条，打上测量孔，作为温度参考杆，每次测量各测孔间距时，同时量测对应温度参考杆读数。条带的分割借助线切割方法进行，初始标孔间距记为r1，条带释放残余应力后的标孔间距记为r2，分割前后温度参考杆间距分别记为t1、t2，均采用YB-25型手持应变仪进行量测，精确度可达到0.001 mm。根据条带因释放残余应力在标孔间距长度上所造成的形变，结合应力-应变关系，通过式(1)可求得相应位置的残余应力σr，切割过程如图5所示，典型试件分割后条带示意如图6所示。
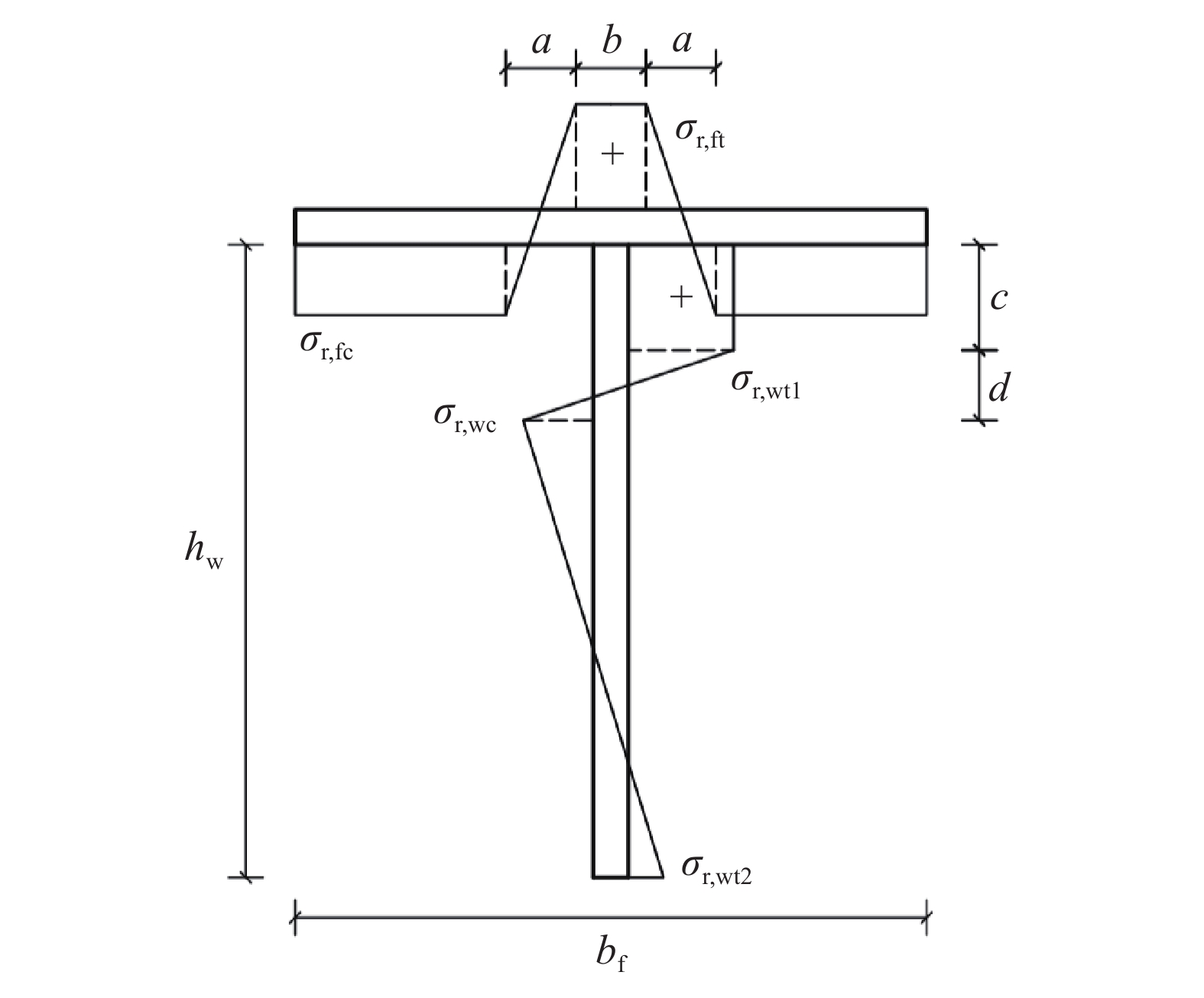
σr=E(r1−t1)−(r2−t2)L0 (1) 根据实测残余应力大小与分布形态，用材料的名义屈服强度σ0.2对实测数值进行正则化，拉应力以正值(+)表示、压应力以负值(-)表示。利用腹板高度和翼缘宽度对条带位置进行归一化处理，使其可适用于所有尺寸截面，汇总结果如图7所示。根据实测残余应力数值，提出激光焊接T形截面的残余应力简化分布模型如图8所示，各参数定义见表3。尚未见有针对传统焊接不锈钢T形截面的残余应力分布模型，本文根据H形截面和T形截面的几何关系，将文献[10]提出的激光焊接不锈钢H形截面残余应力简化分布模型，沿y轴对称取1/2与试验数据进行比对，对比结果如图7所示。由图7可知，两种截面在焊缝处的残余应力峰值表现出较好的一致性。
![]()
图 7 实测残余应力与预测模型的比较Figure 7. Comparison of measured residual stresses and predictive models表 3 建议残余应力模型参数Table 3. Proposed model factor for residual stress模型参数 σr,ft=σr,wt1 \boldsymbol{\sigma}_{\text {r,wt2}} a b c d 参数值 0.5 \sigma_{\text {0.2}} 0.1 \sigma_{\text {0.2}} 0.1bf 0.1bf 0.05hw 0.1hw 注：1) \sigma_{ {\mathrm{r, fc}}} , \sigma_{ {\mathrm{r, wc}}} 由截面应力自平衡得到；2) f和w分别为翼缘和腹板；3) t和c分别为拉力和压力。 1.4 短柱试件轴压试验
1.4.1 局部初始几何缺陷测量
在进行短柱轴压试验前，采用铣床测量所有短柱试件的初始几何缺陷，以验证试件的加工精度及为有限元模拟提供缺陷数据。首先，用机械式百分表对铣床工作面进行量测，保证工作台面的平整度小于±0.01 mm；而后，将试件固定在铣床工作台面上，分别对腹板和翼缘进行测量，通过摇动铣床手柄在试件横截面以2 mm的间隔采集数据，以反映板件的初始几何缺陷。针对试件中部以及距离两端部30 mm处的3个横截面进行测量，测量过程如图9所示。取试件组成板件缺陷幅值最大绝对值作为短柱试件的缺陷幅值{\omega _0}，结果汇总于表4。根据《钢结构工程施工质量验收标准》[29]规定，对于焊接H形截面的允许偏差为b/100(b为截面板件最大外伸长度，下同)且不大于2.0 mm，本文中T形截面仍采用这一限值。短柱试件的最大缺陷幅值为0.11 mm，最大比值达到b/545，均满足规范要求。
表 4 短柱试件轴压试验结果与有限元模拟结果比较Table 4. Comparison between stub column axial compression test and FE results试件编号 \overline{\lambda}_{\mathrm{p}} 试验结果 模型不同缺陷幅值对应的Nu,FE/Nu,test \omega_0 /mm \omega_0 /b Nu,test/kN {\varDelta}_{\text {u,test}} /mm \omega_0 b /50 b /100 b /200 T60-60-3 0.82 0.04 1/1500 79.03 0.76 1.02 0.98 0.99 1.00 T60-60-5 0.51 0.05 1/1200 182.06 1.74 1.02 0.97 0.98 0.99 T60-60-8-1 0.32 0.09 1/666 350.35 5.51 1.02 0.95 0.96 0.98 T60-60-8-2 0.32 0.05 1/1200 324.17 4.32 0.99 0.96 0.97 0.99 T60-90-3 0.97 0.03 1/1500 83.22 1.35 1.00 0.98 0.99 1.00 T60-90-5 0.60 0.03 1/2000 200.48 1.62 1.00 0.97 0.98 1.00 T60-90-8-1 0.38 0.10 1/600 403.38 5.88 1.01 0.96 0.96 0.97 T60-90-8-2 0.38 0.04 1/1500 365.62 3.73 0.98 0.97 0.97 0.98 T60-120-3 1.15 0.06 1/1000 92.52 1.01 0.99 0.98 0.98 0.99 T60-120-5-1 0.71 0.03 1/2000 230.87 1.62 0.99 0.98 0.98 0.99 T60-120-5-2 0.71 0.07 1/857 225.46 1.79 1.00 0.98 0.99 1.00 T60-120-8 0.44 0.11 1/545 449.43 3.80 0.99 0.97 0.99 0.99 T90-90-3-1 1.22 0.07 1/1286 91.91 1.02 1.02 1.00 1.01 1.02 T90-90-3-2 1.22 0.07 1/1286 91.74 1.03 1.02 1.00 1.01 1.02 T90-90-5 0.75 0.03 1/3000 217.19 1.35 0.99 0.96 0.98 0.99 T90-90-8-1 0.48 0.06 1/1500 418.02 1.99 0.98 0.97 0.97 0.98 T90-90-8-2 0.48 0.03 1/3000 412.91 2.09 0.98 0.97 0.98 0.98 T120-120-3-1 1.63 0.09 1/1333 102.08 1.25 0.99 0.97 0.98 0.99 T120-120-3-2 1.63 0.08 1/1500 98.45 1.38 0.99 0.97 0.98 0.99 T120-120-5 1.00 0.05 1/2400 229.12 1.80 0.99 0.97 0.98 0.99 T120-120-8 0.63 0.06 1/2000 530.38 2.11 1.01 0.99 1.00 1.01 平均值 1.01 0.97 0.98 0.99 标准差 0.01 0.01 0.01 0.01 注： \overline{\lambda}_{\mathrm{p}} 为试件全截面柔度系数； \omega_0 为实测试件初始几何缺陷幅值。 1.4.2 加载方案
在1000 kN液压机上对短柱试件施加轴向位移控制加载，加载速率为0.2 mm/min，安装试件时将试件形心与试验机支座定位线的交点对齐，令上、下形心与加载装置的中轴线在一条直线，以保证轴压加载。为得到短柱试件的轴向压缩变形，对每个短柱试件布置4个数字位移计(LVDT)、6个应变测点(SG)，通过数据采集仪(DATASCAN)记录荷载、应变和位移等试验数据，加载装置如图10所示。短柱试件安装完成后，先进行预加载。预加载阶段，可根据各应变片数值的增长率判断试件端面平整度，如不平整则通过打磨端部调整，直到各应变片数值同步增长，确保端部与试验台面完全接触且顶紧；仪器数据归零后开始正式加载，当荷载下降到极限荷载的70%时停止加载。
1.4.3 试验过程
加载开始时，试件无明显变形，随着加载的进行，试件的组成板件逐渐出现内凹外凸现象，这导致板件凹凸两侧应变片数值不再同步增长。达到极限荷载后，荷载随轴向位移的继续增大而下降，凸起侧位置的应变测点压应变数值逐渐减小，最后发展为拉应变，腹板和翼缘中部发生明显的局部鼓曲和凹陷现象。在荷载下降到极限荷载70%时停止加载，卸载后试件板件沿长度方向残留了塑性鼓曲变形，所有短柱试件卸载后形状见图11。
1.4.4 试验结果分析
在加载初期，由于机器内部间隙以及试件未压实，位移计读数记录的短柱试件轴向变形会比实际偏高，荷载与轴向变形的不匹配造成试件初始阶段荷载-轴向位移曲线斜率偏低。由试验数据可知，试件加载初始阶段轴向变形处于弹性阶段，轴向位移可基于试件中部应变片数值通过式(2)计算得到，结合位移计读数可绘制出全过程荷载-轴向位移曲线。
{\delta _{\text{u}}} = L\varepsilon (2) 式中：{\delta _{\text{u}}}为轴向位移；\varepsilon 为试件中部应变片读数；L为试件长度。轴压试件的极限荷载Nu,test及对应的轴向变形{\delta _{{\text{u,test}}}}见表4。汇总后的试件轴压应力-应变曲线见图12，荷载-轴向位移曲线见图13。
![]()
图 13 试验与有限元模拟荷载-轴向位移曲线对比Figure 13. Comparison of load-axial displacement curves between test and FE simulation图12对短柱试件轴压应力-应变曲线按试件截面类型分类，所有试件均表现出良好的延性。紧凑截面试件由于组成板件较小的宽厚比，板件较大的抗弯刚度和材料的应变硬化效应有利于局部屈曲后承载力的发展，其极限荷载对应的截面平均应力均高于名义屈服强度；含有紧凑型板件的薄柔截面试件，其极限荷载对应的截面平均应力略高于名义屈服强度；组成板件均为薄柔型的薄柔截面试件，板件较大的宽厚比导致抗弯刚度较小，局部屈曲后形变快速发展而达到极限荷载，其极限荷载对应的截面平均应力低于名义屈服强度。为准确描述截面板件宽厚比对构件截面承载力的影响，引入构件全截面柔度系数{\overline \lambda _{\text{p}}}，由式(3)计算得到：
{\overline \lambda _{\text{p}}} = \sqrt {{\sigma _{0.2}}/{\sigma _{{\text{cr}}}}} (3) 式中，构件全截面板件的弹性屈曲应力{\sigma _{{\text{cr}}}}通过软件CUFSM[30]计算得到，该软件计算已考虑了板件间的相互作用，短柱试件的全截面柔度系数见表4。
2 有限元模型验证
2.1 有限元模型的建立
本文通过ABAQUS建立短柱试件轴压的有限元模型，采用S4R 4节点壳单元定义网格类型，经收敛性分析验证网格尺寸取为3 mm较为合适。根据材性试验得出的ARRAYAGO[28]不锈钢本构关系参数，进行真实应力-塑性应变的转换后输入，完成模型材性的定义。因整个试验过程未出现试件端部滑移现象，故而可将试件模型两端截面采用相互作用的方式绑定到RP1、RP2两个参考点(即截面形心)，对固定端(RP1)参考点的6个自由度及加载端(RP2)参考点除轴向平动外的5个自由度施加约束，通过对RP2施加U3方向平动完成加载，如图14所示。分析过程分为屈曲分析和静力分析2步：第一步使用屈曲分析步得到试件的弹性屈曲模态，将符合试验现象的模态(一阶)采用*IMPERFECTION命令定义幅值大小，作为初始几何缺陷输入第二步的静力分析步中，采用弧长法求解。为提高有限元模拟的准确性，根据文献[29]对板件局部缺陷限值的方法，通过输入四种缺陷幅值对模拟结果进行对比：① 实测局部初始几何缺陷{\omega _{\text{0}}}；② b/200；③ b/100；④ b/50。采用提出的激光焊接不锈钢T形截面残余应力分布模型，使用*INITIALCONDI TION(TYPE=STRESS)命令定义静力分析步的初始应力场，模型的残余应力分布如图14所示。
2.2 有限元模拟准确性验证
采用建立的有限元模型对21个短柱试件进行数值分析，表4汇总了试验和有限元模拟结果的对比情况，表中Nu,FE为有限元模拟的试件极限荷载。图13针对试验和有限元模拟(输入实测缺陷幅值)得出的试件加载荷载-轴向位移曲线进行了对比，图15展示了短柱试件T60-90-8(紧凑截面)和T120-120-3(薄柔截面)的试验和有限元模拟典型破坏模态，比对结果表明，试验和有限元模拟结果略有偏差，但总体吻合良好。综上，本文建立的有限元模型能够准确模拟激光焊接不锈钢T形截面轴压短柱加载响应，可用于后续的参数分析中。
![]()
图 15 典型短柱试件试验与有限元模型破坏模态对比Figure 15. Comparison of failure modes for typical stub column specimens between test and FE simulation3 有限元模拟
3.1 建立构件截面承载力数据库
基于已验证的有限元模型，采用ABAQUS对构件进行数值分析可以解决试验研究数据不足的缺点，将ABAQUS各模块编译成对应的Python脚本代码进行建模和求解以提高效率。
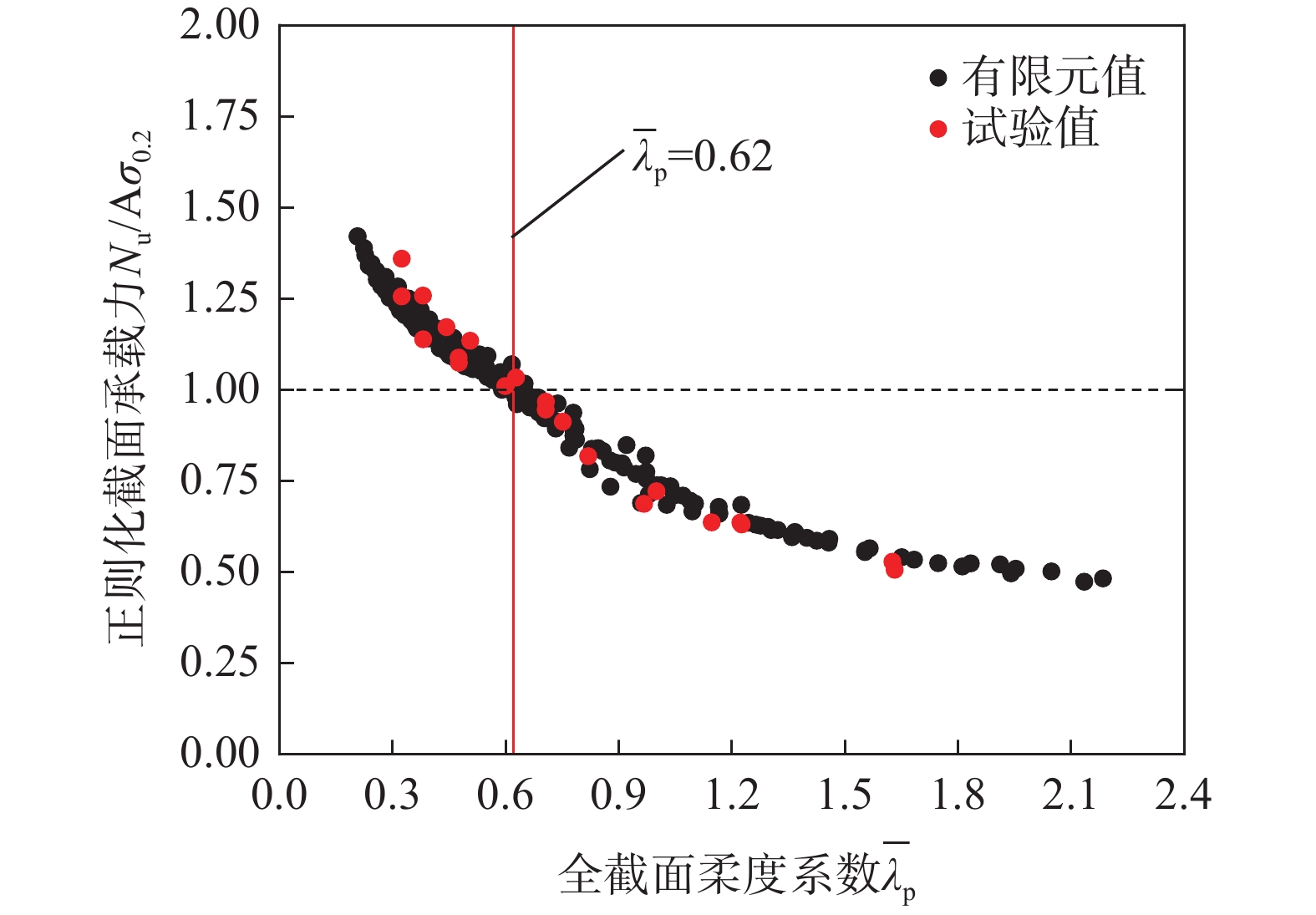
本节对207个构件有限元模型进行了数值分析，其中截面高度h和截面宽度bｆ的取值范围为50 mm~180 mm，板件厚度t为2 mm~14 mm，构件长度取截面高度的3倍。构件的单板宽厚比范围为3.67~54.5，全截面柔度系数范围为0.21~2.18，涵盖了紧凑截面和薄柔截面。构件有限元模型采用本文建议的残余应力简化分布模型定义初始应力场，偏于安全考虑，初始几何缺陷幅值统一取b/100。图16给出了所有研究构件截面承载力随全截面柔度系数的分布情况，横坐标为全截面柔度系数，纵坐标为经过全截面屈服荷载正则化的构件截面承载力(以下简称Nu/Aσ0.2)，可以看出，{\overline \lambda _{\text{p}}}=0.62划分了构件截面承载力是否能达到全截面名义屈服的界限。
![]()
图 16 截面承载力随全截面柔度系数分布Figure 16. Distribution of cross-sectional resistance with full section slenderness coefficient3.2 焊接残余应力影响分析
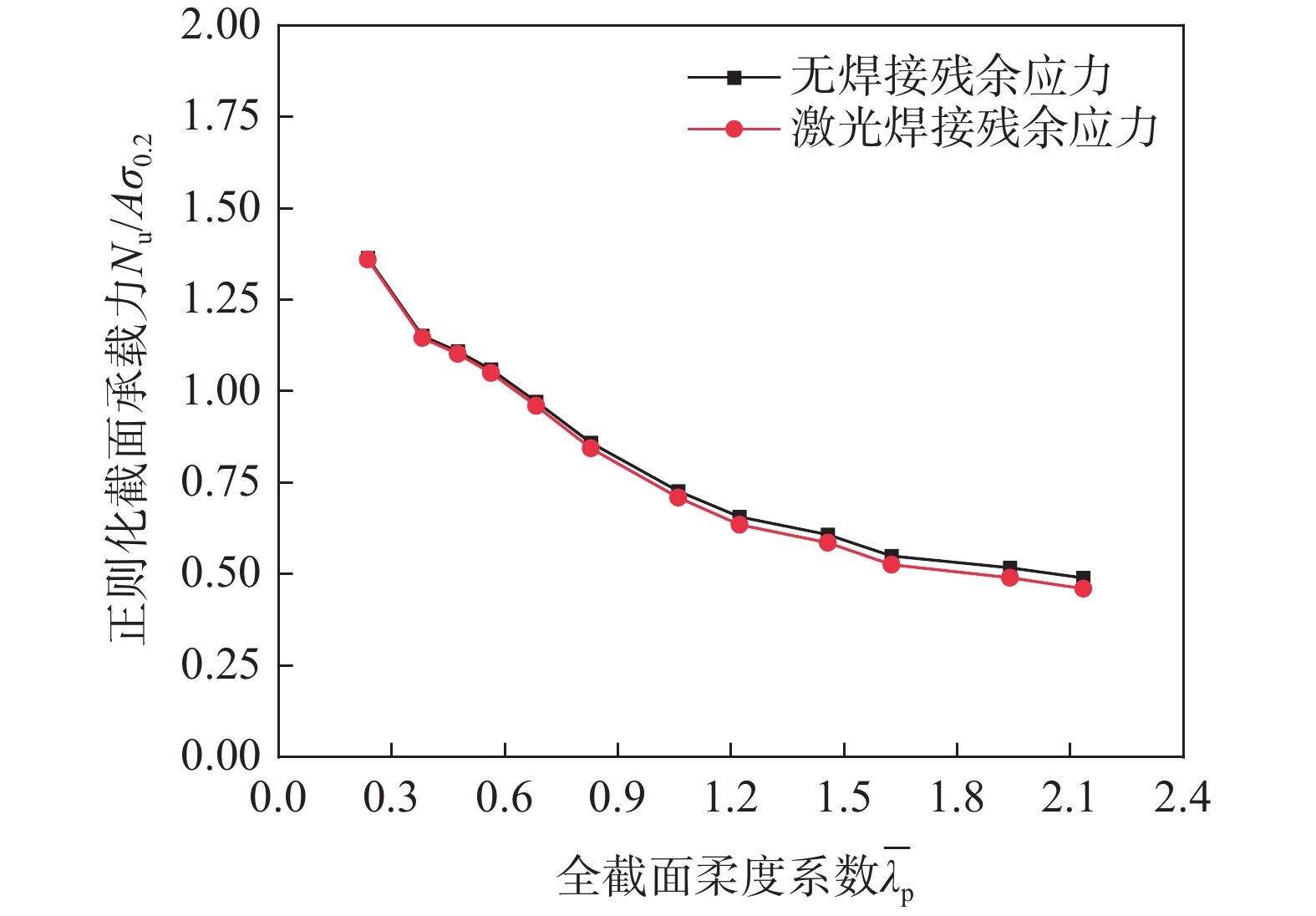
为研究焊接残余应力对T形截面轴压短柱截面承载力的影响，本节选取全截面柔度系数范围为0.23~2.13的12种不同截面构件，分别对构件有限元模型进行计算，定义激光焊接残余应力为初始应力场和无初始应力场两种情况。模型缺陷幅值均取b/100，激光焊接残余应力分布采用本文提出的建议模型。有、无焊接残余应力的截面承载力对比曲线如图17所示。
比对结果表明，随着截面柔度系数的增大，激光焊接残余应力对截面承载力的降低程度越大，当{\overline \lambda _{\text{p}}}=0.62时，降低约1%；当{\overline \lambda _{\text{p}}}=2.1时，降低约3%。由于板件宽厚比增大，抗弯刚度下降有利于局部屈曲后变形的发展，残余压应力的存在导致板件部分位置压应力增大而加大变形，降低构件的截面承载力，因此，焊接残余应力对薄柔截面构件截面承载力的降低程度大于紧凑截面。本文建议可结合{\overline \lambda _{\text{p}}}随截面承载力降低程度的分布关系，以(0, 0)、(0.62, 1%)、(2.1, 3%)三组数据点为依据，分别在0<{\overline \lambda _{\text{p}}}<0.62和0.62<{\overline \lambda _{\text{p}}}<2.1两段范围内采用线性插值法计算降低程度。
4 CECS410设计方法评估与改进
4.1 受压板件宽厚比限值评估
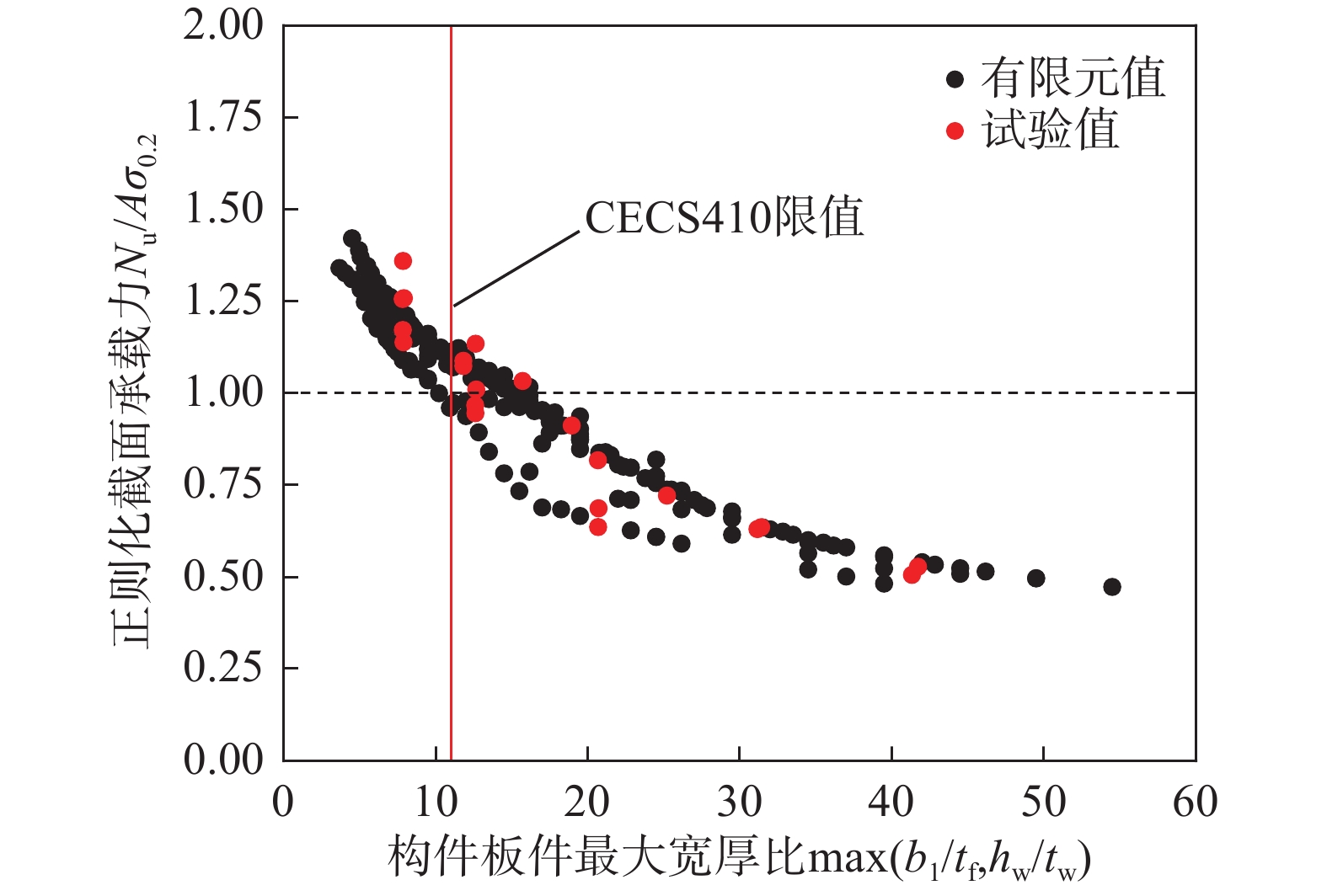
图18给出了构件截面承载力随板件宽厚比的分布情况，以组成板件较大宽厚比为横坐标，{N_{\text{u}}}/A{\sigma _{0.2}}为纵坐标绘图。
![]()
图 18 CECS410受压板件宽厚比限值评估Figure 18. Assessment of CECS410 width-to-thickness ratios for compression elements由于CECS410在设计中未考虑不锈钢材料的应变硬化效应，故而低估了构件的截面承载力。图12和图18分析均表明，区分截面类型的宽厚比限值偏于保守。
4.2 截面承载力设计公式评估
CECS410关于轴心受压构件截面承载力设计以钢纤维名义屈服为准则，未考虑材料抗力分项系数的设计公式，见式(4)：
\frac{N}{{{A_{{\text{en}}}}}} {\leqslant} {f_{\text{y}}} (4) 式中：Aen为有效净截面面积；fy为名义屈服强度( {\sigma _{0.2}} )。对于紧凑截面，Aen取净截面面积；对于薄柔截面，采用有效宽度法计算构件有效净截面，即{A_{{\text{en}}}} = \sum {{b_{\text{e}}}t} ，有效宽度计算公式见式(5)：
\frac{{{b_{\text{e}}}}}{t} = \left\{ \begin{aligned} & ({\alpha _1}{\text{ + }}{\alpha _2}\sqrt {{{\overline \lambda }_{\text{p}}}} {\text{)}}\frac{{{b_{\text{c}}}}}{t} {\leqslant} \frac{{{b_{\text{c}}}}}{t},&& {\overline \lambda _{\text{p}}} {\leqslant} 1.0 \\& \left(\frac{{{{\overline \lambda }_{\text{p}}}}}{{{\alpha _3}{{\overline \lambda }_{\text{p}}} + {\alpha _4}}}\right)\frac{{{b_{\text{c}}}}}{t},&& {\text{ 1}}{\text{.0 < }}{\overline \lambda _{\text{p}}} < {\text{1}}{\text{.5}} \\& \left(\frac{{{\alpha _5}{{\overline \lambda }_{\text{p}}} + {\alpha _6}}}{{{{\overline \lambda }_{\text{p}}}}}\right)\frac{{{b_{\text{c}}}}}{t},&& {\overline \lambda _{\text{p}}} {\geqslant} 1.5 \end{aligned} \right. (5) 式中：be为板件有效宽度；t为板件厚度；{\alpha _1} \sim {\alpha _6}为焊接成型构件的计算系数，详见表5；{\overline \lambda _{\text{p}}}和bc分别为全截面柔度系数和板件受压区宽度，计算公式详见CECS410第5.6节。
表 5 焊接构件有效宽度折减系数Table 5. Effective width reduction factor for welded components参数来源 \alpha_{1} \alpha_{2} \alpha_3 \alpha_{4} \alpha_5 \alpha_6 CECS410 1.84 −1.14 3.15 −1.72 0.086 0.62 建议公式 1.97 −1.24 2.53 −1.17 0.28 0.44 通过CECS410设计公式计算短柱试件和有限元模拟构件的截面承载力，以全截面柔度系数为横坐标，试验和有限元结果(Nu)与CECS410计算结果(Nu,CECS)的比值为纵坐标，绘制图19，比值的平均值和标准差按截面分类后列于表6。
![]()
图 19 有限元和试验结果与CECS410计算结果对比Figure 19. Comparison of CECS410 design formulas with test and FE results表 6 CECS410和建议公式的比对结果Table 6. Comparison between CECS410 and proposed formula截面类型 构件个数 Nu /Nu,CECS Nu /Nu,prop 试验 有限元 平均值 标准差 平均值 标准差 \overline{\lambda}_{\mathrm{p}} ≤0.62 9 113 1.158 0.096 1.004 0.020 \overline{\lambda}_{\mathrm{p}}>0.62 12 94 1.081 0.055 1.002 0.039 全截面 21 207 1.122 0.088 1.003 0.031 CECS410计算公式对区分紧凑截面和薄柔截面的柔度系数限值为{\overline \lambda _{\text{p}}}=0.54，但分析图16可知，针对激光焊接T形截面取{\overline \lambda _{\text{p}}}=0.62更为准确。图19表明，当构件全截面柔度系数{\overline \lambda _{\text{p}}}<0.62(紧凑截面)时，设计公式由于忽略了不锈钢材料应变硬化效应的有利影响，计算结果偏于保守；当构件柔度系数{\overline \lambda _{\text{p}}}>1.0(薄柔截面)时，焊接残余应力对截面承载力影响增大，传统焊接的有效宽度折减系数不适合激光焊接，低估了构件的截面承载力。试验和有限元结果与规范计算结果比值的平均值为1.122，标准差为0.088，表明CECS410设计公式在预测激光焊接不锈钢T形截面轴压构件截面承载力时偏于保守。
4.3 截面承载力设计公式修正
为提高CECS410针对激光焊接T形截面轴压构件截面承载力的设计效率，本文根据图16中截面承载力与全截面柔度系数{\overline \lambda _{\text{p}}}的函数关系，对设计公式进行修正。对于{\overline \lambda _{\text{p}}}<0.62的紧凑截面，引入应变硬化系数{\beta _{\text{n}}}来考虑材料应变硬化效应的有利影响，通过与柔度系数{\overline \lambda _{\text{p}}}的函数关系，在构件全截面名义屈服的基础上加以提高，可用式(6)较好拟合。为防止构件应变硬化过度发展而引起过大变形，结合实用性和图16中截面承载力分布情况，对应变硬化系数设置上限，即{\beta _{\text{n}}}≤1.4。本文所研究构件的轴向应变值均未超过欧洲规范[20]规定的0.1 {\varepsilon _{\text{u}}} 。
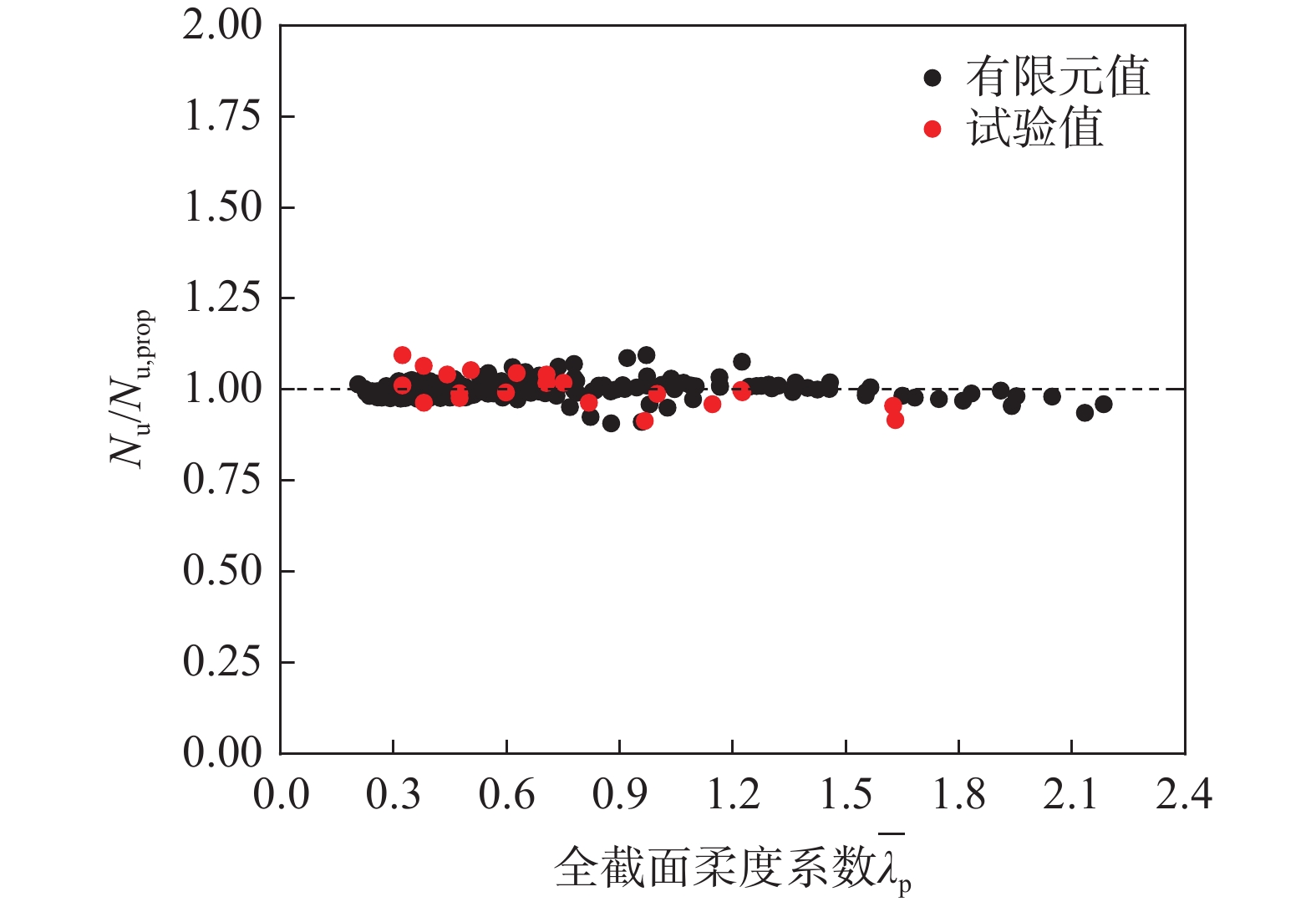
{\beta _{\text{n}}} = \frac{1}{{0.87\sqrt {{{\overline \lambda }_{\text{p}}}} + 0.31}} (6) 对于{\overline \lambda _{\text{p}}}>0.62的薄柔构件，传统焊接的有效宽度折减系数低估了构件的截面承载力，本文在原计算公式函数形式和{\overline \lambda _{\text{p}}}分界不变的情况下，根据图16对{\alpha _1} \sim {\alpha _6}进行了重新拟合，修正后的计算系数列于表5。综上，本文建议的激光焊接不锈钢T形截面轴压构件截面承载力设计公式见式(7)：
\frac{N}{{{\beta _{\text{n}}}{A_{{\text{en}}}}}} {\leqslant} {f_{\text{y}}} (7) 修正后设计公式计算结果(Nu,prop)与试验和有限元模拟结果(Nu)的对比如图20所示，表6按截面类型列出了修正前、后设计公式计算结果与试验和有限元结果比值的平均值和标准差，试验和有限元结果与建议公式计算结果比值的平均值为1.003，标准差为0.031；根据我国《建筑结构可靠性设计统一标准》[31]对设计公式可靠性进行计算，建议公式的可靠指标β=4.92，满足一级延性破坏可靠指标为3.7的要求；激光焊接不锈钢T形截面构件截面承载力建议设计公式的准确性和安全性得到了验证。
![]()
图 20 有限元和试验结果与修正后设计公式计算结果对比Figure 20. Comparison of proposed design formulas with test and FE results因不同牌号不锈钢材料本构模型差距较大，本文建议公式基于S30408奥氏体不锈钢提出；针对奥氏体不锈钢，可通过修改名义屈服强度考虑力学性能指标的不同，建议公式仍然适用。针对铁素体和双相不锈钢，需开展相关研究进一步完善设计公式。
5 结论
本文在激光焊接不锈钢T形截面构件残余应力、轴压试验基础上，验证有限元模拟加载的准确性，通过有限元模拟扩充截面承载力数据并分析激光焊接残余应力对截面承载力的影响，评估及改进CECS410中构件轴压截面承载力设计公式，得出以下结论：
(1) 提出了激光焊接奥氏体不锈钢T形截面构件的纵向残余应力简化分布模型。
(2) 激光焊接残余应力对奥氏体不锈钢T形截面轴压构件截面承载力的降低程度，随宽厚比的增大而增大，对紧凑截面不足1%，对薄柔截面不超过3%。
(3) CECS410中截面承载力设计公式，因未考虑不锈钢材料的应变硬化效应以及有效宽度折减系数的不适用性，低估了构件的截面承载力。
(4)基于CECS410设计公式，引入应变硬化系数和修正有效宽度折减系数，得到的建议公式经可靠性指标验证，能够安全、准确地预测激光焊接奥氏体不锈钢T形截面轴压构件的截面承载力。
-
![]()
图 2 残余应力试件取材位置和条带切割示意 /mm
Figure 2. Selection position and strip cutting diagram of residual stress specimens
![]()
图 7 实测残余应力与预测模型的比较
Figure 7. Comparison of measured residual stresses and predictive models
![]()
图 13 试验与有限元模拟荷载-轴向位移曲线对比
Figure 13. Comparison of load-axial displacement curves between test and FE simulation
![]()
图 15 典型短柱试件试验与有限元模型破坏模态对比
Figure 15. Comparison of failure modes for typical stub column specimens between test and FE simulation
![]()
图 16 截面承载力随全截面柔度系数分布
Figure 16. Distribution of cross-sectional resistance with full section slenderness coefficient
![]()
图 18 CECS410受压板件宽厚比限值评估
Figure 18. Assessment of CECS410 width-to-thickness ratios for compression elements
![]()
图 19 有限元和试验结果与CECS410计算结果对比
Figure 19. Comparison of CECS410 design formulas with test and FE results
![]()
图 20 有限元和试验结果与修正后设计公式计算结果对比
Figure 20. Comparison of proposed design formulas with test and FE results
表 1 短柱试件实测几何尺寸
Table 1 Measured geometric dimensions of stub column specimens
试件编号 截面高度
h/mm截面宽度
bf/mm板件厚度
t/mm试件长度
L/mm形心位置
x0/mm腹板翼缘宽厚比及板件类型 试件截面类型 翼缘宽厚比b1/tf 翼缘类型 腹板宽厚比hw/tw 腹板类型 T60-60-3 62.42 59.81 2.89 179.49 17.2 9.85 紧凑型 20.67 薄柔型 薄柔截面 T60-60-5 64.49 60.89 4.74 179.42 18.6 5.92 紧凑型 12.63 薄柔型 薄柔截面 T60-60-8-1 67.39 60.69 7.62 179.41 20.7 3.48 紧凑型 7.85 紧凑型 紧凑截面 T60-60-8-2 67.32 60.73 7.63 179.41 20.7 3.48 紧凑型 7.83 紧凑型 紧凑截面 T60-90-3 62.52 89.59 2.89 269.42 14.0 14.95 薄柔型 20.71 薄柔型 薄柔截面 T60-90-5 64.53 89.58 4.73 269.48 15.5 8.95 紧凑型 12.67 薄柔型 薄柔截面 T60-90-8-1 67.82 89.52 7.64 269.43 17.3 5.38 紧凑型 7.90 紧凑型 紧凑截面 T60-90-8-2 67.84 89.54 7.64 269.47 17.3 5.37 紧凑型 7.88 紧凑型 紧凑截面 T60-120-3 62.68 119.83 2.89 359.12 11.9 20.30 薄柔型 20.68 薄柔型 薄柔截面 T60-120-5-1 64.42 119.88 4.74 359.52 13.2 12.17 薄柔型 12.60 薄柔型 薄柔截面 T60-120-5-2 64.43 119.77 4.73 359.48 13.2 12.16 薄柔型 12.62 薄柔型 薄柔截面 T60-120-8 67.11 119.76 7.63 359.37 15.1 7.35 紧凑型 7.83 紧凑型 紧凑截面 T90-90-3-1 92.72 89.63 2.87 269.82 24.7 15.06 薄柔型 31.41 薄柔型 薄柔截面 T90-90-3-2 92.68 89.62 2.88 269.77 24.7 15.04 薄柔型 31.17 薄柔型 薄柔截面 T90-90-5 94.33 89.61 4.73 269.92 26.0 8.97 紧凑型 18.95 薄柔型 薄柔截面 T90-90-8-1 97.48 89.82 7.63 269.88 28.2 5.40 紧凑型 11.82 薄柔型 薄柔截面 T90-90-8-2 97.53 89.83 7.62 269.87 28.2 5.40 紧凑型 11.82 薄柔型 薄柔截面 T120-120-3-1 122.68 119.70 2.88 359.51 32.2 20.28 薄柔型 41.73 薄柔型 薄柔截面 T120-120-3-2 122.73 119.62 2.90 359.48 32.2 20.19 薄柔型 41.32 薄柔型 薄柔截面 T120-120-5 124.22 119.48 4.73 359.86 33.5 12.15 薄柔型 25.22 薄柔型 薄柔截面 T120-120-8 127.42 119.88 7.63 359.71 35.7 7.36 紧凑型 15.72 薄柔型 薄柔截面 
下载: 导出CSV
表 2 S30408不锈钢材料性能参数
Table 2 Material properties of S30408 stainless steel plates
厚度 E/GPa \sigma_{0.2} /MPa \sigma_{{\mathrm{u}}} /MPa \varepsilon_{{\mathrm{f}}} /(%) n m T3 191.8 274 754 62 6.33 2.02 T5 192.3 286 774 59 6.81 2.04 T8 186.8 281 715 62 7.58 2.09 注：E为弹性模量；σ0.2为0.2%塑性应变对应的应力(名义屈服强度)；σu为极限抗拉强度；εf为断后伸长率；n、m为ARRAYAGO[28]不锈钢本构模型相关参数。
下载: 导出CSV
表 3 建议残余应力模型参数
Table 3 Proposed model factor for residual stress
模型参数 \sigma_{ {\mathrm{r, ft}}} = \sigma_{\text {r,wt1}} \boldsymbol{\sigma}_{\text {r,wt2}} a b c d 参数值 0.5 \sigma_{\text {0.2}} 0.1 \sigma_{\text {0.2}} 0.1bf 0.1bf 0.05hw 0.1hw 注：1) \sigma_{ {\mathrm{r, fc}}} , \sigma_{ {\mathrm{r, wc}}} 由截面应力自平衡得到；2) f和w分别为翼缘和腹板；3) t和c分别为拉力和压力。
下载: 导出CSV
表 4 短柱试件轴压试验结果与有限元模拟结果比较
Table 4 Comparison between stub column axial compression test and FE results
试件编号 \overline{\lambda}_{\mathrm{p}} 试验结果 模型不同缺陷幅值对应的Nu,FE/Nu,test \omega_0 /mm \omega_0 /b Nu,test/kN {\varDelta}_{\text {u,test}} /mm \omega_0 b /50 b /100 b /200 T60-60-3 0.82 0.04 1/1500 79.03 0.76 1.02 0.98 0.99 1.00 T60-60-5 0.51 0.05 1/1200 182.06 1.74 1.02 0.97 0.98 0.99 T60-60-8-1 0.32 0.09 1/666 350.35 5.51 1.02 0.95 0.96 0.98 T60-60-8-2 0.32 0.05 1/1200 324.17 4.32 0.99 0.96 0.97 0.99 T60-90-3 0.97 0.03 1/1500 83.22 1.35 1.00 0.98 0.99 1.00 T60-90-5 0.60 0.03 1/2000 200.48 1.62 1.00 0.97 0.98 1.00 T60-90-8-1 0.38 0.10 1/600 403.38 5.88 1.01 0.96 0.96 0.97 T60-90-8-2 0.38 0.04 1/1500 365.62 3.73 0.98 0.97 0.97 0.98 T60-120-3 1.15 0.06 1/1000 92.52 1.01 0.99 0.98 0.98 0.99 T60-120-5-1 0.71 0.03 1/2000 230.87 1.62 0.99 0.98 0.98 0.99 T60-120-5-2 0.71 0.07 1/857 225.46 1.79 1.00 0.98 0.99 1.00 T60-120-8 0.44 0.11 1/545 449.43 3.80 0.99 0.97 0.99 0.99 T90-90-3-1 1.22 0.07 1/1286 91.91 1.02 1.02 1.00 1.01 1.02 T90-90-3-2 1.22 0.07 1/1286 91.74 1.03 1.02 1.00 1.01 1.02 T90-90-5 0.75 0.03 1/3000 217.19 1.35 0.99 0.96 0.98 0.99 T90-90-8-1 0.48 0.06 1/1500 418.02 1.99 0.98 0.97 0.97 0.98 T90-90-8-2 0.48 0.03 1/3000 412.91 2.09 0.98 0.97 0.98 0.98 T120-120-3-1 1.63 0.09 1/1333 102.08 1.25 0.99 0.97 0.98 0.99 T120-120-3-2 1.63 0.08 1/1500 98.45 1.38 0.99 0.97 0.98 0.99 T120-120-5 1.00 0.05 1/2400 229.12 1.80 0.99 0.97 0.98 0.99 T120-120-8 0.63 0.06 1/2000 530.38 2.11 1.01 0.99 1.00 1.01 平均值 1.01 0.97 0.98 0.99 标准差 0.01 0.01 0.01 0.01 注： \overline{\lambda}_{\mathrm{p}} 为试件全截面柔度系数； \omega_0 为实测试件初始几何缺陷幅值。
下载: 导出CSV
表 5 焊接构件有效宽度折减系数
Table 5 Effective width reduction factor for welded components
参数来源 \alpha_{1} \alpha_{2} \alpha_3 \alpha_{4} \alpha_5 \alpha_6 CECS410 1.84 −1.14 3.15 −1.72 0.086 0.62 建议公式 1.97 −1.24 2.53 −1.17 0.28 0.44
下载: 导出CSV
表 6 CECS410和建议公式的比对结果
Table 6 Comparison between CECS410 and proposed formula
截面类型 构件个数 Nu /Nu,CECS Nu /Nu,prop 试验 有限元 平均值 标准差 平均值 标准差 \overline{\lambda}_{\mathrm{p}} ≤0.62 9 113 1.158 0.096 1.004 0.020 \overline{\lambda}_{\mathrm{p}}>0.62 12 94 1.081 0.055 1.002 0.039 全截面 21 207 1.122 0.088 1.003 0.031
下载: 导出CSV
-
[1] 杨松, 郑山锁, 田忠祥, 等. 锈蚀Q345B钢力学特性试验及循环本构模型研究 [J]. 工程力学, doi: 10.6052/j.issn.1000-4750.2022.11.0971. YANG Song, ZHENG Shansuo, TIAN Zhongxiang, et al. Mechanical properties test and cyclic constitutive model of corroded Q345B steel [J]. Engineering Mechanics, doi: 10.6052/j.issn.1000-4750.2022.11.0971. (in Chinese)
[2] 彭建新, 赵洋, 王贤基, 等. 锈蚀Q345C钢材疲劳性能试验研究及数值模拟 [J]. 工程力学, doi: 10.6052/j.issn.1000-4750.2022.10.0866. PENG Jianxin, ZHAO Yang, WANG Xianji, et al. Experimental study and numerical simulation on fatigue properties of corroded Q345C steel [J]. Engineering Mechanics, doi: 10.6052/j.issn.1000-4750.2022.10.0866. (in Chinese)
[3] GARDNER L. Stability and design of stainless steel structures-Review and outlook [J]. Thin-Walled Structures, 2019, 141: 208 − 216. doi: 10.1016/j.tws.2019.04.019
[4] NING K Y, YANG L, WANG J, et al. Experimental and numerical study of hot-rolled duplex stainless steel CHS columns [J]. Journal of Constructional Steel Research, 2021, 180: 106579. doi: 10.1016/j.jcsr.2021.106579
[5] 邢哲, 毋凯冬, 张颖, 等. 高温下焊接不锈钢轴心受压构件稳定性能研究 [J]. 工程力学, doi: 10.6052/j.issn.1000-4750.2022.11.0955. XING Zhe, WU Kaidong, ZHANG Ying, et al. Stability of welded stainless steel axial compressive members at elevated temperatures [J]. Engineering Mechanics, doi: 10.6052/j.issn.1000-4750.2022.11.0955. (in Chinese)
[6] 张浩, 袁森, 苏明周, 等. 拉剪复合作用下不锈钢槽式预埋组件力学性能 [J]. 工程力学, doi: 10.6052/j.issn.1000-4750.2023.03.0194. ZHANG Hao, YUAN Sen, SU Mingzhou, et al. Mechanical behaviors of stainless steel anchor channel assemblies under combined tension and shear [J]. Engineering Mechanics, doi: 10.6052/j.issn.1000-4750.2023.03.0194. (in Chinese)
[7] 宁克洋, 杨璐, 张允, 等. 奥氏体型不锈钢受弯构件截面分类研究 [J]. 工程力学, 2023, 40(9): 98 − 107. doi: 10.6052/j.issn.1000-4750.2022.01.0037 NING Keyang, YANG Lu, ZHANG Yun, et al. Research on section classification of austenitic stainless steel flexural members [J]. Engineering Mechanics, 2023, 40(9): 98 − 107. (in Chinese) doi: 10.6052/j.issn.1000-4750.2022.01.0037
[8] RAGAVENDRAN M, VASUDEVAN M. Effect of laser and hybrid laser welding processes on the residual stresses and distortion in AISI type 316L(N) stainless steel weld joints [J]. Metallurgical and Materials Transactions B, 2021, 52(4): 2582 − 2603. doi: 10.1007/s11663-021-02202-w
[9] YANG F, XIA G J, GUO X, et al. Research progress of laser welding under subatmospheric pressure [J]. The International Journal of Advanced Manufacturing Technology, 2021, 116(3/4): 803 − 820.
[10] GARDNER L, BU Y D, THEOFANOUS M. Laser-welded stainless steel I-sections: Residual stress measurements and column buckling tests [J]. Engineering Structures, 2016, 127: 536 − 548. doi: 10.1016/j.engstruct.2016.08.057
[11] FILIPOVIĆ A, DOBRIĆ J, BUĐEVAC D, et al. Experimental study of laser-welded stainless steel angle columns [J]. Thin-Walled Structures, 2021, 164: 107777. doi: 10.1016/j.tws.2021.107777
[12] RAN H D, CHEN Z P, MA Y M. Experimental and numerical studies of laser-welded slender stainless steel I-section columns [J]. Thin-Walled Structures, 2022, 171: 108832. doi: 10.1016/j.tws.2021.108832
[13] RAN H D, CHEN Z P, MA Y M, et al. Local stability of laser-welded stainless steel slender I-sections under combined loading [J]. Journal of Constructional Steel Research, 2023, 200: 107649. doi: 10.1016/j.jcsr.2022.107649
[14] BU Y, GARDNER L. Local stability of laser-welded stainless steel I-sections in bending [J]. Journal of Constructional Steel Research, 2018, 148: 49 − 64. doi: 10.1016/j.jcsr.2018.05.010
[15] LIANG Y T, ZHAO O, LONG Y L, et al. Experimental and numerical studies of laser-welded stainless steel channel sections under combined compression and major axis bending moment [J]. Thin-Walled Structures, 2020, 157: 107035. doi: 10.1016/j.tws.2020.107035
[16] RAN H D, CHEN Z P, MA Y M, et al. Experimental and numerical study of laser-welded stainless steel slender I-section beam-columns [J]. Engineering Structures, 2023, 286: 116128. doi: 10.1016/j.engstruct.2023.116128
[17] RAN H D, TANG Z L, WANG Y B, et al. Testing, modelling and design of laser-welded stainless steel slender I-section beam-column members under combined compression and major-axis bending [J]. Thin-Walled Structures, 2024, 203: 112238. doi: 10.1016/j.tws.2024.112238
[18] BU Y D, GARDNER L. Laser-welded stainless steel I-section beam-columns: Testing, simulation and design [J]. Engineering Structures, 2019, 179: 23 − 36. doi: 10.1016/j.engstruct.2018.09.075
[19] THEOFANOUS M, LIEW A, GARDNER L. Experimental study of stainless steel angles and channels in bending [J]. Structures, 2015, 4: 80 − 90. doi: 10.1016/j.istruc.2015.10.004
[20] EN 1993-1-4, Eurocode 3: Design of steel structures: Part 1-4: General rules: Supplementary rules for stainless steels [S]. London: BSI, 2006.
[21] ANSI/AISC 370-21, Specification for structural stainless steel buildings [S]. Chicago: AISC, 2021.
[22] GARDNER L, YUN X, WALPORT F. The continuous strength method–Review and outlook [J]. Engineering Structures, 2023, 275: 114924. doi: 10.1016/j.engstruct.2022.114924
[23] CECS 410−2015, 不锈钢结构技术规程 [S]. 北京: 中国计划出版社, 2015. CECS 410−2015, Technical specification for stainless steel structures [S]. Beijing: China Planning Press, 2015. (in Chinese)
[24] RAN H D, MA J, CHEN X R, et al. Local stability of laser-welded stainless-steel T-section stub columns [J]. Journal of Structural Engineering, 2024, 150(7): 04024062. doi: 10.1061/JSENDH.STENG-13323
[25] ZIEMIAN R D. Guide to stability design criteria for metal structures [M]. Hoboken: NJ: Wiley, 2010: 471 − 473.
[26] GB/T 228.1−2021, 金属材料 拉伸试验 第1部分: 室温试验方法[S]. 北京: 中国标准出版社, 2021. GB/T 228.1−2021, Metallic materials-Tensile testing-Part 1: Method of test at room temperature [S]. Beijing: Standards Press of China, 2021. (in Chinese)
[27] GB/T 2975−2018, 钢及钢产品 力学性能试验取样位置及试样制备 [S]. 北京: 中国标准出版社, 2018. GB/T 2975−2018, Steel and steel products-Location and preparation of samples and test pieces for mechanical testing [S]. Beijing: Standards Press of China, 2018. (in Chinese)
[28] ARRAYAGO I, REAL E, GARDNER L. Description of stress-strain curves for stainless steel alloys [J]. Materials & Design, 2015, 87: 540 − 552.
[29] GB 50205−2020, 钢结构工程施工质量验收标准 [S]. 北京: 中国计划出版社, 2020. GB 50205−2020, Standard for acceptance of construction quality of steel structures [S]. Beijing: China Planning Press, 2020. (in Chinese)
[30] SCHAFER B W, ÁDÁNY S. Buckling analysis of cold-formed steel members using CUFSM: Conventional and constrained finite strip methods [C]// The 18th International Specialty Conference on Cold-Formed Steel Structures. Orlando, 2006: 39 − 54. Rolla, MI: Missouri Univ. of Science and Technology.
[31] GB 50068−2018, 建筑结构可靠性设计统一标准 [S]. 北京: 中国建筑工业出版社, 2018. GB 50068−2018, Unified standard for reliability design of building structures [S]. Beijing: China Architecture & Building Press, 2018. (in Chinese)
计量
- 文章访问数: 49
- HTML全文浏览量: 13
- PDF下载量: 7
