串列结构在实际工程中被广泛应用，如冷却塔群、海洋立管和桥梁索塔等。轻质高强材料的应用使得结构向着高柔、低阻尼方向发展，风荷载成为影响结构安全的关键因素^{[1 − 4]}。同时，由于结构间复杂的干扰作用，串列结构会产生与单体结构不同的风致响应^[5]，严重时甚至会造成结构破坏，如英国渡桥电厂冷却塔倒塌及深圳赛格大厦发生风致振动^{[6 − 8]}。建筑物截面沿高度逐渐变窄即锥度化修正(如图1(a)所示)，能够有效降低结构的横风向荷载和响应^{[9 − 10]}，已被广泛应用于超高层建筑、风机塔筒和H形桥塔等结构。均匀来流下的串列双锥形方柱是群体建筑的一种简化模型^[11]，探究串列双锥形方柱气动干扰效应和流场机理对群体结构的抗风设计具有重要参考意义。

串列双方柱气动干扰机理复杂，对间距比G/D^{[12 − 16]}(G为柱心间距，D为方柱边长，如图1(b)所示)和来流风向^[17]十分敏感。SAKAMOTO等^[12]采用风洞试验对不同间距比串列双方柱进行研究，并将气动力发生突变的间距比被称为临界间距比。LIU等^[13]、YEN等^[14]通过风洞试验探究了间距比对串列双方柱气动特性和流场的影响，根据间距比将流场划分为：单一钝体、剪切层再附及双涡脱流态。SOHANKAR^[16]采用大涡模拟方法对不同间距比和雷诺数下的串列双方柱进行二维和三维数值模拟，同样观察到了上述三种流态，同时发现二维数值模拟结果存在较大误差。DU等^[12]采用大涡模拟方法对Re=8×10⁴的串列双方柱进行研究，探究了双方柱气动力特性和极值风压随间距比的变化规律。

图  1  计算模型示意图

Figure  1.  Schematic diagram of calculation model

下载: 全尺寸图片 幻灯片

除串列间距比外，来流风向角α(如图1(b)所示)是影响双方柱流动特性的另一个关键参数。YOON等^[18]对不同风向下单方柱进行数值模拟研究，发现风向角显著影响流体分离位置，并决定了方柱周围流场形态。YEN等^[19]和SOHANKAR等^[20]探究了单方柱流场形态随风向角(0°~45°)的变化情况，将流场形态划分为3种流态：前角分离流态、分离泡流态和附着流流态。DU等^[21]进行了高雷诺数下串列双方柱风洞试验，探究了间距比和风向角对双方柱气动力特性的影响，根据平均气动力系数的不同将双方柱绕流问题分为小间距比(G/D < 1.5)、中等间距比(1.5 ≤ G/D ≤ 3)和大间距比(3 < G/D ≤ 5)。由于双方柱均为钝体结构，棱角较为分明，因此雷诺数对双方柱气动力和流场的影响较小。另外，BAI和ALAM^[22]的研究发现，Re = 2×10³时单方柱的气动力(平均阻力系数和斯托罗哈数)和流场特征(旋涡脱落长度和尾流宽度)与高雷诺数(Re < 10⁷)相似。因此，为在有限的计算资源下获得风向对串列双方柱的气动力和流场的影响，选择了Re = 2×10³进行研究。同时，实际工程中H形桥塔串列间距多为4D左右，故选取间距比G/D = 4进行研究。另外，本文针对串列布置形式下的双方柱进行研究，因此风向角选为0°~45°。

KIM等^{[23 − 24]}对不同锥度下单体超高层建筑进行风洞试验，发现锥度化措施能够有效消减结构的横风向风荷载。DENG等^[25]研究发现，锥度化措施不仅能增加漩涡脱落频率，同时能减少漩涡脱落能量。SHARMA等^{[26 − 27]}采用DES(detached-eddy simulation)方法对锥度为5%、10%和15%的单个超高层建筑进行研究，发现结构气动力和表面风压系数随锥度的增大降低。LI等^{[28 − 29]}对不同锥度下(5%、10%、15% 、20%)的CAARC标准超高层建筑进行三维大涡模拟和风洞试验，讨论并比较了不同锥度模型的风压系数和气动力系数等参数的变化。在工程实际中，H形桥塔和高层建筑等串列钝体结构的锥度往往在5%左右。另外，根据众多学者对锥度的研究^{[28 − 30]}可以看出，与标准方形建筑相比，当ξ = 5%时，结构的气动特性和流场发生了显著变化，因此选择5%的锥度比进行研究可以更好地为实际工程提供理论参考。因此，本研究将选取锥度为5%的串列双方柱进行深入研究。

综上所述，以往关于串列方柱干扰效应的研究多集中于串列间距比的影响，未考虑锥度的变化。而关于锥度对方柱风荷载的研究，多集中于单体，并未考虑柱体间的干扰效应。因此，本研究采用基于CFD的大涡数值模拟方法，对雷诺数Re为2.0×10³的不同风向角下串列双方柱进行研究，其中间距比G/D为4，锥度ξ为0%和5%，风向角α分别选取0°、5°、10°、15°、30°和45°；系统地研究了风向角和锥度化措施对结构气动力和风压特性的影响，并从流场角度揭示了气动特性变化原因；最后，建立了风向角与气动特性间的数学关系式，为串列结构的设计和建造提供理论参考。

1   数值方法和模拟设置

1.1   控制方程和数值格式

大涡模拟采用空间滤波技术，将湍流运动分为大涡和小涡，其中大涡由过滤后的Navier-Stokes (N-S)方程直接求解，而小涡则由亚格子应力模型(sub-grid scale，SGS)模拟^{[31 − 33]}。滤波后的不可压缩N-S方程如下：

式中：${\widetilde u_i}$为过滤后的速度分量；$\widetilde p$为滤波后压力；${\widetilde S_{ij}} = \dfrac{1}{2}\left( {\dfrac{{\partial \widetilde {{u_i}}}}{{\partial {x_j}}} + \dfrac{{\partial \widetilde {{u_j}}}}{{\partial {x_i}}}} \right)$为过滤后的应变率张量；$\rho$和$\nu$分别为流体密度和运动粘性系数；${\tau _{ij}}$为亚格子尺度雷诺应力(SGS Reynolds stress)。亚格子应力表达式如下：

式中，${\nu _{{\mathrm{sgs}}}}$为亚格子尺度湍流黏度系数。选择壁面自适应局部涡流粘度(WALE)模型作为亚格子模型，以准确模拟层流到湍流的过渡^{[34 − 35]}，其${\nu _{{\mathrm{sgs}}}}$表达式如下：

式中，${k_{{\mathrm{sgs}}}}$为亚格子模型湍动能，表达式如下：

式中：模型系数${C_{\mathrm{k}}}$和${C_{\mathrm{w}}}$为常数，分别为0.094和0.325；此外， S为应变率张量，$\tilde{S}_{ij}^{\text{d}}$是应变率张量S_ij的偏斜部分，$\tilde{S}_{ji}^{\text{d}}$是应变率张量S_ji的偏斜部分。 $\widetilde \varDelta = \sqrt[3]{{\varDelta x\varDelta y\varDelta {\textit{z}}}}$表示过滤后的网格尺度。最终的${\nu _{{\mathrm{sgs}}}}$表达式如式(6)：

整个计算域采用有限体积法进行离散，速度和压力项采用具有二阶精度的离散格式，时间项采用二阶隐式离散格式，梯度项采用高斯线性中心差分格式，散度项采用高斯二阶线性格式，残差设为1×10⁻⁶。基于OpenFOAM^©开源计算平台，并采用瞬态不可压缩pimpleFoam求解器(PIMPLE算法，PISO和SIMPLE算法的组合)对雷诺数Re为2.0×10³的不同风向角下串列双方柱进行研究。无量纲时间步长$\varDelta {t^*} = \varDelta {t}{{{U_0}} /D}$设为0.0025，采样时长不少于30个漩涡脱落周期^[36]。

1.2   计算域和网格

如图1(a)所示，双方柱采取串列布置方式，方柱边长为D，柱心间距比G/D = 4。上游方柱(UC)与下游方柱(DC)的相对位置不随α变化，α选取0°、5°、10°、15°、30°和45°。如图1(b)所示，方柱锥度$\xi = {{({D_1} - {D_2})} / H}$，其中，H为方柱高度，D₁和D₂分别为方柱底部和顶部边长。选取0%和5%两种锥度进行数值模拟研究。为使流动充分发展，采用直径为20D的圆形计算域。展向高度H设置为4D以更好的模拟三维特性^[37]，计算域如图2所示。阻塞率在2.5%~7.1%，小于RODI^[38]的建议值(7.7%)。

图  2  计算域和边界条件

Figure  2.  Computational domain and boundary conditions

下载: 全尺寸图片 幻灯片

入口设置为均匀流速度入口，顺流向速度u = U_∞ = 1 m/s，横向速度v = 展向速度w = 0，出口为压力出口边界。展向采用周期性边界条件(Cyclic)。当方柱采取锥度化措施修正时，由于锥形方柱的上下面大小不一致，导致展向的两个面不对称，而Cyclic边界条件要求展向两个面是完全一致的。因此，Cyclic边界条件不适用于锥度化双方柱的展向边界。滑移边界(Slip)允许气流在表面上的滑移，能够最大限度的削弱方柱顶端三维效应的影响。因此，当双方柱采取锥度化措施修正时，展向采用Slip边界。方柱表面边界条件定义为无滑移壁面边界(No-slip)。运动粘度系数v = 5×10^–4 m²/s，方柱特征长度D = 1 m，对应雷诺数Re = U_∞D/v ≈ 2×10³。

采用O形分块的结构化网格进行划分，如图3所示。壁面首层网格高度按$0.1/\sqrt {{Re} }$^{[39 − 41]}经验公式计算，取值0.0023D，保证近壁面第一层网格的y⁺值小于1，远离柱体的区域径向增长率选为1.10。柱体近壁面径向增长率选为1.05^[42]。周向划分200个网格并在柱体角部进行加密处理，柱体角部第一个网格的长度为0.01D，展向均匀划分40个网格，每层网格宽度为0.1D。由此计算得到的x⁺值约为4.3，z⁺值约为43。

图  3  整体和局部网格示意图

Figure  3.  Mesh distributions of the numerical model overall mesh and local grids

下载: 全尺寸图片 幻灯片

2   数值验证

2.1   网格无关性验证

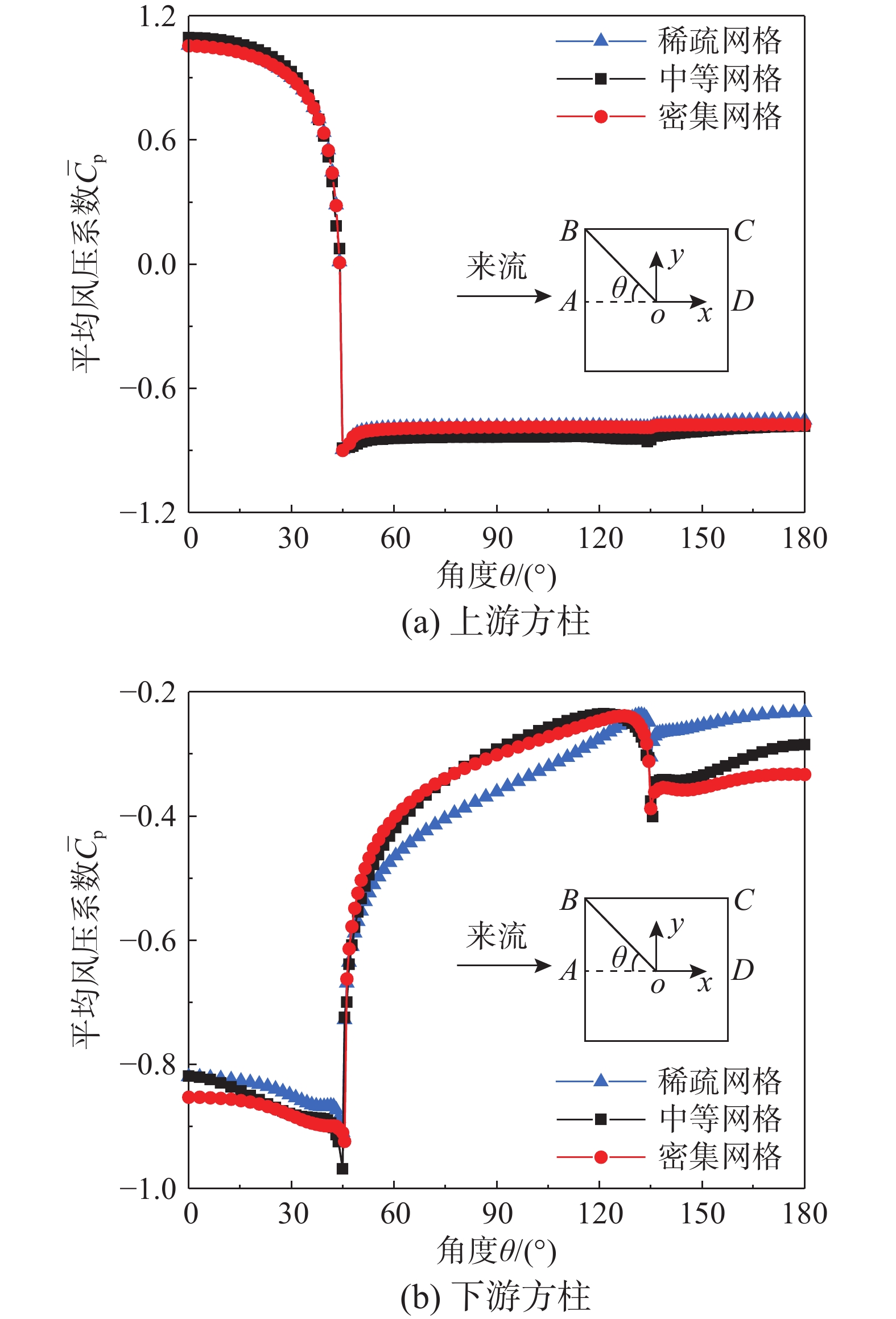
采用稀疏、中等和稠密3种网格对风向角为0°时的标准串列双方柱网格进行无关性验证。其中稀疏网格的最小网格增长率为1.10，网格总量为134万。中等网格的最小网格增长率为1.05，网格总量为223万。稠密网格的最小网格增长率为1.01，网格总量为320万。对比参数包括平均阻力系数${\overline C_{\mathrm{D}}}$、脉动阻力系数${C_{\mathrm{D}}^\prime}$、脉动升力系数${C_{\mathrm{L}}^\prime}$、斯托罗哈数St和平均风压系数。气动参数定义如下：${{{C_{\mathrm{D}}} = 2{F_{\mathrm{D}}}} / {{\rho _\infty }}}U_\infty ^2DL$，${{{C_{\mathrm{L}}} = 2{F_{\mathrm{L}}}} /{{\rho _\infty }}}U_\infty ^2DL$， St = f_vD/U，其中F_D和F_L分别为方柱所受阻力和升力，D和L分别表示方柱的长度和高度，f_v为漩涡脱落频率^[43]。平均风压系数的计算公式为${{\overline C }_{\mathrm{p}}} = 2( {\overline P - {P_\infty }} ) / {{\rho _\infty }}U_\infty ^2$，其中$\overline P$为方柱表面平均风压，${P_\infty }$为入口参考风压^[44]。以稠密网格的平均阻力为基准，计算稀疏和稠密网格的相对误差，上游方柱的气动力验证结果见表1，下游方柱的气动力验证结果见表2。平均风压系数的验证结果如图4所示。可以看出，稀疏网格与稠密网格对上游方柱的模拟结果较为吻合，但下游方柱气动力结果相差较大，平均阻力系数相对误差高达22.03%，下游方柱的平均风压系数也相差较大；而中等网格与稠密网格在上下游的吻合程度均较好，下游方柱的阻力系数相对误差仅为2.09%，平均风压系数分布曲线基本重合。因此，在保证计算精度的前提下可以认为，中等网格足以满足精度要求。

表  1  上游方柱平均积分分量对比表

Table  1.  Comparison of average integral components of upstream square cylinder

网格类型	${\overline C_{\mathrm{D} }}$	${C_{\mathrm{D} }^\prime}$	${C_{\mathrm{L} }^\prime}$	斯托罗哈数St	平均阻力相对误差/(%)
稀疏	1.6466	0.0071	0.0240	0.1200	3.11
中等	1.6040	0.0105	0.0360	0.1590	0.45
稠密	1.5968	0.0103	0.0327	0.1570	0.00

下载: 导出CSV 

| 显示表格

表  2  下游方柱平均积分分量对比表

Table  2.  Comparison of average integral components of downstream square cylinder

网格类型	${\overline C_{\mathrm{D} }}$	${C_{\mathrm{D} }^\prime}$	${C_{\mathrm{L} }^\prime}$	斯托罗哈数St	平均阻力相对误差/(%)
稀疏	−0.5240	0.1102	0.4365	0.1200	22.03
中等	−0.6580	0.1117	0.4316	0.1590	2.09
稠密	−0.6721	0.1135	0.4385	0.1570	0.00

下载: 导出CSV 

| 显示表格

图  4  不同网格密度下的双方柱平均风压系数

Figure  4.  Mean wind pressure coefficient on two tandem square cylinders under different grid densities

下载: 全尺寸图片 幻灯片

2.2   数值结果验证

以Re = 2.2×10⁴单方柱模型为例，采用同样的网格划分及数值设置，将模拟结果与前人试验进行对比。如表3所示，模拟结果与前人试验吻合较好，部分结果由于雷诺数的不同有较小差异。

表  3  单方柱部分平均积分分量对比表

Table  3.  Comparison of mean integral components of a square cylinder Part

	方法	雷诺数Re	${\overline C_{\mathrm{D} }}$	${C_{\mathrm{D} }^\prime}$	${C_{\mathrm{L} }^\prime}$	斯托罗哈数St
NORBERG[45]	Exp	1.30×104	2.16	−	−	0.13
LYN等[46]	Exp	2.14×104	2.10	−	−	0.13
LUO等[47]	Exp	3.40×104	2.21	0.19	1.26	0.13
杜晓庆等[37]	LES	8.00×104	2.00	0.22	1.36	0.12
SOHANKAR等[48]	LES	2.20×104	2.32	0.20	1.54	0.13
CAO和TAMURA[49]	LES	2.20×104	2.21	0.22	1.51	0.13
本研究	LES	2.20×104	2.15	0.19	1.55	0.12

下载: 导出CSV 

| 显示表格

双方柱的气动特性与单方柱差异较大，仅对单方柱进行数值验证是不够全面的^[50]。因此，采用2.1节所述的中等网格对Re = 2×10³串列双方柱进行数值验证。双方柱平均风压系数如图5所示。由于风洞试验来流具有一定的湍流度，导致风压数值存在部分误差。总体来看，上、下游方柱的风压系数分布与风洞试验结果趋势基本一致，但压力数值存在一些误差，这可能是由于风洞试验中无法在方柱角部布置监测点且入口具有一定的湍流强度，而数值模拟中测点布置更为全面且采用了均匀来流，因此导致了结构表面的风压系数存在一定差异。此外，LIU等^[13]研究发现Re = 2×10³串列双方柱在间距比为4时，流动状态为剪切层再附流态，这与本验证算例的模拟结果一致。因此，足以说明本研究采用的数值模拟方法足够准确。

图  5  Re = 2×10³串列双方柱平均风压系数分布

Figure  5.  Distribution of mean wind pressure coefficient on two tandem square cylinders with Re = 2×10³

下载: 全尺寸图片 幻灯片

3   结果与讨论

3.1   流态划分

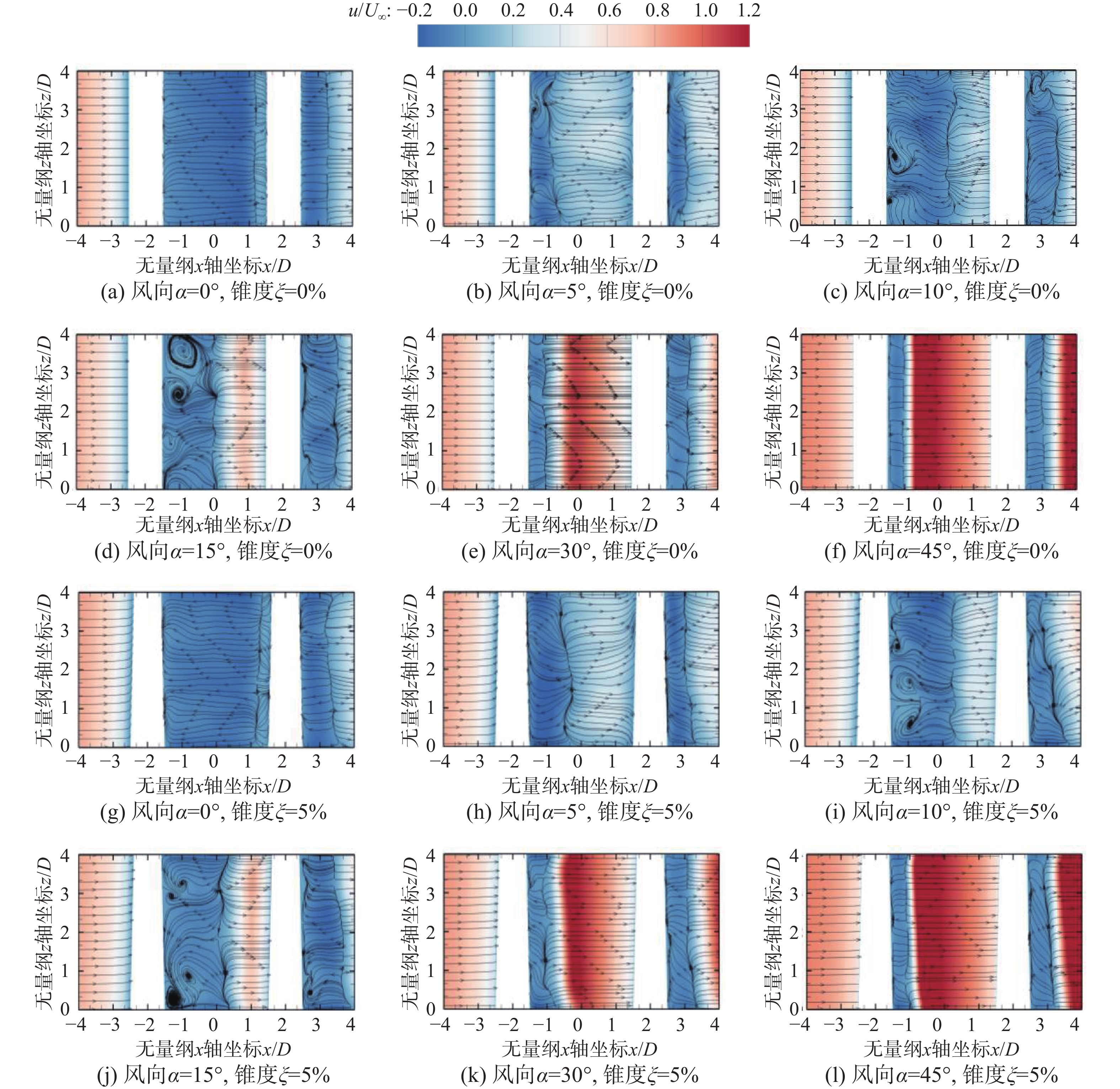
不同风向下z = 0.5H处串列双方柱时均流线如图5所示，采用无量纲平均流向速度$\overline {{u}} /{U_\infty }$进行渲染。参考前人关于单方柱和双方柱绕流的研究^{[18 − 20]}，将串列双方柱流场划分为以下三种流态：前角分离流态(α = 0°)、分离泡流态(α = 5°, 10°, 15°)和附着流流态(α = 30°, 45°)。

当α = 0°时(前角分离流态)，标准串列双方柱仅在下游方柱尾流区产生漩涡脱落。剪切层从上游方柱角点a、b处分离并再附于下游方柱侧面，分别在下游方柱尾流区和迎风面形成对称回流泡和分离泡，柱体间完全被剪切层所占据。

当风向角增大至5°时(分离泡流态)，上游方柱尾流区产生漩涡脱落现象并形成两个回流泡。受上游方柱尾流漩涡的影响，仅下游方柱侧上方形成单个回流泡。剪切层从上游方柱a、b处分离后再附于上游方柱侧面，并在再附位置处形成分离泡。随着风向角的增大，上游方柱侧面形成的分离泡缩小且分离泡核心向角点c和d移动。

当风向角增大至30°和45°时(附着流流态)，上游方柱侧面分离泡逐渐消失。流体在上下游方柱角点b、d处发生分离，并在上、下游方柱尾流区和方柱表面分别形成回流区和分离泡。相较于分离泡流态，附着流流态下的双方柱回流区的长度和宽度明显减小，回流区形状更加对称。如图6(b)所示，采取锥度化措施的双方柱，虽产生了与标准双方柱绕流一致的三种流态，但锥度化措施会导致柱体两侧剪切层宽度逐渐变窄，更靠近柱体表面。同时，z = 0.75H和0.25H处的双方柱平均流线分布也被研究，同样观察到了上述三种流态，并发现随着截面高度的增大，锥度化措施对结构流场尺寸的影响程度逐渐增强，在0.75H处最为显著。上述关于锥度化措施对流场特性的影响与前人研究结论一致^[30]。

图  6  不同风向下双方柱平均流线分布(z = 0.5H)

Figure  6.  Mean streamline distribution of two tandem square cylinders at z = 0.5H profile under different wind directions

下载: 全尺寸图片 幻灯片

3.2   气动力系数

顺风向气动力系数C_Fx和横风向气动力系数C_Fy评估结构抗风性能的两个重要参数，表达式为${{{C_{Fx}} = 2{F_{x}}} / {{\rho _\infty }}}U_\infty ^2DH$和${{{C_{Fy}} = 2{F_{y}}} /{{\rho _\infty }}}U_\infty ^2DH$，其中F_x和F_y分别表示双方柱顺风向和横风向气动力，C_{Fx, A}和C_{Fx, B}分别代表上游方柱和下游方柱。不同风向下串列双方柱局部气动力系数时程如图7和图8所示。当α = 0°时，下游方柱气动力系数的周期性和波动幅度远强于上游方柱，由图6可知，这是由于前角分离流态下的双方柱仅在下游方柱产生漩涡脱落。当双方柱处于分离泡流态时(α = 5°~15°)，上游方柱尾流区产生漩涡脱落，造成上游方柱气动力系数波动程度明显增强。另外，5°风向下的波动较强，这是因为当风向由5°增大至10°和15°时，上游方柱回流泡变长变宽，两侧分离泡逐渐缩减，对表面气动力系数的影响减弱。当风向增大至附着流流态时(α = 30°, 45°)，上、下游方柱尾流区均会产生漩涡脱落，因此气动力系数时程波动程度较为接近。但是，此时下游方柱横风向气动力系数波动程度要弱于上游方柱，这可能是由于该流态下双方柱的漩涡脱落强度有所差异。另外，锥度化措施会显著降低双方柱的气动力脉动特性。这是因为锥度化措施会使结构剪切层宽度变窄，更贴近柱体表面，漩涡能量分布更加分散，进而造成双方柱脉动特性减弱。

图  7  顺风向气动力系数局部时程

Figure  7.  Time history of along-wind aerodynamic coefficient

下载: 全尺寸图片 幻灯片

图  8  横风向气动力系数局部时程

Figure  8.  Time history of cross-wind aerodynamic coefficient

下载: 全尺寸图片 幻灯片

图9展示了双方柱顺风向平均气动力系数${\overline C_{Fx}}$和脉动气动力系数${C_{Fx}^\prime}$随风向的变化情况。顺风向气动力系数总体呈增大趋势，在α = 5°和15°时发生不同程度的突变。根据3.1节流场结构的分析可知，这是因为双方柱在5°和15°下会发生流态转变。如图9(a)所示，前角分离流态下(α = 0°)的下游方柱${\overline C_{Fx}}$呈负值，随着风向角的增大，${\overline C_{Fx}}$逐渐变为正值。此外，上游方柱尾流漩涡会影响下游方柱气动力特性，造成上游方柱平均气动力系数均强于下游方柱。如图9(b)所示，α = 0°时上游方柱${C_{Fx}^\prime}$接近于0，这是因为该流态的上游方柱尾流区未产生漩涡脱落。随着风向角的增大，${C_{Fx}^\prime}$呈现先增大后减小的趋势，在α = 5°时达到最大，且所有风向的下游方柱${C_{Fx}^\prime}$均强于上游方柱。这可能是因为下游方柱受到上游方柱剪切层和尾流漩涡作用，产生了尺度更大的漩涡，进而产生更强的脉动特性。

图  9  不同风向下双方柱顺风向气动力系数变化

Figure  9.  Distribution of aerodynamic coefficients along-wind for two tandem square cylinders under different wind directions

下载: 全尺寸图片 幻灯片

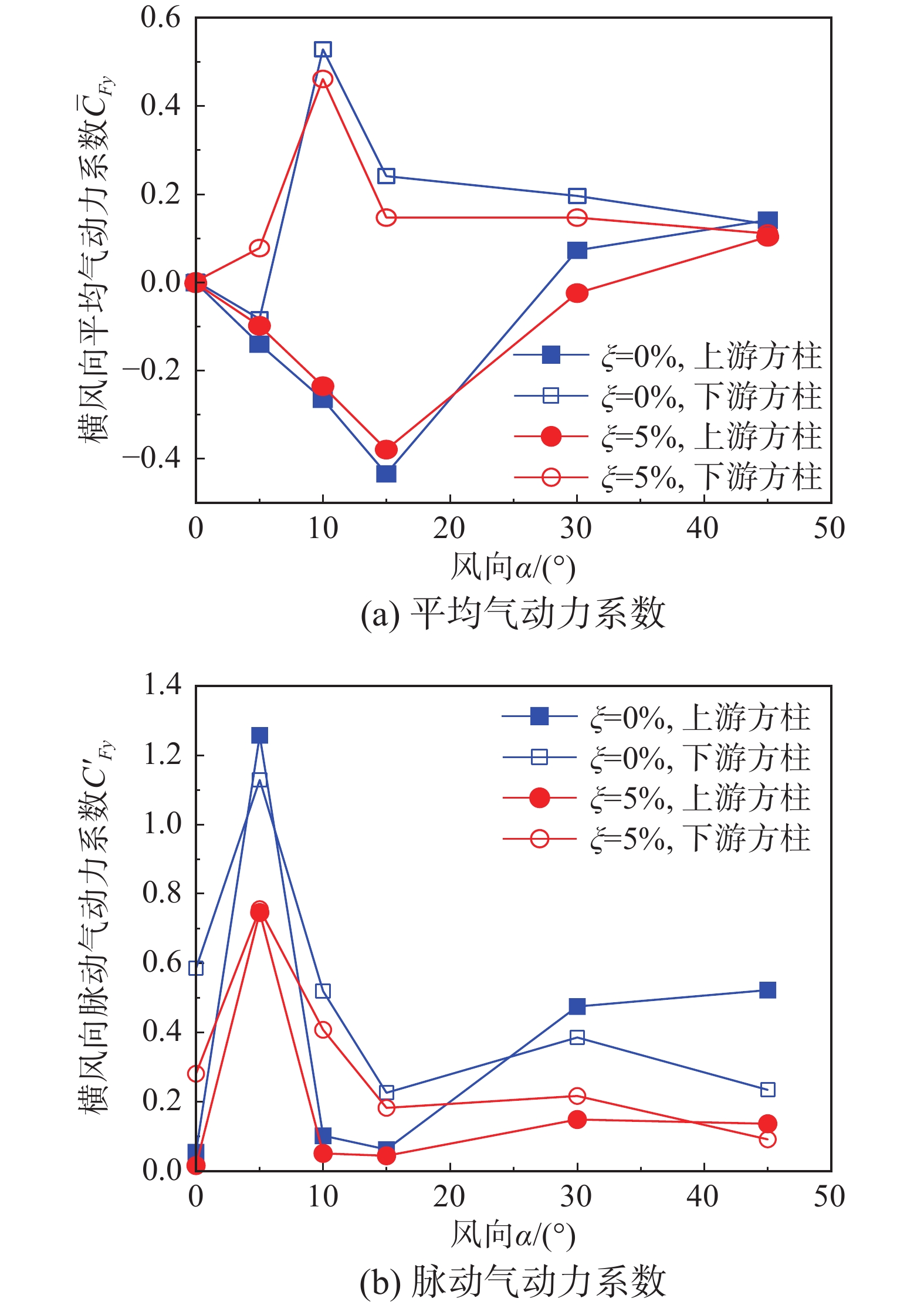
如图10(a)所示，双方柱横风向平均气动力系数${\overline C_{Fy}}$随风向角呈先增大后减小的趋势，α = 0°时${\overline C_{Fy}}$约为0。值得注意的是，上游方柱在分离泡流态时(α = 5°, 10°, 15°)会产生负的${\overline C_{Fy}}$，当风向继续增大并转变为附着流流态时(α = 30°, 45°)，${\overline C_{Fy}}$变为正值。如图10(b)所示，上游方柱横风向脉动气动力系数${C_{Fy}^\prime}$在前角分离流态下(α = 0°)约为0，这是因为该流态下上游方柱未发生漩涡脱落。随着风向角的增大，上游方柱形成漩涡脱落，${C_{Fy}^\prime}$也随之增大。并在分离泡流态时(α = 5°)达到最大，其中标准双方柱${C_{Fy}^\prime}$约为1.2，锥度化措施双方柱${C_{Fy}^\prime}$约为0.7。因此，锥度化措施能够显著降低双方柱的平均和脉动气动力，这与前人的研究结论一致^{[26 − 30]}。

图  10  不同风向下双方柱横风向气动力系数变化

Figure  10.  Distribution of aerodynamic coefficients cross-wind for two tandem square cylinders under different wind directions

下载: 全尺寸图片 幻灯片

不同风向下的幅值谱如图11所示。上、下游方柱幅值谱均存在明显波峰，该波峰所对应的频率被称为漩涡脱落频率f_vs。上下游方柱漩涡脱落频率始终保持一致，且不随风向的增大而变化这与SHANG等^[50]的研究结论一致。随着锥度的增大，双方柱的漩涡脱落频率显著提升，但最大幅值显著降低，即锥度化措施会减弱漩涡脱落产生的能量。另外，当α = 0°, 10°和15°时，下游方柱的最大幅值高于上游方柱，即下游方柱漩涡脱落强度高于上游方柱。而对于其余风向，下游方柱的最大幅值低于上游方柱。同时，双方柱两侧漩涡脱落强度影响横风向气动力系数的脉动特性。由此说明，随着风向的改变，下游方柱横风向脉动气动力系数${C_{Fy}^\prime}$并不总是强于上游方柱，这与图10(b)的变化规律一致。

图  11  不同风向角下双方柱升力幅值谱

Figure  11.  Spectra of lift coefficient amplitudes of two tandem square cylinders under different wind directions

下载: 全尺寸图片 幻灯片

3.3   风压分布

3.3.1   平均风压

选择4种具有代表性的风向α = 0°(前角分离流态)、α = 5°, 10°(分离泡流态)和α = 45°(附着流流态)作进一步研究。z = 0.5H高度处双方柱风压系数随风向的变化如图12所示。对于上游方柱，α = 0°, 5°, 10°时的风压系数分布基本一致，即在迎风面ab处先增大后减小，在驻点位置处(迎风面ab中点附近)风压系数接近于1，经过b点后风压系数基本不变。由于风向的增大，驻点从迎风面ab中点逐渐向a点移动，在α = 45°时移到a点，这是造成45°风向方柱表面风压系数不同于其余三个工况的原因。对于下游方柱，当处于前角分离流态时(α = 0°)，由于上游方柱的遮挡效应，下游方柱表面均受到负压作用(风吸力)，且迎风面的负压绝对值大于背风面，导致下游方柱${\overline C_{Fx}}$呈负值，这与图9(a)的结果一致。下游方柱受两侧分离泡的影响，侧面风压系数均为负值，受到明显的风吸力作用。值得注意的是，对于附着流流态(α = 45°)下的双方柱，风压分布关于后角点c对称，这是因为该风向下双方柱尾流区存在相对对称的回流泡和分离泡。另外，上游方柱侧面和背风面风压系数随锥度的增大而降低，这导致方柱前后表面压差显著降低，这解释了锥度化措施能够降低上游方柱${\overline C_{Fx}}$的原因，如图9(a)所示。同时，也对z = 0.75H(如图13所示)和0.25H处的风压分布进行了探究，发现双方柱表面平均风压系数大小及分布规律基本不随高度的变化而变化。

图  12  不同风向下双方柱平均风压系数分布(z = 0.5H)

Figure  12.  Distribution of mean wind pressure coefficient on two cylinders under different wind directions at z = 0.5H

下载: 全尺寸图片 幻灯片

图  13  不同风向下双方柱平均风压系数分布(z = 0.75H)

Figure  13.  Distribution of mean wind pressure coefficient on two cylinders under different wind directions at z = 0.75H

下载: 全尺寸图片 幻灯片

由3.1节分析和之前研究^[30]可知，双方柱z = 0.5H处的流场差异最为显著，图14展示了双方柱z = 0.5H处平均风压云图分布情况。当α = 0°和5°时，下游方柱表面均呈现负压，且α = 0°时下游方柱迎风面负压强于背风面，而α = 5°时下游方柱迎风面负压弱于背风面，因此下游方柱${\overline C_{Fx}}$在α = 0°和5°时分别呈现负值和正值。当α = 10°和45°时，下游方柱角点a处出现正压区，且正压区范围随风向角的增大而增大。采取锥度化措施的双方柱能够显著缩减结构表面的强压区范围，这解释了下游方柱${\overline C_{Fx}}$随锥度增大而降低的产生原因。另外，从图中可以看出上游方柱迎风面和背风面所受到的风压强度高于下游方柱，产生更大的压差，进而造成上游方柱产生更大的${\overline C_{Fx}}$(见图8(a))。当α = 5°, 10°时(分离泡流态)，由于上游方柱bc和da面产生数值相近的负压区。由此可知，上游方柱出现负的${\overline C_{Fy}}$(见图10)主要是由ab和cd面压差的y方向分量导致的。

图  14  不同风向下双方柱平均风压云图(z = 0.5H)

Figure  14.  Contour map of mean wind pressure on two cylinders under different wind directions at z = 0.5H

下载: 全尺寸图片 幻灯片

3.3.2   脉动风压

如图15展示了不同风向下z = 0.5H处双方柱脉动风压系数分布。当双方柱处于前角分离流态(α = 0°)和分离泡流态(α = 5°, 10°)时，上游方柱脉动风压在四个角点处(a~d)均出现突变。这是由于流体在迎风面角点a和b处发生分离(见图6)，产生的分离剪切层在角点c和d处发生卷起造成的^[13]。随着风向增大至45°, 流体紧贴ab和da面并在角点b和d处分离，造成上游方柱ab和da面脉动风压弱于其余面。此时的上游方柱bc和cd面存在较强的脉动风压，并在角点c处出现最大值。结合图6的分析可知，bc和cd面形成的分离泡增强了表面脉动风压强度，在c点两侧交替的漩涡脱落是c点出现极值脉动风压的原因。由于上游方柱在α = 0°时并未产生漩涡脱落，因此存在最弱的脉动风压。

对于下游方柱，当α = 45°时，脉动风压分布趋势与上游方柱相似，但脉动风压强度明显弱于上游方柱，如图15(b)所示。这是因为上下游方柱在该流态下存在相似的流场结构，且下游方柱漩涡脱落形成区域比上游方柱更长。

图  15  不同风向下双方柱脉动风压系数分布(z = 0.5H)

Figure  15.  Distribution of the fluctuating wind pressure coefficient on two cylinders at z = 0.5H under different wind directions

下载: 全尺寸图片 幻灯片

对于分离泡流态下的双方柱，α = 5°时的下游方柱脉动风压强度远强于α = 10°, 这是因为α = 10°时双方柱间的干扰效果更强，此时上游方柱尾流漩涡会影响下游方柱漩涡脱落的形成和发展，导致下游方柱形成了更长且更宽的回流泡。另外，随着锥度的增大，上下游方柱脉动风压强度明显降低，进一步说明了锥度化措施可以显著降低结构的脉动特性。z = 0.75H处的脉动风压分布情况如图16所示，总体来看，z = 0.75H脉动风压分布规律与z = 0.5H基本一致。同样，z = 0.25H处的脉动风压分布规律也基本与z = 0.5H一致，受篇幅限制不再展示。

图  16  不同风向下双方柱脉动风压系数分布(z = 0.75H)

Figure  16.  Distribution of the fluctuating wind pressure coefficient on two cylinders at z = 0.75H under different wind directions

下载: 全尺寸图片 幻灯片

3.4   流场特性

图17进一步展示了z = 0.75H截面瞬时涡量。选取下游方柱两个典型时刻进行分析，t₁和t₂分别为升力系数最大和最小值对应时刻，蓝色和红色分别表示顺时针和逆时针方向的展向涡量。双方柱瞬时涡量分布存在三种明显不同的流动状态。当α = 0°时，漩涡由上游方柱a，b角点处分离，形成的剪切层再附于下游方柱侧面，柱体间未形成漩涡脱落。当风向角增大至5°和10°, 形成的剪切层直接作用于上游方柱侧面(ad和bc面)并在柱体间形成漩涡脱落。同时，上游方柱尾流漩涡会作用于下游方柱，并与下游方柱尾流共同形成漩涡脱落。当风向达到45°时，漩涡由上游方柱b、d角点处分离，形成的剪切层在bc和cd面形成再附并在柱体间形成漩涡脱落。这三种流态特征与3.1节的现象一致，即前角分离(α = 0°)、分离泡(α = 5°, 10°)和附着流流态(α = 45°)。

图  17  不同风向下双方柱瞬时涡量w_zD/U_∞变化(z = 0.75H)

Figure  17.  Instantaneous vorticity w_zD/U_∞ of two tandem cylinders under different wind directions

下载: 全尺寸图片 幻灯片

在前角分离和分离泡流态下，上游方柱产生的尾流漩涡会作用于下游方柱表面。随着风向角增大，柱体间的干扰效应在附着流流态逐渐减弱，双方柱呈现出独立的漩涡脱落状态。柱体间表现出偏向流的特点。由于间歇流的偏转，导致下游方柱的漩涡脱落形成区域更宽更长，因此下游方柱具有更弱的脉动特性及漩涡脱落能量，这与图10(b)和图11的结果一致。此外，与标准双方柱相比，锥度化措施会使剪切层宽度逐渐变窄，更加贴近柱体表面，导致柱体间生成更加破碎、尺度更小的漩涡，减弱了漩涡脱落的脉动特性。

进一步对x – z截面(y = 0)时间平均流线进行分析，如图18所示。从图中可以看出，由于入口采用均匀来流，导致上游方柱迎风面流线均匀分布，但在其背风面产生了向上发展的旋涡，这说明在Re=2×10³时，串列双方柱绕流存在三维流动特性。对于采用锥度化措施的串列双方柱，流场中产生了更加明显的三维效应和三维涡结构。在前角分离流态下(α = 0°)，标准和锥度化双方柱体间均出现了回流现象，但未观察到明显的漩涡脱落现象，这是由于α = 0°时，在柱体间形成的两个漩涡是对称的，如图6所示。而在分离泡流态下(α = 5°, 10°, 15°)，结合图6中的时间平均流线，此时双方柱间的漩涡不对称且柱间干扰效应较强，因此可以观察到明显的漩涡脱落现象。在附着流流态下(α = 30°, 45°)，由于双方柱间的干扰效应减弱，相比于分离泡状态，回流长度显著减小。

图  18  不同风向下双方柱y = 0切面时间平均流线

Figure  18.  Mean streamline distribution of two tandem cylinders under different wind directions at y = 0 profile

下载: 全尺寸图片 幻灯片

串列双方柱涡量等值面如图19所示，采用Q准则进行计算(Q = 0.1U_∞²/D²)，并采用无量纲瞬时流向速度u/U_∞进行渲染^{[51 − 52]}。在前角分离流态下(α = 0°)，剪切层从上游方柱分离后再附于下游方柱侧面，在下游方柱尾流区细长肋状涡会伴随着漩涡脱落而产生。随着风向角的增大，在分离泡(α = 5°, 10°)和附着流流态下(α = 45°)，双方柱尾流区细长肋状涡逐渐消失，流场三维流动特性增强且展向相关性减弱，在α = 5°时最为显著。另外，在α = 5°时，双方柱两侧剪切层和尾流漩涡脱落形成区域更短，漩涡对结构的作用显著增强。这导致5°风向下的双方柱具有更强的脉动特性，产生更小的漩涡脱落频率和更强的漩涡脱落能量，如图10(b)和图11所示。

图  19  不同风向下双方柱三维涡量等值面(Q = 0.1U_∞²/D²)

Figure  19.  Instantaneous equivalent surface at Q = 0.1U_∞²/D² under different wind directions

下载: 全尺寸图片 幻灯片

3.5   气动力拟合

为更好地将研究成果应用于大跨桥梁H形桥塔等串列结构的设计和建造中，采用最小二乘法拟合出风向角与气动力系数间的数学关系式。同时对风向为20°、25°、35°和40°的串列双方柱进行数值模拟，提高拟合公式的可靠性和准确性。拟合曲线如图20所示，总体来看，风向角与双方柱顺风向平均力系数${\overline C_{Fx}}$和横风向脉动力系数${C_{Fy}^\prime}$间的拟合效果较好，呈非线性变化规律。与标准双方柱相比，采用锥度化措施双方柱的拟合曲线均位于其下方，说明锥度化措施能够显著降低结构气动力系数。具体的数学关系公式如式(7)~式(14)所示，拟合后的确定性系数R²值依次为：0.901、0.845、0.976、0.981、0.797、0.814、0.615和0.700。可以看出，平均力系数的拟合效果较好，均在0.8以上。脉动力系数的拟合结果在某些位置会有一些突变(图20(c)中20°和图20(d)中10°和15°)产生这种现象的原因是，脉动气动力特性与双方柱的漩涡脱落联系十分密切，从流态划分(图6)来看，双方柱的漩涡脱落十分复杂，因此导致了脉动特性变化较大，在某些风向下出现了显著变化。

图  20  串列双方柱气动力系数与风向角拟合曲线

Figure  20.  Fitted curve of aerodynamic coefficient and wind direction angle for two tandem square cylinders

下载: 全尺寸图片 幻灯片

ξ = 0%，0°≤α≤45°，上游方柱:

ξ = 5%，0°≤α≤45°，上游方柱:

ξ = 0%，0°≤α≤45°，下游方柱:

ξ = 5%，0°≤α≤45°，下游方柱:

ξ = 0%，0°≤α≤45°，上游方柱:

ξ = 5%，0°≤α≤45°，上游方柱:

ξ = 0%，0°≤α≤45°，下游方柱:

ξ = 5%，0°≤α≤45°，下游方柱：

4   结论

本文采用大涡数值模拟方法对雷诺数Re = 2×10³、间距比G/D = 4、锥度ξ = 0%，5%条件下的串列双方柱进行研究，探究了不同风向(α = 0°~45°)对双方柱流场形态、气动力和风压分布的影响，从瞬时涡结构角度揭示了气动特性的变化机理，最后建立了风向角与气动力系数间的数学公式。主要研究结论如下：

(1)采用锥度化措施的双方柱会产生与标准双方柱绕流一致的三种流态。锥度化措施会导致柱体两侧剪切层宽度逐渐变窄，更靠近柱体表面，同时也会造成柱体回流区更加细长。根据风向角可将不同锥度下(ξ = 0%、5%)中等间距比(G/D = 4)双方柱绕流划分为前角分离(α = 0°)、分离泡(α = 5°, 10°, 15°)和附着流(α = 30°, 45°)三种流动状态。

(2)锥度化措施会显著影响串列双方柱的气动力特性和风压分布。随着锥度的增大，双方柱气动力系数、表面风压强度和漩涡脱落能量显著降低，但漩涡脱落频率显著提升。当风向角不同时，标准和锥度化双方柱平均、脉动力系数和漩涡脱落频率在流态转变位置处(α = 5°, 15°)发生突变，在α = 5°处的突变程度更强，且存在最大的脉动特性和漩涡脱落强度，但具有最小的漩涡脱落频率。受迎风面强负压作用的影响，下游方柱顺风向平均气动力系数在前角分离流态时(α = 0°)为负值；受迎风面和背风面压差的y方向分量影响，上游方柱横风向平均气动力系数在分离泡流态时(α = 5°, 10°, 15°)为负值。

(3)风向角和锥度化措施显著影响双方柱剪切层和漩涡脱落的形成和发展。锥度化措施会导致剪切层更贴近柱体表面，减弱漩涡脱落的一致性和脉动特性，进而造成双方柱气动力系数和漩涡脱落能量降低。当风向角不同时，前角分离(α = 0°)和分离泡流态下(α = 5°, 10°, 15°)剪切层和尾流漩涡分别再附和撞击下游方柱表面；随着风向角增大至附着流流态(α = 30°, 45°)，上述现象消失但柱体间表现出偏向流特点。风向角α = 5°时，双方柱存在更短的漩涡脱落形成区域和更强的三维特性，导致结构产生更强的脉动特性。