采用数值方法求解结构-地基动力相互作用或近场波动问题时，需要在有限计算模型的截断位置施加人工边界条件，以考虑半无限地基的辐射阻尼效应^[1]。按照时空特性，无限域数值模拟方法可分为全局类方法、局部类方法^[2]：前者时空耦合，理论基础较为严格，具有较高的计算精度，但囿于计算量大、效率低；后者具备时空解耦、计算高效、适用性强等特点，并且计算精度可满足工程需求，因此应用广泛。

局部类人工边界条件主要包括无限元法^[3]、透射边界^[4]、粘性边界^[5]及粘弹性边界^{[6 − 7]}等。其中，粘弹性边界由并联的弹簧和阻尼器元件构成，它克服了粘性边界低频漂移的缺点，物理意义明确，模拟精度与计算效率均较高，在实际中应用广泛^{[8 − 9]}。但在实际工程应用时，需进行一定的前处理工作，来生成计算模型截断边界节点的弹簧—阻尼器系统。为使其更易于实现，刘晶波和谷音等^{[10 − 11]}在集中粘弹性边界的基础上，推导了一致粘弹性边界，并基于此提出一种粘弹性边界单元，通过粘弹性边界单元的刚度矩阵等效一致弹簧元件、与刚度矩阵成正比的阻尼矩阵等效一致阻尼器元件，即阻尼器元件连续均匀分布在地基截断边界表面，实现了采用常规有限元单元模拟粘弹性边界，在实际工程动力分析中应用广泛^{[12 − 15]}。

而在显式动力计算时，由于与刚度成正比的阻尼为非对角矩阵，此时中心差分法仍为隐式格式，丧失了显式格式高效计算的优越性。虽然可采用中心差分结合单边差分法克服这一缺陷，但此时仅为一阶计算精度。另一方面，系统最大稳定步长也会限制显式算法的计算效率。而由于粘弹性边界单元质量、刚度和阻尼参数的影响，人工边界区的稳定性比内部介质的稳定性条件更为严格^{[16 − 18]}，降低了整体系统显式动力计算效率。鉴于此，刘晶波和李述涛等^{[18 − 20]}提出，在不超过内部介质密度的前提下增加粘弹性边界单元的质量密度，可在保证计算精度的同时，有效改善系统显式动力计算的数值稳定性。

本文在文献^{[10 − 11]}的基础上，用与集中质量矩阵成正比的阻尼矩阵等效集中阻尼器元件，即阻尼器元件集中分布在地基截断边界的节点上，推导了一种基于质量比例阻尼的粘弹性边界单元，可保证阻尼矩阵的对角特性，有利于保持传统中心差分法的计算效率，并且阻尼矩阵不受边界单元厚度的影响。与基于刚度比例阻尼的粘弹性边界单元对比，分析了两种粘弹性边界单元表达形式下显式计算的数值稳定性。最后，以半无限空间点源激励问题、某重力坝纯动力反应分析为例，验证了阻尼矩阵与集中质量矩阵成正比的粘弹性边界单元的计算精度。

1   二维粘弹性边界单元等效物理参数

1.1   文献^{[10 − 11]}中阻尼与刚度成正比的表示方式

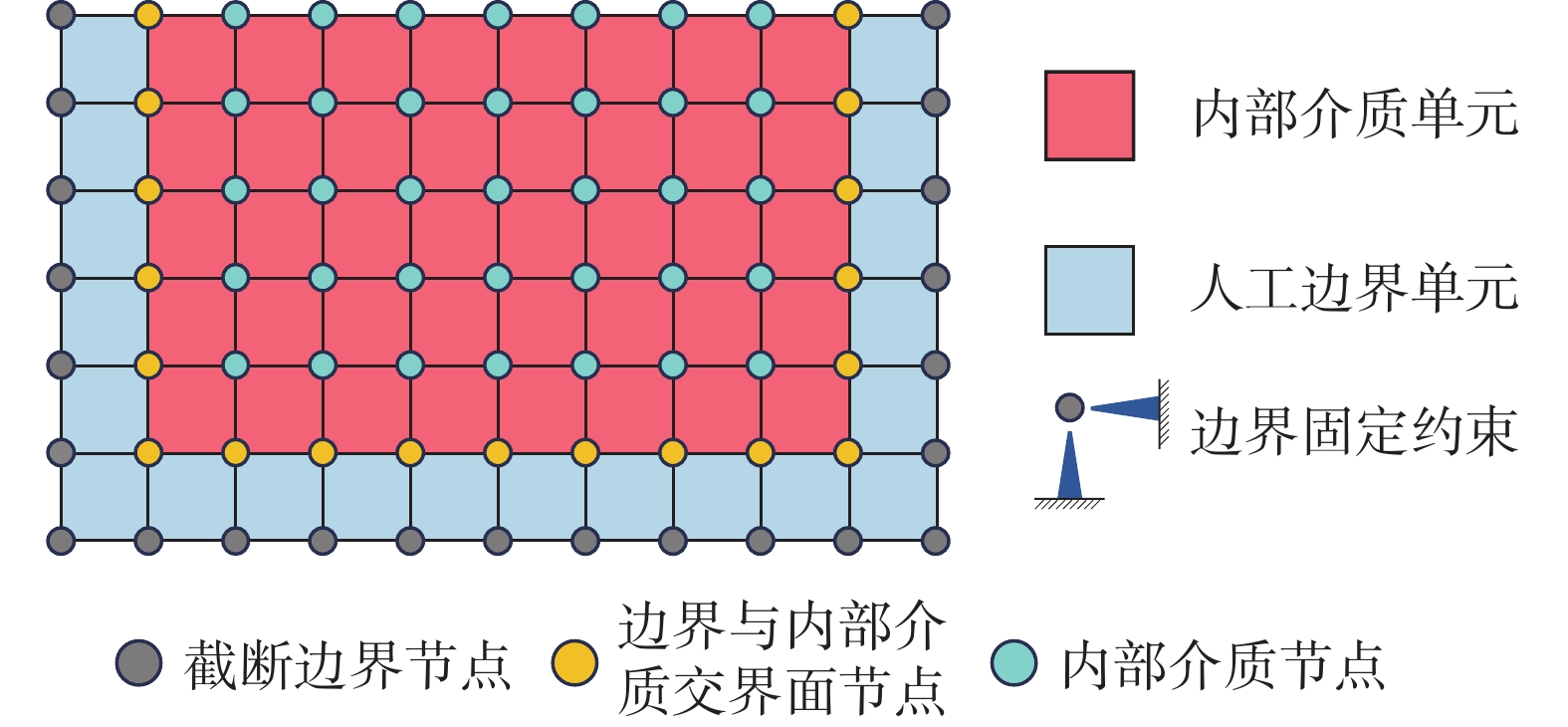
如图1所示，对于二维问题，沿截断地基边界的法线方向向外延伸一层单元，对最外侧节点施加固定约束，便得到粘弹性人工边界单元。粘弹性边界单元的等效弹性模量$\tilde E$、等效泊松比$\tilde \nu$和等效阻尼比例系数$\tilde \eta$分别为：

式中：${\alpha _{\rm N}}$、${\alpha _{\rm T}}$分别为法向和切向粘弹性人工边界参数，二维问题推荐值为1和0.5^[21]；$h$为粘弹性边界单元厚度，理论上应远小于内部单元尺寸，但敏感性分析表明$h$可灵活取值而对计算结果影响很小，一般可取内部单元尺寸^[10]；$G$为内部介质剪切模量；$R$为散射波源到边界节点的距离；$\rho$为内部介质密度；${c_{\rm p}}$和${c_{\rm s}}$分别为内部介质P波与S波波速；${{\boldsymbol{K}}_{\rm B}}$、${{\boldsymbol{C}}_{\rm B}}$分别为粘弹性边界单元刚度与阻尼矩阵。

图  1  粘弹性边界单元示意图

Figure  1.  Diagram of 2D viscous-spring boundary element

下载: 全尺寸图片 幻灯片

粘弹性边界单元的密度$\tilde \rho$，在隐式动力计算时，可设置为0；在显式动力分析时，可适当增大以改善数值稳定性，本文中设置为内部介质密度$\rho$。

1.2   本文提出的阻尼与集中质量成正比的表示方式

本文中，粘弹性人工边界单元的等效弹性模量、等效泊松比直接采用式(1)和式(2)进行计算，以保证粘弹性边界单元的刚度矩阵可等效一致粘弹性人工边界的弹簧元件。粘弹性边界单元的密度设置为$\tilde \rho$，考虑图1中最外侧节点的固定约束条件，可得二维粘弹性边界单元集中质量矩阵为：

式中，${\boldsymbol{I}}$为4×4单位矩阵。

粘弹性边界单元的阻尼矩阵采用与集中质量矩阵成比例的形式，即：

其中：

使用粘弹性边界单元的阻尼矩阵来等效集中粘弹性人工边界的阻尼器元件，即：

联立式(5)~式(8)可以得到：

为实施方便，采用各向同性的材料阻尼系数，将粘弹性边界单元的阻尼比例系数$\tilde \alpha$设置为两个方向的平均值：

若进一步将粘弹性边界单元密度设置为内部介质密度，可得：

至此，便推导出基于与质量成比例的阻尼的粘弹性边界单元，根据式(1)和式(2)计算粘弹性单元的弹性模量与泊松比，采用质量比例阻尼的假设，等效的比例阻尼系数$\tilde \alpha$可根据式(11)进行计算。

综上可以看出，对于传统基于刚度比例阻尼的等效粘弹性边界单元，阻尼矩阵为非对角阵，此时中心差分法为隐式格式，丧失了高效计算效率。而本文提出的基于质量比例阻尼的等效粘弹性边界单元，阻尼矩阵为对角矩阵，可保证传统中心差分法的显式计算格式，进而保证计算效率。此外，使用与刚度成正比的阻尼推导的粘弹性边界单元，其阻尼矩阵代表的是一致粘弹性边界，并且在推导过程中引入了粘弹性边界单元厚度远小于内部单元尺寸这一假定；而使用与集中质量成正比的阻尼表示的粘弹性边界单元，其阻尼矩阵代表的是集中阻尼器元件，阻尼矩阵不受单元厚度的影响。

2   显式算法的数值稳定性分析

2.1   基于局部子系统的数值稳定性分析方法

显式算法的计算效率受到系统最大稳定步长的限制，显式算法稳定性分析的目的是获得满足数值稳定性要求的时间离散步长$\Delta t$的限制条件。对于实际计算模型，囿于复杂的边界条件与大规模自由度，难以通过冯诺伊曼方法或系统整体传递矩阵谱半径分析方法，给出解析形式的稳定性条件。李述涛等^[19]对一维剪切梁与二维平面问题的稳定性进行分析，提出一种利用代表性局部子系统估算整体计算模型数值稳定性的方法。根据该方法，对于实际计算模型，首先进行模型分析，选取能反映整体模型不同局部特征的代表子系统，子系统的特点是只包含一个运动节点。通过分析所有代表子系统的稳定步长要求，选取其中最严格的稳定性条件作为整体模型的显式算法时间离散步长$\Delta t$的上限估计。

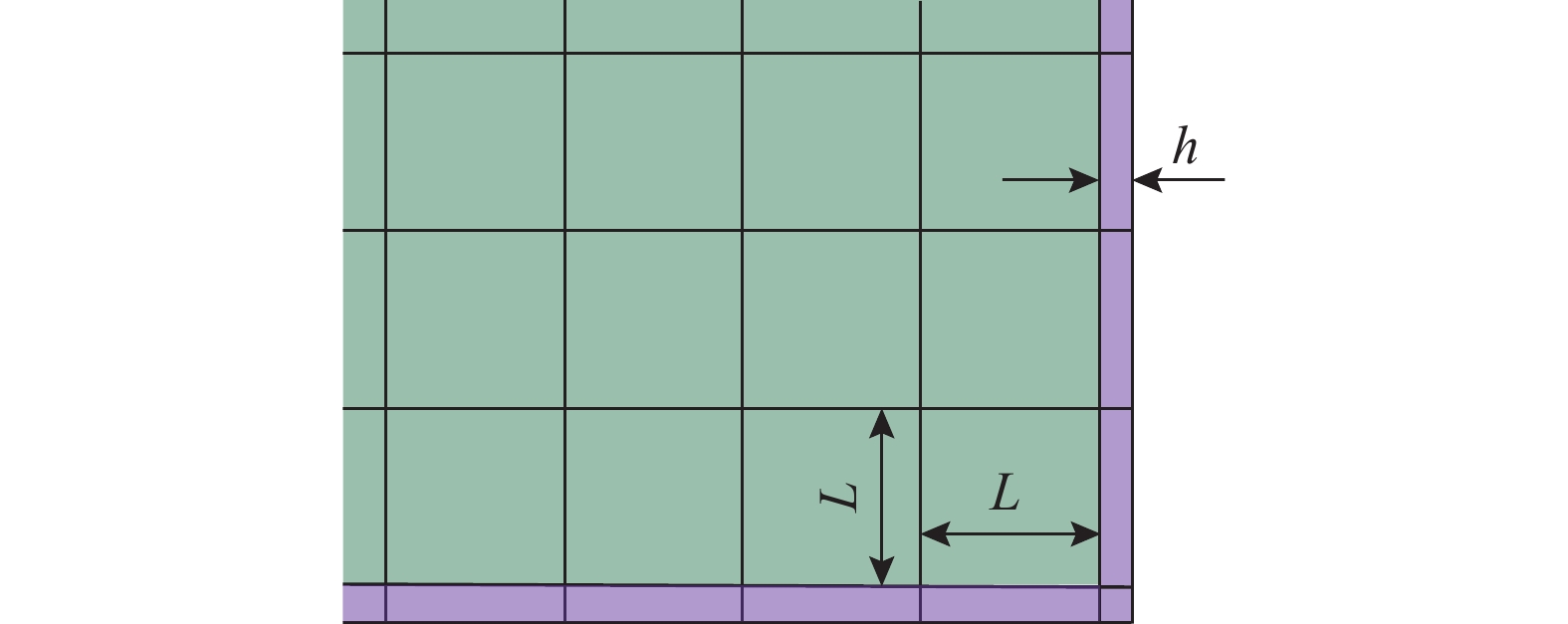
具体来说，针对粘弹性边界单元，如图2所示，本文假设内部为均匀介质，采用规则均匀网格进行离散；取粘弹性边界单元密度$\tilde \rho = \rho$、厚度$h = L$。内部介质的稳定性条件容易获得，即：

图  2  考虑粘弹性人工边界单元的整体计算模型

Figure  2.  Overall computational model with viscous-spring boundary elements

下载: 全尺寸图片 幻灯片

在边界处，如图3所示，可以分离出两个代表性子系统：侧边子系统与角点子系统。代表子系统的特点为：由四个单元组成，子系统的边界节点为固定约束条件，只包含内部一个运动节点。随后，根据显式逐步积分算法格式与运动方程形式，分别写出每个代表子系统的如下递推关系：

式中：${\boldsymbol{A}}$为传递矩阵；${\boldsymbol{Q}}$为荷载向量；${\boldsymbol{U}}$为由子系统运动节点的速度、位移和加速度组成的向量，对于二维问题，若采用蛙跳格式的中心差分法，具体形式为：

图  3  两种边界代表子系统(图例同图2)

Figure  3.  Two representative subsystems of the viscous-spring boundary elements (refer to legend in Figure 2)

下载: 全尺寸图片 幻灯片

由稳定性分析原理可知，任一积分格式的稳定性条件仅依赖于其传递矩阵${\boldsymbol{A}}$的特征值，记${\lambda _i}$为传递矩阵${\boldsymbol{A}}$的第$i$个特征值，传递矩阵${\boldsymbol{A}}$的谱半径为$\rho \left( {\boldsymbol{A}} \right) = \max \left| {{\lambda _i}} \right|$，则代表子系统数值积分稳定性的条件为：

文献^[16]对基于与刚度成比例的阻尼的粘弹性边界单元显式计算稳定性进行了推导。本文为方便进行对比，按照文献^[16]中的方法，稳定性分析时采用蛙跳格式的中心差分法。其特点是，在半个时间步上得到速度。递推公式为：

对应的系统基本运动方程为：

式中：${\boldsymbol{M}}$、${\boldsymbol{K}}$和${\boldsymbol{C}}$分别为系统的质量、刚度与阻尼矩阵；${\boldsymbol{F}}$为荷载向量。

2.2   侧边子系统稳定性对比

侧边子系统如图3(a)所示，由两个内部介质单元和两个粘弹性边界单元构成，子系统四周为固定约束，仅中间节点1为自由节点。如前文所述，这里假设粘弹性边界单元密度$\tilde \rho = \rho$，粘弹性边界单元厚度$h = L$。

当采用基于与刚度成正比的阻尼的粘弹性边界单元时，可直接采用李述涛等^[16]推导得到的侧边子系统的稳定性条件，即：

其中：

式中，稳定性系数${\gamma _{{\rm e}1}}$为一无量纲系数，只和内部介质泊松比$\mu$与${R \mathord{\left/ {\vphantom {R L}} \right. } L}$相关。

当采用基于与质量成正比的阻尼的粘弹性边界单元时，对于图3(a)所示侧边子系统，将各单元集中质量矩阵、阻尼矩阵与刚度矩阵进行组装，可得侧边子系统的自由节点1的运动方程为：

其中：

观察式(21)可以看出，侧边子系统在x和y两个方向的运动方程是解耦的，并且形式一致，因此可以只对其中任一方向的运动方程进行稳定性分析。

根据式(17)和式(18)，将式(21)任一方向进行展开，可得传递矩阵形式：

式中，传递矩阵${{\boldsymbol{A}}_{{\rm e}2}}$为：

根据稳定性判别条件$\rho \left( {{{\boldsymbol{A}}_{{\rm e}2}}} \right) {\leqslant} 1$可得：

式中，稳定性系数${\gamma _{{\rm e}2}}$为一无量纲系数，只和内部介质泊松比$\mu$与${R \mathord{\left/ {\vphantom {R L}} \right. } L}$相关。

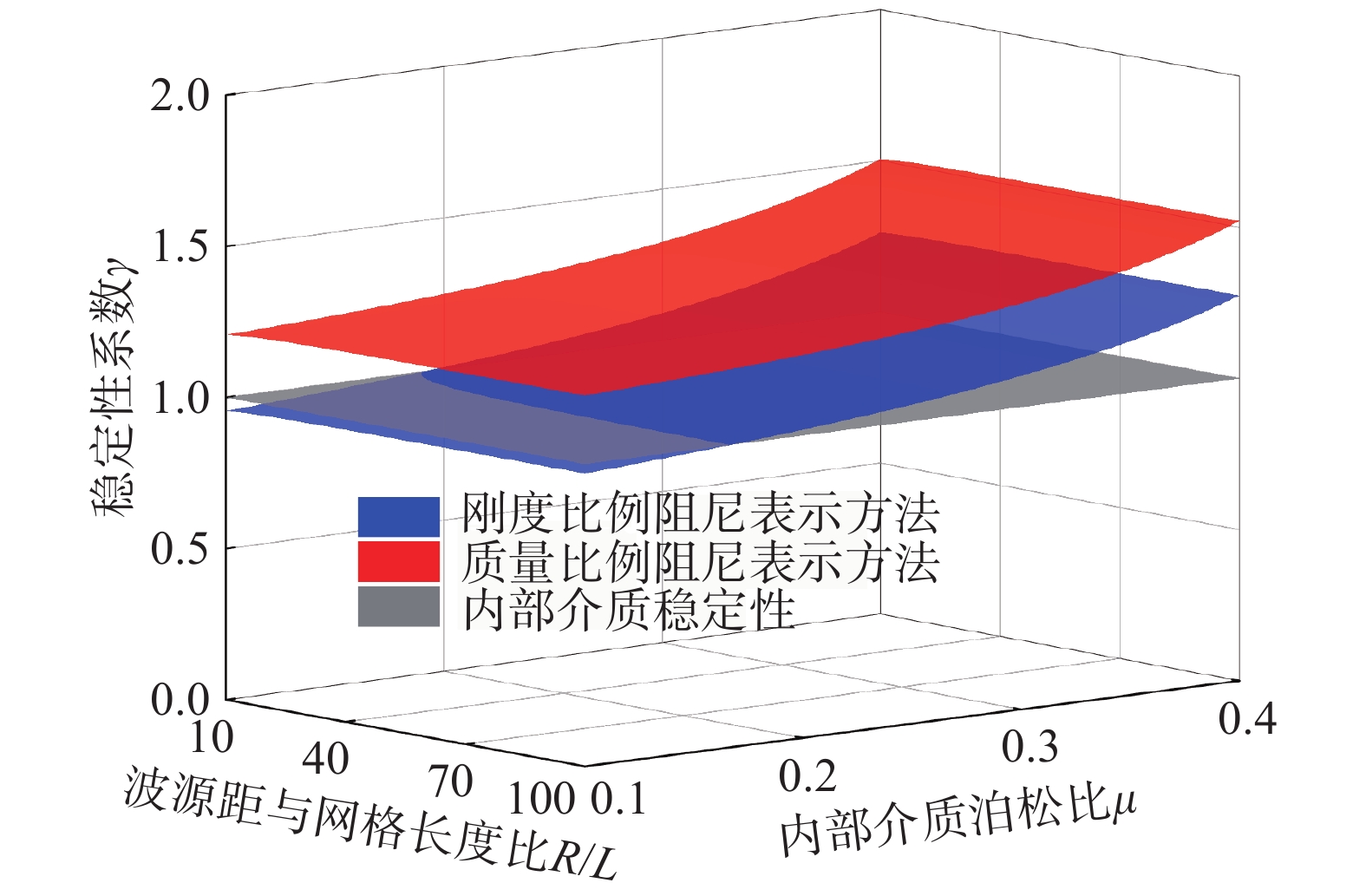
式(19)和式(25)分别给出了采用刚度比例阻尼和质量比例阻尼表示粘弹性边界单元时，侧边子系统的稳定性条件，可以看出，二者在方程形式上一致，只是参数存在差异。图4展示了两种表示方式下，侧边子系统的稳定性系数随$\mu$与${R \mathord{\left/ {\vphantom {R L}} \right. } L}$变化情况，考虑参数应具有实际工程意义，${R \mathord{\left/ {\vphantom {R L}} \right. } L}$的变化范围限制在10~100，内部介质泊松比的变化范围为限制在0.1~0.4。

图  4  两种表示方式下侧边子系统稳定性条件比较

Figure  4.  Comparison of stable conditions of edge subsystem coefficient under two representations

下载: 全尺寸图片 幻灯片

可以看出：①当粘弹性边界单元密度取为内部介质密度时，采用两种阻尼表示方式的粘弹性边界单元，其侧边子系统的稳定性系数均大于1，表示侧边子系统的数值稳定性条件比内部介质的更为宽松；②对于侧边子系统，在工程关注的参数范围内，使用与集中质量成正比的阻尼表示时，边界子系统的稳定性要优于使用与刚度成正比的阻尼的表示方式。

2.3   角点子系统稳定性对比

角点子系统如图3(b)所示，由1个内部介质单元和3个粘弹性边界单元构成，子系统四周为固定约束，仅中间节点1为自由节点。如前文所述，这里假设粘弹性边界单元密度$\tilde \rho = \rho$，粘弹性边界单元厚度$h = L$。

当采用刚度比例阻尼矩阵表示的粘弹性边界单元时，可直接采用李述涛等^[16]推导得到的角点子系统的稳定性条件，即：

其中：

式中，稳定性系数${\gamma _{{\rm c}1}}$为一无量纲系数，只和内部介质泊松比$\mu$与${R \mathord{\left/ {\vphantom {R L}} \right. } L}$相关。

当使用与质量成正比的阻尼矩阵表示粘弹性边界单元时，对于图3(b)所示角点子系统，将各单元集中质量矩阵、阻尼矩阵与刚度矩阵进行组装，可得角点子系统的自由节点1的运动方程为：

其中：

根据式(17)和式(18)，将式(28)进行展开，可得传递矩阵形式：

式中，传递矩阵${{\boldsymbol{A}}_{{\rm c}2}}$为：

根据稳定性判别条件$\rho \left( {{{\boldsymbol{A}}_{{\rm c}2}}} \right) {\leqslant} 1$可得：

式中，稳定性系数${\gamma _{{\rm c}2}}$为一无量纲系数，只和内部介质泊松比$\mu$与${R \mathord{\left/ {\vphantom {R L}} \right. } L}$相关。

式(26)和式(32)分别给出了采用刚度比例阻尼和质量比例阻尼表示粘弹性边界单元时，角点子系统的稳定性条件。图5展示了两种表示方式下，角点子系统的稳定性系数随$\mu$与${R \mathord{\left/ {\vphantom {R L}} \right. } L}$变化情况，考虑参数应具有实际工程意义，${R \mathord{\left/ {\vphantom {R L}} \right. } L}$的变化范围限制在10~100，内部介质泊松比$\mu$的变化范围为限制在0.1~0.4。

图  5  两种表示方式下角点子系统稳定性条件比较

Figure  5.  Comparison of stable conditions of corner subsystem coefficient under two representations

下载: 全尺寸图片 幻灯片

从图5可以看出：①当粘弹性边界单元密度取为内部介质密度时，使用与刚度成正比的阻尼表示时，当泊松比$\mu$在0.1~0.2，稳定性系数${\gamma _{{\rm c}1}}$存在小于1的情况，即角点子系统的稳定性条件比内部介质更为严格，成为系统数值稳定性的控制因素，这与文献^[19]中的结果一致；②使用与集中质量成正比的阻尼表示粘弹性边界单元时，角点子系统稳定性系数全部大于1，表明此时角点子系统的数值稳定性比内部介质更为宽松；③对于角点子系统，在工程关注的参数范围内，使用与质量成正比的阻尼表示方式时，角点子系统的稳定性要优于使用与刚度成正比的阻尼的表示方式。

3   计算精度分析

3.1   半无限空间点源激励问题

选取均质半无限空间点源激励问题作为分析案例。有限元网格如图6所示，模型大小为200 m×100 m，内部介质密度为2600 kg/m³，弹性模量为10 GPa，泊松比取为0.167，网格尺寸为2 m，在模型点A处施加持时为0.2 s的脉冲荷载，时程曲线如图7所示。

分别考虑4种边界情况：① 远置边界，作为该问题的数值精确解；② 传统方法中基于刚度比例阻尼的粘弹性边界单元；③ 本文所提出的基于质量比例阻尼的粘弹性边界单元；④ 基于瑞利阻尼的粘弹性边界单元，其刚度比例阻尼系数与质量比例阻尼系数分别取式(3)与式(11)的1/2。不同边界条件下，B、C两点的加速度时程曲线如图8所示，可以看出，两种粘弹性边界结果基本一致，与远置边界的计算结果非常接近，表明两种方法具有相似的计算精度。当边界单元采用瑞利阻尼时，计算结果位于基于刚度比例阻尼与基于质量比例阻尼的算例之间。

图  6  均匀半无限空间模型

Figure  6.  The uniform half space model

下载: 全尺寸图片 幻灯片

图  7  荷载示意图

Figure  7.  The load function

下载: 全尺寸图片 幻灯片

图  8  不同观测点加速度时程对比

Figure  8.  The acceleration of observe points

下载: 全尺寸图片 幻灯片

进一步地，对比两种等效粘弹性边界单元的显式算法数值稳定性。根据材料参数与网格尺寸，通过前文中理论分析与试算，可知对于采用传统基于刚度比例阻尼的粘弹性边界单元的工况，当显式计算时间步长取0.000 94 s时，模型角点系统会在计算时发生失稳，如图9所示。而当采用本文提出的基于质量比例阻尼的粘弹性边界单元时，当显式计算时间步长取0.000 94 s时，系统能稳定完成动力计算。表明本文所提出的等效粘弹性边界单元在显式计算中的数值稳定性优于传统方法。

图  9  采用基于刚度比例阻尼的边界单元时系统失稳状态

Figure  9.  The unstable state of the system when using the stiffness-proportional damping

下载: 全尺寸图片 幻灯片

3.2   重力坝-地基系统地震反应分析

进一步选取某重力坝作为研究对象，分析所提出的粘弹性边界单元表示方式的计算精度。

该重力坝高100 m，坝体—地基系统有限元网格如图10所示，为保证计算精度与计算效率，地基向上、下游与深度方向各延伸2倍坝高^[22]。坝体采用四节点平面应力单元进行模拟(CPS4)，地基采用四节点平面应变单元(CPE4)。坝体包含1069个网格，网格尺寸为2 m；地基包含5528个网格，网格尺寸由坝基处的2 m向地基深部与上下游方向进行过渡，最大网格尺寸约15 m。上游库水深度为85 m，采用Westergaard附加质量方法模拟动水压力作用。

图  10  坝体—地基系统有限元模型

Figure  10.  Finite element model of the gravity dam-foundation rock system

下载: 全尺寸图片 幻灯片

坝体混凝土密度取为2400 kg/m³，动弹性模量取为36 GPa，泊松比取为0.17；基岩密度为2600 kg/m³，弹性模量取为15 GPa，泊松比取为0.25。坝体的材料阻尼假定为Rayleigh阻尼，阻尼比设置为5%，采用第一、第五阶自振频率计算Rayleigh阻尼比例系数，按照文献^[22]中的研究结论，忽略地基材料阻尼。

为直观比较两种粘弹性边界单元的效果，计算荷载条件设置为纯动力。假设地震动垂直入射，采取一维波动理论求解地基自由场运动，根据域缩减法^{[23 − 24]}，将自由场运动转化为等效地震荷载。图11为用于计算等效地震荷载的地表自由场加速度时程，水平向地震动峰值加速度为4 m/s²，竖向地震动峰值加速度取为水平向的2/3。

图  11  输入地震动地表自由场加速度时程

Figure  11.  The free field acceleration of input ground motion

下载: 全尺寸图片 幻灯片

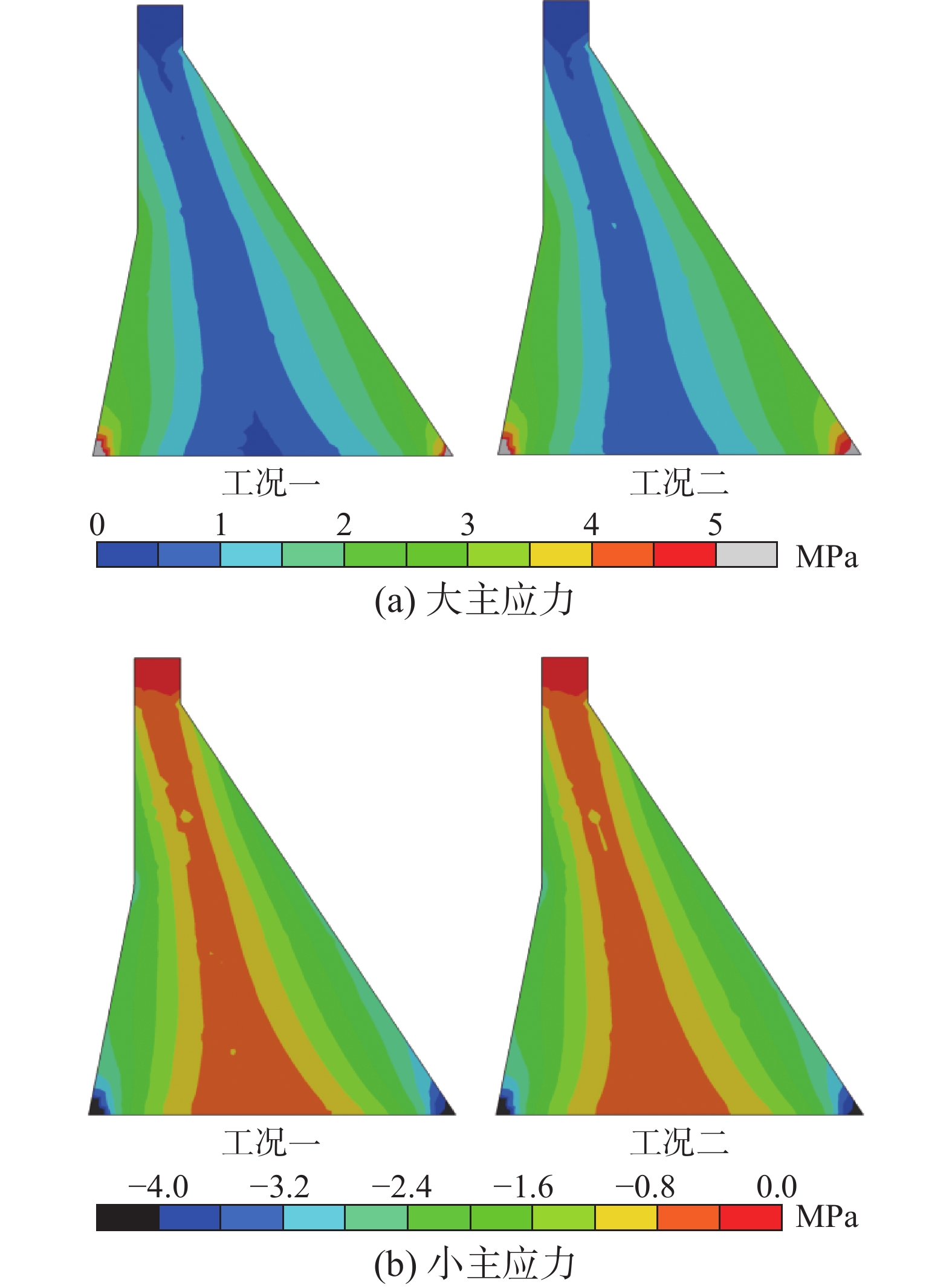
图10中的粘弹性边界单元参数分别采用前文所述两种表达方式进行计算，共设置以下2个计算工况：

工况一：考虑纯动力工况，粘弹性边界单元参数采用式(1)~式(3)进行计算^{[10 − 11]}，即阻尼矩阵与刚度矩阵成正比。

工况二：考虑纯动力工况，粘弹性边界单元参数采用本文提出的方法进行计算，即阻尼矩阵与集中质量矩阵成正比。

通过对比工况一和工况二的计算结果，来验证本文提出的粘弹性边界单元表示方式的计算精度。

图12所示为两种工况下坝顶点两向加速度时程对比。可以看出，采用两种表示方式的粘弹性边界单元，计算得到的坝顶点两向加速度时程整体上吻合良好。这表明使用与质量成正比的阻尼矩阵表示的粘弹性边界单元，可以较好的吸收坝体散射产生的外行波场。图13所示为两种工况下坝体大、小主应力包络对比。可以看出，采用两种表示方式的粘弹性边界单元，计算得到的坝体应力分布形态、应力水平与高应力区基本一致。

图  12  两种工况下坝顶两向加速度时程对比

Figure  12.  The comparison of acceleration at the dam crest in two cases

下载: 全尺寸图片 幻灯片

两个工况的计算结果吻合良好，这是因为：工况一中采用刚度比例阻尼矩阵等效一致阻尼器元件，即阻尼器元件连续均匀分布在地基截断边界表面，工况二中采用质量比例阻尼矩阵等效集中阻尼器元件，即阻尼器元件集中分布在地基截断边界的节点上，虽然两种等效边界单元阻尼矩阵表达形式存在较大差别(如式(4)与式(6)所示)，但二者均能等效粘弹性边界。

图  13  两种工况下坝体主应力对比

Figure  13.  The comparison of principal stress distribution in two cases

下载: 全尺寸图片 幻灯片

4   结论

本文使用与集中质量矩阵成正比的阻尼矩阵等效集中阻尼器元件，推导了一种基于与质量成正比的阻尼的粘弹性边界单元。通过某重力坝纯动力响应分析，验证所提出的粘弹性边界单元的计算精度；利用基于局部子系统传递矩阵谱半径的分析方法，研究了其在显式动力计算时的数值稳定性。具体结论为：

(1) 给出了使用与集中质量矩阵成正比的阻尼矩阵等效集中阻尼器元件时，粘弹性边界单元的参数计算方式。

(2) 与以往使用刚度比例阻尼矩阵等效一致阻尼器元件的粘弹性边界单元相比，基于与集中质量矩阵成比例的阻尼矩阵的优势是，可以保证传统中心差分法中系数矩阵的对角特性，有利于保持传统中心差分法的计算效率。

(3) 在显式动力计算数值稳定性方面，当粘弹性边界单元密度取内部介质密度时，无论是侧边子系统还是角点子系统，本文推导的基于与集中质量成正比的阻尼的粘弹性边界单元稳定性条件，均略优于以往使用的与刚度成正比的阻尼表示粘弹性边界单元的数值稳定性。特别地，当内部介质泊松比小于0.2，边界单元密度取内部介质密度时，传统基于刚度比例阻尼的粘弹性边界单元数值稳定性条件比内部介质更为严格；而本文所提出的基于与集中质量成正比的阻尼的粘弹性边界单元稳定性条件，始终比内部介质数值稳定性条件更宽松。

(4)通过半无限空间点源激励算例，验证了所提出与集中质量矩阵成正比的粘弹性边界单元的计算精度、数值稳定性。进一步，将其应用至某重力坝纯动力反应分析，可以看出使用两种粘弹性边界单元时，坝体主应力包络图、坝顶两向加速度时程图均吻合良好。

对于三维情况，同样可以按照本文提出的等效思路推导基于质量比例阻尼的三维等效粘弹性边界单元，有待进一步研究。