新型悬挂式单轨交通系统作为一种创新型交通方式，具备对地形条件的要求较低、建设周期短、采用环保清洁能源等多重优势。截至2023年1月，超过10座城市的旅游轨道交通项目建成并投入运营。悬挂式单轨交通系统已逐渐成为轨道交通未来发展的重要趋势之一^[1]。轨道梁结构作为悬挂式单轨交通系统的主要承力构件，通过纵横交错的加劲肋和箱板的焊接方式来连接各个部件，这种结构在列车车轮的反复负载下，焊缝区域容易出现应力集中。此外，在进行热切割和焊接过程中会不可避免的导致初始缺陷的生成^[2]，这些初始缺陷的产生很容易导致裂纹萌生或直接生成初始裂纹^[3]。在裂缝开始形成或初期扩展时，这些裂缝往往极小，以至于常规检测技术难以精确地发现它们。随着裂缝的不断发展和扩大，会显著降低结构的刚度，并有可能引起严重的安全问题和经济损失。因此，极需开发有效的疲劳寿命预测方法，以便对轨道梁结构的疲劳寿命进行预测，为其日常的维护与管理提供科学的支持，防止由于结构疲劳造成的工程事故。

国内外学者针对车辆-轨道梁相互作用与轨道梁疲劳问题展开了一系列研究。在轨道梁结构耦合振动相关研究方面，LYU等^[4]利用多体动力学分析软件SIMPACK软件建立了悬挂式单轨交通系统的车辆动力学分析模型，分析了车轮偏心对车辆垂直振动的影响。研究发现，当车辆速度提升至21 km/h时，车轮偏心会导致车体振动显著增加。在这种情况下，减少二系垂直刚度有助于降低由车轮偏心引发的振动；GUTAREVYCH^{[5 − 6]}通过建立考虑车辆横摆运动作用的悬挂式单轨交通系统车辆动力学模型，分析了列车自身的振动频率，并推导了悬挂式单轨列车的运动方程；李奇等^[7]基于开封悬挂式单轨示范线，开发了胶轮列车-钢轨道梁桥耦合振动分析程序，对列车走行性以及轨道梁桥的动力性能进行综合评估；李靖等^[8]以某旅游专线项目30 m跨度简支段为工程背景，利用有限元分析软件ANSYS创建了轨道梁的有限元模型，同时使用多体动力学分析软件SIMPACK来构建车辆模型。通过对SIMPACK与ANSYS进行联合仿真分析，得到了风荷载作用下悬挂式单轨系统车桥耦合振动特性；何庆烈等^{[9, 23 − 25]}以我国首条悬挂式单轨交通系统试验线为背景，开展了车桥耦合动力学试验并与有限元模型计算结果相结合，得到了在不同列车速度运行工况作用下的悬挂式单轨系统车桥耦合动力性能。

在轨道梁结构疲劳性能相关研究方面，YAMASAKI等^[10]以1/2缩尺悬挂式单轨交通系统曲线轨道梁模型为基础，开展了曲线轨道梁结构的静态和疲劳试验研究，研究得到了曲线轨道梁截面应力的分布情况，并指出了在曲线轨道梁设计过程中应重点关注的一些结构参数细节；刁璐通^[11]进行了采用波形腹板的新型悬挂式轨道梁结构部分足尺模型试验，研究了腹板与底板的T形焊接头处的疲劳损伤细节；张宁等^[12]在国外现有的悬挂式单轨结构与国内试验线轨道梁设计参数的基础上，采用有限元与理论计算相结合的方法对悬挂式轨道梁的主焊缝受力状态进行详细分析计算，对轨道梁主焊缝传力规律，并进行了焊缝的强度和疲劳校核；高玉强等^[13]通过建立ABAQUS钢桥面板节段模型，分析了横隔板围焊端和顶板-U肋焊缝两处的最不利荷载工况，得到了斜拉桥纵隔板形式和厚度对钢桥面板疲劳细节的影响；王占飞等^[14]基于扩展有限单元法，利用ABAQUS有限元软件建立了3U肋正交异性板数值分析模型，通过引入初始裂纹长度、面板厚度、应力比三个变量参数，预测了面板与U肋焊缝疲劳细节的疲劳裂纹扩展路径及其疲劳寿命。

上述研究进展对认知悬挂式单轨交通系统轨道梁结构在移动荷载作用下的疲劳强度与疲劳寿命的变化规律有参考价值，但未涉及在移动荷载最不利运行工况作用下的疲劳损伤特征，也未揭示在循环疲劳荷载下整桥跨轨道梁模型在最不利运行工况作用下的疲劳抗力。

基于此，本文以悬挂式单轨交通系统整桥跨轨道梁结构的缩尺模型作为试验样本。为确保悬挂式轨道梁结构在实际工程中的疲劳性能及疲劳寿命满足要求，课题组设计了该轨道梁结构的缩尺模型进行疲劳试验，着重对悬挂式单轨交通系统轨道梁结构在列车移动荷载作用下整桥跨缩尺模型的关键疲劳细节位置处的疲劳性能及疲劳寿命进行分析。最后，根据研究所得成果与相应规范，对悬挂式单轨交通系统轨道梁结构关键疲劳细节位置处的疲劳性能的疲劳性能进行了评估，为同类型轨道梁结构的设计与损伤检测提供了建议。

1   相似比推导

本研究利用静力结构模型来分析轨道梁的基础性能，以确保缩尺轨道梁模型与足尺轨道梁模型在静力特性和应力情况上保持一致。在静力结构缩尺模型设计中共考虑了8个主要参数，并应用相似原理中的相似第二定理，建立了物理相似准则：

式中：$\sigma$为列车应力；$P$为列车载荷；$\mu$为材料泊松比；$f$为轨道梁跨中挠度；$I$为轨道梁截面惯性矩；$E$为材料弹性模量；$L$为轨道梁长度；$T$为时间。

将与问题有关的变量量纲分解为$\left[ {FLT} \right]$的基本量纲系统，如表1所示。

由此得到缩尺轨道梁模型的物理量的${\bf\textit{π}}$矩阵，如表2所示。

表  1  各物理量的量纲矩阵

Table  1.  The dimensional matrix of each physical quantity

系数	${{\text{A}}_1}$	${{\text{A}}_2}$	${{\text{A}}_3}$	${{\text{A}}_4}$	${{\text{A}}_5}$	${{\text{A}}_6}$	${{\text{A}}_7}$	${{\text{A}}_8}$
量纲	$\sigma$	$E$	$\mu$	$f$	$I$	$P$	$L$	$T$
$F$	$1$	$1$	$0$	$0$	$0$	$1$	$0$	$0$
$L$	$- 2$	$- 2$	$0$	$1$	$4$	$0$	$1$	$0$
$T$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$1$

下载: 导出CSV 

| 显示表格

表  2  各物理量的${\text{π}}$矩阵

Table  2.  The ${\text{π}}$ matrix of each physical quantity

系数	${{\text{A}}_1}$	${{\text{A}}_2}$	${{\text{A}}_3}$	${{\text{A}}_4}$	${{\text{A}}_5}$	${{\text{A}}_6}$	${{\text{A}}_7}$	${{\text{A}}_8}$
量纲	$\sigma$	$E$	$\mu$	$f$	$I$	$P$	$L$	$T$
${{\textit{π}} _1}$	$1$	$0$	$0$	$0$	$0$	$- 1$	$2$	$0$
${{\textit{π}} _2}$	$0$	$1$	$0$	$0$	$0$	$- 1$	$2$	$0$
${{\textit{π}} _3}$	$0$	$0$	$1$	$0$	$0$	$0$	$0$	$0$
${{\textit{π}} _4}$	$0$	$0$	$0$	$1$	$0$	$0$	$- 1$	$0$
${{\textit{π}} _5}$	$0$	$0$	$0$	$0$	$1$	$0$	$- 4$	$0$

下载: 导出CSV 

| 显示表格

将上述矩阵的结果根据相似第二定理推导的参数，重新代入相应的相似准则中，得出剩余的5个无量纲数的相似准则为：

由相似准则式(3)可得：

相似比为：

由相似第三定理可知，将已确定的单值条件代入已求得的相似关系中可求得相似常数$\lambda$($\lambda$为原模型参数与缩尺模型参数之比)：

2   试验模型设计

根据试验模型设计基本原则和国内外试验模型设计经验，在前期研究的基础上，针对轨道梁结构走行面受列车轮载作用疲劳易损细节设计试验模型用于研究悬挂式单轨交通系统轨道梁结构的实际疲劳抗力。

悬挂式单轨交通系统最早出现于国外，经过长达100余年的发展历史，在近年中进入中国进行研究。目前中国悬挂式单轨线路多采用小车型系统，轨道梁内净截面尺寸宽780 mm~835 mm，高1100 mm~1250 mm，轨道梁截面形式多采用开口薄壁截面。考虑到本文中所选用的中车集团某型号列车轴重载荷，并总结过往国内外试验线结构形式^[15]。综合考虑后，在本文中选用选择轨道梁内净截面尺寸宽780 mm，高1100 mm的截面尺寸作为研究背景。

轨道梁缩尺试验模型的内廓尺寸宽为195 mm×275 mm，下翼缘板开口宽度60 mm，上翼缘板厚度6 mm，下翼缘板厚度8 mm，腹板厚度6 mm。所用钢材的弹性模量为206 GPa，泊松比为0.3，模型与原型的相似关系如表3所示。为更准确地模拟悬挂式轨道梁走行面板受车辆载荷作用下典型疲劳易损细节的实际受力状态，在实验模型顶板处开口，以便对走行面板进行模拟列车车轮实际加载。基于中车集团某型号列车，计算运行速度参数分别为10 km/h~70 km/h(每隔10 km/h)，设计轴重4.9 kN，列车编制为两编制，列车轴重载荷示意如图1所示。试验模型中各主要板件的厚度等参数根据前期相似比研究，设置为与实桥参数缩尺比例$\lambda = 4$，试验模型结构尺寸参数如图2。

表  3  模型与原型的相似关系

Table  3.  The similarity between model and prototype

项目	原型	模型
应力	1	1
载荷	16	1
泊松比	1	1
挠度	4	1
惯性矩	256	1
弹性模量	1	1
长度	4	1
时间	1	1

下载: 导出CSV 

| 显示表格

图  1  列车轴重载荷示意图

Figure  1.  Train axle load diagram

下载: 全尺寸图片 幻灯片

图  2  试验模型构造图

Figure  2.  Test model construction diagram

下载: 全尺寸图片 幻灯片

3   试验方案

3.1   加载方案

此前有学者研究发现，荷载加载面积、加载点之间的距离以及加载位置均会对各疲劳细节的应力产生影响，为了更准确地模拟实际车辆作用效应，参考前人对车轮作用的研究结果^[11]，换算得到加载面约为40 mm×20 mm。故本文疲劳试验采用荷载作用面积为40 mm(纵)×20 mm(横)的双点加载方式，加载点中心距为127.5 mm(净间距107.5 mm)。

纵桥向最不利加载位置根据有限元计算结果确定，加载条件采用模拟跨中车辆轮载局部受压状态对轨道梁走行面板进行加载，疲劳试验在辽宁省交通高等专科学校道路与桥梁工程系结构实验室完成，采用MTS电液伺服疲劳试验机进行疲劳加载，模型底部与支座之间设置为简支约束。为模拟车轮荷载，在分配梁底部设置垫块。加载时MTS疲劳试验机通过传力柱对轨道梁试验模型进行加载，如图3所示。

图  3  缩尺整桥跨疲劳试验模型

Figure  3.  Scaled bridge span fatigue test model

下载: 全尺寸图片 幻灯片

实际运行过程中设计满员最大轴重为4.9 t，空行轴重按3.5 t，综合考虑加载效率，采用增大应力幅的加速加载模式。缩尺试验模型采用加速工况进行加载，荷载幅取值为21.2 kN(最小荷载为5.3 kN，最大荷载为26.5 kN)，加载频率为1.5 Hz。通过有限元计算，在26.5 kN荷载作用下，有限元模型最大Mises应力(266 MPa)小于屈服应力(345 MPa)。

在正式加载前，采用50%最大荷载进行两次预加载，以消除试件的初始变形，并同时检查仪器是否正常工作。正式加载过程中，每隔10万次进行停机，检查模型各关键部位是否出现开裂或异常。

为确保原型与模型相似关系的正确性，通过对静载过程中所采集的位移数据与模拟所得的结果进行对比分析，所得应力、位移对比结果均与相似比例接近。原型模拟静载位移与模型试验静载位移比对结果如表4所示，足尺模型与缩尺模型在静载试验下的位移及应力云图对比见图12。

表  4  原型模拟静载位移与模型试验静载位移

Table  4.  Static displacement simulated by prototype and static displacement tested by model

位置	模型试验竖向位移/mm	原型模拟竖向位移/mm
0号支座	0.51	/
−1/4跨径	5.11	18.92
−400 mm	6.53	24.16
跨中	7.82	28.85
400 mm	6.58	24.21
1/4跨径	5.13	18.98
1号支座	0.52	/

下载: 导出CSV 

| 显示表格

3.2   测点布置及测试方案

为保证试验结果的可靠性，本文采用组合式监测方法对同一参数采用多种量测方法相互验证。根据试验加载方案，在关注的疲劳易损部位布置应变测点、位移传感器及加速度传感器以监测关键细节疲劳裂纹的产生，测点布置如图4、图5所示。通过在沿轨道梁X轴方向−1/4跨径、−400 mm、−200 mm、跨中、200 mm、400 mm、1/4跨径位置处分别设置应力、位移传感器及加速度传感器并在0号支座与1号支座处设置支座沉降测试点。在下翼缘板的上下表面设置单向应变片测试点用以了解走形面板在跨中车辆轮载局部受压状态下的纵向受力情况；使用三轴45°应变花来研究焊缝疲劳敏感细节周围的应力分布，应变花的相互垂直的两个方向分别布置为垂直于焊缝和平行于焊缝，为避免焊缝应力的影响，在对焊缝的应力状态进行采集时，选择将应变花测试点设置在垂直于焊缝3 mm位置处；在轨道梁下翼缘板的底面与腹板的侧面分别设置竖直与水平位移测试点，用以测量轨道梁在不同循环次数下的位移响应情况，数据采集使用扬州晶明公司生产的JM 3818无线静态应变仪，试验数据采集过程如图6。

图  4  测试点设置示意图

Figure  4.  Schematic diagram of strain and displacement test points

下载: 全尺寸图片 幻灯片

图  5  测试点布置示意图

Figure  5.  Layout of test points

下载: 全尺寸图片 幻灯片

图  6  试验数据采集过程示意图

Figure  6.  Schematic diagram of test data acquisition process

下载: 全尺寸图片 幻灯片

4   试验结果及分析

4.1   疲劳开裂形态

经过200万次疲劳加载，试验模型共出现了2条疲劳裂纹(记为1~2#裂纹)。疲劳裂纹发现过程如下：①疲劳加载至约145万次，在跨中纵肋与下翼缘板底面相接位置处观察到第一条裂纹(1号裂纹)，起裂点位于跨中中心线偏右30 mm，向上下两侧扩展；②当疲劳加载至约155万次，在跨中位置腹板与下翼缘板顶面相接位置处观察到2号裂纹。起裂点位于跨中中心线偏右48 mm，向上下两侧扩展。裂缝开裂形态如图7、图8。

图  7  1#裂纹开裂形态

Figure  7.  1# crack cracking pattern

下载: 全尺寸图片 幻灯片

图  8  2#裂纹开裂形态

Figure  8.  2# crack cracking pattern

下载: 全尺寸图片 幻灯片

4.2   疲劳裂纹开裂时刻

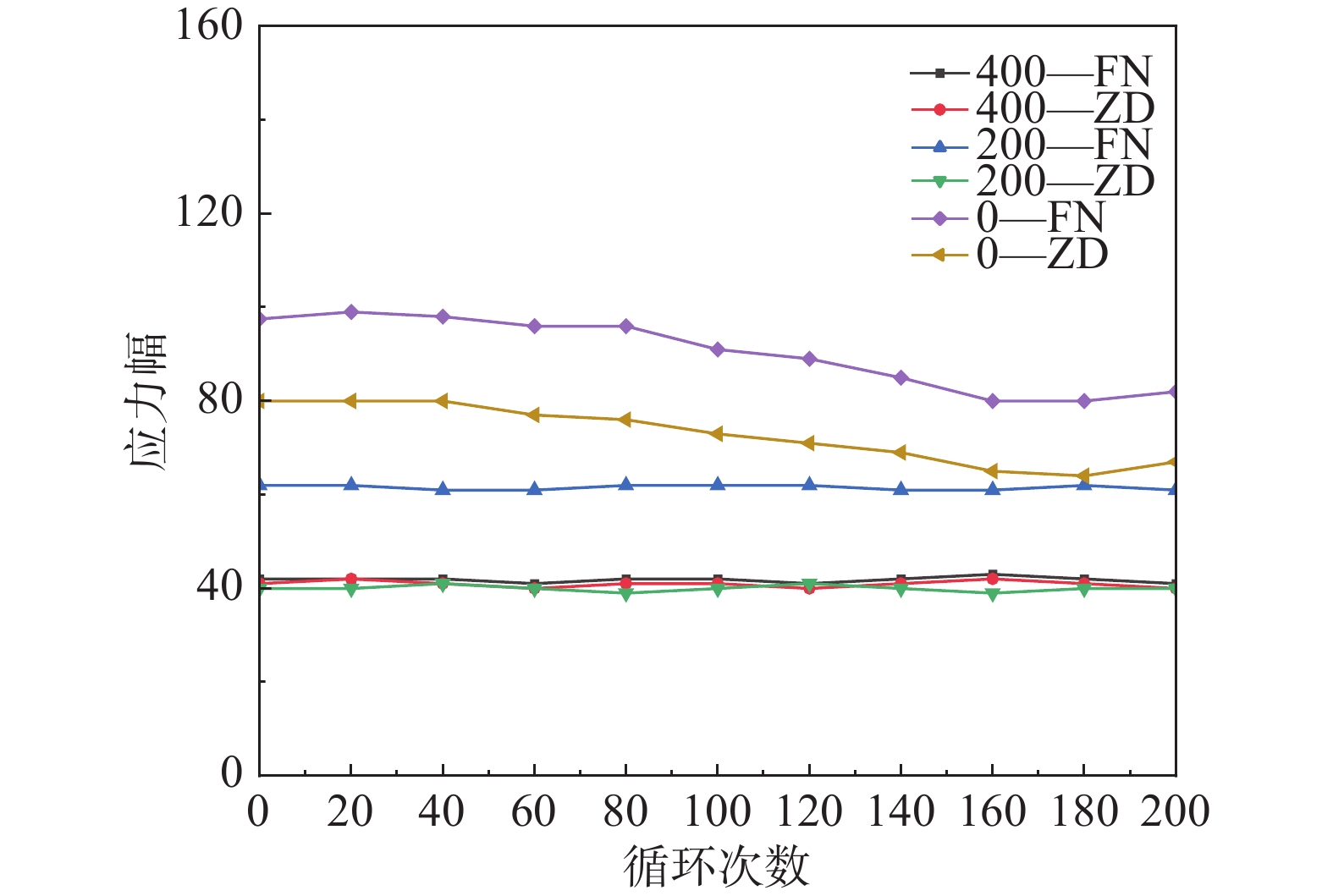
基于各关键应变片与加速度测试点所测数据，对各试验模型的疲劳裂纹开裂时刻进行分析。疲劳试验过程中各附近关键测点应力幅随作用次数变化曲线如图9所示。

图  9  应力幅随作用次数变化曲线

Figure  9.  Stress amplitude varies with the number of action

下载: 全尺寸图片 幻灯片

对于1#裂纹，由图10 (a)可知，1#裂纹附近关键测点的应力幅变化总体趋势为先略微上升后下降。在前70万次加载过程中，应力无显著变化，但在70万次加载过后，随着加载作用次数的增加，应力幅不断下降，当加载至150万次时，应力幅下降超过了10%。因此，判定的1#裂纹起裂于疲劳加载150万次左右。

图  10  裂纹处测点应力幅随作用次数变化示意图

Figure  10.  Diagram of variation of stress amplitude at measuring point of crack with frequency of action

下载: 全尺寸图片 幻灯片

对于2#裂纹，由图10 (b)可知，2#裂纹附近关键测点的应力幅变化总体趋势为先稳定后下降。在前70万次加载过程中，应力无显著变化，但在70万次加载过后，随着加载作用次数的增加，应力幅不断下降，当加载至160万次时，应力幅下降超过了10%。因此，判定的2#裂纹起裂于疲劳加载160万次左右。

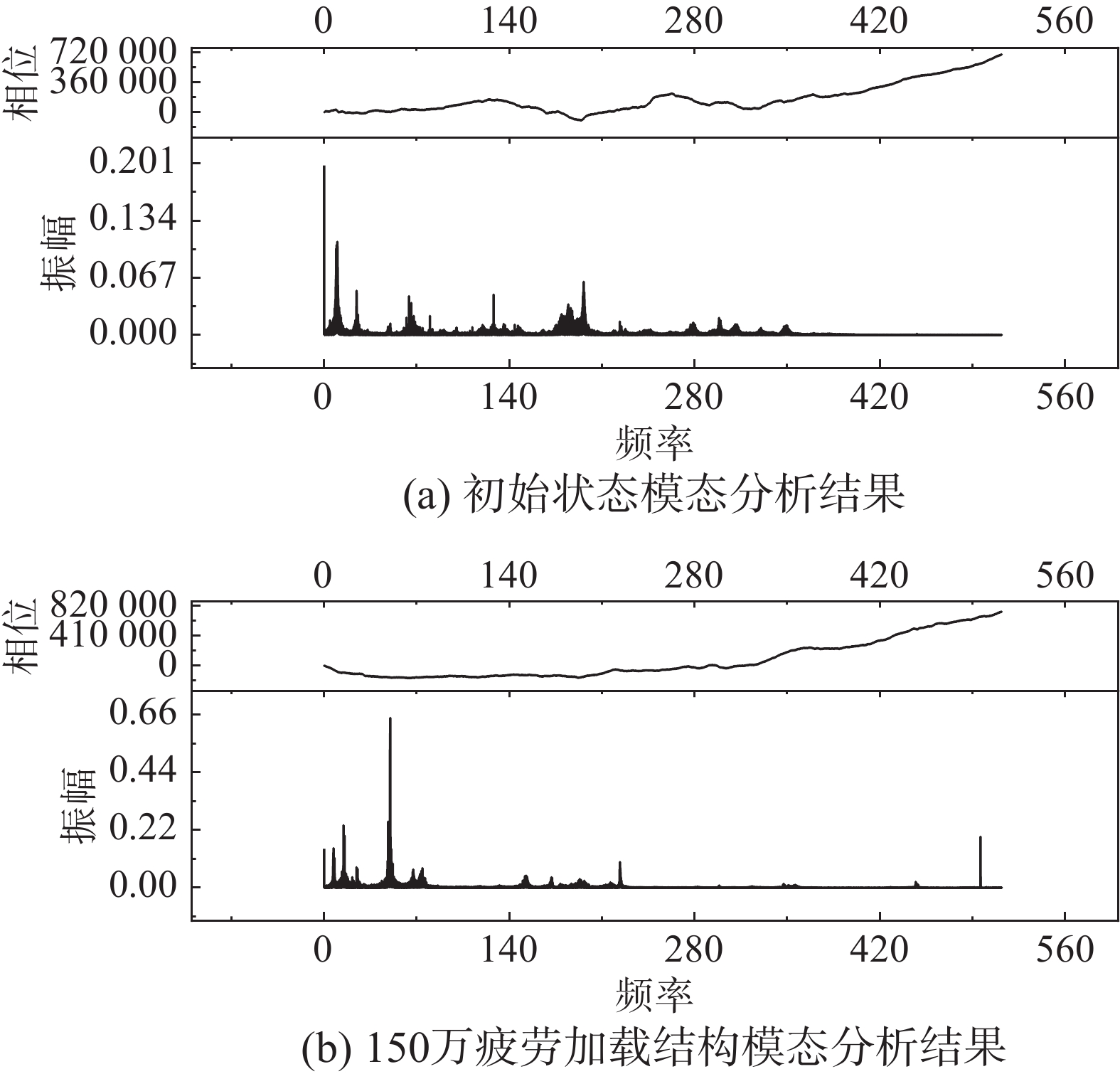
结合模态分析方法，对比11 (a)、图11 (b)可知，在前150万次疲劳加载过程中结构跨中测试点固有频率由10.04 HZ下降至7.31 HZ，振幅由0.11 mm增大至0.15 mm。因此通过模态分析方法判定结构在疲劳加载至150万次时发生损伤。

对于试验模型±200 mm与±400 mm位置处，在整个加载过程中未发生疲劳开裂。

通过试验模型疲劳裂纹开裂过程对比分析发现：①在疲劳开裂前，关键测点的应力幅均无显著变化，但疲劳开裂后，焊趾位置及新型悬挂式轨道梁结构疲劳易损部位的应力幅的关键测点应力幅随作用次数的增加而减小；疲劳易损部位的应力幅的测点应力幅应力幅先略微增大，主要是受附近裂纹产生导致的应力重分布影响所致，当裂纹扩展到该测点附近时，应力幅开始下降。②在疲劳过程中其他位置处的疲劳易损部位的应力幅在未达到其裂纹萌生疲劳寿命时，其应力幅并不会发生显著变化。

图  11  结构模态分析结果

Figure  11.  Structural modal analysis junction

下载: 全尺寸图片 幻灯片

5   移动荷载作用下的轨道梁动力学仿真分析

5.1   足尺分析模型建立

为验证由相似设计方法设计的缩尺模型的相似比及各项参数的可行性。通过有限元建模仿真的方法，建立缩尺模型与原模型，并分别施加对应的载荷和相同的约束方式，对其跨中挠度与应力分布情况进行对比，足尺模型与缩尺模型在静载试验下的位移及应力云图对比见图12。模型材料均采用Q345qD，弹性模量210 GPa，泊松比0.3，密度7.85 t/m³。设置全局网格尺寸为10 mm。由于列车在运行过程中采用实心橡胶轮胎，因此选择加载印记面为矩形。

由计算结果可知，原模型与缩尺模型在各自加载工况下，跨中挠度比接近缩尺比例且应力分布情况与大小也十分接近，证明了缩尺模型代替足尺模型进行后续试验研究的合理性。为后续研究提供了依据。

为确定轨道梁结构在列车移动荷载下的最大应力幅，基于ANSYS Workbench瞬态动力学分析模块对轨道梁结构进行移动荷载分析，步骤数量设置为50步。列车运行时速10 km/h~70 km/h工况下的位移计算结果见表5，移动荷载作用下足尺模型最大位移情况如图13、图14所示。

图  12  足尺模型与缩尺模型静载试验的位移、应力对比示意图

Figure  12.  Comparison diagram of displacement and stress in static load test between full-scale model and scaled model

下载: 全尺寸图片 幻灯片

表  5  10~70 km/h工况下的位移计算结果

Table  5.  Calculation results of displacement under the condition of 10~70 km/h

工况	足尺模型竖向 位移$\Delta {\text{y/mm}}$	足尺模型水平 位移$\Delta {\text{x/mm}}$	缩尺模型竖向 位移$\Delta {{\text{y}}_1}{\text{/mm}}$	缩尺模型水平 位移$\Delta {{\text{x}}_1}{\text{/mm}}$
自重	4.86	0.32	1.21	0.079
10 km/h	18.71	2.72	4.67	0.67
20 km/h	18.05	2.63	4.51	0.66
30 km/h	19.13	2.73	4.78	0.68
40 km/h	17.83	2.63	4.46	0.66
50 km/h	17.89	2.55	4.47	0.63
60 km/h	18.31	2.68	4.58	0.67
70 km/h	18.55	2.58	4.64	0.65

下载: 导出CSV 

| 显示表格

图  13  足尺模型移动荷载下最大位移情况(30 km/h)

Figure  13.  Maximum displacement of full-size model under moving load (30 km/h)

下载: 全尺寸图片 幻灯片

图  14  缩尺模型移动荷载下最大位移情况(30 km/h)

Figure  14.  Maximum displacement under moving load of scaled model (30 km/h)

下载: 全尺寸图片 幻灯片

由表5与何庆烈^[16]在10 km/h~60 km/h工况下的动力测试结论可知与在列车移动荷载作用下的轨道梁动力响应受到速度的影响比较明显，由于轨道梁的固有频率比较低，在较低的车速工况作用下的动力响应存在较大波动。基于以上结论，在本文中取列车编组30 km/h下的运行工况作为最不利运行工况进行后续分析，悬挂式单轨车桥系统在重载工况下的动力性能测试结果见表6。

表  6  列车重载通过直线桥梁时的车辆及轨道梁桥动力测试结果(最大值)

Table  6.  Dynamic test results of vehicle and rail beam bridge when heavy trains pass straight Bridges (maximum)

运行速度/(km·h−1)	跨中位移/mm			墩顶位移/mm			跨中加速度/g			墩顶加速度/g		轨道梁最大竖向梁端转角/rad	位移动力放大系数
	垂向	横向		垂向	横向		垂向	横向		垂向	横向
10	28.0	18.1		14.7	27.6		0.050	0.058		0.022	0.042	1.64‰	1.09
20	27.8	17.9		14.7	28.3		0.098	0.103		0.050	0.068	1.62‰	1.08
30	29.0	18.8		15.1	29.1		0.145	0.190		0.073	0.091	1.72‰	1.13
40	28.5	18.5		15.3	28.6		0.178	0.240		0.082	0.156	1.68‰	1.11
50	27.6	17.6		15.6	27.9		0.190	0.300		0.143	0.178	1.61‰	1.07
60	28.6	18.6		15.6	28.0		0.200	0.340		0.165	0.195	1.69‰	1.11

下载: 导出CSV 

| 显示表格

5.2   轨道梁走行面板应力分析

根据车辆载荷谱，在ANSYS Workbench软件中编写移动荷载加载步，列车编组前轴走行面一端进入，后轴从走行面另一端离开。加载工况按前文中最大移动荷载最大动力响应值工况(30 km/h)，每个荷载步设置为0.015 s向前移动125 mm进行加载。通过有限元计算结果可知：列车编组在移动过程中，轨道梁走行面板应力随列车位置的变化而变化，跨中腹板与下翼缘板连接与下翼缘板连接处的最大应力幅$\Delta {\sigma _s}$分别为38.08 MPa与39.55 MPa；±200 mm腹板与下翼缘板连接处与±200 mm纵肋与下翼缘板连接处的最大应力幅$\Delta {\sigma _{\max }}$分别为37.13 MPa与38.01 MPa。

5.3   模型局部应力分析

为了确定缩尺试件对于结构应力细节的影响，将足尺模型和缩尺模型的局部焊趾特征参数分别进行有限元分析，建立节段有限元实体模型，对试件加载面处施加大小按照相似常数分别施加16 000 N和1000 N的橡胶轮胎印记面压力，并在焊缝附近对网格进行了加密，有限元分析工况见表7，有限元模型如图15所示，分析结果如图16所示。

表  7  局部应力分析工况

Table  7.  Minimum fatigue life of each weld in X axis direction of the track beam

模型	荷载/N
缩尺	1000
足尺	16000

下载: 导出CSV 

| 显示表格

图  15  局部应力分析模型

Figure  15.  Local stress analysis model

下载: 全尺寸图片 幻灯片

图  16  模型局部应力分布示意图

Figure  16.  Diagram of local stress distribution of the model

下载: 全尺寸图片 幻灯片

在模型跨中位置处，分别模型沿X方向分别提取了一定距离内的应力大小，得到焊趾部位局部应力分布曲线，见图17所示。

从图17中可以看出，在焊趾部位(x=0 mm)的缩尺模型局部应力分布曲线与足尺模型局部应力分布曲线的趋势相同，靠近焊趾部位的缩尺模型局部应力比足尺模型小，随着距离增大，这种差异逐渐减小。但是二者间的应力水平差异并不明显，二者靠近焊趾部位应力差异最大，应力差异处于7%范围内。

图  17  模型局部应力分布曲线

Figure  17.  Model local stress distribution curve

下载: 全尺寸图片 幻灯片

若单纯考虑焊缝的几何特征，则有限元分析结果表明缩尺结构的应力集中程度略低于足尺结构但两者差别不大。同时，在名义应力测点位置两者的曲线几乎重合，说明进行结构的缩尺试验设计对试件名义应力大小的无明显影响。

5.4   缩尺模型焊缝疲劳寿命分析

焊接结构疲劳破坏一般始发于焊趾处，从断裂力学的角度，影响焊缝裂纹扩展速度的主要因素是从焊趾处开始，沿板材垂直截面上的全部应力分布状态，而不只是焊趾处的表面应力^[17]。TONG等^[18]在研究焊缝开裂机理时率先提出了结构应力法，它是基于焊接结构疲劳强度问题的特殊性和力学原理而定义的一种应力，对焊趾周围单元节点力的分布进行研究，将单元节点力等效为单元边界上的线载荷，避免了由有限元网格尺寸引起的计算结果误差，提高了计算结果的准确性，能够准确反映变截面处应力集中位置的应力情况。结构应力的计算可由式(7)表示：

式中：$t$为板厚度；${f_y}$与${m_x}$分别为焊线处的线力与线矩。

若将一段焊缝划分为$n - 1$个单元时，节点编号为由$1\sim n$，焊线上的各节点之间的距离为${l}_{1}、{l}_{2}、{l}_{3}、\cdots 、{l}_{n-1}$，根据力的平衡方程，各节点力${F_{yn}}$与各节点线力${f_{yn}}$的对应关系为：

同理，各节点力矩${M_x}$与各节点线矩${m_x}$有相同的表达形式。当有$n$个节点在相同的单元厚度$t$的情况下，各节点的结构应力${\sigma _n}$，以及各节点力${f_{yn}}$和力矩${M_{xn}}$可用矩阵方程表示为：

为考察焊接轨道梁结构在移动荷载作用下的焊接接头的力学行为与焊缝疲劳寿命，建立直线段轨道梁实体单元缩尺分析模型，下翼缘板下方焊脚尺寸采用有效焊高3.5 mm的双面角焊缝，其余焊缝焊脚尺寸均采用有效焊高3 mm的双面角焊缝，通过有限元分析软件ANSYS Workbench与疲劳分析软件Ncode进行联合分析。

由如图18分析结果可知，腹板与底板焊缝的上下焊趾的最大主应力${\sigma _{\max }}$在轨道梁结构跨中区域的数值较大，故在跨中区域与与跨中±200 mm跨径位置处共选取12个点位进行应力分析，分别为：腹板与下翼缘板相接跨中位置处的内外焊趾(S1、S2)，腹板与下翼缘板相接位置−200 mm与200 mm位置处的内外焊趾(S3-1、S3-2、S4-1、S4-2)，下翼缘板与纵向加劲肋相接跨中位置处的内外焊趾(S7、S8)，下翼缘板与纵向加劲肋相接位置−200 mm与200 mm位置处的内外焊趾(S9-1、S9-2、S10-1、S10-2)，沿轨道梁X轴方向的焊缝最小疲劳寿命分析结果如表8。

图  18  沿轨道梁X轴的典型焊缝疲劳寿命

Figure  18.  The maximum principal stress of a typical weld along the X-axis of a track beam

下载: 全尺寸图片 幻灯片

表  8  轨道梁X轴方向的各焊缝疲劳寿命

Table  8.  Minimum fatigue life of each weld in X axis direction of the track beam

焊缝位置	最小疲劳寿命/万次
S1	288.3
S2	150.8
S3-1	687.2
S3-2	632.7
S4-1	682.1
S4-2	630.3
S7	152.5
S8	171.3
S9-1	428.1
S9-2	310.1
S10-1	424.6
S10-2	308.3

下载: 导出CSV 

| 显示表格

结合上文中试验过程中单向应变片与三轴应变花所测试验数据与本节所关注的疲劳易损部位的疲劳寿命有限元模拟进行对比可以看出，对试验模型在200万次试验中所得到的疲劳寿命与模拟拟合较好，跨中关键测点在前200万次疲劳过程中发生开裂时刻误差未超过5%。

6   轨道梁疲劳性能分析

目前对于悬挂式单轨轨道梁构造细节疲劳失效判据尚未有明确的统一，故本文根据Eurocode 3规范^[19]的规定：在循环作用次数达到$N = 2 \times {10^6}$次时，该疲劳细节类型为疲劳强度；循环作用次数达到$N = 5 \times {10^6}$次时，该疲劳细节类型为常幅疲劳极限；循环作用次数达到$N = 1 \times {10^8}$次时，该疲劳细节类型为疲劳截止极限。当所有应力水平都未超过特定细节的常幅疲劳极限，可以认为结构会具有无限的使用寿命，无需做进一步的疲劳分析；而对于低于特定疲劳截止极限的应力循环，可以不予考虑，但超出这一极限的应力循环则必须进行疲劳评估。

Eurocode 3规范中规定，对于名义应力谱，其对应的疲劳强度曲线为：

式中：$\Delta {\sigma _i}$为应力幅水平；$m$为S-N曲线的斜率绝对值；${N_i}$为$\Delta {\sigma _i}$对应的疲劳寿命(循环次数)；$\Delta {\sigma _{\text{D}}}$为常幅疲劳极限。若应力幅水平$\Delta {\sigma _i}$高于$\Delta {\sigma _{\text{D}}}$，则$m = 3$；若应力幅水平$\Delta {\sigma _i}$低于$\Delta {\sigma _{\text{D}}}$，则$m = 5$。$\Delta {\sigma _{\text{L}}}$为疲劳截至限，若应力幅水平$\Delta {\sigma _i}$低于$\Delta {\sigma _{\text{L}}}$，则结构不会产生疲劳损伤。

在本文加速疲劳工况下，以下针对试验模型疲劳开裂细节，采用名义应力法对其开展200万次循环疲劳强度计算与500万次循环常幅疲劳极限计算及寿命评估，利用式(11)、式(12)取$m = 3$将实测应力幅转换为200万次循环所对应的疲劳强度与500万次循环所对应的常幅疲劳极限^{[20, 21]}。

式中：$\Delta {\sigma _{\text{C}}}$为疲劳强度；${n_i}$与$\Delta {\sigma _i}$分别为第$i$个引起损伤的应力幅值和所对应的作用次数；${N_{\text{C}}}$为疲劳强度$\Delta {\sigma _{\text{C}}}$所对应的作用次数，取200万次。

式中：$\Delta {\sigma _{\text{D}}}$为常幅疲劳极限；${n_i}$与$\Delta {\sigma _i}$分别为第$i$个引起损伤的应力幅值和所对应的作用次数；${N_{\text{D}}}$为常幅疲劳极限$\Delta {\sigma _{\text{D}}}$所对应的作用次数，取500万次。

Miner线性累积损伤理论：

根据Miner理论，在${n_i}$个循环的变幅应力幅$\Delta {\sigma _i}$作用下造成的疲劳损伤为：

式中：$D$与${D_i}$分别为总损伤与第$i$个应力幅值引起的损伤；$N$为列车轮载作用次数；$\Delta {\sigma _s}$为轨道梁动力学分析中进行移动荷载加载下计算所得的应幅。

此前已有专家学者针对不同墩高结构形式与不同曲线半径的直线悬挂式轨道梁结构的疲劳性能进行了深入的研究^{[15, 22]}。研究结果发现，墩高对于直线段轨道梁结构的疲劳性能影响不大，轨道梁结构的竖弯弯曲应力为48.3 MPa，竖弯疲劳容许应力为82.9 MPa；曲线段轨道梁结构的疲劳应力随着曲线半径的增大而减小，疲劳容许应力为71.9 MPa。

在本文200万次加速试验加载工况下，轨道梁试验模型等效200万次疲劳强度、等效500万次常幅疲劳极限、有限元模拟中的最大应力幅及换算实桥等效疲劳寿命如表9所示。

对比前人的研究结果发现，轨道梁结构关键连接处焊趾对应主导疲劳开裂模式下的最小疲劳极限强度低于整体疲劳强度。

在本文加速疲劳试验加载工况条件下试验结果表明：

1)轨道梁主导疲劳开裂模式为：跨中腹板与下翼缘板连接处焊趾开裂，对应的疲劳强度分别为89.59 MPa；跨中纵肋与下翼缘板连接处焊趾开裂，对应的疲劳强度分别为70.52 MPa；

2)跨中关键连接处焊趾疲劳寿命分别145万次、155万次；其余位置关键连接处焊趾均未开裂，基于Eurocode 3规范规定200万次循环常幅疲劳极限验算结果可知关键连接处关注点的等效疲劳分别为2605.06万次与1436.47万次；

表  9  轨道梁试验模型疲劳性能

Table  9.  Fatigue performance of track beam test model

关注点	疲劳强度 $\Delta {\sigma _{\text{C}}}/{\text{MPa}}$	常幅疲劳极限 $\Delta {\sigma _{\text{D}}}/{\text{MPa}}$	最大应力幅 $\Delta {\sigma _{{\text{max}}}}/{\text{MPa}}$	验算结果	等效疲劳寿命/万次
跨中腹板与下翼缘板连接处	89.59	66.02	38.08	$\Delta {\sigma _{\text{D}}} {\leqslant} \Delta {\sigma _{{\text{max}}}}$	2605.06
跨中纵肋与下翼缘板连接处	70.52	51.96	36.55	$\Delta {\sigma _{\text{D}}} {\leqslant} \Delta {\sigma _{{\text{max}}}}$	1436.47

下载: 导出CSV 

| 显示表格

7   结 论

本研究通过对新型悬挂式单轨交通系统的轨道梁结构进行缩尺模型的疲劳试验，对轨道梁的有限元模型进行分析，采用名义应力法对关键的疲劳易损部位的疲劳寿命进行计算并与前人学者的研究结论进行对比，主要得出以下结论：

(1)在本试验加载工况下，轨道梁结构关键连接处焊趾对应主导疲劳开裂模式下的最小疲劳极限强度为70.52 MPa；与现有悬挂式单轨轨道梁疲劳研究结论进行比对发现，关键连接处焊趾对应主导疲劳开裂模式下的最小疲劳极限强度低于整体强度，建议在管养过程中对焊缝位置进行重点检查。

(2)通过轨道梁结构疲劳有限元分析，得到了轨道梁结构各关键焊趾位置处疲劳寿命，经分析得理论计算疲劳寿命与试验疲劳寿命误差未超过5%。

(3)通过轨道梁结构有限元分析，得到轨道梁跨中关键焊趾位置处的最大应力幅分别为38.08 MPa和36.55 MPa。

(4)基于Eurocode 3规范规定，轨道梁跨中关键焊趾位置处的最大应力幅均小于常幅疲劳极限，等效疲劳寿命分别为2605.06万次与1436.47万次；即桥梁在正常服役期间不会发生疲劳破坏。

(5)本文重点针对缩尺直线段轨道试验梁进行200万次疲劳试验的相关成果进行了阐述。由于时间经费有限，文中未尽之处良多，后续将对本文所研究内容进行深入研究。文中对新型悬挂式单轨交通系统曲线段轨道梁结构的疲劳强度、疲劳寿命尚未涉及，笔者后续将继续对曲线段轨道梁结构在列车离心力、摇摆力作用下的疲劳性能进行进一步研究。