环肋圆柱壳是潜艇、潜水器等水下工程产品中广泛应用的耐压结构形式，因兼具优异的受力特性、空间利用率和加工性能，一直以来受到水下工程产品开发人员的关注和研究^{[1 − 5]}。国内围绕环肋圆柱壳结构应力和稳定性分析问题，也已有不少相关研究的经典著作^{[6 − 7]}。

在静水压力作用下，环肋圆柱壳结构传统的应力分析方法是将圆柱壳化为两端刚性固定在弹性支座上的复杂弯曲弹性基础梁来研究，目前各国潜水器等规范均采用了这种力学模型来计算环肋圆柱壳的应力^{[8 − 12]}。所谓的弹性支座，是假定在肋骨横剖面上产生一个相等的挠度和相等的应力，实质上是假定肋骨的形心与壳板形心重合。对于一些采用大肋骨加强的圆柱壳结构，尤其是一些布置特大肋骨的情形，这种不考虑肋骨形心偏离影响及内、外肋骨差异的假定显然是不合理的。朱邦俊等^[13]提出一种考虑肋骨偏心的环肋圆柱壳应力分析方法，将环肋圆柱壳分解为肋骨腹板(平面应力的二维环板)、肋骨翼板(受线均布力的一维圆环)和圆柱壳体三部分，可以较精确地求解圆柱壳板，以及内、外肋骨各部位的应力。不论是传统的应力分析方法，还是朱邦俊等^[13]提出的方法，其本质上都将圆柱壳化为双向应力状态的复杂弯曲梁，忽略了中曲面上法向正应力的影响；同时，也都将肋骨面板视为单向应力状态，极其简化了肋骨面板作为环壳的复杂弯曲问题。在潜艇、潜水器等传统结构特征和设计参数范畴，这些简化引起的计算误差是很小的，可以适应工程应用要求。但是，随着深海技术的发展，水下工程产品的应用深度越来越深，一些深海无人系统的应用深度往往达几千米以深^{[14 − 16]}，静水压力载荷大小与耐压结构材料强度相比将达10%以上；同时，为保证耐压结构强度，结构设计厚度将远超传统薄壳结构范畴^{[17 − 18]}(传统薄壳结构t/R一般远小于5%，而大深度的耐压结构t/R将达到或超过10%)；另外，有时受限于总体布置等原因，导致环肋圆柱壳不得不采用矮宽型肋骨加强的特殊情形。显然，这些环肋圆柱壳的新设计特征明显不符传统的双向应力状态假设。

为研究分析新结构设计特征下的环肋圆柱壳应力，本文提出一种新的力学模型，利用轴对称平面问题分析方法和基于三向应力状态的弯曲微分方程，推导分析了环肋圆柱壳的三维应力计算方法，并以具有大深度、大厚度、矮宽型肋骨等结构设计特征的环肋圆柱壳为应用算例进行比较分析。

1   环肋圆柱壳的简化力学模型

1.1   结构特征符号

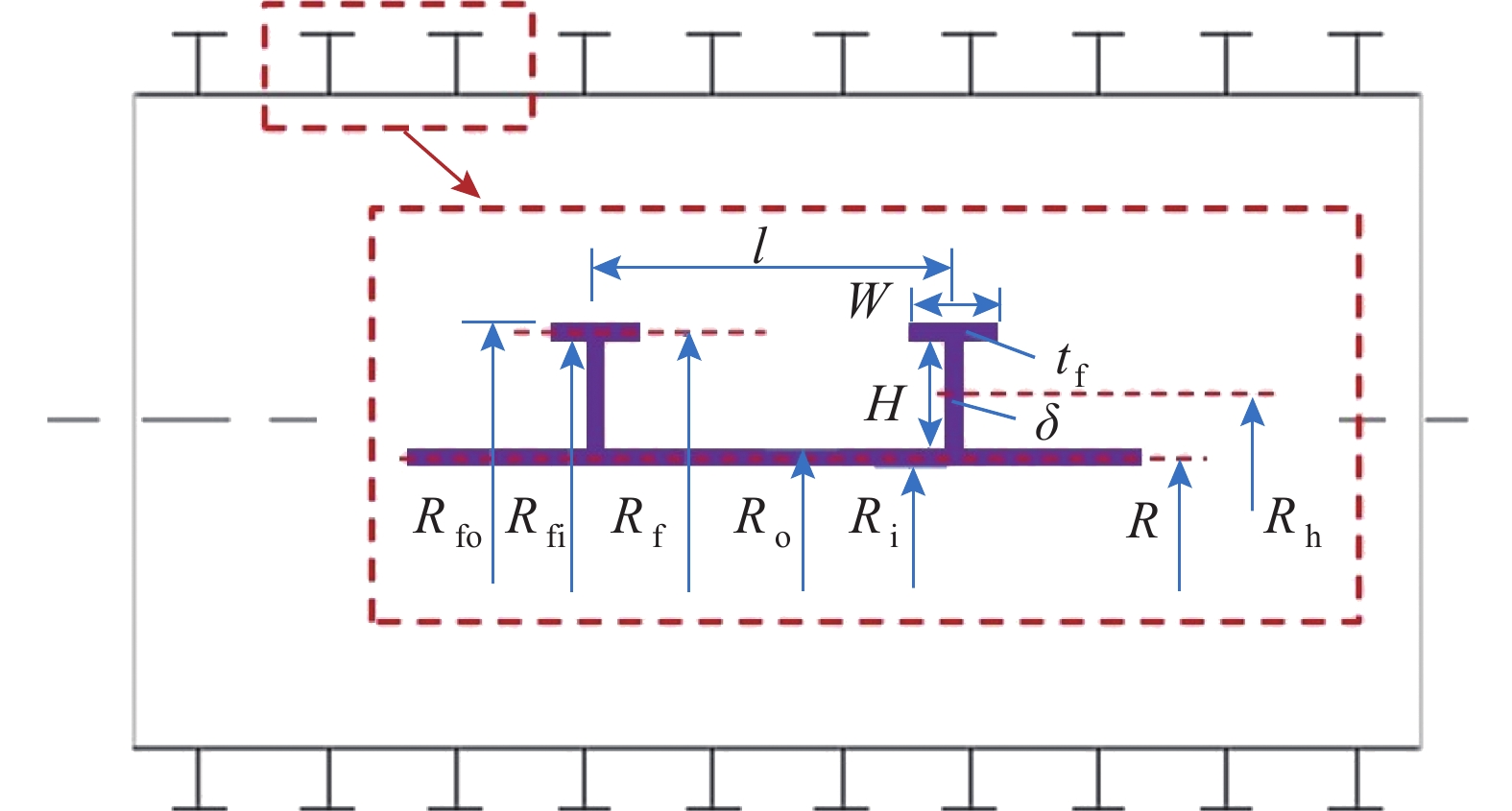
环肋圆柱壳的T型肋骨一般采取等间距布置，如图1所示，为便于分析，定义结构特征符号为：圆柱壳内半径为${R_{\text{i}}}$，外半径为${R_{\text{o}}}$，中面半径为$R$，壳厚度为$t$；T型肋骨的腹板高度为$H$，厚度为$\delta$，高度形心对应的半径为${R_{\text{h}}}$；肋骨面板宽度为$W$，厚度为${t _{\text{f}}}$，面板壳内外缘对应的半径为${R_{{\text{fo}}}}$、${R_{{\text{fi}}}}$，中面对应的半径为${R_{\text{f}}}$；相邻肋骨之间的间距为$l$；材料的弹性模量为$E$，泊松比为$\mu$。

图  1  环肋圆柱壳结构示意图

Figure  1.  Ring-stiffened cylindrical shell structure

下载: 全尺寸图片 幻灯片

为区分肋骨内外布置，定义肋骨内外布置系数$F$，当外肋骨时$F = 1$，内肋骨时$F = - 1$。因此有结构参数几何关系式${R_{\text{i}}} = R - 0.5t$、${R_{\text{o}}} = R + 0.5t$、${R_{\text{h}}} = R + 0.5F\left( {t + H} \right)$、${R_{{\text{fi}}}} = {R_{\text{f}}} - 0.5F{t _{\text{f}}}$、${R_{{\text{fo}}}} = {R_{\text{f}}} + 0.5F{t _{\text{f}}}$、${R_{\text{f}}} = R + F\left( {0.5t + H + 0{\text{.5}}{t _{\text{f}}}} \right)$。

1.2   简化力学模型

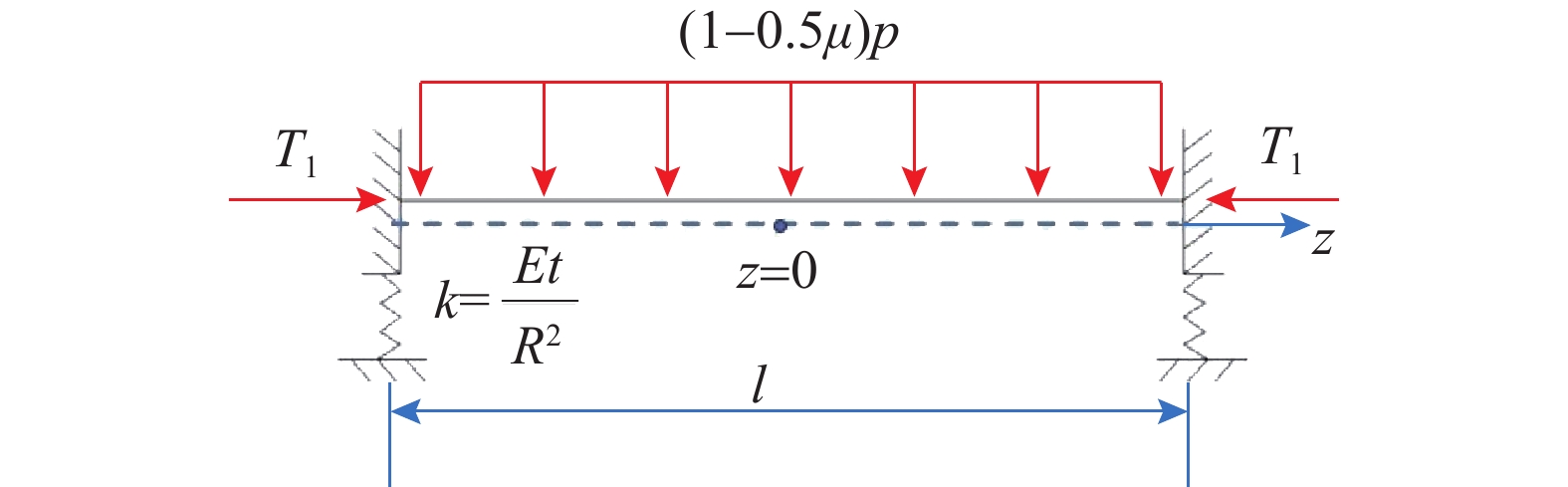
传统环肋圆柱壳结构力学模型^[6]将圆柱壳简化为弹性基础梁、肋骨视为弹性支座来进行分析，并将作用于圆柱壳表面的静水压力等效为弯曲梁中面上的径向力$(1 - 0.5\mu )p$，如图2所示。

图  2  传统环肋圆柱壳结构力学模型

Figure  2.  Traditional mechanical model of ring-stiffened cylindrical shell structure

下载: 全尺寸图片 幻灯片

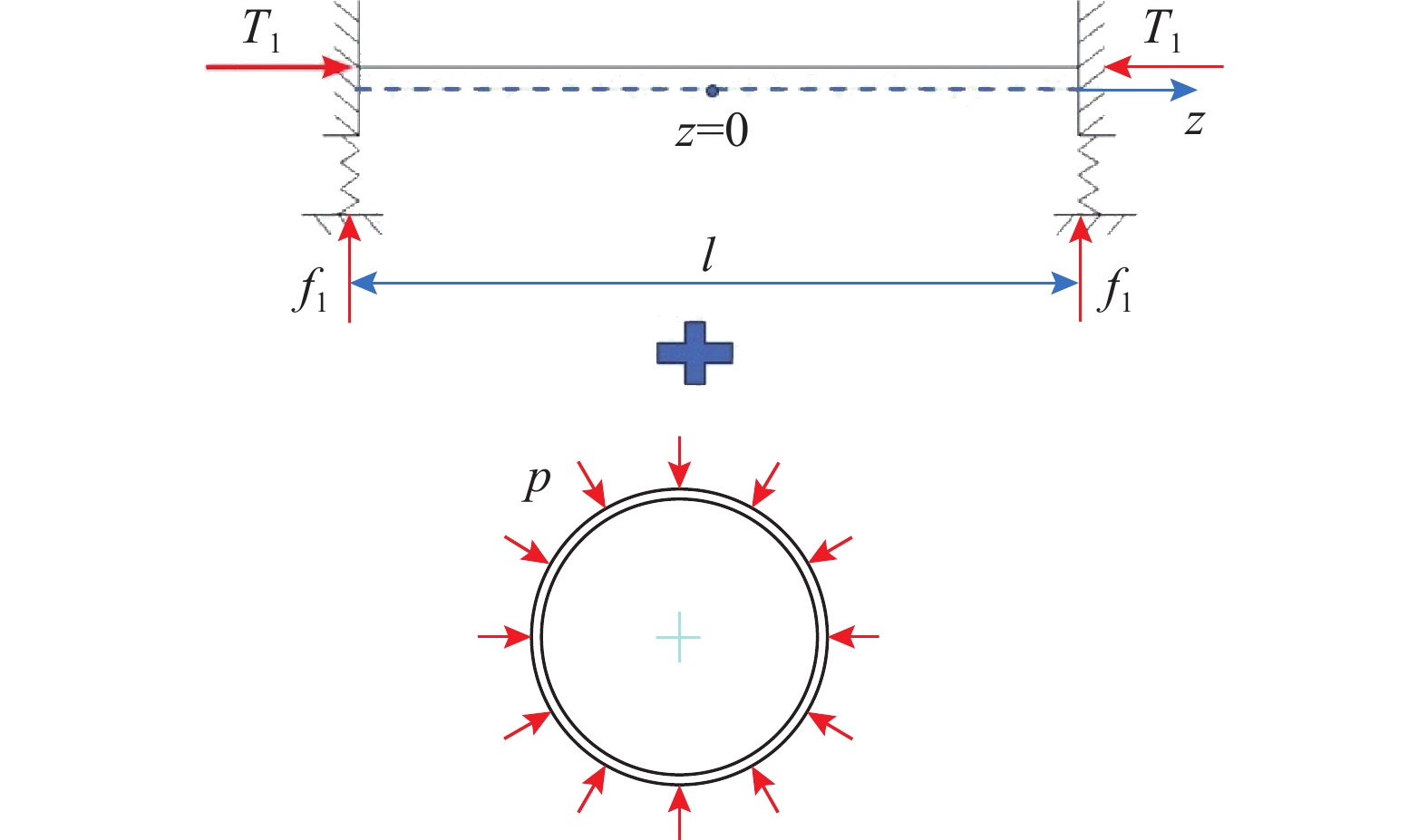
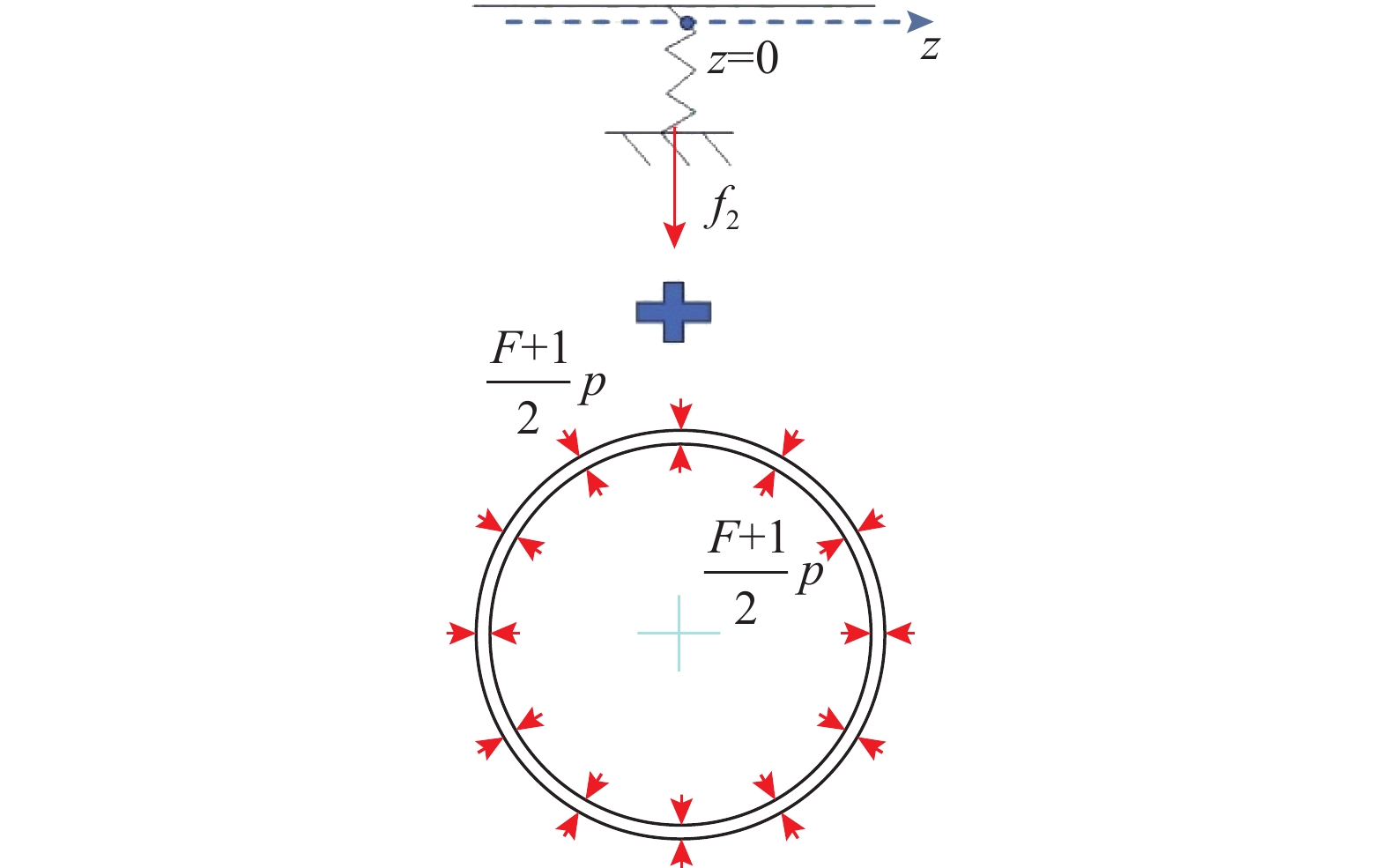
显然，传统圆柱壳力学模型采用的是通过静水压力作用下轴向载荷与径向载荷联立弯曲微分方程^[19]分析的方法。由于环肋圆柱壳由圆柱壳、肋骨腹板、肋骨面板三部分组成，在静水压力作用下，由于载荷是轴对称的，环肋圆柱壳的环壳结构(圆柱壳、肋骨面板)变形也是轴对称的，不防将静水压力作用下的环壳简化为轴向力作用下弯曲梁与径向载荷下平面应变圆环的叠加，其中圆柱壳为闭合环壳，如图3所示；肋骨面板为非闭合环壳，如图4所示；圆柱壳与肋骨腹板之间的相互作用力为${f_1}$，肋骨腹板与肋骨面板之间的相互作用力为${f_2}$时，即肋骨腹板此时可视为内、外表面分别承受径向载荷${f_1}$、${f_2}$的平面应变圆环，如图5所示。

图  3  圆柱壳力学模型

Figure  3.  Mechanical model of cylindrical shell

下载: 全尺寸图片 幻灯片

图  4  肋骨面板力学模型

Figure  4.  Mechanical model of rib panel

下载: 全尺寸图片 幻灯片

图  5  肋骨腹板力学模型

Figure  5.  Mechanical model of rib web plate

下载: 全尺寸图片 幻灯片

相比于传统力学模型，将圆柱壳简化为轴向力作用下的弯曲梁和径向力作用下的平面圆环组合力学模型，既避免了将作用于圆柱壳表面的径向载荷笼统地等效作用于中面的问题(当厚径比$t/R$逐渐超出传统薄壳范畴时，这种等效会引起较大误差)，将肋骨腹板化为纯平面圆环问题、圆柱壳和肋骨面板化为部分平面圆环问题，还能有效考虑沿厚度方向的应力分布，进而综合分析环肋圆柱壳结构的三维应力。

2   基于弯曲微分方程的挠度与应力分析

2.1   考虑三向应力的弯曲微分方程

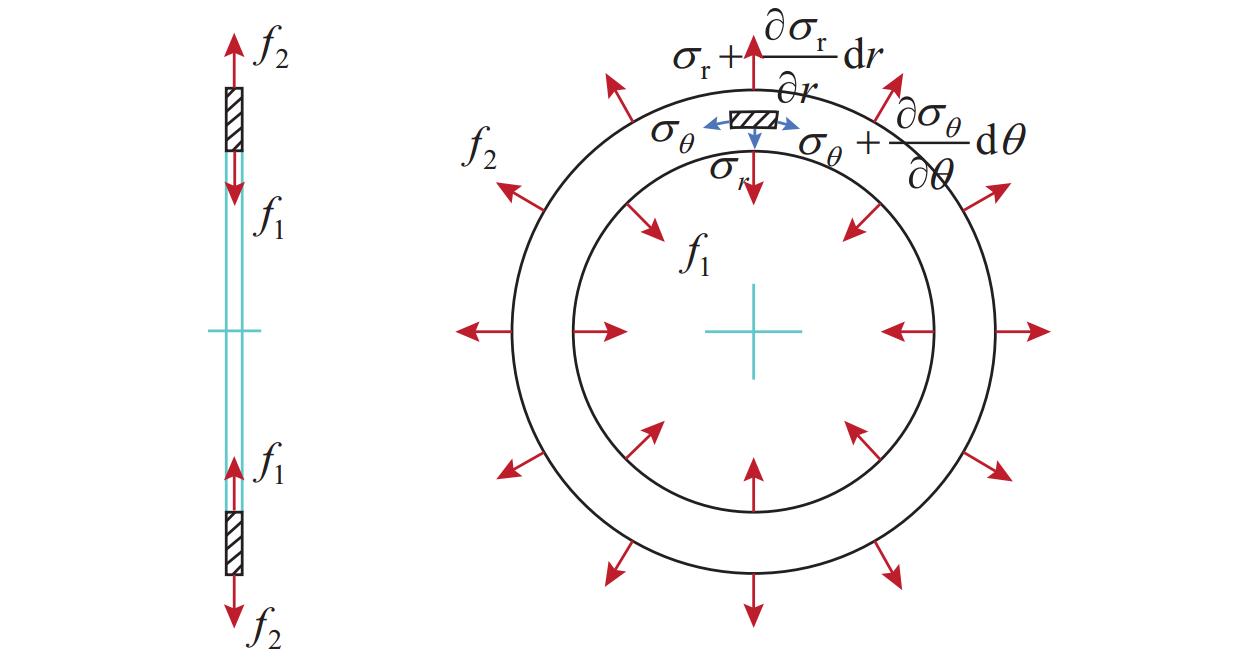
对于图4、图5力学模型中的轴对称等厚环壳，可用两个直径面切出1单位宽度(${\text{d}}s = R{\text{d}}\theta = 1$)的梁带进行研究^[20]，如图6所示。

图  6  轴对称环壳的梁带受力示意图

Figure  6.  Force of an axisymmetric ring shell

下载: 全尺寸图片 幻灯片

当中曲面半径为$R$、厚度为$t$，环壳梁带所受的法向荷重：

该荷重亦形成等效的径向应力$- q$。根据胡克定律，梁带的周向应变：

又因梁带周向线应变$\varepsilon _{\text{2}}^0 = - w/R$($w$为梁带的挠度)，可得出梁带的法向荷重：

从而可得环壳的弯曲微分方程：

式中，$D$为环壳的抗弯刚度。

显然，与传统方法^{[5 − 6]}中的环肋圆柱壳弯曲微分方程$D {w{''''}} - {T _1}{w''} + Et w/{R^{\text{2}}} = \mu {T _1}/R + p$相比，基于三向应力状态的弯曲微分方程式(4)考虑了结构特征$t/R$的影响，同时不考虑径向载荷项$p$(在平面圆环问题中考虑)。

2.2   闭合圆柱壳的弯曲挠度与应力

根据力学模型，闭合圆柱壳的轴向力${T _1} = - 0.5{(1 + 0.5m)^{\text{2}}}pR$，其纵向应力一部分是由轴向力${T _1}$引起的沿厚度不变的部分，另一部分是由梁带弯曲引起的沿厚度变化的部分，因此有：

式中：$r$为柱坐标系下环壳径向方向；${\textit{z}}$为柱坐标系下纵向方向；$w({\textit{z}})$为圆柱壳在轴向力作用下的弯曲挠度；抗弯刚度$D = E {t ^{\text{3}}}/\left[ {{\text{12(1}} - {\mu ^{\text{2}}})} \right]$；厚度特征参数$m = t/R$；轴向力特征参数${\lambda _1} = {{\text{(1}} + 0.5m)^{\text{2}}}R/2$。

根据2.1节方法，圆柱壳的弯曲微分方程为：

该微分方程的通解为：

式中：$\alpha = \sqrt[{\text{4}}]{{{\text{3(1}} - {\mu ^{\text{2}}})}}/\sqrt {Rt}$；$\gamma = {\lambda _1}pR\sqrt {{\text{3(1}} - {\mu ^{\text{2}}})} /(E{t ^{\text{2}}})$；${\alpha _1} = \alpha \sqrt {{\text{1/}}\sqrt {1 + \mu m } - \gamma }$；${\alpha _{\text{2}}} = \alpha \sqrt {{\text{1/}}\sqrt {1 + \mu m } + \gamma }$；${{\text{C}}_1}$、${{\text{C}}_{\text{2}}}$、${{\text{C}}_{\text{3}}}$、${{\text{C}}_{\text{4}}}$为待定常数。因${\textit{z}} = 0$设置在肋骨之间的跨中，圆柱壳挠度对称于坐标轴，即有${{\text{C}}_{\text{2}}} = {{\text{C}}_{\text{3}}} = 0$。另有边界条件：① 肋骨处的转角为0，即${w'}({\textit{z}} = l/2) = 0$；② 肋骨处的壳板剪力大小是肋骨腹板作用力的1/2，即${\text{2}}D{w'''}({\textit{z}} = 0) = {f_1}$。由此，可以求出：

式中：

因此，可以得出轴向力${T _1}$作用下圆柱壳梁带的弯曲挠度为：

以及相应的纵向应力：

式中：${Q_{\text{3}}} = {Q_1}({\alpha _1^2} - {\alpha _2^2}) + {\text{2}}{Q_2}{\alpha _1}{\alpha _{\text{2}}}$；${Q_{\text{4}}} = {Q_2}({\alpha _1^2} - {\alpha _2^2}) - {\text{2}}{Q_1}{\alpha _1}{\alpha _{\text{2}}}$。

根据弯曲挠度$w({\textit{z}})$和纵向应力${\sigma _{\textit{z}}}(r,{\textit{z}})$，可进一步得出圆柱壳梁带弯曲对应的径向应力${\sigma _{r1}}(r,{\textit{z}})$和周向应力${\sigma _{\theta 1}}(r,{\textit{z}})$为：

2.3   肋骨面板的弯曲挠度与应力

根据力学模型，非闭合环壳肋骨面板轴向力${T _1} = - 0.5(F + {\text{1)}}p{t _{\text{f}}}$，梁带纵向应力一部分是水压力$- 0.5(F + {\text{1)}}p$(外肋骨时为$- p$、内肋骨时为0)，另一部分是梁带弯曲引起，即：

式中：$w_{\text{f}}({\textit{z}})$为面板挠度；抗弯刚度${D _{\text{f}}} = E t _{\text{f}}^{\text{3}}/\left[ {{\text{12(1}} - {\mu ^{\text{2}}})} \right]$；面板环壳轴向力特征参数${\lambda _{\text{2}}} = 0.5(F + {\text{1)}}{t _{\text{f}}}$。

根据2.1节方法，肋骨面板的弯曲微分方程为：

式中，肋骨面板的厚度特征参数$k = {t _{\text{f}}}/{R_{\text{f}}}$，该微分方程的通解为：

式中：$\beta = \sqrt[{\text{4}}]{{{\text{3(1}} - {\mu ^{\text{2}}})}}/\sqrt {{R_{\text{f}}}{t _{\text{f}}}}$；$\kappa = {\lambda _{\text{2}}}p{R_{\text{f}}}\sqrt {{\text{3(1}} - {\mu ^{\text{2}}})} {{/E}}$；${\beta _1} = \beta \sqrt {{\text{1/}}\sqrt {1 + \mu k} - \kappa }$；${\beta _{\text{2}}} = \beta \sqrt {{\text{1/}}\sqrt {1 + \mu k} + \kappa }$；${{\text{G}}_1}$、${{\text{G}}_{\text{2}}}$、${{\text{G}}_{\text{3}}}$、${{\text{G}}_{\text{4}}}$为待定常数。显然，当为内肋骨或忽略非闭合环壳的轴向力时，有${\beta _1} = {\beta _{\text{2}}} = \beta /\sqrt[{\text{4}}]{{1 + \mu k}}$。

因${\textit{z}} = 0$设置在肋骨位置，此时有边界条件：① 肋骨处的转角为0，即$w_{\text{f}}'({\textit{z}} = 0) = 0$；② 肋骨处的壳板剪力大小是肋骨腹板作用力的1/2，即${\text{2}}{D _{\text{f}}}w_{\text{f}}'''({\textit{z}} = 0) = {f_2}$；③ 面板边缘处于自由状态，其弯矩和剪力为0，即$w_{\text{f}}''({\textit{z}} = W/2) = 0$，$w_{\text{f}}'''({\textit{z}} = W/2) = 0$。由此可以求出：

式中：

因此，可以得出肋骨面板梁带的弯曲挠度为：

以及相应的纵向应力：

式中：${Q_{\text{9}}} = {Q_{\text{5}}}({\beta _1^2} - {\beta _2^2}) + {\text{2}}{Q_{\text{8}}}{\beta _1}{\beta _{\text{2}}}$；${Q_{{\text{10}}}} = {Q_{\text{6}}}({\beta _1^2} - {\beta _2^2}) - 2{Q_{\text{7}}}{\beta _1}{\beta _{\text{2}}}$；${Q_{{\text{11}}}} = {Q_{\text{7}}}({\beta _1^2} - {\beta _2^2}) + {\text{2}}{Q_{\text{6}}}{\beta _1}{\beta _{\text{2}}}$；${Q_{{\text{12}}}} = {Q_{\text{8}}}({\beta _1^2} - {\beta _2^2}) - 2{Q_{\text{5}}}{\beta _1}{\beta _{\text{2}}}$。

根据弯曲挠度$w_{\text{f}}({\textit{z}})$和纵向应力${\sigma _{{\textit{z}}M}}(r,{\textit{z}})$，可进一步得出肋骨面板梁带弯曲对应的径向应力${\sigma _{rM1}}(r,{\textit{z}})$和周向应力${\sigma _{\theta M1}}(r,{\textit{z}})$为：

3   基于平面应变圆环的径向变形和应力分析

3.1   轴对称平面应变问题分析方法

根据弹性力学平面问题分析方法，轴对称平面圆环的径向变形可表达为^{[21 − 22]}：

式中：${u _r }(r)$为径向变形；${\text{A}}$、${\text{C}}$为与内外作用载荷相关的待定常数。根据几何方程和胡克定律，可得平面圆环的径向应力${\sigma _{\theta}}(r)$和周向应力${\sigma _{\theta}}(r)$为：

式中：$r$为柱坐标系下的环壳径向方向；$\theta$为柱坐标系下的环壳周向方向。

3.2   圆柱壳的径向变形与应力

根据3.1节方法，圆柱壳平面圆环的径向应力满足边界条件：${\sigma _{r2}}(R + 0{{.5t)}} = - p$、${\sigma _{r2}}(R - 0{{.5t)}} = 0$，由此可以求出圆柱壳圆环的径向变形${u _{r2}}(r)$和平面径向应力${\sigma _{r2}}(r)$、周向应力${\sigma _{\theta 2}}(r)$分别为：

式中：${Q_{{\text{13}}}} = {{\text{(1}} + 0.5m)^{\text{2}}}/(2m)$；${Q_{{\text{14}}}} = {{\text{(1}} - 0.5m)^{\text{2}}}/(2m)$。

3.3   肋骨腹板的径向变形与应力

根据3.1节方法，肋骨腹板平面圆环的径向应力满足边界条件：${\sigma _{rF1}}({R_{\text{h}}} - 0.5FH) = - (F + 1)p/2 + F{f_1}/\delta$、${\sigma _{rF1}}({R_{\text{h}}} + 0.5FH) = - (F + 1)p/2 + F{f_2}/\delta$，由此可以求出肋骨腹板圆环的径向变形${u _{rF1}}(r)$和平面径向应力${\sigma _{rF1}}(r)$、周向应力${\sigma _{\theta F1}}(r)$分别为：

式中：${Q_{{\text{15}}}} = {\left( {1 + 0.5nF} \right)^2}/(2n)$；${Q_{{\text{16}}}} = {\left( {1 - 0.5nF} \right)^2}/(2n)$。

3.4   肋骨面板的径向变形与应力

根据3.1节方法，肋骨面板平面圆环的径向应力满足边界条件：${\sigma _{rM2}}({R_{{\text{fo}}}}) = - 0{\text{.5}}\left( {F + 1} \right)p$、${\sigma _{rM2}}({R_{{\text{fi}}}}) = - 0{\text{.5}}\left( {F + 1} \right)p$，由此可以求出肋骨面板圆环的径向变形${u _{rM2}}(r)$和平面径向应力${\sigma _{rM2}}(r)$、周向应力${\sigma _{\theta M2}}(r)$分别为：

4   环肋圆柱壳的三维应力表征方法

4.1   圆柱壳的三维应力表达式

圆柱壳的纵向应力为${\sigma _{\textit{z}}}(r,{\textit{z}})$，将闭合圆柱壳弯曲问题和平面应变圆环问题的推导结果叠加，根据式(9)、式(11)和式(21)，可以得出圆柱壳的组合径向变形${u _r }(r,{\textit{z}})$为：

以及圆柱壳的组合径向应力${\sigma _r }(r,{\textit{z}})$和周向应力${\sigma _{\theta}}(r,{\textit{z}})$分别为：

4.2   肋骨腹板的三维应力表达式

显然，肋骨腹板的纵向应力为${\sigma _{{\textit{z}}F}}(r) = - 0{\text{.5}}( F + 1 )p$(外肋骨时为$- p$、内肋骨时为0)。结合3.3节结果，肋骨腹板的径向变形为：

考虑纵向载荷对肋骨腹板平面圆环的横向效应，根据平面应变以$\mu /(1 - \mu )$叠加纵向应力${\sigma _{{\textit{z}}F}}(r)$的影响，可得肋骨腹板的径向应力${\sigma _{rF}}(r)$、周向应力${\sigma _{\theta F}}(r)$分别为：

4.3   肋骨面板的三维应力表达式

肋骨面板的纵向应力为${\sigma _{{\textit{z}}M}}(r,{\textit{z}})$，将肋骨面板弯曲问题和平面应变圆环问题的推导结果叠加，根据式(16)、式(18)和式(23)，可以得出肋骨面板的组合径向变形${u _{rM}}(r)$为：

以及肋骨面板的组合径向应力${\sigma _{rM}}(r,{\textit{z}})$和周向应力${\sigma _{\theta M}}(r,{\textit{z}})$分别为：

4.4   作用力参数的联立求解

在上述环肋圆柱壳三维应力表征方法中，包含两个作用力未知参数${f_1}$、${f_2}$。作为完整结构，圆柱壳与肋骨腹板连接处、肋骨腹板与面板连接处的变形是连续一致的，即有变形边界条件：

据此两个方程，可求出两未知参数${f_1}$、${f_2}$分别为：

式中：

5   环肋圆柱壳算例计算分析

采用本文方法对具有大深度($p$=90 MPa)、大厚度($t/R$>0.05)、矮宽型肋骨(W/H>1.0)等结构设计特征的环肋圆柱壳(表1)开展应用计算，并与有限元仿真方法、传统应力分析方法的计算结果进行比较分析，计算时材料弹性模量取115 GPa，泊松比取0.34。

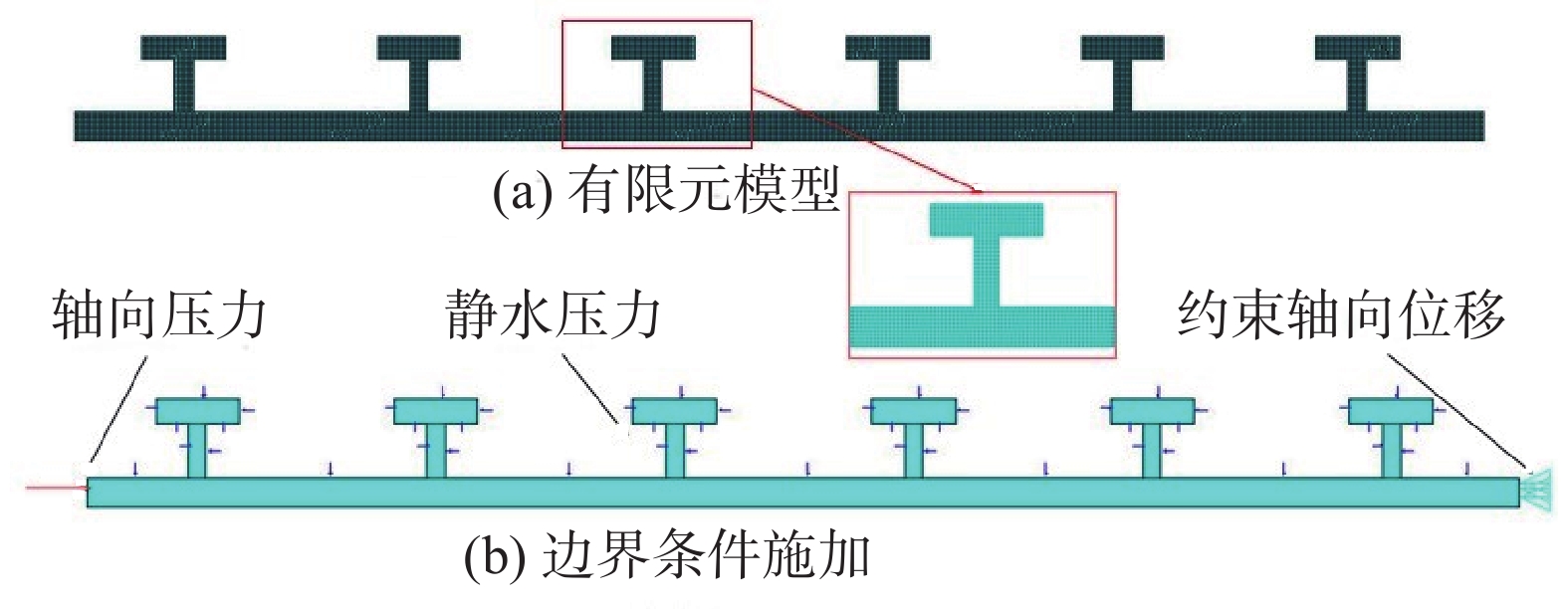
表  1  环肋圆柱壳算例参数表

Table  1.  Calculation example of ring-stiffened cylindrical shell

参数名称	参数/mm
圆柱壳内半径${R_{\text{i}}}$	500
圆柱壳厚度$t$	50
肋骨腹板高度$H$	90
肋骨腹板厚度$\delta$	30
肋骨面板宽度$W$	140
肋骨面板厚度${t _{\text{f}}}$	40
相邻肋骨间距$l$	400
肋骨布置系数$F$	1

下载: 导出CSV 

| 显示表格

选用2维实体单元^[23]建立轴对称有限元模型，按t/N进行单元网格划分(即网格尺寸为圆柱壳厚度的N等分)，在模型外表面(包括壳板和肋骨)施加均布线载荷$p$(模拟静水压力)，在模型一端施加均布线载荷$p{({R_{\text{i}}} + {{t)}}^{\text{2}}}/{\text{(2}}{R_{\text{i}}}t + {t ^2})$(模拟闭合圆柱壳的轴向力)，模型另一端施加轴向位移约束(模拟约束刚体位移)，如图7所示。

图  7  环肋圆柱壳的有限元模型

Figure  7.  Finite element model of ring-stiffened cylindrical shell

下载: 全尺寸图片 幻灯片

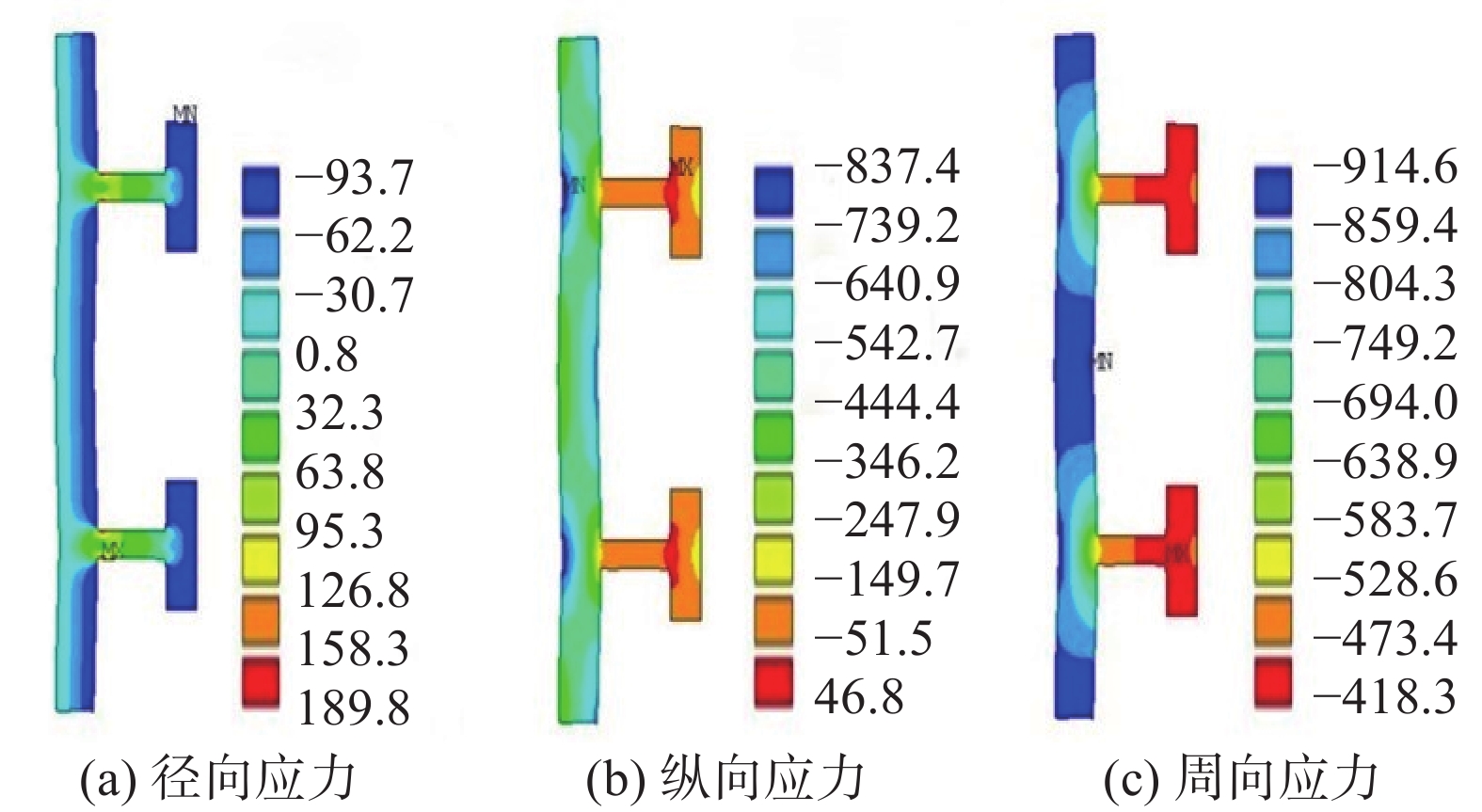
环肋圆柱壳的应力仿真云图如图8所示，在大深度静水压力作用下，环肋圆柱壳的壳板最大纵向应力位于肋骨跨端位置、壳板最大周向应力位于跨中位置、肋骨最大周向应力位于肋骨腹板下缘位置。

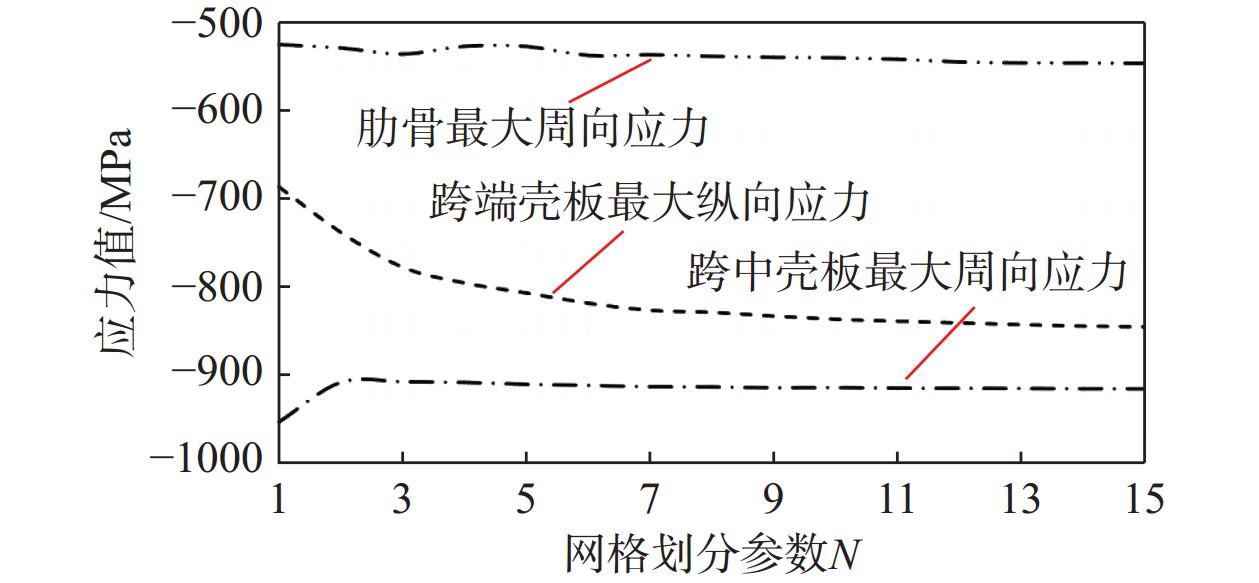
为观察单元网格尺寸对环肋圆柱壳典型应力计算结果的影响，按不同的网格划分参数N进行系列计算。显然，N取15时环肋圆柱壳的应力仿真计算结果是趋于稳定的，如图9所示，本文将提取该网格尺寸下的有限元仿真应力结果进行比较。

图  8  环肋圆柱壳的应力仿真云图　/MPa

Figure  8.  Stress cloud map of ring-stiffened cylindrical shell

下载: 全尺寸图片 幻灯片

图  9  单元网格尺寸对环肋圆柱壳应力仿真计算结果的影响

Figure  9.  The influence of element size on the stress of ring-stiffened cylindrical shell

下载: 全尺寸图片 幻灯片

环肋圆柱壳典型应力的三维应力分析方法和有限元仿真计算结果列于表2。结果表明：① 关于圆柱壳壳板应力，不论是肋骨跨中或是肋骨根部，三维应力分析方法计算结果与有限元仿真结果吻合很好，且偏安全；② 关于肋骨腹板应力，两者计算结果也较为吻合；③ 关于肋骨面板应力，其纵向应力和周向应力的解析计算结果偏大、径向应力的解析计算结果偏小，表明三维应力分析方法中非闭合环壳采用中面弯曲力学模型整体而言是略偏保守的。

表  2  三维应力分析方法和有限元仿真结果比较

Table  2.  The stresses results of three dimensional stress analysis method and finite element simulation

典型应力名称			本文方法 计算值/MPa	有限元 仿真值/MPa
肋骨跨中壳板	纵向应力	外表面	−697.8	−679.4
	径向应力	外表面	−98.2	−85.5
	周向应力	外表面	−921.6	−913.0
		内表面	−889.8	−887.6
		中 面	−905.7	−899.1
肋骨根部壳板	纵向应力	内表面	−915.7	−846.0
	周向应力	外表面	−603.9	−584.5
		内表面	−964.0	−906.3
		中 面	−784.0	−745.4
肋骨腹板	纵向应力	形心处	−90.0	−89.9
	径向应力	形心处	57.2	55.7
	周向应力	上缘	−477.2	−436.4
		下缘	−556.5	−546.6
肋骨面板外表面	纵向应力	中心	−330.5	−212.9
		边缘	−90.0	−90.2
	径向应力	中心	−66.5	−86.1
		边缘	−67.5	−89.5
	周向应力	中心	−550.1	−490.0
		边缘	−461.9	−431.4

下载: 导出CSV 

| 显示表格

两者方法结果均显示肋骨面板的中心和边缘应力存在明显差异，证明将肋骨面板假设为一维圆环结构是显然不合理的；另外还发现肋骨根部壳板内表面纵向应力(−915.7 MPa)小于其周向应力(−964.0 MPa)，以及肋骨面板周向应力(−550.1 MPa)大于肋骨腹板上缘周向应力(−477.2 MPa)的情况，表现出与传统薄环肋圆柱壳显著不同的应力特性。

针对环肋圆柱壳结构的关键应力(规范标准中的强度校核应力项)，将前述计算结果进一步与采用朱邦俊等^[13]提出的应力分析方法的计算结果进行比较(表3)。结果显示，本文提出的三维应力分析方法计算结果与有限元仿真计算结果相对而言更为吻合；文献方法关于跨中壳板周向应力和肋骨周向应力的计算值分别偏低约6.9%、12.1%，而关于肋骨根部壳板纵向应力的计算值则偏大约10.7%，说明文献方法等传统应力分析方法用于大深度、大厚度、矮宽型肋骨等结构设计特征的环肋圆柱壳结构设计的计算结果是偏危险的。

表  3  环肋圆柱壳关键应力项的结果比较

Table  3.  The key stresses of ring-stiffened cylindrical shell /MPa

关键应力名称	本文方法 计算值	文献[13] 方法计算值	有限元 仿真值
肋骨跨中壳板中面周向应力	−905.7	−840.6	−899.1
肋骨根部壳板内表面纵向应力	−915.7	−947.2	−846.0
肋骨最大周向应力	−556.5	−487.6	−546.6

下载: 导出CSV 

| 显示表格

为观察本文提出的三维应力分析方法用于一般深度耐压结构应力计算的情况，对某一T形环肋圆柱壳^[24](计算压力15 MPa、结构特征t/R=0.028)开展计算，并与文中给出的计算值和试验值进行比较。圆柱壳内半径500 mm、壳板厚度14 mm，相邻肋骨间距400 mm，肋骨面板宽度50 mm、厚度12 mm，腹板高度90 mm、厚度10 mm，材料弹性模量取196 GPa、泊松比取0.3。

表4应力结果表明，本文方法关于环肋圆柱壳典型应力的计算值与文献中的应力结果基本一致，且与试验结果更为吻合，进一步显示了三维应力分析方法的正确可靠性。其中肋骨根部应力计算值高于试验值是因为肋骨根部应力集中，采用应变片测量方法一般较难测得其峰值所致。

表  4  计算值与试验值比较

Table  4.  Comparison between calculated values and experimental values

应力名称	本文方法 计算值/MPa	文献[24] 计算值/MPa	文献[24] 试验值/MPa
肋骨跨中壳板中面周向应力	571.1	−556.8	−565.2
肋骨根部壳板内表面纵向应力	−610.6	−615.9	−559.3
肋骨面板周向应力	−225.6	−243.3	−221.6

下载: 导出CSV 

| 显示表格

6   结论

本文围绕环肋圆柱壳结构开展三维应力分析方法研究，主要工作和结论如下：

(1)将环肋圆柱壳的圆柱壳、肋骨面板分别视为闭合环壳和非闭合环壳结构，肋骨腹板视为平面圆环结构，提出了一种新的环肋圆柱壳简化力学模型，使静水压力作用下的环肋圆柱壳应力分析转化为轴向力作用下的复杂弯曲梁问题和径向力作用下的轴对称平面问题的叠加组合。

(2)提出考虑三维应力状态的环壳弯曲微分方程，并结合轴对称平面问题分析方法，推导给出了环肋圆柱壳的三维应力计算式，可用于计算分析环肋圆柱壳任意位置的三维应力。

(3)以某具有大深度、大厚度、矮宽型肋骨等结构设计特征的环肋圆柱壳进行算例分析，结果表明，本文提出的三维应力分析方法不仅具有较好的计算精度，且计算结果是偏安全的。

(4)算例结果表明，不仅肋骨面板的中心和边缘应力存在明显差异，且对于新结构设计特征的环肋圆柱壳，其肋骨根部壳板应力与肋骨应力还表现出与传统薄环肋圆柱壳显著不同的应力特性。