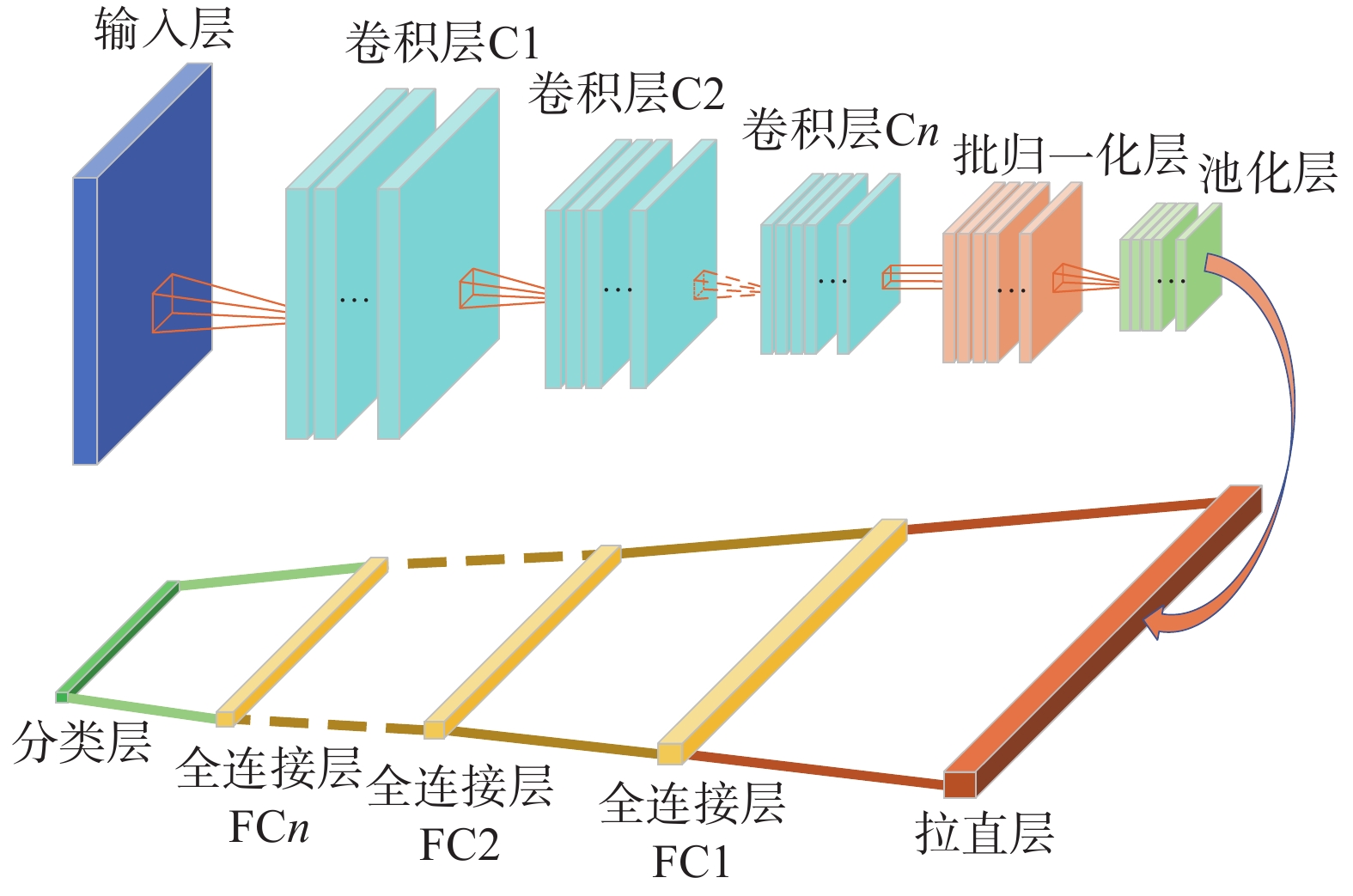
STRUCTURAL HEALTH MONITORING BASED ON INNER PRODUCT MATRIX AND DEEP LEARNING
-
摘要: 环境激励下仅利用振动响应的结构健康监测方法，因其便于实现在线监测受到了越来越多的关注。该文回顾了以振动时域响应相关性分析为基础的结构特征参数(即内积向量)的基本概念及特征。为了从已有测试数据中提取更多的结构特征参数，分别以各个响应测点为参考点来构建多个内积向量并组成矩阵，将内积向量扩展到了内积矩阵。进而以内积矩阵为结构特征参数，结合深度卷积神经网络的特征提取能力，提出了基于内积矩阵及深度学习的结构健康监测方法。典型航空加筋壁板螺栓松动监测的实验研究结果表明，仅利用结构在环境激励下部分测点的振动时域响应，该文方法可以准确地识别螺栓松动位置。Abstract: Structural health monitoring methods using vibration responses only under ambient excitation are appealing as its convenience to realize on-line monitoring. The basic concepts and characteristics of structural characteristic parameter (i.e. inner product vector) based on the correlation analysis of time domain vibration response are reviewed. In order to extract more structural characteristic parameters from the existing test data, the inner product vector is extended to the inner product matrix by using several inner product vectors which are constructed by setting each measurement point as the reference measurement point. Furthermore, taking the inner product matrix as the structural characteristic parameter and combining the feature extraction ability of deep convolution neural network, a structural health monitoring method based on deep learning and inner product matrix is proposed. The experimental results of monitoring the bolt loosening of a typical aeronautical stiffened panel show that the bolt loosening position can be correctly located using the time domain vibration response only under ambient excitation.
-
-
![]()
图 1 结构健康监测标签数据库的构建
Figure 1. Construction of the labelled database for structural health monitoring
![]()
图 2 深度卷积神经网络结构示意图
Figure 2. Schematic diagram of the deep convolutional neural network architecture
表 1 采用的网络结构
Table 1 The utilized network architecture
层 类型 输入维数 输出维数 核数量 核尺寸 步长 填补 激活函数 1 Convolution (15,15,1) (15,15,16) 16 (3,3) 1 Same ReLU 2 Convolution (15,15,16) (15,15,32) 32 (3,3) 1 Same ReLU 3 Batch Normalization (15,15,32) (15,15,32) / / / / / 4 Max Pooling (15,15,32) (7,7,32) / (2,2) 2 / / 5 Flatten (7,7,32) (1568) / / / / / 6 Fully Connected (1568) (32) / / / / / 7 Softmax (32) (7) / / / / / 
下载: 导出CSV
表 2 不同数据容量下网络的损失函数值及识别准确率
Table 2 The loss value and accuracy for different datasets
数据容量/个 64 128 256 512 1024 损失函数值 1.4027 1.0008 0.5805 0.2911 0.1977 准确率 训练集 0.4665 0.6746 0.8283 0.9480 0.9745 验证集 0.4444 0.6556 0.8389 0.9471 0.9735 测试集 0.4000 0.6222 0.8324 0.9413 0.9735 固定测试集准确率 0.4657 0.7129 0.8243 0.9514 0.9742
下载: 导出CSV
表 3 15个测点下网络的损失函数值及识别准确率
Table 3 The loss value and accuracy of the network by 15 measurement points
计算内积矩阵的
加速度采样点数/个512 1024 2048 4096 8192 损失函数值 0.1977 0.1437 0.0762 0.0508 0.0535 准确率 训练集 0.9745 0.9829 0.9956 0.9976 0.9976 验证集 0.9735 0.9847 0.9930 0.9958 0.9972 测试集 0.9735 0.9847 0.9958 0.9972 0.9972
下载: 导出CSV
表 4 8个测点下网络的损失函数值及识别准确率
Table 4 The loss value and accuracy of the network by 8 measurement points
计算内积矩阵的
加速度采样点数/个512 1024 2048 4096 8192 损失函数值 0.4155 0.2571 0.1574 0.1064 0.0741 准确率 训练集 0.8849 0.9452 0.9775 0.9908 0.9969 验证集 0.8703 0.9386 0.9665 0.9847 0.9986 测试集 0.8954 0.9456 0.9721 0.9861 0.9944
下载: 导出CSV
表 5 4个测点下网络的损失函数值及识别准确率
Table 5 The loss value and accuracy of the network by 4 measurement points
计算内积矩阵的
加速度采样点数/个512 1024 2048 4096 8192 损失函数值 0.7573 0.5631 0.3765 0.2136 0.1444 准确率 训练集 0.7573 0.8214 0.8851 0.9480 0.9817 验证集 0.7406 0.8257 0.8884 0.9568 0.9833 测试集 0.7838 0.8257 0.8842 0.9568 0.9847
下载: 导出CSV
表 6 不同情况下的计算耗时
Table 6 Computational time consuming for different cases
计算内积矩阵的
加速度采样点数/个512 1024 2048 4096 8192 15测点 构建数据库 4.706 5.830 8.520 14.228 23.823 模型训练 68.306 55.073 52.737 38.108 37.577 8测点 构建数据库 2.113 2.764 2.798 2.978 3.471 模型训练 73.251 61.583 59.066 45.437 42.589 4测点 构建数据库 1.186 1.509 1.556 1.624 1.642 模型训练 73.536 69.565 69.918 47.164 45.935 注：计算耗时单位为秒，采用的计算机为：CPU，Intel(R) Xeon(R) E-2236 3.4 GHz；内存，32 GB；显卡，NVIDIA Quadro P1000 4 GB。
下载: 导出CSV
表 7 采用远离螺栓松动位置的4个测点时网络的损失函数值及识别准确率
Table 7 The loss value and accuracy of the network by 4 measurement points located far from the loosed bolt
计算内积矩阵的
加速度采样点数/个512 1024 2048 4096 8192 损失函数值 0.7200 0.6203 0.3606 0.2042 0.1533 准确率 训练集 0.7663 0.8308 0.9074 0.9660 0.9796 验证集 0.7406 0.8285 0.9010 0.9707 0.9763 测试集 0.7824 0.8187 0.8968 0.9540 0.9846
下载: 导出CSV
-
[1] Yang Z C, Wang L, Wang H, et al. Damage detection in composite structures using vibration response under stochastic excitation [J]. Journal of Sound and Vibration, 2009, 325(4/5): 755 − 768. doi: 10.1016/j.jsv.2009.03.040
[2] 翁顺, 朱宏平. 基于有限元模型修正的土木结构损伤识别方法[J]. 工程力学, 2021, 38(3): 1 − 16. doi: 10.6052/j.issn.1000-4750.2020.06.ST02 Weng Shun, Zhu Hongping. Damage identification of civil structures based on finite element model updating [J]. Engineering Mechanics, 2021, 38(3): 1 − 16. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.06.ST02
[3] 侯博文, 李佳静, 高亮, 等. 基于脉冲激励下钢轨振动响应的扣件失效识别方法[J]. 工程力学, 2021, 38(2): 122 − 133. doi: 10.6052/j.issn.1000-4750.2020.04.0210 Hou Bowen, Li Jiajing, Gao Liang, et al. Failure identification method of fastening system based on rail response under pulse excitation [J]. Engineering Mechanics, 2021, 38(2): 122 − 133. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.04.0210
[4] Bull L A, Worden K, Dervilis N. Towards semi-supervised and probabilistic classification in structural health monitoring [J]. Mechanical Systems and Signal Processing, 2020, 140: 106653. doi: 10.1016/j.ymssp.2020.106653
[5] Sarmadi H, Karamodin A. A novel anomaly detection method based on adaptive Mahalanobis-squared distance and one-class kNN rule for structural health monitoring under environmental effects [J]. Mechanical Systems and Signal Processing, 2020, 140: 106495. doi: 10.1016/j.ymssp.2019.106495
[6] 李惠, 鲍跃全, 李顺龙, 等. 结构健康监测数据科学与工程[J]. 工程力学, 2015, 32(8): 1 − 7. doi: 10.6052/j.issn.1000-4750.2014.08.ST11 Li Hui, Bao Yuequan, Li Shunlong, et al. Data science and engineering for structural health monitoring [J]. Engineering Mechanics, 2015, 32(8): 1 − 7. (in Chinese) doi: 10.6052/j.issn.1000-4750.2014.08.ST11
[7] Bao Y Q, Chen Z C, Wei S Y, et al. The state of the art of data science and engineering in structural health monitoring [J]. Engineering, 2019, 5(2): 234 − 242. doi: 10.1016/j.eng.2018.11.027
[8] Goodfellow I, Bengio Y, Courville A. Deep learning [M]. USA: The MIT Press, 2016.
[9] 丁建立, 邹云开, 王静, 等. 基于深度学习的ADS-B异常数据检测模型[J]. 航空学报, 2019, 40(12): 323220. Ding Jianli, Zou Yunkai, Wang Jing, et al. ADS-B anomaly data detection model based on deep learning [J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(12): 323220. (in Chinese)
[10] 陈海昕, 邓凯文, 李润泽. 机器学习技术在气动优化中的应用[J]. 航空学报, 2019, 40(1): 522480. Chen Haixin, Deng Kaiwen, Li Runze. Utilization of machine learning technology in aerodynamic optimization [J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(1): 522480. (in Chinese)
[11] Zhao R, Yan R Q, Chen Z H, et al. Deep learning and its applications to machine health monitoring [J]. Mechanical Systems and Signal Processing, 2019, 115(1): 213 − 237.
[12] 杨娜, 张翀, 李天昊. 基于无人机与计算机视觉的中国古建筑木结构裂缝监测系统设计[J]. 工程力学, 2021, 38(3): 27 − 39. doi: 10.6052/j.issn.1000-4750.2020.04.0263 Yang Na, Zhang Chong, Li Tianhao. Design of crack monitoring system for Chinese ancient wooden buildings based on UAV and CV [J]. Engineering Mechanics, 2021, 38(3): 27 − 39. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.04.0263
[13] Cha Y J, Choi W, Büyüköztürk O. Deep learning - based crack damage detection using convolutional neural networks [J]. Computer - Aided Civil and Infrastructure Engineering, 2017, 32(5): 361 − 378. doi: 10.1111/mice.12263
[14] Dorafshan S, Thomas R J, Maguire M. Comparison of deep convolutional neural networks and edge detectors for image-based crack detection in concrete [J]. Construction and Building Materials, 2018, 186(1): 1031 − 1045.
[15] Liu H, Zhang Y F. Image-driven structural steel damage condition assessment method using deep learning algorithm [J]. Measurement, 2019, 133(1): 168 − 181.
[16] Reddy A, Indragandhi V, Ravi L, et al. Detection of cracks and damage in wind turbine blades using artificial intelligence-based image analytics [J]. Measurement, 2019, 147(1): 106823.
[17] Yao Y, Yang Y, Wang Y P, et al. Artificial intelligence-based hull structural plate corrosion damage detection and recognition using convolutional neural network [J]. Applied Ocean Research, 2019, 90(1): 101823.
[18] Ren Y P, Huang J S, Hong Z Y, et al. Image-based concrete crack detection in tunnels using deep fully convolutional networks [J]. Construction and Building Materials, 2020, 234(1): 117367.
[19] Guo X J, Chen L, Shen C Q. Hierarchical adaptive deep convolution neural network and its application to bearing fault diagnosis [J]. Measurement, 2016, 93(1): 490 − 502.
[20] Jing L Y, Zhao M, Li P, et al. A convolutional neural network based feature learning and fault diagnosis method for the condition monitoring of gearbox [J]. Measurement, 2017, 111(1): 1 − 10.
[21] Chang Y H, Chen J L, Qu C, et al. Intelligent fault diagnosis of wind turbines via a deep learning network using parallel convolution layers with multi-scale kernels [J]. Renewable Energy, 2020, 153(1): 205 − 213.
[22] Chen L T, Xua G H, Zhang S C, et al. Health indicator construction of machinery based on end-to-end trainable convolution recurrent neural networks [J]. Journal of Manufacturing Systems, 2020, 54: 1 − 11. doi: 10.1016/j.jmsy.2019.11.008
[23] Lin Y Z, Nie Z H, Ma H W. Structural damage detection with automatic feature-extraction through deep learning [J]. Computer-Aided Civil and Infrastructure Engineering, 2017, 32(12): 1025 − 1046. doi: 10.1111/mice.12313
[24] Pathirage C S N, Li J, Li L, et al. Structural damage identification based on autoencoder neural networks and deep learning [J]. Engineering Structures, 2018, 172(1): 13 − 28.
[25] Pathirage C S N, Li J, Li L, et al. Development and application of a deep learning-based sparse autoencoder framework for structural damage identification [J]. Structural Health Monitoring, 2019, 18(1): 103 − 122. doi: 10.1177/1475921718800363
[26] Liu J X, Chen S H, Berges M, et al. Diagnosis algorithms for indirect structural health monitoring of a bridge model via dimensionality reduction [J]. Mechanical Systems and Signal Processing, 2020, 136(1): 106454.
[27] Wang L, Yang Z C, Waters T P. Structural damage detection using cross correlation functions of vibration response [J]. Journal of Sound and Vibration, 2010, 329(24): 5070 − 5086. doi: 10.1016/j.jsv.2010.06.020
[28] Wang L, Yang Z C. Effect of response type and excitation frequency range on the structural damage detection method using correlation functions of vibration responses [J]. Journal of Sound and Vibration, 2013, 332(4): 645 − 653. doi: 10.1016/j.jsv.2012.09.027
[29] 王慧, 王乐, 田润泽. 基于时域响应相关性分析及数据融合的结构损伤检测研究[J]. 工程力学, 2020, 37(9): 30 − 37, 111. doi: 10.6052/j.issn.1000-4750.2019.10.0588 Wang Hui, Wang Le, Tian Runze. Structural damage detection using correlation functions of time domain vibration responses and data fusion [J]. Engineering Mechanics, 2020, 37(9): 30 − 37, 111. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.10.0588
计量
- 文章访问数: 1679
- HTML全文浏览量: 351
- PDF下载量: 302
