梁柱节点连接是钢结构的重要构件，节点断裂是钢结构破坏的主要控制极限状态之一。钢结构断裂问题主要包含脆性断裂和延性断裂，低温环境、高强钢和厚板的使用、焊接连接及热影响区等引起的钢结构脆性断裂问题日趋突出^[1]；但在高温下，钢材延性变好，普通钢母材多表现为延性断裂^[2]，钢材高温延性断裂研究可为节点抗火承载力评估提供数据支撑。特别地，高温下和高温后钢梁受拉会产生悬链线效应，造成节点断裂，从而引发整体结构的连续性倒塌，钢材火灾全过程延性断裂性能是研究钢节点断裂对结构倒塌影响的前提。

对于预测钢材无初始裂纹且大范围屈服下的延性断裂行为，传统断裂力学方法具有一定的局限性，尚缺乏统一的钢结构节点断裂评定方法。常温下，钢材断裂主要取决于其等效塑性断裂应变、应力三轴度、Lode角等参数。国内外学者对常温下钢材断裂行为展开了大量研究，发展了延性断裂机理，建立了较完善的基于断裂力学的工程近似计算方法。RICE和TRACEY^[3]最早提出了基于微观机制的断裂预测模型(Rice-Tracey模型)；KANVINDE和DEIERLEIN^[4-5]提出并发展了微孔扩张模型(VGM)和应力修正临界应变模型(SMCS)，该类方法由于参数简单得到了较为广泛的运用。国内学者胡方鑫等^[6]、周晖等^[7]、王元清等^[8]、施刚和陈玉峰^[9]基于延性断裂机理对梁柱节点、焊缝的断裂行为展开相关研究，探讨了荷载类型、焊缝类型及钢材强度对典型构造断裂性能的影响；LIAO等^[10]、王俊杰和王伟^[11]对基于微观机制断裂预测模型参数进行了校准，并对节点延性断裂进行预测。叶继红和范志鹏^[12]采用基于体胞模型空穴演化机理改进了现有的韧性断裂模型，校核了Q345钢材断裂模型参数。

高温下，钢材材性研究主要针对热工性能(如导热系数、热膨胀系数等)和基本力学性能(如弹性模量、屈服强度、极限强度等)^[13]。国外以欧洲规范EN 1993-1-2: 2005^[14]和美国规范ANSI/AISC 360−2016^[15]为代表，给出了钢材高温下弹性模量、比例极限、屈服强度的折减系数；QUTINEN和MAKELAINEN^[16]对S350、S355、S420钢材进行高温下的稳态和瞬态试验，提出了相应高温力学性能模型。国标《建筑钢结构防火技术规范》(GB 51249−2017)^[17]给出了高温下结构钢和耐火钢的弹性模量和屈服强度折减系数；李国强等^[18]、吕彤光^[19]、蒋首超等^[20]对Q345、Q460、Q690结构钢进行了高温材性试验，研究不同钢材在高温下屈服强度、极限强度、断面伸缩率等性能的变化趋势，并推导计算模型；DU等^[21]对1670 MPa平行钢绞线的高温材性进行了试验研究，建立了高温弹性模量、屈服强度和极限强度的数学模型。

对于钢材高温延性断裂性能的研究仍处于起步阶段。EN 1993-1-2: 2005中规定在不同温度下采用相同的断裂应变(屈服的极限应变为0.15，断裂应变为0.2)，而《建筑钢结构防火技术规范》^[17]对钢材高温断裂性能未作规定；BØRVIK等^[22]发现在高应变率下，温度对钢材应力-应变行为的影响不同；曹文衔和沈祖炎^[23]以欧规EN 1993-1-2: 2005高温材性模型为基础，提出了考虑损伤累计效应的火灾升降温全过程钢结构分析材性模型；CAI等^[24]利用ASTM A992钢的试验数据和有限元分析结果，提出了表征颈缩后真实应力-应变关系的广义函数，用于高温断裂模拟的有限元模型；DU等^[21]试验研究了高温下高强钢绞线包括断裂应变的完整应力-应变曲线，并提出了计算高温断裂应变的数学模型。复杂应力和高温共同作用对断裂应变的影响尚不明确，有必要对复杂应力作用下钢材高温断裂行为进行系统研究。

本文对高应力三轴度下Q355钢材火灾全过程拉伸断裂性能进行试验研究，考虑应力三轴度的影响，设计光滑圆棒和缺口圆棒试件，分别进行升温段、降温段和高温后(即火灾全过程)拉伸断裂试验；通过DIC-3D获取材料的工程应力-应变曲线和真实应力-应变曲线，研究应力三轴度和温升历程对材料基本力学性能和断裂性能的影响；通过电镜扫描试件断口，研究火灾全过程下钢材的微观断口形貌和断裂机制；最后，采用SMCS断裂模型表征钢材高温断裂特性，并结合有限元分析，对不同温度下模型参数进行标定。

1   试验方案

1.1   试件设计和工况

所有Q355钢试件是从同一块钢板上切割获取，钢材各项力学指标均符合《低合金高强度结构钢》(GB/T 1591−2018)^[25]中的技术要求。为了考虑应力三轴度对钢材断裂性能的影响，设计光滑圆棒和缺口圆棒两种试件，分别为光滑圆棒(S)、N6缺口圆棒(N6)和N3缺口圆棒(N3)，如表1所示。其中，光滑圆棒试件是为了获取钢材的本构信息以及应力三轴度为1/3时的断裂应变；缺口圆棒是考虑不同应力三轴度影响，为后续校准断裂模型参数提供试验数据。

表  1  试件设计及参数

Table  1.  Test piece design and parameters

试件类型		试件编号	切口 半径/ mm	切口根部 最小截面 直径/mm	应力 三轴 度	加载速率/ (mm·min−1)
常温	平滑 圆棒	SR	−	12.50	0.333	0.3
	N6缺口 圆棒	N6R	6.250	6.25	0.745	0.3
	N3缺口 圆棒	N3R	3.125	6.25	1.037	0.3
升温段	平滑 圆棒	SH2/SH4/SH6	−	12.50	0.333	0.3
	N6缺口 圆棒	N6H2/N6H4/N6H6	6.250	6.25	0.745	0.3
	N3缺口 圆棒	N3H2/N3H4/N3H6	3.125	6.25	1.037	0.3
降温段	平滑 圆棒	SC4-2/SC6-4/ SC6-2	−	12.50	0.333	0.3
	N6缺口 圆棒	N6C4-2/N6C6-4/ N6C6-2	6.250	6.25	0.745	0.3
	N3缺口 圆棒	N3C4-2/N3C6-4/ N3C6-2	3.125	6.25	1.037	0.3
高温后	平滑 圆棒	SA2/SA4/ SA6/SA8	−	12.50	0.333	0.3
	N6缺口 圆棒	N6A2/N6A4/ N6A6/N6A8	6.250	6.25	0.745	0.3
	N3缺口 圆棒	N3A2/N3A4/ N3A6/N3A8	3.125	6.25	1.037	0.3
注：应力三轴度$\eta =1/3+\mathrm{ln}(1+{a/}2)$。

下载: 导出CSV 

| 显示表格

在拉伸过程中试件的应力三轴度是动态变化的。当光滑圆棒试件发生颈缩时，应力状态会随着拉伸变形发展而发生变化，直至断裂，这与母材在发生拉伸断裂时的应力状态是相似的。对光滑圆棒试件施加缺口的主要目的并不是单纯地研究缺口对断裂的影响，更重要的是为了获得不同的初始应力状态，获得更多高应力三轴度范围内的力学性能参数，以校准断裂模型，完善高应力三轴度内的断裂模型参数。

光滑圆棒和缺口圆棒试件采用相同的几何尺寸，满足《金属材料 拉伸试验 第2部分: 高温试验方法》(GB/T 228.2−2015)^[26]要求，试件总长为140 mm，平直段长度为75 mm，如图1所示。在标距范围内预设两种尺寸的缺口：N6(缺口半径为6.25 mm，应力三轴度为0.745)和N3(缺口半径为3.125 mm，应力三轴度为1.037)，两种缺口试件的根部截面直径同为6.25 mm。

图  1  拉伸试件尺寸 /mm

Figure  1.  Geometry size of tensile test specimens

下载: 全尺寸图片 幻灯片

Q355钢材火灾全过程断裂试验分为升温段(H)、降温段(C)以及高温后(A)三种工况。其中，前两种工况采用恒温加载方法，高温后试验对降温至常温的构件进行加载拉伸试验。将试验过程中试件经历的最高温度定义为峰值温度，拉伸加载时的温度定义为拉伸温度(即目标温度)，试件编号为试件类型编号和温度工况编号的组合，具体工况如表1和图2所示。表1中：S、N6、N3分别代表光滑圆棒、N6缺口圆棒和N3缺口圆棒等试件类型；后面的字母和数字分别代表三种试验工况和对应温度，其中，R、H、C、A分别代表常温、升温段、降温段、高温后试验。例如，N6H4代表N6缺口试件升温到400 ℃下的升温段断裂试验工况；N3C6-4代表N3缺口试件升温至600 ℃后降温到400 ℃的降温段断裂试验工况。本实验共设计11个温度工况。高温后试验的最高温度达800 ℃，而升温段试验最高温度仅为600 ℃，这是受限于不同高温炉的温控限制。如图2所示，升温段以20 ℃/min升至预定温度后恒温20 min再进行加载；降温段以20 ℃/min升至预定温度恒温20 min后再以10 ℃/min进行降温。每个温度工况下对3组不同应力三轴度试件进行试验，每组进行2次重复试验，累计对66个试件进行了断裂性能试验研究。

图  2  火灾全过程试验温度工况

Figure  2.  Temperature conditions in the fire test

下载: 全尺寸图片 幻灯片

1.2   试验设备

1.2.1   加载设备

分别进行火灾升温段、降温段以及高温后拉伸断裂试验。加载设备采用MTS LandMark高温材料试验系统，如图3(a)所示，试验机最大拉力为120 kN；升温段和降温段试验的加热系统采用定制的高温炉(升温范围为50 ℃~600 ℃)，高温炉内试件通过自制的耐高温锚具与MTS加载系统相连，如图3(b)所示；高温后试验的加热系统采用马弗炉(升温范围为50 ℃~800 ℃)。试件的力加载方式采用位移控制，根据《金属材料拉伸试验 第2部分: 高温试验方法》(GB/T 228.2−2015)^[26]，设定加载速率为0.3 mm/min，以确保构件在加载过程中排除动力效应的干扰。

图  3  试验装置

Figure  3.  Test setup

下载: 全尺寸图片 幻灯片

1.2.2   测量设备

采用数字图像相关测量系统(DIC-3D)测量构件的应变，如图4所示。通过在试件表面喷涂散斑，获取像素级的位移信息，从而获取试件的工程应变与真实应变。MTS仪器的数据采集速率与DIC的拍照速率保持一致。

图  4  数字图像相关测量系统(DIC)

Figure  4.  Digital image correlation measurement system (DIC)

下载: 全尺寸图片 幻灯片

2   试验结果和分析

2.1   断口特征

各温度工况下试件的断口形貌如图5所示，试件的峰值温度与拉伸温度会影响试件的断口特征，其断口外围轨迹与加载轴线的角度受温度的变化明显。在常温下，试件的断口为杯椎形，外围轨迹与轴线呈45°夹角，出现较为明显的颈缩现象。

图  5  试件断口形貌

Figure  5.  Fracture morphology of specimens

下载: 全尺寸图片 幻灯片

通过观察图5(a)~图5(c)可以发现，当试件处于升温状态时，拉伸温度对试件断口形貌的影响较为明显，随着温度的升高，试件的延性变好，断口表面剪切唇与拉伸方向的夹角逐渐增大，拉伸温度超过600 ℃时外围轨迹与加载轴线呈90°夹角，断口半径缩至很小。与常温下试件断口特征相比(图5(a))，降温段与高温后的试件断口表面(图5(d)~图5(f))没有发生明显的变化。这种现象可能是由两种因素造成的：一是高温后试件在常温下拉伸，峰值温度对试件断口形貌影响较小；二是由于试验条件的限制，降温段工况较少，试件在拉伸温度为200 ℃时，温度变化较小，试件的延性没有发生明显的变化。

缺口尺寸会影响试件的断口形貌。温度历程相同时，试件的缺口越小，即应力越集中，更容易出现外围轨迹与加载轴线呈90°夹角的现象。以升温段拉伸试件为例，如图5(h)和图5(n)所示，N3缺口圆棒试件在400 ℃时断口外围轨迹与加载轴线呈90°夹角，N6试件在400 ℃时断口外围轨迹与轴线仍呈45°夹角，只有在拉伸温度达到600 ℃时才会出现此类现象。

2.2   工程应力-应变曲线

传统拉伸试验过程中采用引伸计获取试件的工程应变，由于高温拉伸试验中试件变形较大，为获取全过程应变，需要在引伸计应变达到量程时手动暂停试验，对引伸计进行插拔处理。本试验采用DIC-3D系统获取试件的工程应变，为验证其准确度，在常温下采用两种方法同时进行试验，获取的工程应力-应变曲线对比如图6所示。可见，当试件处于弹性阶段时，误差较大，这是由于DIC-3D在测量微小应变时易受噪声影响；随着试件应变的增大，DIC结果与引伸计结果之间的相对误差逐渐缩小，验证了采用DIC-3D系统获取试件工程应力-应变曲线的有效性。

图  6  不同测量系统所得工程应力-应变曲线对比

Figure  6.  Comparison of engineering stress-strain curves measured by different measurement systems

下载: 全尺寸图片 幻灯片

2.2.1   升温段工程应力-应变曲线

升温段试件的应力-应变曲线如图7所示。对于光滑圆棒试件(图7(a))，钢材强度随温度升高呈现先升高后降低的变化趋势，延性呈现先降低后升高的趋势，这是由于在200 ℃~300 ℃时钢材发生蓝脆现象，强度略有提高，但塑性和韧性均降低。本文将工程应力-应变曲线下降段中曲线斜率突变点作为拉伸试件开始发生断裂的临界启裂点，将启裂点处的工程应变称为断裂标称应变，用断裂标称应变衡量试件的延性。

图  7  升温段不同试件的工程应力-应变曲线

Figure  7.  Engineering stress-strain curves of different specimens in heating stage

下载: 全尺寸图片 幻灯片

对于缺口圆棒试件(图7(b)和图7(c))，在相同温度下，应力三轴度会影响钢材力学性能对温度的敏感性。光滑圆棒在200 ℃时极限强度从常温的523 MPa增加至572 MPa，此时缺口圆棒的强度较常温没有发生明显变化，但延性的变化趋势仍然与光滑圆棒一致；随着温度的升高，缺口圆棒的延性随之升高。值得注意的是，应力三轴度越大，延性受温度的影响越小，在拉伸温度为400 ℃时，光滑圆棒、N6缺口圆棒、N3缺口圆棒的启裂点应变较常温分别增大37%、22%、17%；当拉伸温度升高至600 ℃时，三种试件的启裂点应变分别增大68%、32%、18%。

2.2.2   降温段工程应力-应变曲线

由图8可知，在降温段下，试件的极限强度受拉伸温度与峰值温度的影响，当构件的拉伸温度大于常温且相同时，峰值温度越高，试件的强度越低，延性越好；当拉伸温度为200 ℃且峰值温度为400 ℃时，光滑圆棒的极限强度为550 MPa，启裂点应变为0.3；峰值温度升至600 ℃时，光滑圆棒的极限强度降至524 MPa，启裂点应变增加至0.37。

图  8  降温段不同试件的工程应力-应变曲线

Figure  8.  Engineering stress-strain curves of different specimens in cooling stage

下载: 全尺寸图片 幻灯片

在降温阶段中，不同应力三轴度下，延性随温度变化的趋势相同，以拉伸温度200 ℃为例，光滑圆棒试件峰值温度为400 ℃时启裂点应变小于峰值温度为600 ℃试验值；对于不同缺口试件，峰值温度为400 ℃时N6缺口试件的启裂点应变与N3缺口试件的启裂点应变仍小于峰值温度为600 ℃取值。

2.2.3   高温后工程应力-应变曲线

如图9所示，当试件经历的峰值温度小于600 ℃时，峰值温度对高温后试件材性的影响较小，各试件的应力-应变曲线基本重合；当峰值温度超过600 ℃时，屈服强度与极限强度开始下降；当峰值温度达到800 ℃，屈服强度折减系数为0.87，极限强度折减系数为0.91。高温经历会增大钢材高温后延性，但变化幅度有限。随着峰值温度的升高(200 ℃~800 ℃)，钢材延性有逐渐降低的趋势。对于光滑圆棒试件，峰值温度为200 ℃时，延性最好(启裂点应变为0.54)，峰值温度为400 ℃、600 ℃、800 ℃时，启裂点应变分别为0.53、0.52、0.53，总体变化不明显；但对于缺口圆棒试件，峰值温度为800 ℃时，N6试件的延性降低至常温值，N3试件的延性略低于常温值(降低3%)。可见，高温后钢材在复杂应力下的延性可能低于常温设计值，导致高温后构件、结构的承载能力和变形能力不满足规范要求，有必要对高温后钢结构的残余极限承载力和残余极限变形进行评估和修正。

图  9  高温后不同试件的工程应力-应变曲线

Figure  9.  Engineering stress-strain curves of different specimens in post-fire stage

下载: 全尺寸图片 幻灯片

由图9可知，在高温后阶段，当试件经历相同的峰值温度时，应力三轴度对材性的影响较小。以峰值温度为800 ℃的试件为例，光滑圆棒、缺口N6试件和缺口N3试件的强度折减系数分别为0.85、0.87和0.89，而延性较常温没有发生明显变化。

2.3   材性折减系数与已有研究对比

国内外学者对火灾升温段和高温后结构钢材性进行了深入的研究，针对降温段材性研究较少，本文仅将Q355钢光滑圆棒试件升温段与高温后的弹性模量、屈服强度与已有研究结果进行比较。

对于升温段材性，通常采用稳态升温方法，即在恒定温度下进行拉伸试验，试验方法的差异性较小，通过与《建筑钢结构防火技术规范》^[17]、ANSI/AISC 360−2016^[15]、EN 1993-1-2: 2005^[14]、Q345冷成型钢高温试验结果^[27]对比(图10)。可见当拉伸温度小于600 ℃时，本试验获得的弹性模量折减系数介于国标与ANSI/AISC 360−2016^[15]曲线之间，在600 ℃时略高于ANSI/AISC 360−2016^[15]与EN 1993-1-2: 2005^[14]规范建议值；本试验屈服强度折减系数小于国标和ANSI/AISC 360−2016^[15]取值，与EN 1993-1-2: 2005^[14]结果较为相似，偏于安全。

图  10  升温段材性折减系数对比

Figure  10.  Comparison of reduction coefficient of material properties in heating stage

下载: 全尺寸图片 幻灯片

对于高温后材性，降温方法对材性影响较大，较常见的方法是自然冷却和水中冷却，本试验采用自然冷却方法，故比较高温后自然冷却下不同钢材受峰值温度的影响。通过与Q235^[28]、Q345^[29]、S460^[30]、Q460^[31]结果对比(图11)，发现在峰值温度低于800 ℃的范围内，高温后不同钢材弹性模量和屈服强度没有发生明显降低，折减范围在15%以内。总体上，本试验弹性模量折减系数低于其他钢材结果(偏安全)，与Q345试验结果^[29]相差较大(800 ℃时相差15%)，与Q460试验结果^[31]较为相似；本试验屈服强度折减系数在高温下(600 ℃以上)低于其他钢材结果(偏安全)。

图  11  高温后材性折减系数对比

Figure  11.  Comparison of reduction coefficient of material properties in post-fire stage

下载: 全尺寸图片 幻灯片

2.4   真实应力-应变曲线

在拉伸试验中，颈缩现象会导致试件横截面发生显著的变化，此时真实应力远大于工程应力，工程应力-应变曲线不能反映真实的材料拉伸应力状态和变形过程，有限元数值分析时需要输入材料的真实应力-应变曲线。常温拉伸试验中材料的真实应力-应变曲线常由标准拉伸试件(即光滑圆棒试件)的工程应力-应变曲线转化而成，本文采用常见的J2-Swift塑性本构模型^[32]确定试件的真实应力-应变曲线，颈缩前曲线通过式(1)确定：

式中：$\varepsilon$、$\sigma$分别为工程应变、工程应力；$\Delta l$为引伸计的伸长量；${l_0}$为试件的原始标距长度；F为荷载；${A_0}$为试件标距段内的初始横截面面积；${\varepsilon _{\rm{t}}}$、${\sigma _{\rm{t}}}$分别为真实应变、真实应力；$\overline \varepsilon$、$\overline \sigma$分别为等效应变、等效应力。

考虑到试件颈缩位置出现应力集中现象，试件由单轴受力状态变为复杂受力状态，式(2)不再适用描述试件颈缩后的真实应力-应变关系，本文采用如下Swift硬化准则确定颈缩后曲线：

式中：${\overline \varepsilon _{\rm{p}}}$为材料的等效塑性应变；K和n为材料的硬化参数。

本试验采用DIC-3D系统直接获得试件的真实应变与试件实时最小横截面半径，利用式(3)可以获得光滑圆棒的真实应力-应变关系。由于试件颈缩的影响，需要采用Bridgman公式^[33]对颈缩后的应力状态进行修正，如式(4)所示；由于在实际中颈缩面的曲率半径R难以测量，故采用LeRoy公式^[34](式(5))进行计算：

式中：r为试件任意时刻的最小横截面半径；${\sigma _{{\rm{cor}}}}$为修正后的应力结果；${\sigma _{\rm{t}}}$为未修正的初始真实应力；a为试件在某时刻颈缩面的半径；${\varepsilon _{\rm{t}}}$为试件未修正的初始真应变；${\varepsilon _{{\rm{p}},\max }}$为试件在极限荷载处的塑性真应变。

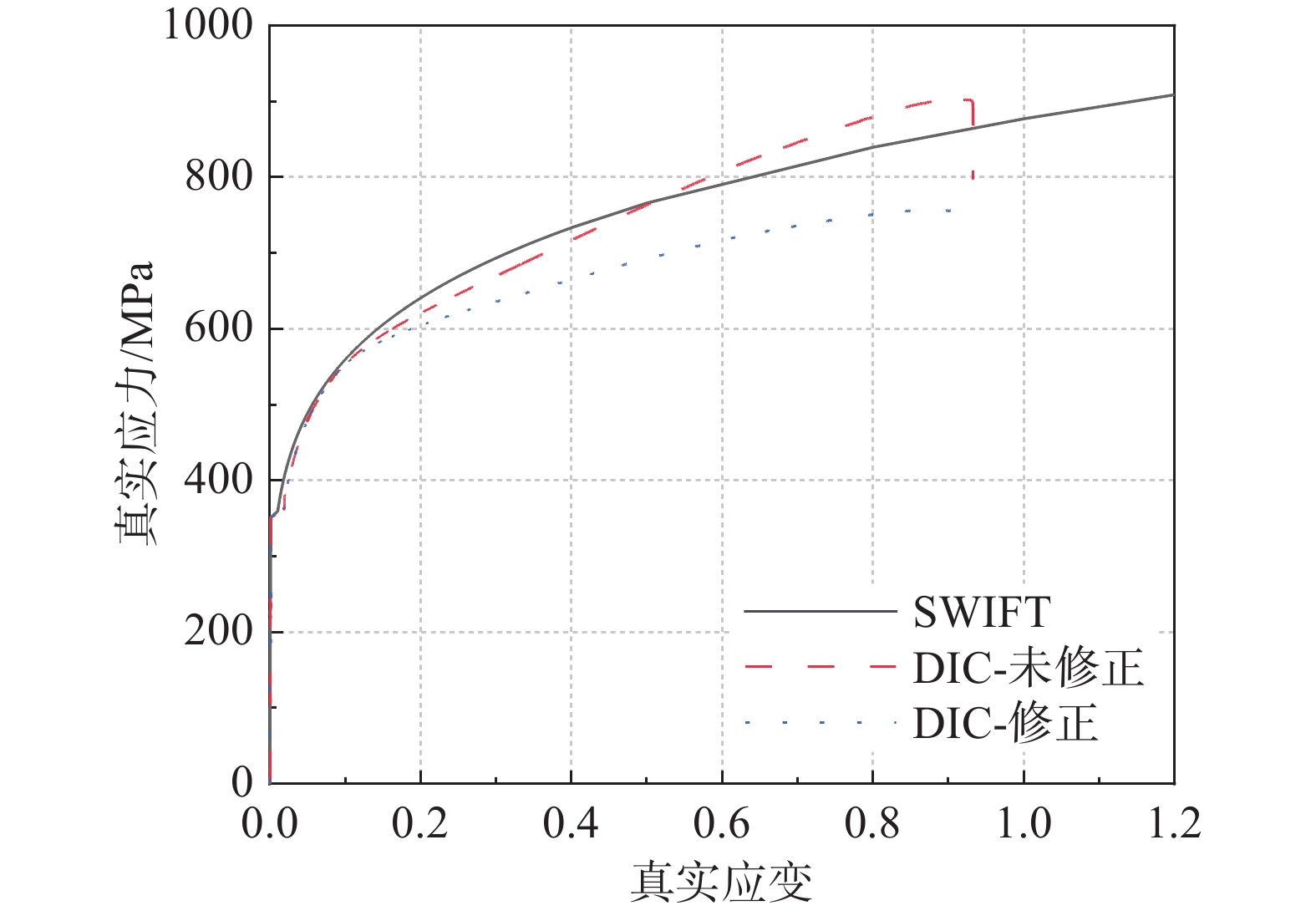
用上述两种方法(J2-Swift和DIC)计算常温下光滑圆棒的真实应力-应变曲线，如图12所示。两条真实应力-应力曲线在弹性阶段基本重合，修正后的最大真应力减小了9.9%，有效地消除了由于颈部横向应力对纵向应力的影响。

图  12  两种方法获得真实应力-应变曲线对比

Figure  12.  Comparison of true stress-strain curves obtained by the two methods

下载: 全尺寸图片 幻灯片

在升温段、降温段和高温后试验中，通过DIC量测光滑圆棒试件的真实应力-应变曲线，如图13所示。曲线对峰值温度与拉伸温度的敏感性不同，其中拉伸温度是影响真实应力-应变曲线的主要因素。在升温段(图13(a))，拉伸温度达到600 ℃时，真实应力在塑性阶段变化较为缓慢，这是由于钢材达到600 ℃时，延性变好导致材料的变形较为均匀，局部不会出现明显的剧烈收缩。由图13(b)可知，在降温段中，试件拉伸温度都为200 ℃时，峰值温度为400 ℃与600 ℃时试件的真实应力-应变曲线没有发生明显变化。高温后由于试件都在常温下拉伸(图13(c))，不同温度工况对真实应力-应变曲线影响很小。

图  13  基于DIC量测的光滑圆棒真实应力-应变曲线

Figure  13.  True stress-strain curves of smooth specimens obtained by DIC

下载: 全尺寸图片 幻灯片

有限元模拟时需要输入材料的真实应力-应变曲线，对于不同温度下的真实应力-应变曲线，常见做法是改变相应温度的屈服强度和极限强度，当试件发生颈缩后保持上升段斜率(真应力与真应变的比值)不变。该方法没有充分考虑不同温度下应变硬化行为对材料性能的影响。从图13可以看出，不同温度下真实应力-应变曲线的斜率不同，应变硬化行为在不同的温度历程下对构件和结构力学响应的影响不同。以升温段600 ℃为例(图13(a))，真实应力-应变曲线在塑性段近似为水平直线，斜率远小于常温下的真实应力-应变曲线。另外，真实应力-应变曲线不会一直发展下去，当试件发生断裂时中断，在使用真实应力-应变曲线时需要通过断裂准则定义真实的断裂点，具体见下一节介绍。

2.5   平均断裂应变

在多轴应力状态下，采用材料断裂前所承受的等效塑性应变来衡量钢材的延性，将断裂时刻的等效塑性应变称为断裂应变。本文利用BRIDGMAN^[33]提出的式(6)计算试件的断裂应变(即平均断裂应变)，启裂点应变和平均断裂应变都可以用于衡量钢材的延性，区别在于前者对应工程应变，而后者是真实应变，可输入到数值模型中。根据式(6)可知，平均断裂应变取值主要是由断面收缩率决定，各试件计算结果如表2和图14所示。

表  2  不同温度工况平均断裂应变较常温工况的折减系数

Table  2.  Reduction factor of average fracture strain

试件 编号	平均断裂 应变	折减 系数		试件 编号	平均断裂 应变	折减 系数		试件 编号	平均断裂 应变	折减 系数
SR	1.25	1.00		N6R	0.77	1.00		N3R	0.78	1.00
SH2	0.87	0.69		N6H2	0.63	0.82		N3H2	0.67	0.86
SH4	1.78	1.42		N6H4	1.26	1.64		N3H4	1.04	1.33
SH6	2.36	1.88		N6H6	1.42	1.84		N3H6	1.30	1.67
SC4-2	0.89	0.71		N6C4-2	0.66	0.86		N3C4-2	0.71	0.91
SC6-2	0.94	0.75		N6C6-2	0.68	0.89		N3C6-2	0.74	0.95
SC6-4	1.85	1.48		N6C6-4	1.12	1.45		N3C6-4	1.04	1.30
SA2	1.21	0.97		N6A2	0.75	0.97		N3A2	0.78	0.99
SA4	1.31	1.05		N6A4	0.78	1.01		N3A4	0.74	0.95
SA6	1.18	0.94		N6A6	0.83	1.08		N3A6	0.79	1.01
SA8	1.19	0.96		N6A8	0.81	1.05		N3A8	0.81	1.04

下载: 导出CSV 

| 显示表格

式中：${\overline \varepsilon _{\rm{f}}}$为平均断裂应变；${a_0}$为圆棒试件最小横截面的初始半径；${a_{\rm{f}}}$为圆棒试件断裂后最小横截面的半径。

在升温阶段中，钢材的平均断裂应变受拉伸温度的影响较大，当拉伸温度为200 ℃时，光滑圆棒的平均断裂应变减小至0.87，而后随着拉伸温度的增大，平均断裂应变逐渐增大(图14(a))，拉伸温度达到600 ℃时增加至2.36；在降温阶段，峰值温度对平均断裂应变的影响较小(图14(b))，拉伸温度为200 ℃时，峰值温度从400 ℃升至600 ℃时，平均断裂应变从0.89增加至0.94；高温后峰值温度对钢材平均断裂应变几乎没有影响(图14(c))。

在火灾全过程中，应力三轴度会改变试件断裂性能对温度的敏感性，如升温段拉伸温度为200 ℃时(表2)，光滑圆棒的断裂应变折减系数为0.69，随着应力三轴度增大，N6缺口试件与N3缺口试件的折减系数分别为0.82与0.86，随着峰值温度的增大，光滑圆棒试件断裂应变折减系数都远小于缺口试件。

图  14  试件平均断裂应变折减系数

Figure  14.  Reduction factors of average fracture strain of specimens

下载: 全尺寸图片 幻灯片

3   微观断裂机制分析

为了进一步研究复杂应力状态下Q355钢材微观断裂机制，对各温度工况下试件的断口表面进行电镜扫描分析，光滑圆棒试件纤维区的扫描结果如图15所示，断口表面都呈现出较为典型的“微孔型”断裂机制，断口的中心纤维区都出现了大量的等轴韧窝，说明试件破坏均属于韧性断裂。因此，本文所选用的SMCS韧性断裂模型适用于预测钢材火灾全过程的断裂行为(详见第4节)。

图  15  光滑圆棒试件典型的断口微观形貌

Figure  15.  Typical micro surface characteristics of smooth round specimens

下载: 全尺寸图片 幻灯片

由图15可知，当拉伸温度升高至600 ℃，断口表面韧窝尺寸变大，深度变深，材料性能改变；比较图15(a)和图15(b)，试件断口表面韧窝尺寸与深度没有发生明显变化，材料性能几乎没有发生改变；该现象与2.3节中升温段和高温后的材料性能折减系数的变化趋势相符合。

图16显示试件断口表面纤维区占比与拉伸温度和峰值温度有关；在升温段与降温段，随拉伸温度升高，纤维区占比越大，韧性越好，强度越低。在拉伸温度为400 ℃时，纤维区面积占比增大，延性变好。如图16(b)和图16(c)所示，拉伸温度相同时(400 ℃)，峰值温度600 ℃的韧窝深度大于峰值温度400 ℃时取值，即对于相同的拉伸温度，降温段试件的塑性变形能力大于升温段试件，这是由于在相同拉伸温度时，随峰值温度的增大，纤维区占比越大。高温后(图16(d))，相较于常温断口表面没有发生明显的变化。

图  16  温度对试件微观断裂形貌的影响

Figure  16.  Effect of temperatures on micro fracture characteristics of specimens

下载: 全尺寸图片 幻灯片

当试件所经历的温度历程相同时，断口表面特征与应力三轴度有关，如图17所示。应力三轴度越大，断口表面韧窝尺寸越小，深度越浅，光滑圆棒的延性好于缺口圆棒试件。

图  17  应力三轴度对试件微观断裂形貌的影响

Figure  17.  Effect of stress triaxiality on micro fracture characteristics of specimens

下载: 全尺寸图片 幻灯片

4   断裂模型参数标定及验证

4.1   断裂模型参数标定

断裂模型作为联系材料层次和结构层次的重要纽带，运用于数值分析时，需要对其进行参数标定。已有研究表明^[35-37]：在常温下高应力三轴度范围内，钢材断裂应变主要受应力三轴度影响，随着应力三轴度的增大，材料的断裂应变逐渐减小。通过对金属试件进行试验，获取所需要的力学指标，对所需模型进行标定，使其能准确的预测出材料的断裂点。

本文选用SMCS模型^[38]，定量表征火灾全过程下Q355钢材的高温断裂性能，如式(7)所示。

式中：${\varepsilon _{{\rm{p,c}}}}$为断裂应变；$\eta$为试件的等效应力三轴度；${C_1}$和${C_2}$为材料参数。

将不同温度工况下试件的应力三轴度和断裂应变代入式(7)，获得材料参数${C_1}$、${C_2}$，从而得到试件在高应力三轴度范围内的断裂轨迹，如表3和图18所示，试件经历的峰值温度与拉伸温度会影响材料参数${C_1}$和C₂(图18)。在高温后工况下，峰值温度对其影响较小，当拉伸温度达到200 ℃时，断裂轨迹整体下移，这是由于钢材在200 ℃~300 ℃范围内发生了蓝脆现象；当拉伸温度大于200 ℃后拉伸试件的延性随温度升高而变化，断裂应变也随之增大。不同应力三轴度下，试件断裂性能对温度的敏感性是不同的，由图18(a)所示，以拉伸温度600 ℃为例，$\eta = 0.38$时的断裂应变折减系数为1.48，而$\mathrm{\eta }=1.2$时断裂应变折减系数高达1.89。

表  3  各温度工况下断裂模型参数C₁和C₂

Table  3.  Parameters C₁ and C₂ of fracture models under various temperature conditions

工况	峰值温度/(℃)	拉伸温度/(℃)	C1	C2
常温	20	20	2.50	1.40
升温段	200	200	0.70	0.50
	400	400	3.60	1.65
	600	600	3.30	1.10
降温段	400	200	0.81	0.46
	600		1.20	0.80
	600	400	3.00	1.30
高温后	200	20	2.50	1.40
	400		2.50	1.40
	600		2.63	1.40
	800		2.75	1.40

下载: 导出CSV 

| 显示表格

图  18  各温度工况下Q355钢材断裂轨迹

Figure  18.  Fracture track of Q355 steels under various temperature conditions

下载: 全尺寸图片 幻灯片

4.2   断裂模型数值验证

在ABAQUS有限元软件中建立光滑圆棒和缺口圆棒的数值模型，如图19所示。采用C3D8R一阶减缩积分单元，断裂模型采用柔性损伤，将2.4节得到的真实应力-应变曲线和4.1节得到的断裂轨迹分别带入材料力学模型和柔性损伤模型中，加载直至断裂，使用ABAQUS/Standard求解器计算，并与试验结果进行对比。在数值模拟中，分别建立升温段、降温段和高温后的材料模型和断裂轨迹，通过跟踪温度历程，可以调取各自阶段的材料数据，从而模拟火灾全过程下的结构力学性能。

图  19  圆棒试件有限元模型

Figure  19.  Finite element models of the specimens

下载: 全尺寸图片 幻灯片

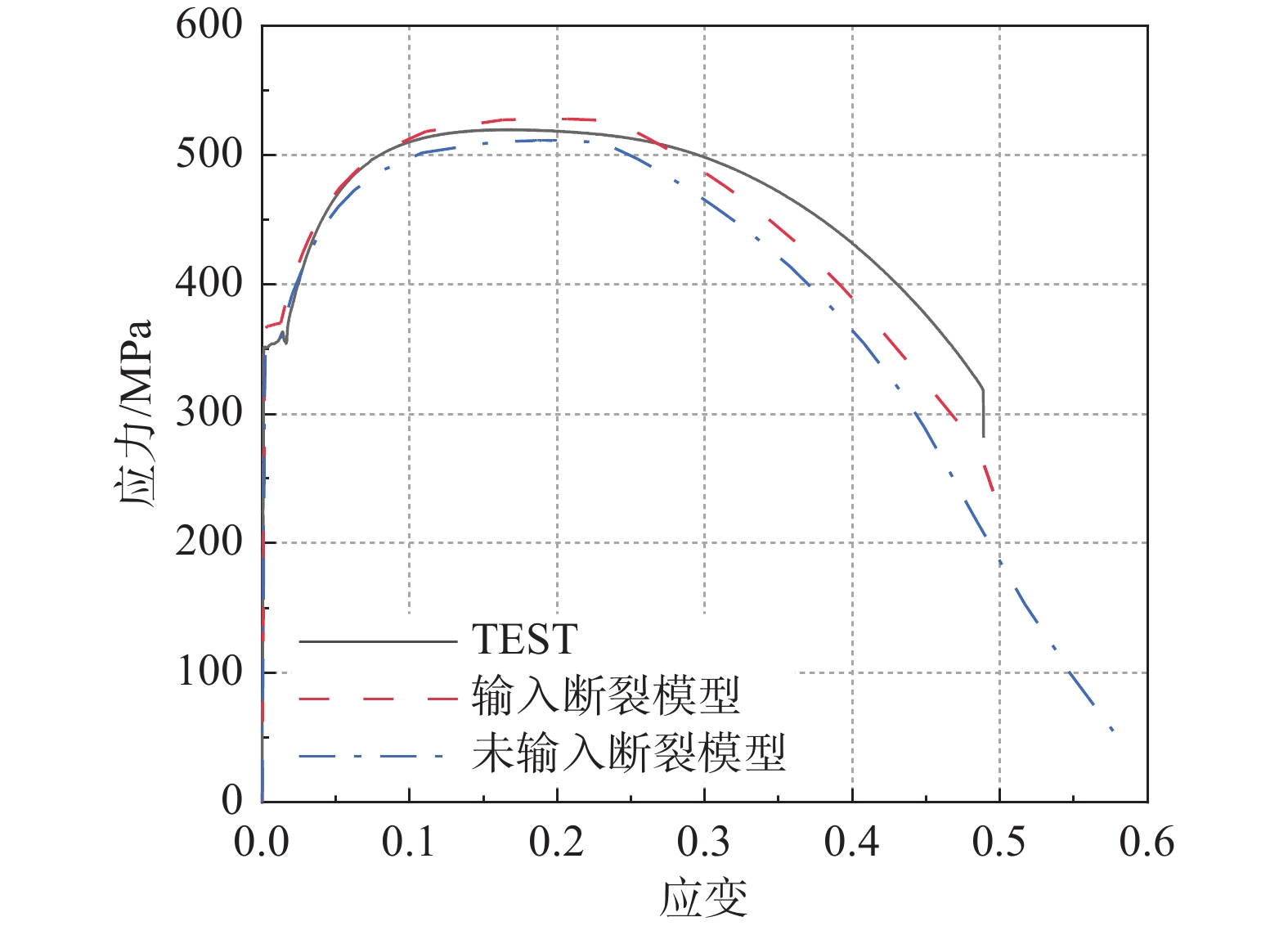
对于光滑圆棒常温断裂试验，采用断裂模型、未采用断裂模型的计算结果与试验结果对比如图20所示，可以发现通过此次拉伸试验所校准的断裂模型能够准确的预测试件的断裂位置，误差在5%以内。

图  20  光滑圆棒试件有限元计算结果

Figure  20.  Finite element calculation results of smooth specimens

下载: 全尺寸图片 幻灯片

比较常温下光滑圆棒试件断口位置的试验结果和模拟结果，如图21所示，SMCS断裂模型能准确地预测试件的断口位置，模拟结果的断口位于试件上部，与试验结果较为吻合。

图  21  光滑圆棒试件断口结果比较

Figure  21.  Comparison of fracture results of smooth round bar specimens

下载: 全尺寸图片 幻灯片

升温段、降温段和高温后光滑圆棒和缺口圆棒试件的工程应力-应变曲线数值模拟和试验结果对比如图22所示，有限元所预测的断裂位置与实际试件的断裂位置较为接近，误差在10%以内，说明SMCS模型适用于预测高应力三轴度范围下火灾全过程中Q355钢的断裂行为，应力三轴度的改变不会影响SMCS断裂模型的准确性。而在升温段拉伸温度为600 ℃时(图22(a))，数值分析得到的应力值在下降段明显小于试验值，这是由于下降段的软化在数值模型中更为明显，此现象对断裂点的预测没有明显的影响。

图  22  试件工程应力-应变曲线数值模拟和试验结果对比

Figure  22.  Comparison between numerical simulation and experimental results of engineering stress-strain curves of specimens

下载: 全尺寸图片 幻灯片

5   结论

本文对Q355钢材火灾升温段、降温段以及高温后的断裂性能进行了试验研究，得到了不同应力状态和温度下的真实应力-应变曲线、断裂应变，并结合数值模拟对断裂模型进行参数标定，主要结论如下：

(1) 材料高温断裂性能与所经历的峰值温度和拉伸温度有关，拉伸温度为主要影响因素；当拉伸温度大于200 ℃时，峰值温度才会影响断裂性能，峰值温度越高，断裂延性越好；高温后断裂性能较常温情况无明显变化。

(2) 应力三轴度会影响材料断裂性能对温度的敏感性，升温阶段影响尤为明显，应力三轴度越大，材料平均断裂应变折减系数变化越小。

(3) 火灾全过程中钢材均具有韧性断裂特征，拉伸温度与峰值温度越高，纤维区占比越大，韧窝平均直径越大。随着应力三轴度的增大，纤维区占比逐渐减小。

(4) SMCS断裂模型能准确预测火灾过程中高应力三轴度下Q355钢的断裂行为，在不同温度工况下材料参数会随温度历程而发生变化。